一种单自由度振动系统动态载荷识别方法

武江凯，白明生，张 永（中国空间技术研究院 载人航天总体部，北京 100094）



一种单自由度振动系统动态载荷识别方法

武江凯，白明生，张 永
（中国空间技术研究院 载人航天总体部，北京 100094）

摘要：航天器在飞行过程中经历了复杂的力学环境，但是目前又无法直接测量出这种复杂力学载荷函数。针对这一问题，提出了一种应用力学载荷识别方法确定航天器所经受力学载荷的新方法，针对单自由度振动系统模型，以二次多项式为基函数，推导建立了基于Duhamel积分的动态载荷识别模型。仿真分析结果表明，该方法具有很高的识别精度，且不存在误差积累问题。该方法为下一步试验验证和工程应用提供了理论基础和技术支撑。

关键词：复杂力学环境；载荷识别；Duhamel积分；二次多项式

http://www.bisee.ac.cnE-mail:htqhjgc@126.comTel:(010)68116407, 68116408, 68116544

0　引言

确定载荷的方法一般有两种，即直接测量法与间接识别法。前者直接测量载荷本身或通过测量与载荷有关的参数确定载荷的大小。比如，为了给国际空间站开展微重力环境研究做准备，NASA曾在“和平号”空间站对航天员在舱内行走所引起的载荷进行了测量。然而在工程实际中，由于结构和载荷本身的复杂性（如运载火箭在飞行中产生的震颤、海洋平台等大型构筑物受风浪、基础激励作用等），很难对作用于结构的外载荷特别是冲击载荷进行直接测量或计算。因此，由结构的动响应和结构的动态特性来间接反演动载荷是非常必要的。

载荷识别起源于20 世纪70 年代末，因研究直升机飞行时螺旋桨主轴所受到的力等军事用途而得以发展[1-2]。到目前为止，动态载荷识别方法主要有频域法和时域法。频域法提出较早、发展成熟且识别精度高，其缺点是在结构固有频率处求解方程容易出现病态，对响应信号样本有一定长度要求，对噪声影响也非常敏感，只适用于稳态动载荷和随机载荷的识别[3-4]。时域法对各种载荷识别都具有较强优势，但目前该方法大都基于待识别载荷为一阶跃载荷或Wilson-θ假设，通过建立递推连锁计算格式进行求解，但对采样时间和初值都很敏感，存在累积误差[5-8]。近年还发展了计权加速度法（SWAT）、逆系统求解法、基于神经网络法、小波变换法等[9-10]，但都处于载荷识别初步研究阶段。

本文提出一种基于单自由度振动系统的动态载荷识别方法：以二次多项式为基函数，建立基于Duhamel积分的单自由度振动系统的载荷识别模型，并通过仿真分析对模型的正确性进行验证。

1　单自由度振动系统描述

典型单自由度振动系统如图1所示。

图1　单自由度振动系统Fig. 1　Single-degree-of-freedom vibration system

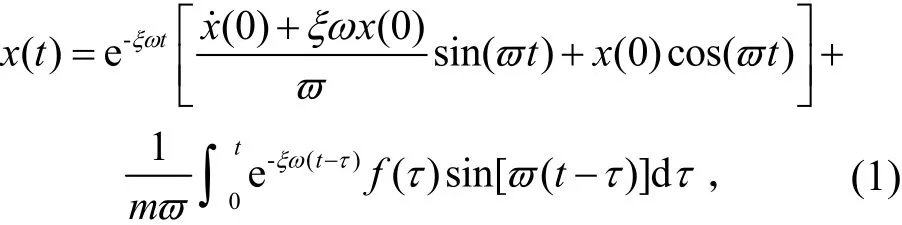
式中：x&&、x&、x分别为单自由度振动系统加速度、速度和位移信号；m、c、k分别为振动系统的质量、阻尼和刚度；为自振角频率；为阻尼比；；x(0)、x&(0)为初始位移和初始速度；f(τ)为待识别的动态载荷[13]。

2　单自由度振动系统载荷识别方法

动态载荷识别问题，其实就是通过以上3个方程组联立求解f(τ)的问题。由于该求解问题是一个非线性的非正定问题，对应f(τ)为一个解集，所以本文选择二次函数f(t)=at2+bt+c作为f(τ)的基本形式，将动态载荷f(τ)的求解问题转换为求取不同时刻参数a、b、c的问题。

动态响应的测试信号可以是动态位移、动态速度或者动态加速度等，在ti-1时刻的响应xi-1反映了在初始条件和此刻以前动态载荷综合作用下的结果。为了减小累积误差和消除对初始条件的敏感性，在对某一时刻动态载荷识别时，可在[ti-1, ti+1]时间段内进行，以ti-1时刻的响应为初值，即在[ti-1, ti+1]时间段内设ti-1为0时刻，由于在ti-1、ti、ti+1时刻的函数值中，ti时刻的精度最高，所以在[ti-1, ti+1]时间段内仅作fi的识别。

以ti-1时刻为初值，利用Duhamel积分求解得到ti时刻的响应为：

将载荷函数f(t)=at2+bt+c代入式(4)，则式(4)中的积分项可写为

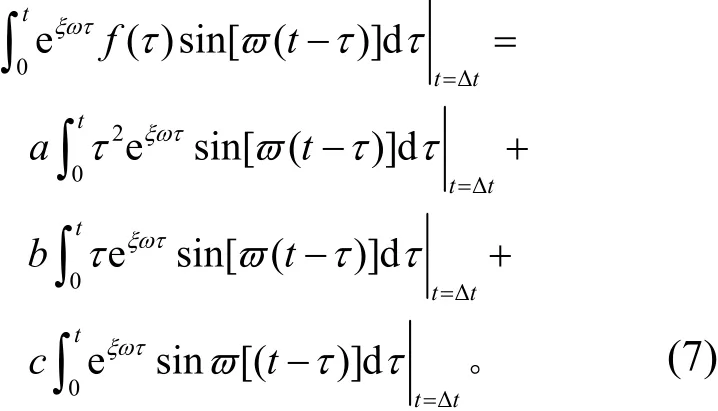
同理也可以将载荷函数代入式(5)、式(6)中的Duhamel积分项，然后对Duhamel积分参数Iu2、Iu1、Iu0、Iv2、Iv1、Iv0、Iw2、Iw1、Iw0进行如下设定：

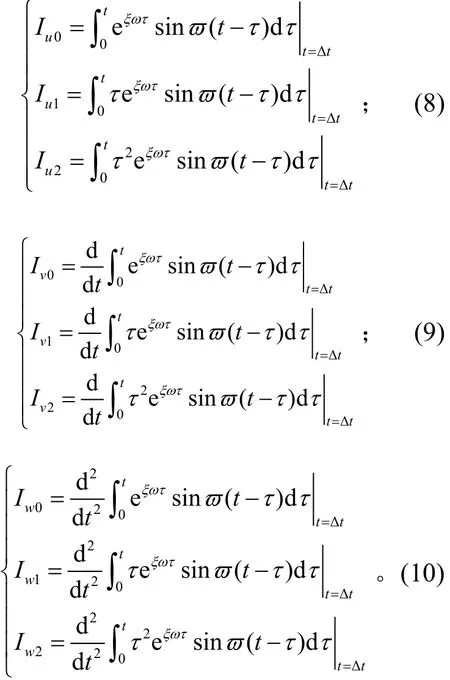
式(8)～式(10)中都有显式结果，限于篇幅，在此处不一一列出。分别将式(8)、式(9)和式(10)代入到式(4)、式(5)和式(6)，则有：

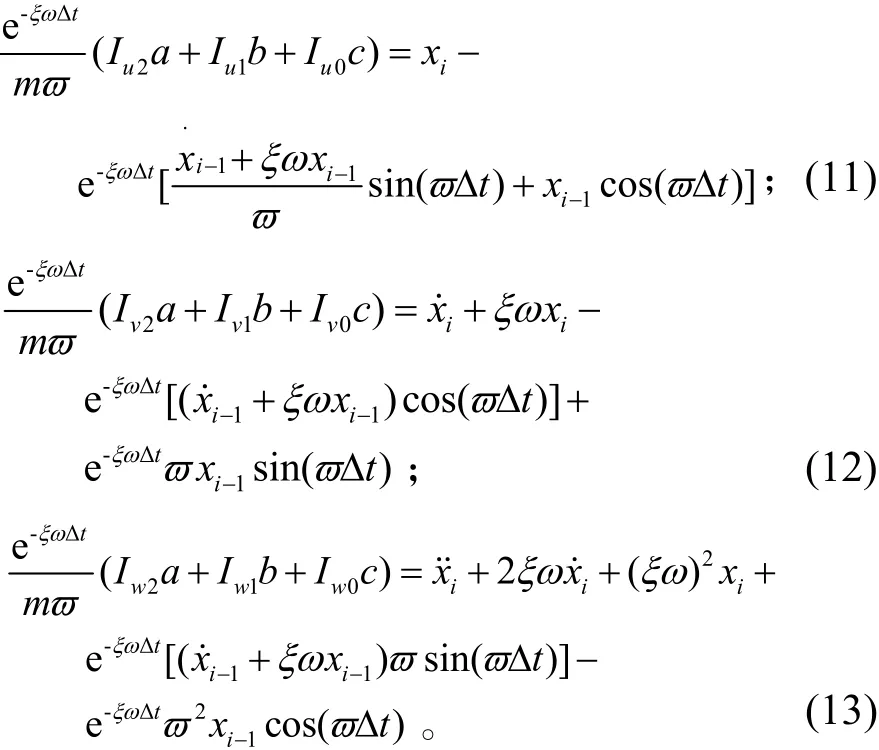
式(11)～式(13)的右端项可由ti时刻和ti-1时刻的系统位移、速度和加速度相应得到。分别令式(11)～式(13)的右端项为qi、q&i、q&i&，则可得到

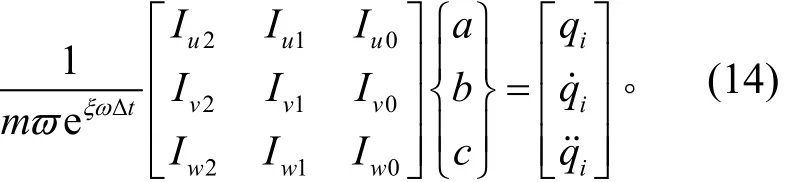
同理，分别对ti+1时刻的Duhamel积分参数Iu21、Iu11、Iu01、Iv21、Iv11、Iv01、Iw21、Iw11、Iw01进行设定，则通过对动力响应方程进行变形、简化，可得

通过方程推导，将载荷识别转化为式(15)中对{α}的求解问题。由于在信号测试中存在测量误差和噪声，所采用的动态载荷拟合函数与实际的动态载荷存在差异，所以，式(15)为矛盾方程组。对于矛盾方程组的求解，本文选择构造误差e的方程：

于是将满足式(15)的求解问题转化为求eTe极小值，进而转化成求解式(16)最小二乘解[14]，即：

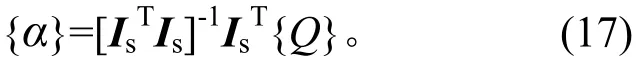
在待定参数a、b、c求得后，则可将[ti-1, ti+1]时间段内的动态载荷描述按f(t)=at2+bt+c的形式给出。但依据Gauss插值的性质，以中间点的插值精度最高，因此，在[ti-1, ti+1]时间段，取ti时刻的值为识别结果，即fi= a∆t2+b∆t+c，然后后移一个∆t的时间间隔作下一个时刻的动态载荷识别。

3　算例仿真分析

为了验证单自由度振动系统动态载荷识别理论的正确性，本文采用图1所示系统对识别方法进行仿真验证。

为不失一般性，设系统中m=1 kg；c=0.4 N·s/m；k=1 N/s；f(t)=F0sin(ωt)，F0=1 N，ω=5 rad/s，t∈[0, 20] s，分析步长Δt取为0.1 s，得到原始载荷时间历程f(t)，如图2所示。

图2　原始载荷时间历程Fig. 2　Time history of original load

依据结构动力学理论，应用Duhamel积分，单自由度系统在外界激振力作用下系统位移、速度和加速度响应如图3所示。

图3　激振力作用下单自由度系统响应Fig. 3　Response of single-degree-of-freedom system with excitation force

应用本文研究的动载荷识别理论及测得的系统响应值对外加激励载荷进行识别，识别结果及相对误差分别如图4和图5所示。

图4　识别载荷时间历程Fig. 4　Time history of load identification

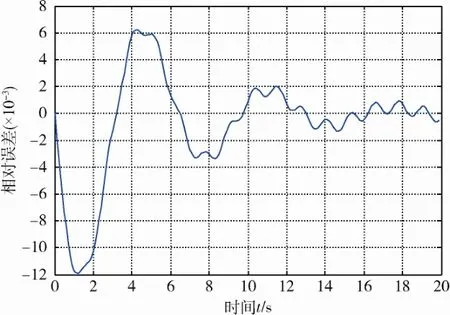
图5　识别载荷误差曲线（步长0.1 s）Fig. 5　Error curve of load identification(time step is 0.1 s)

从图5可以看出：动态载荷识别稳定误差不超过2%，且只与求解时刻及其前后时刻的振动状态有关，而不受此前时刻载荷的影响，同时也不会对以后识别产生影响；识别过程不受初值和边值的影响，不会带来误差传递和累积问题，即误差不会出现扩散；识别结果都能很好地逼近原始输入载荷，最小误差稳定在2‰之内，说明本识别方法对测量干扰具有较强的鲁棒性。

保持系统参数不变，调整分析步长Δt为0.01s情况下的系统识别误差如图6所示。可看出，识别精度提高了1个数量级，即系统识别精度会随着采样频率的提高而提高，说明提高采样频率对改善载荷识别精度具有重要作用。

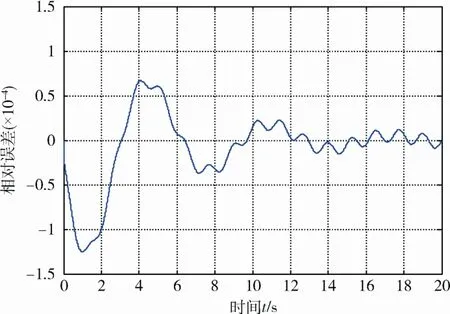
图6　识别载荷误差曲线（步长0.01s）Fig. 6　Error curve of load identification(time step is 0.01 s)

4　结束语

本文以二次多项式为基函数，基于Duhamel积分和模态分解技术推导建立了单自由度振动系统载荷识别模型，可对各种非平稳动态载荷进行实时识别，同时对样本数据长度没有要求；由于不进行傅里叶变换，避免了由截断带来的窗泄漏问题。算例仿真结果表明：该识别方法具有很高的识别精度，且不存在误差传递和积累问题；提高采样频率对提高系统的识别精度有重要作用。

鉴于该方法的理论推导及仿真分析仅针对单自由度振动系统，且有待进一步试验验证，以及在复杂多自由度动态载荷识别方面还存在不确定性及局限性，因此在后续工作中有待深入研究。

参考文献（References）

[1] Schulte H, Gerland P. A systematic load identification procedure for parallel robot manipulators[C]∥Mechanics of 21stCentury ICTAM04 Proceedings. Warsaw, Poland, 2004: 21-22

[2] Nordstrom L J L. A dynamic programming algorithm for input estimation on linear time-variant system[J]. Comput Method Appl Mech Engrg, 2006, 195: 6407-6427

[3] 胡寅寅, 率志君. 设备载荷识别与激励源特性的研究现状[J]. 噪声与振动控制, 2011, 31(4): 1-5 Hu Yinyin, Shuai Zhijun. Status of study on machine’s load identification technique[J]. Noise and Vibration Control, 2011, 31(4): 1-5

[4] 智浩, 文祥荣, 缪龙秀, 等. 动态载荷的频域识别方法[J].北方交通大学学报, 2000, 24(4): 5-10 Zhi Hao, Wen Xiangrong, Miao Longxiu, et al. Dynamic loading identification in frequency domain[J]. Journal of Northern Jiaotong University, 2000, 24(4): 5-10

[5] 赵凤遥, 张运良, 马震岳. 动载荷的时域识别方法及其应用[J]. 水电能源科学, 2005, 23(1): 8-11 Zhao Fengyao, Zhang Yunliang, Ma Zhenyue. Method and application of dynamic load identification in time domain[J]. Water Resources and Power, 2005, 23(1): 8-11

[6] 朱斯岩, 朱礼文. 运载火箭动态载荷识别研究[J]. 振动工程学报, 2008, 21(2): 135-139 Zhu Siyan, Zhu Liwen. Dynamic load identification on launch vehicle[J]. Journal of Vibration Engineering, 2008, 21(2): 135-139

[7] Allen M S, Carne T G. Delayed, multi-step inverse structural filter for robust force identification[J]. Mechanical Systems and Signal Processing, 2008, 22(5): 1036-1054

[8] 徐菁, 张方, 姜金辉, 等. 运用数值迭代的动载荷识别算法[J]. 振动工程学报, 2014, 27(5): 702-707 Xu Jing, Zhang Fang, Jiang Jinhui, et al. An algorithm of dynamic load identification based on numerical iteration[J]. Journal of Vibration Engineering, 2014, 27(5): 702-707

[9] 马庆镇. 推力终止时结构的载荷识别及瞬态响应分析[D].长沙: 湖南大学, 2014: 7-11

[10] 王慧儒, 谢晓竹, 吴淼. 基于逆传系统法的动态载荷识别研究[J]. 装甲兵工程学院学报, 2005, 19(3): 79-82 Wang Huiru, Xie Xiaozhu, Wu Miao. Study on the dynamic load identification based on inversion system method[J]. Journal of Academy of Armored Force Engineering, 2005, 19(3): 79-82

[11]Doyle J F. A wavelet deconvolution method for impact force identification[J]. Experimental Mechanics, 1997, 37(4): 403-408

[12]邱吉宝, 向树红, 张正平. 计算结构动力学[M]. 合肥: 中国科学技术大学出版社, 2009: 316-323

[13]陈祖明, 周家胜. 矩阵论引论[M]. 北京: 北京航空航天大学出版社, 1998: 175-194

（编辑：许京媛）

The danamic load identification for a single-degree-of-freedom vibration system

Wu Jiangkai, Bai Mingsheng, Zhang Yong
(Institute of Manned Space System Engineering, China Academy of Space Technology, Beijing 100094, China)

Abstract:The spacecraft is in a complicated mechanical environment, and its external load can not be measured directly. So a mechanical load identification method is proposed for spacecraft during the flight phase. Based on the Duhamel’s integration, with the second order polynomial as the base function, the dynamic load identification mode for a single-degree-of-freedom vibration system is built. The simulation results show that this method has a high identification precision and the problem of error accumulation is solved. The method can provide theoretical bases and technological supports for the test validation and engineering applications.

Key words:complicated mechanical environment; load identification; Duhamel’s integration; quadratic polynomial

作者简介：武江凯（1987—），男，从事航天器总体设计工作。E-mail：wjk1958@126.com。

基金项目：国家重大科技专项工程

收稿日期：2015-08-17；修回日期：2016-03-04

DOI:10.3969/j.issn.1673-1379.2016.02.004

中图分类号：V416.2

文献标志码：A

文章编号：1673-1379(2016)02-0136-05