自并励静止励磁系统精细建模及仿真
董久晨,王西田,刘明行,章晨翔
(1.上海交通大学 电力传输与功率变换控制教育部重点实验室,上海 200240;2.上海电气电站设备有限公司发电机厂,上海 200240)
0 引言
励磁系统的基本功能是给发电机的励磁绕组提供合适的直流电流,以在发电机定子空间产生磁场,实现控制和保护功能[1]。准确建立励磁模型对于电力系统稳定研究十分重要[2-5]。目前,用于电力系统稳定研究的国内外励磁模型标准[6-7],简化了功率单元和励磁电源。然而,对于电力系统应用广泛的自并励静止励磁系统,其电源取自机端电压,近机端的接地故障将会直接影响励磁电压,在近机端发生接地故障时,采用传递函数的静止励磁系统模型将不能满足准确分析暂态稳定问题的研究需求。并且,采用传递函数的模型忽略了功率整流单元的非线性过程,使得在暂态过程对励磁系统动态性能的分析可能缺乏准确性。
文献[8]计算比较自并励静止励磁和高起始无刷励磁系统对暂态稳定的影响,得出无刷励磁暂态稳定性能优越的结论。然而上述文献并未对自并励静止励磁系统的功率单元和励磁电源进行精细建模,对静止励磁系统的分析结果可能缺乏准确性。因此,在电力系统暂态稳定问题研究中,对静止励磁系统的功率单元和励磁电源精细建模十分必要。
灭磁系统的作用是当发电机内部及机端发生诸如短路及接地等事故时迅速切断发电机的励磁,并将储存在励磁绕组中的磁场能量快速消耗在灭磁回路[9]。灭磁系统的建模仿真是研究灭磁特性的有效手段。然而,目前对用于电力系统稳定研究的励磁系统模型中建立灭磁模型的研究尚未见诸报道。
为满足电力系统暂态稳定以及励磁装置特性研究的需要,本文考虑功率单元和励磁电源以及灭磁系统的特性,建立自并励静止励磁系统的精细模型,并利用PSCAD/EMTDC建立励磁系统精细模型的电磁暂态仿真模型,对近机端接地故障后的暂态稳定和励磁装置特性进行详细仿真分析。
1 静止励磁系统精细模型
自并励静止励磁系统框图如图1所示,本文对励磁电源和功率整流桥的电路进行建模,并在功率整流桥中加入灭磁系统。
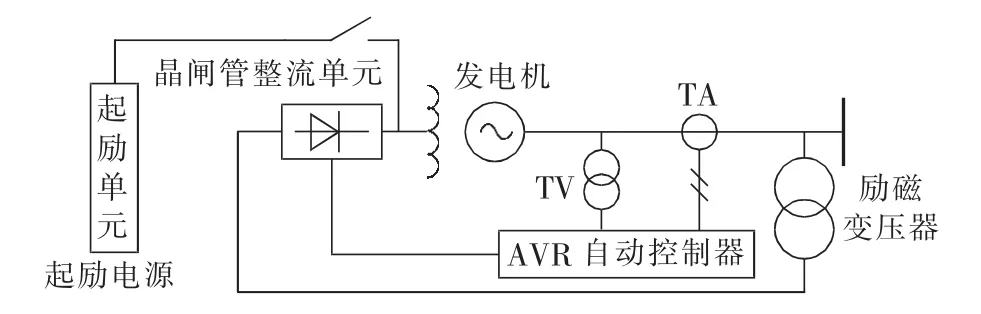
图1 自并励静止励磁系统Fig.1 Bus-fed static excitation system
完整的励磁系统模型框图如图2所示,电压偏差信号经过AVR自动控制器得到AVR励磁电压信号EAVR,再由触发角控制器生成整流器触发角信号α,整流桥将励磁变压器二次侧电压整流得到励磁直流电压 Ef,其平均值如式(1)所示。
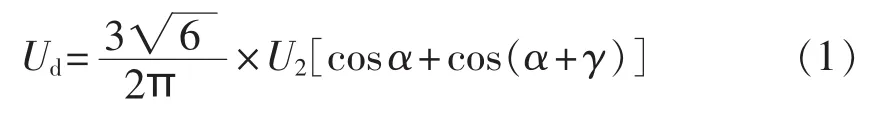
其中,Ud为励磁直流电压Ef的平均值;U2为励磁变压器二次侧相电压有效值;α为触发角;γ为换相角。
常规的励磁系统模型简化了功率单元和励磁电源,即图2中的移相触发和可控整流框图。在静态稳定或对励磁电源影响不大的暂态稳定研究中,在标幺单位制下可认为:

图2 励磁系统模型框图Fig.2 Block diagram of excitation system model
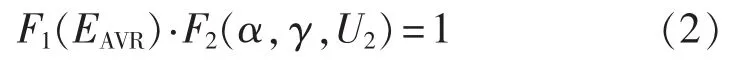
其中,F1、F2代表非线性的以及动态的映射关系,F1为移相触发算法特性,F2为式(1)的标幺化关系特性。此时,AVR励磁电压信号EAVR与励磁直流电压Ef等价,AVR励磁电压信号EAVR即可直接代替励磁系统模型励磁电压的输出。
将图2中功率单元和励磁电源展开,并引入灭磁回路,得到励磁系统整流功率单元结构框图,如图3所示。图3中的励磁电源取自机端电压,经过励磁变压器由可控整流桥整流后送入发电机励磁电路回路,电压偏差信号经过AVR和触发角控制器得到整流桥触发角信号α。灭磁回路中,R1和R2为氧化锌非线性电阻,S1和S2为分级灭磁控制开关。
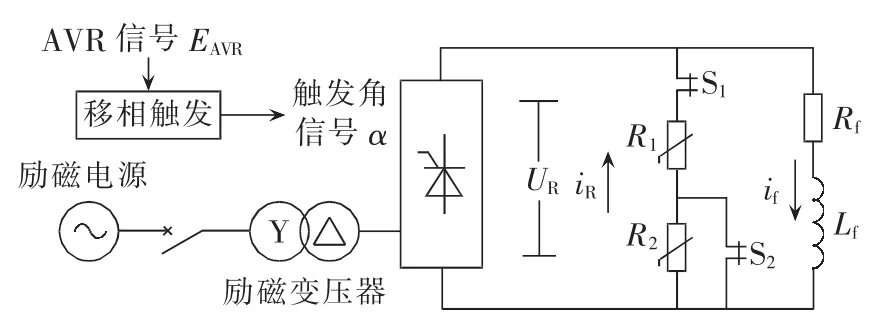
图3 励磁系统可控整流功率单元结构框图Fig.3 Structural diagram of controllable rectifier of excitation system
常见的灭磁方式有线性电阻灭磁、非线性电阻灭磁和逆变灭磁[10-11]。线性电阻和非线性电阻灭磁过程中,励磁回路电压方程为式(3),可求得灭磁过程中的励磁电流为式(4)。

其中,Lf和Rf分别为励磁回路电感和电阻;if为励磁电流;C为R1和R2的等效非线性电阻位形系数;β为非线性电阻系数(在线性电阻灭磁时,C为R1和R2的等效电阻阻值R,β为1);If0为灭磁前初始励磁电流值;T′d0为直轴开路瞬变时间常数。
逆变灭磁过程中,根据工程需要,将整流桥的触发角信号调至120°~150°,使得整流桥处于逆变状态,励磁电压反向,将能量回馈给电网,励磁电流迅速减小,从而达到灭磁效果。
为了准确研究电力系统暂态稳定以及励磁装置特性,本文提出的自并励静止励磁系统精细模型的整流功率单元需建立电磁暂态模型,可以利用电磁暂态程序实现[12]。
2 精细模型在PSCAD中的实现
本文基于PSCAD搭建了自并励励磁系统精细模型的电磁暂态模型。电磁暂态模型分为两部分:一部分是以IEEE中ST5B型传递函数模型为基础的AVR控制器部分[13-14];另一部分为用电路元件搭建的功率整流单元。这两部分都可以采用模型库中基本控制元件和电路元件实现。其中,AVR控制器部分利用插值法模拟移相触发的环节,输出一个触发角信号,用来对功率整流单元进行触发控制;功率整流单元根据触发角的调节,将励磁变二次电压整流后直接输出作为励磁电压。
PSCAD库中的励磁系统模型都为传递函数模型,发电机模型的励磁电压为信号端口。而精细模型中研究建立的励磁功率单元模型,在其直流侧与发电机励磁绕组构成一个闭合电路,模型库中的发电机模型不能满足研究需求,为此专门请PSCAD开发商提供了一个与励磁系统模型的接口是2个电路端口的同步发电机模型,如图4所示。利用此发电机模型与自并励励磁系统精细模型相配合,完成电磁暂态模型的仿真分析研究。
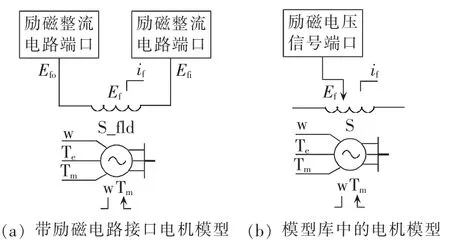
图4 PSCAD中与励磁系统模型接口的同步电机模型Fig.4 Synchronous machine model connecting with excitation system model in PSCAD
3 算例仿真
本文采用单机-无穷大母线系统,如图5所示,利用文献[15]中例4.1的典型电机模型参数,在PSCAD中对功率单元的灭磁功能进行了仿真验证,并通过改变机端故障持续时间和过渡电阻,对比分析传递函数模型和精细模型对电力系统暂态稳定的影响。
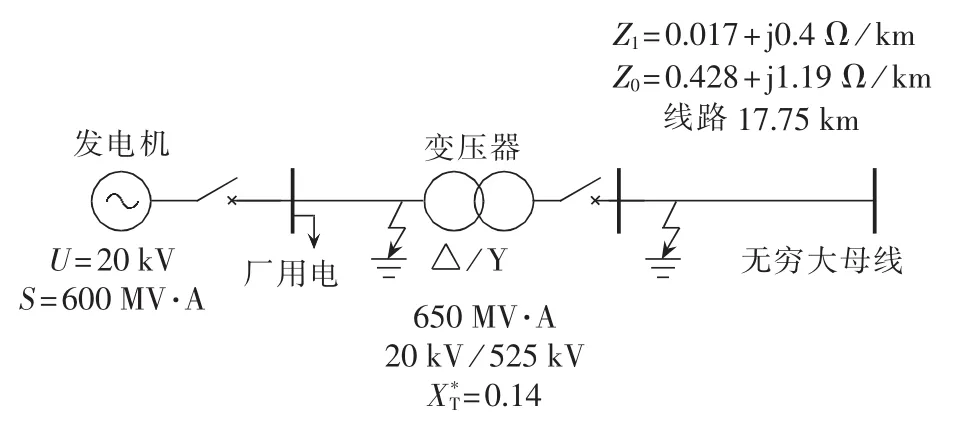
图5 单机-无穷大母线系统Fig.5 One-machine infinite-bus system
3.1 灭磁功能仿真
在发电机出口发生故障后,采用逆变和分级串入线性电阻联合灭磁方式进行灭磁。由图6可以看出,0.2 s时刻投入灭磁回路,AVR控制器控制触发角为120°,使得整流桥处于逆变状态,此时励磁电压为负,逆变灭磁起主要作用,使得励磁电流迅速减小;0.4 s之后分级线性电阻起主要作用,快速释放能量,到0.678 s时励磁电流降低为额定值的10%。

图6 灭磁功能仿真曲线Fig.6 Simulative curves of field suppression
3.2 暂态稳定对比仿真分析
在发电机出口位置设置不同严重程度的接地故障,故障工况如表1所示,对采用自并励静止励磁系统传递函数模型和精细模型的暂态稳定性进行比较分析,仿真结果见图7(机端电压Ut为标幺值)。

表1 不同严重故障工况Table 1 Simulation faults with different seriousness levels
从图7中可以看出,接地故障程度越严重对励磁电源的影响越大。励磁电源通过整流桥直接影响励磁电压,从而在机端电压中进行反馈;当故障程度较为严重时,诸如金属性三相接地故障,机端电压的跌落较大,直接影响励磁电源,采用精细模型励磁电压的强励倍数比采用传递函数模型的强励倍数要小得多,并且采用精细模型励磁电压强励的响应时间较长。其中PowR001T02工况的仿真曲线比文献[8]中的结果更接近实际故障过程。
在不同故障位置的三相接地故障,如表2所示,对采用自并励静止励磁系统传递函数模型和精细模型的暂态稳定性进行比较分析,仿真结果如图8所示(机端电压Ut为标幺值)。
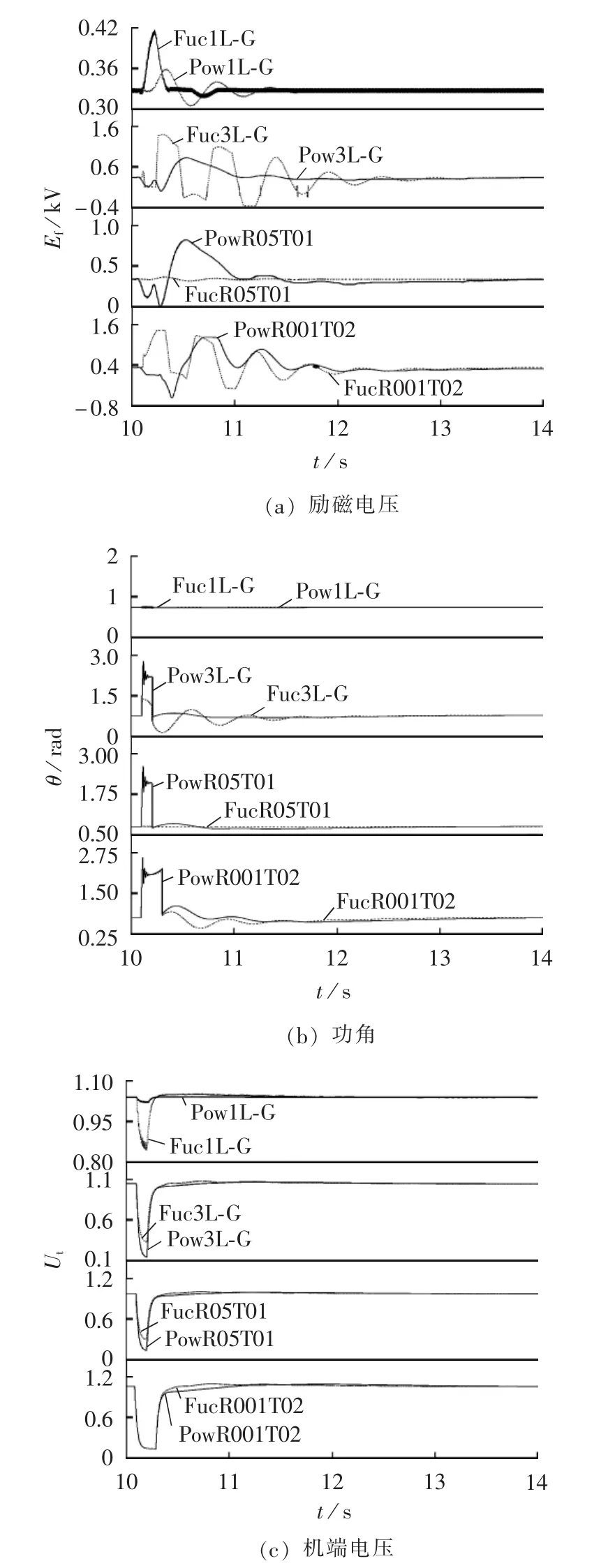
图7 不同严重故障下传递函数模型与精细模型仿真曲线Fig.7 Simulative curves by transfer function model and precise model for different serious faults
由图8可以看出,在主变高压侧的故障,故障程度较为严重时也会引起机端电压跌落,影响励磁电源。由于采用精细模型和传递函数模型的电压跌落暂态特性基本一致,因此2种模型的励磁电压仿真曲线较为接近。相比近机端故障,主变高压侧的故障过程中,2种模型励磁电压的强励效果较为明显,响应速度更快。
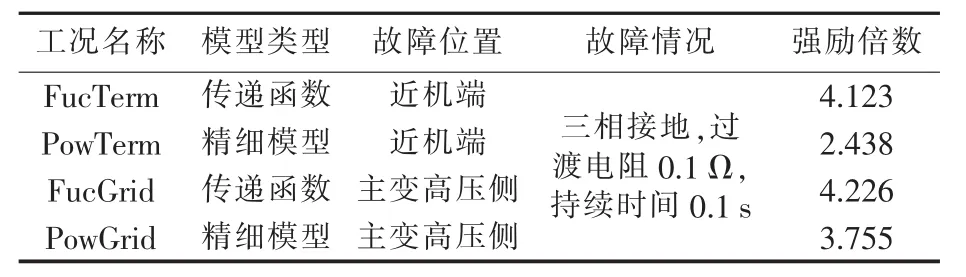
表2 不同故障位置接地故障工况Table 2 Simulation faults with different grounding fault locations

图8 不同故障位置传递函数模型与精细模型仿真曲线Fig.8 Simulative curves by transfer function model and precise model for different fault locations
4 结语
本文提出了功能完善的自并励静止励磁系统精细模型建模方法,详细考虑了功率单元和励磁电源以及灭磁系统的建模,并在PSCAD/EMTDC中建立电磁暂态仿真模型,对灭磁功能和暂态稳定问题进行了仿真研究。
分析结果表明,在近机端或发生较严重的接地故障时,会导致机端电压降低,从而直接影响自并励静止励磁系统的励磁电源电压。因此,采用传递函数模型的励磁系统不能准确反映此类故障后的暂态特性,有必要采用考虑了功率单元和励磁电源特性的励磁系统精细模型。
致 谢
感谢PSCAD软件开发商Manitoba高压直流研究中心在同步电机仿真建模中提供的帮助!
[1]竺士章.发电机励磁系统试验[M].北京:中国电力出版社,2005:45-66.
[2]贺仁睦,沈峰,韩冬,等.发电机励磁系统建模与参数辨识综述[J]. 电网技术,2007,31(14):62-66.HE Renmu,SHEN Feng,HAN Dong,et al.The study of generator excitation system modeling and parameters estimation[J].Power System Technology,2007,31(14):62-66.
[3]汤涌. 基于电机参数的同步电机模型[J]. 电网技术,2007,31(12):47-51.TANG Yong.A discussion about standard parameter models of synchronous machine[J].Power System Technology,2007,31(12):47-51.
[4]CANAY I M.Determination of model parameters of synchronous machines[J].Electric Power Applications,IEE Proceedings B,1983,130(2):86-94.
[5]方思立,刘增煌.汽轮发电机自并励励磁系统的分析研究[J].电网技术,1997,21(12):33-37.FANG Sili,LIU Zenghuang.Analysis of bus fed static excitation system for turbogenerator[J].Power System Technology,1997,21(12):33-37.
[6]Energy Development and Power Generation Committee.IEEE recommended practice for excitation system models for power system stability studies:IEEE Std 421.5-2005[S].New York,USA:IEEE Power Engineering Society,2006.
[7]中国国家标准化管理委员会.同步电机励磁系统电力系统研究用模型:GB /T7409.2—2008[S]. 北京:中国标准出版社,2008.
[8]HURLEY J D.Comparative transient performance of rotating and static excitation systems[C]∥Proceeding of the American Power Conference.East Pittsburgh,USA:IEEE,1982:718-722.
[9]李基成.现代同步发电机励磁系统设计及其应用[M].北京:中国电力出版社,2002:145-167.
[10]梁建行,高光华,易先举,等.大型发电机灭磁系统设计的几个主要问题[J]. 人民长江,2011,42(15):86-91.LIANG Jianxing,GAO Guanghua,YI Xianju,etal.Several issues on de-excitation system design of large generators[J].Yangtze River,2011,42(15):86-91.
[11]梁建行.发电机灭磁系统几个技术要求的讨论[J].水电自动化与大坝监测,2005,29(3):45-50.LIANG Jianxing.Discussion on the technical requirements of de-excitation system for generators[J].Hydropower Automation and Dam Monitoring,2005,29(3):45-50.
[12]DOMMEL H W.电力系统电磁暂态计算理论[M].李永庄,林集明,曾昭华,译.北京:中国水利电力出版社,1991:214-215.
[13]张立霞,王高山,汪友华,等.暂态稳定分析典型励磁模型仿真研究[J]. 电力自动化设备,2008,28(1):77-79.ZHANG Lixia,WANG Gaoshan,WANG Youhua,et al.Simulation of typical excitation models for power system transient stability analysis[J].Electric Power Automation Equipment,2008,28
(continued on page 126)(continued from page 115)(1):77-79.
[14]付义,刘觉民,鲁文军.利用改进Prony算法的励磁调节器中PSS的设计[J]. 电力自动化设备,2011,31(4):82-86.FU Yi,LIU Juemin,LU Wenjun.Design of PSS for excitation regulator with improved Prony algorithm[J].Electric Power Automation Equipment,2011,31(4):82-86.
[15]PRABHA K.Power system stability and control[M].New York,USA:McGraw-Hill Education,1994:102-105.

