基于Tikhonov正则化方法的同步电机参数辨识

黄 操，袁海文，马 钊，凌 牧

（1.北京航空航天大学 自动化科学与电气工程学院，北京 100191；2．中国电力科学研究院，北京 100192）

0 引言

同步电机是电力系统中的重要部件，其运行行为影响到电力系统的各个方面，而掌握精确的电机参数，对准确分析和计算其动态行为有重要的意义。在实际工作过程中，电机的实际参数值并不是一成不变的，而是随着环境和工况的不断变化在一定范围内变化，如温度变化引起的集肤效应，会影响电机定、转子的电阻值，磁场饱和程度不同也会影响电感参数等。因此同步电机参数的辨识一直是电力系统研究的重要内容［1］。

传统的参数辨识算法中，最小二乘法是比较常用的算法，具有算法简单、易于理解、易于实现等优点，因此被广泛应用［2-4］。但最小二乘法存在一定的局限性，没有考虑到系统的病态性问题。所谓病态性问题就是系统数据微小的变化引起解的巨大变化［5］，当病态性严重时，算法会存在收敛性和多值性的问题，结果将偏离真实值。

由于同步电机也是高维非线性系统，其病态性是参数辨识过程中无法回避的问题。文献［6-8］都提到了同步电机系统的病态性，并采用子集选择法来克服系统的病态，但子集选择法有它的局限性，即需要一些先验知识来帮助确定哪些参数是固定的。本文将参数辨识看成是一种非线性反问题，反问题具有不适定性，也就是病态性问题，其求解过程就是解决病态性问题的一个过程［9］。在反演问题理论中，正则化是解决病态问题的基本思路，本文将经典的Tikhonov正则化方法引入到同步电机的参数辨识中，并通过在仿真中设置多个场景，证明了该方法能克服系统的病态性并有效地进行参数辨识。

1 病态性分析及其度量

一般而言，对于一个系统的模型，如果原始数据的微小变化引起解的巨大变化，则称该模型为病态的，反之则称为良态的。病态与良态，是模型本身固有的属性，它表征了模型抗干扰性的强弱，即稳定性的好坏［5］。

通常用条件数K来度量病态性的严重程度。统计应用经验表明：若01 000，则认为存在严重病态［5］。

引理 1 设若对Cn×n上的某一矩阵范数‖·‖有‖A-1‖‖δA‖＜1，则非齐次线性方程组 Ax=y与（A＋δA）（x＋δx）＝y+δy的解满足：

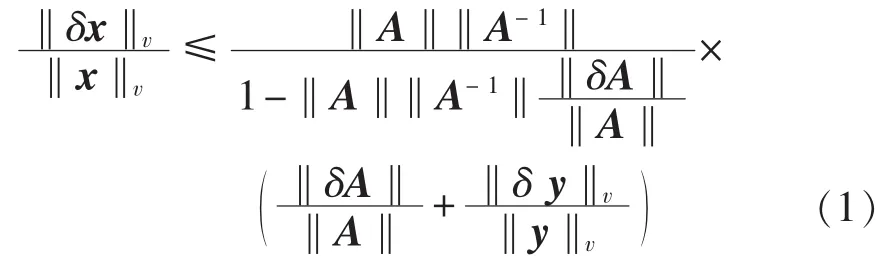
其中，‖·‖v为Cn上与矩阵范数‖·‖相容的向量范数，证明过程见文献［10］；δ为表征输出误差的参数。

由式（1）可以知道，数据的误差对逆矩阵和求解线性方程组解的影响与‖A‖‖A-1‖的大小有关，当‖A‖‖A-1‖较大时，近似逆矩阵或线性方程组的相对误差可能较大，因此‖A‖‖A-1‖可作为影响求解线性方程组解的大小的一种度量。

定义 1则称

为矩阵A的条件数。一般地，如果系数矩阵A的条件数大就称A对于求逆或求解线性方程组是病态的，否则称为良态。

2 反问题与Tikhonov正则化方法

2.1 反问题与参数辨识

反问题是相对于正问题而言的，一个先前被研究的相对充分或完备的问题称为正问题，而与此相对应的另一个问题称为反问题。从实际应用中来看，可以概括地说，有2种动机驱动着反问题的研究：想了解物理过程过去的状态或辨识参数；想了解如何通过干预当前的状态或调整某些参数去影响或控制该系统，以使其在未来到达人们所期望的状态［9］。

图1描述了反问题的基本原理，而参数辨识是指在输入和输出数据的基础上，从给定系统的数学模型中确立系统模型参数，因此参数辨识实际上就是一种典型的反问题。反问题求解面临2个根本困难：

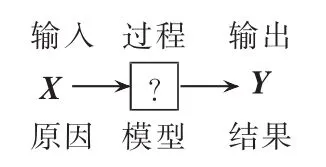
图1 反问题原理图Fig.1 Schematic diagram of inverse problem

a.用于反问题求解的原始数据可能不属于该问题的精确解所对应的数据集合，因而，在经典意义下的近似解可能不存在；

b.近似解的不稳定性，即原始数据小的观测误差（这个在工程中是不可避免的）会导致近似解与真解的严重偏离。

这是反问题求解中要面对的2个难点和关键所在，即所谓的反问题的不适定性。其中，a为反问题解的存在性问题，对于参数辨识而言，即是参数的可辨识问题［11］；b是关于解的唯一稳定问题，实际上也是病态性问题。反问题求解主要是解决病态性问题。而在反演理论中，正则化方法是解决病态问题的基本思路。

2.2 Tikhonov正则化方法

假设反问题可以用一个抽象的算子方程（3）来描述，其中x代表系统的未知量，y代表系统的输出，A为系统算子。反问题为：已知A和y来求未知量x。当A为线性算子，称其为线性反问题，否则为非线性的反问题：

求解反问题不适定性的普遍方法是：用一组与原不适定问题相“邻近”的适定问题的解去逼近原问题的解，这种方法称为正则化方法。如何建立有效的正则化方法是反问题领域中不适定问题研究的重要内容。解决不适定性的典型的方法是变分正则化方法，又称为 Tikhonov 正则化方法［9，12-13］。

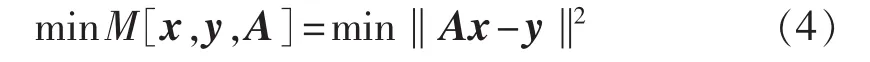
按照正则化思想，可以用一系列与问题式（3）相邻近的适定问题来近似，例如用下述带有参数α（α≥0）的极小化问题来近似：

称 Mα［x，y，A］为 Tikhonov泛函，α≥0 为正则参数，易见式（5）的欧拉方程为：

因此式（3）的极小解xα为正则解：

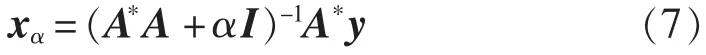
对于任何α≥0而言，其解存在、唯一，且连续依赖于A、y和α。则余下的工作是如何选取合适的正则参数α的问题。总体而言，正则参数α的选取要兼顾近似解的数值稳定性和与原问题的好的逼近程度这2个要求。

这里正则参数α主要采用MOROZOV偏差原理来获得，假设具体步骤如下［9］，其中 αn为第 n次迭代中的正则参数值，xαn，δ为第 n次迭代中的x值。

a.给定初始正则参数 α0≥0，令 n＝0。

（92）细齿羽苔 Plagiochila denticulata Mitt. 熊源新等（2006）；杨志平（2006）

b.解方程（A*A+αnI）xαn，δ=A*yδ，得 xαn，δ。

c.对步骤b中的方程求导得到方程：

求解该方程得

e.令 αn+1=αn-F（αn）/F′（αn），若小于某

指定精度，则计算终止，否则进入步骤f。

f.令 n=n+1，转步骤 b。

3 同步电机模型及病态性分析

同步发电机参数的计算依赖于数学模型的建立，模型不同参数也有所不同，本文选用同步发电机在dq旋转坐标系下的稳态方程（8）作为数学模型，同时忽略饱和、磁滞和涡流的影响，并且忽略阻尼绕组［14-15］。

其中，id、iq和 ud、uq分别为定子绕组 d、q 轴的电流和电压；if、uf分别为励磁绕组的电流和电压；Rs、Rf分别为定子绕组和励磁绕组电阻；Ld、Lq分别为定子绕组 d、q 轴上的自感；Lf为励磁绕组自感；Lmd、Lmq分别为定子绕组d、q轴与励磁绕组间的互感。

由式（8）可知，本文主要识别的参数为 Rs、Rf、Lq、Ld、Lf、Lmd、Lmq，因此式（8）可以写成如下形式：

其中，A为利用观察值建立的矩阵；输出y=［uduquf］T；参数矩阵 x=［LdLqLfLmdLmqRs］T，所以本文中的参数识别的反问题即为：已知A和y，求x。

同步发电机的数学模型的病态性主要表现为矩阵A的病态性，可以通过计算法矩阵ATA的条件数来度量系统病态的严重程度，条件数的计算可以采用式（2）。

本文将通过下一节的同步发电机实例的测试数据来计算法矩阵的条件数。由于矩阵A需要用到电流的微分量，所以必须进行离散化处理：i′= （i（k）-i（k-1））/Ts，其中 Ts为采样周期。 对同步电机的运行电流进行采样，就能确定矩阵A，然后通过式（2）就能计算得到条件数K。当Ts=1×10-4s时，计算得K=4.687×105。由此可知，系统的病态性严重。

4 参数辨识的仿真

4.1 仿真模型

为了获得同步发电机的测量数据，采用MATALB的Simulink平台［16］搭建了同步发电机模型，其中电机采用Simulink自带的同步电机模型，反问题的Tikhonov正则化方法采用S-function来编写，并作为一个模块嵌入到同步发电机系统仿真环境中，主要实现对发电机参数的识别。电机的参数为某航空独立交流电源中主发电机的实际参数，如表1所示。

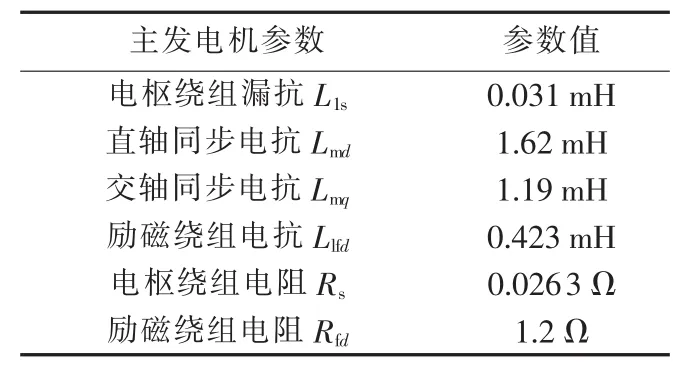
表1 主发电机参数Table 1 Parameters of master generator

4.2 仿真分析

为了真实地模拟观测数据，并验证Tikhonov正则化方法求解病态问题的能力以及对参数辨识的有效性，分别对测量数据加入10%、20%、30%的Gauss白噪声，即：

由式（9）可知，反问题的输入为电机模型输出的iq、id、if、uq、ud、uf，如图 2 所示（图 2 所示为 t=0.1 s 时机械功率Pm阶跃增大时的发电机电流、电压波形），然后通过反问题的正则化方法，计算出同步电机的参数 Rs、Rf、Lq、Ld、Lf、Lmd、Lmq，其中 Ld＝L1s+Lmd，Lq＝L1s+Lmq，Lf＝ L1fd+Lmd。

本文采用MOROZOV偏差原理来求解正则化参数α。选取正则参数α必须非常小心，如果α太大，则新得到的问题对原问题的逼近程度太差；相反如果α太小，则问题的不适定性并没有克服，数值计算仍然很不稳定。

a.加入10%白噪声：表2是在测量数据中加入10%白噪声后的辨识结果，经过迭代最终得到正则参数α=1.36×10-3，迭代次数为8。由表中数据可以看出辨识结果较好。

b.加入20%白噪声：表3是在测量数据中加入20%白噪声的辨识结果，经过迭代最终得到正则参数α=8.65×10-3，迭代次数为16。由表中数据可以看出辨识结果虽然不太精确，但可以接受。

c.加入30%白噪声：表4是在测量数据中加入30%白噪声的辨识结果，经过迭代最终得到正则参数α=3.64×10-2，迭代次数为20。30%白噪声代表比较严重的工况，由表中数据可以看出辨识结果开始偏离真实值。

图2 电流、电压波形Fig.2 Current and voltage waveforms

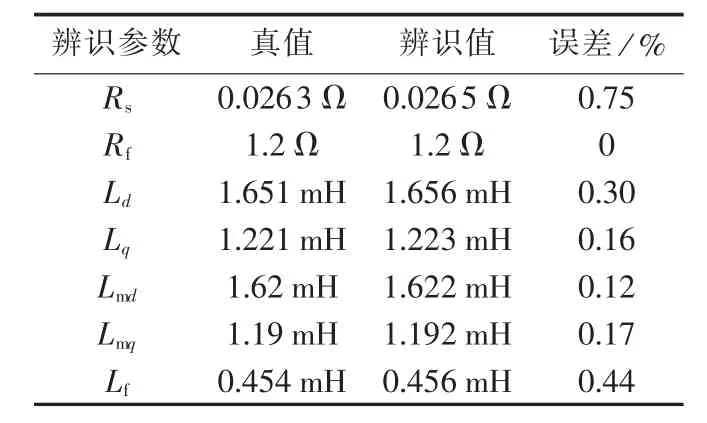
表2 加入10%噪声的辨识结果Table 2 Results of identification with 10%noise

表3 加入20%噪声的辨识结果Table 3 Results of identification with 20%noise

表4 加入30%噪声的辨识结果Table 4 Results of identification with 30%noise

4.3 与传统最小二乘法的比较

如何建立有效的正则化方法是反问题领域中病态问题研究的重要内容。通常的正则化方法有Tikhonov正则化方法、信赖域法、正则化的内积法等，Levenberg-Marquardt［17］也是一种特殊的正则化方法，可以看作是对非线性问题作先线性化后正则化的过程，文献［9］对它的正则化进行了证明。本文选择的是经典的Tikhonov正则化方法。传统的参数辨识方法中，使用最多的是最小二乘辨识法以及一些改进的最小二乘法，如增广二乘法、广义最小二乘法、加权最小二乘法，与它们相比，本文方法的本质区别在对系统病态性能力的克服上，这里通过Tikhonov正则化方法与最小二乘辨识法的比较来进行证明。对于系统 Y=AX，X 的最小二乘解是 x=（ATA）－1ATy，而正则解为 xα=（ATA+αI）－1ATye。 系统的病态表现为矩阵A的病态，即法矩阵ATA的病态性。与最小二乘法相比，正则化方法增加了αI一项，这一项的引入使法方程的病态性得到改善，因而能得到好的估计值。

表5显示了对测量数据加入10%、20%、30%的白噪声，并采用最小二乘法进行辨识的同步电机参数值。可以看出，在10%的白噪声污染下，最小二乘法的结果已经开始偏离，但勉强可以接受，而在强噪声（30%的白噪声污染）的工况下，最小二乘法的辨识结果已经完全偏离真实值。由此可知，Tikhonov正则化方法克服病态性的能力优于最小二乘法。

表5 加入噪声的最小二乘法辨识结果Table 5 Results of identification with noise by least square method

5 结论

本文将同步电机的参数辨识作为一种反问题来研究，而反问题首要解决的问题就是病态性问题。通过对系统病态性问题的分析，得出正则化方法是解决病态问题的基本思路，将反演理论中经典的Tikhonov正则化方法引入同步发电机参数辨识中，为同步发电机参数辨识问题提供了一条新的有严格数学理论基础的思路和方法。通过实验研究，并与传统的最小二乘法相比较，可以证明：该方法能有效地进行参数辨识，同时具有克服病态性的能力。

［1］沈善德.电力系统辨识［M］.北京：清华大学出版社，1993：65-101.

［2］BJORCK A.Least squares methods［M］.Amestertam，Netherlands：Elesvier Science Ltd.，2002：466-645.

［3］KARRARI M，MALIK O P.Identification of physical parameters of a synchronous generator from online measurements［J］.IEEE Transactions on Energy Conversion，2004，19（2）：407-415.

［4］唐昆明，康丽红，殷家敏.基于可测量的同步发电机参数时域辨识［J］. 电力自动化设备，2014，34（8）：135-146.TANG Kunming，KANG Lihong，YIN Jiamin.Time-domain parameter identification based on measurable variables for synchronous generator［J］.Electric Power Automation Equipment，2014，34（8）：135-146.

［5］张永军，吴磊，林立文，等.摄影测量中病态问题的条件数指标分析［J］. 武汉大学学报信息科学版，2010，35（3）：308-312.ZHANG Yongjun，WU Lei，LIN Liwen，et al.Condition numbers forevaluation ofill-posed problems in photogrammetry ［J］.Journal of Wuhan University Information Science，2010，35（3）：308-312.

［6］BURTH M，VERGHESE G C，VELEZ-REYES M.Subset selection for improved parameter estimation in on-line identification of a synchronous generator［J］.IEEE Transactions on Power Systems，1999，14（1）：218-225.

［7］VELEZ-REYES M，JAUREGUI L.Conditioning analysis of parameter estimation in a synchronous generator［C］∥Proceedings of the 2001 IEEE International Electric Machines and Drives Conference（IEMDC 2001）.Cambridge，MA，USA：IEEE，2001：285-291.

［8］NINO C E，VELEZ-REYES M.Dealing with ill conditioning in recursive parameter estimation for a synchronous generator ［C］∥IECON 2006-32nd Annual Conference on Industrial Electronics.Paris，France：IEEE，2006：1089-1094.

［9］王彦飞.反演问题的计算方法及其应用［M］.北京：高等教育出版社，2007：13-60.

［10］戴华. 矩阵论［M］. 北京：科学出版社，2001：30-63.

［11］李靖霞，倪腊琴，鞠平，等.同步电机参数的可辨识研究［J］.电力系统自动化，1998，22（3）：9-12.LI Jingxia，NI Laqin，JU Ping，et al.A study on the identifiability of synchronous generator parameters［J］.Automation of Electric Power Systems，1998，22（3）：9-12.

［12］TIKHONOV A N，ARSENIN V Y.Solutions of ill-posed problems［M］.New York，USA：John Wiley and Sons，1997：200-215.

［13］ENGL H W，NEUBAUER H M.Regularization of inverse problems［M］.Dordrecht，Netherlands：Kluwer，1996：50-55.

［14］陈世元.电机学［M］.北京：中国电力出版社，2004：73-90.

［15］谢军.航空电机学［M］.北京：国防工业出版社，2006：202-214.

［16］于群，高娜.Matlab/Simulink电力系统建模与仿真［M］.北京：机械工业出版社，2011：153-180.

［17］HANKE M.A regularizing Levenberg-Marquardt scheme，with application sto inverse groundwaterfilteration problems［J］.Inverse Problems，1997（13）：79-95.