基于暂降信息的监测装置优化配置与系统电压暂降水平评估

林 芳 ，肖先勇 ，张 逸 ，邱玉涛 ，吴丹岳

（1.四川大学 电气信息学院，四川 成都 610065；2.国网福建省电力有限公司电力科学研究院，福建 福州 350007）

0 引言

电压暂降是电力系统不可避免的电能质量扰动事件，被认为是最严重的电能质量问题［1］。以必要的监测数据为基础的系统电压暂降水平评估是科学决策的前提，故提出科学的监测装置优化配置和系统暂降水平评估方法，具有重要理论价值和现实意义。

现有电压暂降评估方法主要有实测法［2］、仿真模拟法［3-5］及状态估计法［6-7］等。 其中，实测法所得结果可靠，但安装和运行维护成本高；仿真模拟法基于故障率、故障位置和故障类型的历史统计数据进行电压暂降仿真，结果仅在统计意义上成立［6］；状态估计法结合实测法与仿真模拟法的优点，以必要的监测数据为基础，通过状态估计方程对全网各节点电压暂降频次进行估计。但现有状态估计法仅考虑了全网节点暂降频次的可观性，忽略了暂降事件的其他信息。事实上，监测或仿真模拟可得到暂降事件的幅值、持续时间、能量损失等诸多信息，在此基础上可依次得到节点指标和系统指标［8-9］，仅用特定幅值区间及频次描述节点和系统暂降水平显然不够全面。因此，研究单一事件信息、节点指标、系统指标的内在联系，提出科学的监测装置优化配置方法，是合理、客观、全面评估系统电压暂降水平的关键。

本文引入暂降信息概念，根据监测或仿真可获得的幅值、频次、能量损失、敏感设备兼容程度等信息构造节点指标向量和系统指标向量，分别用以刻画节点和系统暂降水平；研究了节点指标和系统指标之间的关系，提出可基于抽样思想，以代表性节点监测代替全网监测，评估系统暂降水平；以仿真模拟法所得节点指标向量为节点分区依据，并通过粒子群K均值聚类算法进行节点分区和代表性节点识别；用代表性节点的指标向量度量所代表分区的电压暂降水平，通过统计方法估计系统指标向量。对IEEE 30节点系统进行仿真，并与现有方法比较，结果表明，本文方法所需监测装置数量少，评估结果准确，能可靠获得电压暂降系统指标，合理评估系统电压暂降水平，且对系统故障率和故障随机分布的适应性强。

1 系统暂降水平评估流程与关键问题

1.1 节点暂降指标

为充分利用监测或仿真结果，引入暂降信息概念，即对监测或仿真所得单一事件数据进行处理，可得到的暂降基本特征量、扰动源位置及类别、暂降对用户的影响程度等信息。针对电压暂降水平评估，IEEE P1564—2014标准对单一暂降事件信息提出量化指标的计算方法，并基于单一暂降事件信息计算节点暂降指标［9］。常采用的节点暂降指标如下。

a.期望暂降幅值。

期望暂降幅值ESM（Expected Sag Magnitude）为某一节点n次暂降的平均幅值［4］，记作RESM：

其中，n为监测周期内该节点发生的暂降事件总数；Ui为该节点n个暂降事件中第i个暂降事件幅值。

b.系统平均均方根值变化频率指标。

系统平均均方根值变化频率指标SARFI（System Average RMS variation Frequency Index）包括SARFIx和SARFICurve。SARFIx表示监测周期内某一节点发生暂降幅值低于参考电压x%的暂降频次；SARFICurve表示节点发生落在敏感设备耐受曲线下方的暂降频次，常用 SARFICBEMA、SARFIITIC、SARFISEMI等指标。

c.平均暂降能量损失。

平均暂降能量损失指标ASEI（Average Sag Energy Index）表示监测周期内某一节点所有暂降事件的平均能量损失，记作RASEI：

其中，Ti为该节点第 i个暂降事件的能量损失，Ti为第i个暂降事件持续时间。

d.平均暂降严重性指标。

平均暂降严重性指标ASSI（Average Sag Severity Index）反映某一节点暂降水平与敏感设备的兼容程度，记作 RASSI：

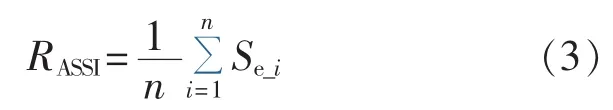
其中，为该节点第i个暂降事件的严重性指标，UCurve（Ti）为敏感设备耐受曲线上持续时间Ti对应的电压限值，Se_i＞1时说明该次暂降事件落于敏感设备耐受曲线下方，影响敏感设备正常工作，且其值越大，表明暂降越严重。

1.2 系统暂降水平评估

结合IEEE P1564—2014标准推荐方法，给定电网节点和系统电压暂降水平评估流程如图1所示。

图1 电压暂降评估流程图Fig.1 Flowchart of sag assessment

单一事件暂降信息、节点指标和系统指标分别从事件、节点和系统3个层面对电压暂降水平进行刻画，其中系统指标确定方法有2种。

a.系统指标为节点指标的加权平均值：

其中，sj为第j项系统指标值；xij为节点i的第j项指标值；m为节点数；hi为节点i的权重。权重需根据系统和负荷信息确定，为简化，本文对所有节点赋予统一权重，即任意 i∈［1，2，…，m］，取 hi=1［9］。

b.系统指标为节点指标的95%概率大值（CP95值），即针对某一指标，若95%的节点该项指标值不超过L，则将L作为该项指标的系统指标值。

1.3 关键问题

就系统指标而言，加权平均值或CP95值均需获得全部节点指标，而实际中不可能对所有节点进行监测，因此基于必要监测和仿真的状态估计法具有明显优势。但现有暂降状态估计方法基于暂降可观测区域MRA（Monitor Reach Area）原理确定监测装置安装数量和位置［10-12］，仅考虑了节点是否发生幅值低于设定阈值的电压暂降事件的可观性，导致较多暂降信息的删失。

当监测装置安装数量有限并期望得到较全面、准确的系统暂降水平评估结果时，可基于抽样思想，用代表性节点监测代替全网监测，根据代表性节点的暂降信息估计系统暂降水平，如图2所示。监测节点的代表性越高，系统暂降水平评估结果的可靠性就越高［13］。因此，分析系统中所有节点暂降水平的相似或相异程度，选定能反映整个系统暂降水平的代表性节点，是实现该方法有效性的关键。

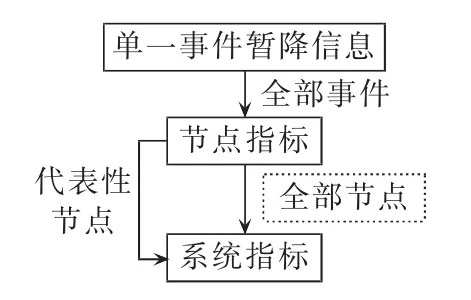
图2 基于抽样思想的代表性节点方法示意图Fig.2 Schematic diagram of representative site method based on sampling concept

为揭示节点之间暂降水平相对优劣关系及其隐含规律，选取合适的代表性节点，可从以下3个方面进行考虑：

a.引入考虑幅值、频次、能量损失、与敏感设备兼容程度等暂降信息的多维节点指标向量表征节点暂降水平，弥补独立单一指标的不足；

b.选用适当的多指标分析方法，分析节点暂降水平相似或相异程度，获得节点分区方案；

c.在每个分区中选择代表性节点作为监测节点，根据监测节点获得的暂降信息评估所在分区的暂降水平和系统暂降水平。

2 节点分区方法

2.1 节点指标向量

构造d维节点指标向量Bi表征节点i暂降水平：

其中，xi1、xi2、…、xid为节点 i指标向量各项指标。 考虑到大部分暂降幅值高于0.5 p.u.［14］，本文选取期望暂降幅值指标RESM，系统平均均方根值变化频率指标SARFI90、SARFI70、SARFI50、SARFICurve，平均 暂 降能量指标RASEI，平均暂降严重性指标RASSI这7个指标构造节点指标向量。SARFICurve、RASSI涉及敏感负荷耐受曲线，可根据关心的敏感负荷类型选择CBEMA、ITIC、SEMI F47等曲线。根据实际需要还可对指标进行合理增删。

式（5）形式的节点指标向量可由实际监测或仿真模拟得到，在未安装监测装置情况下，仿真模拟是获得该向量的唯一途径，记为

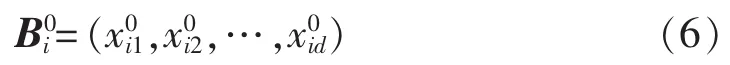
图3以期望暂降幅值指标RESM（标幺值）为例，说明节点实际暂降水平与仿真模拟法结果之间的关系。采用蒙特卡罗方法进行仿真［4］，其中节点1为负荷节点，节点2为发电机节点。随着仿真年份增多，RESM仿真值分别收敛于稳定值f1和f2，而RESM实际值则以稳定值为基准在一定范围内波动。因此可认为，特定监测周期内节点暂降水平实际值Bi是仿真值与实时波动量Δbi的叠加，即：

仿真模拟法以历史故障统计数据为基础，故其结果在长时间尺度上具有收敛性，能稳定反映该节点的固有暂降水平。因此，研究节点之间固有暂降水平的相对优劣关系，可具体化为对节点指标向量的处理分析。

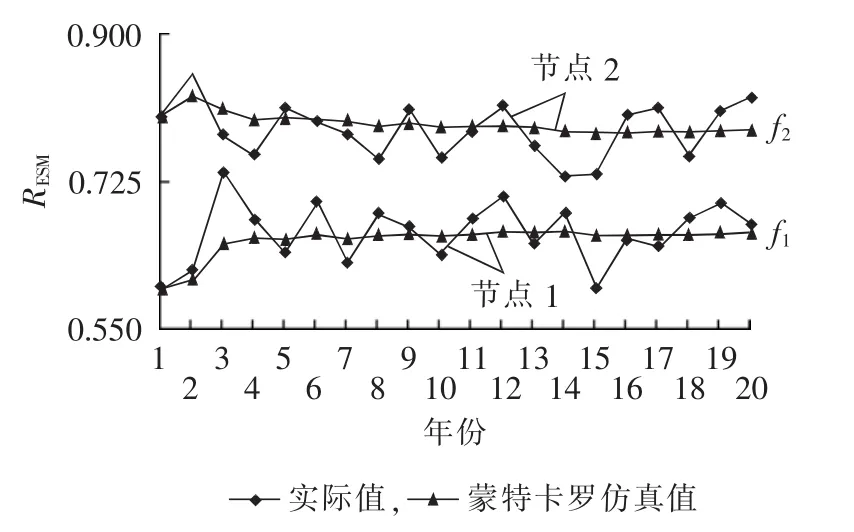
图3 节点RESM指标实际值与仿真值对比Fig.3 Comparison of site RESMindex between actual and simulative values

2.2 基于聚类分析的节点分区

2.2.1 数据处理

以节点固有暂降水平为依据的节点分区问题可描述为一种典型的空间聚类问题，即将系统全部节点分为若干个集合，同一集合内节点的暂降水平最大限度地相似，不同集合节点的暂降水平最大限度地不同［15］。为消除组成节点指标向量的各指标之间不同数量级和量纲对聚类的影响，首先将仿真模拟所得各指标进行归一化处理：

其中，yij为归一化后的指标；为节点i的第j项指标；为全部节点第j项指标的平均值；为第j项指标的标准差。

数据归一化处理后，节点i指标向量为Yi=（yi1，yi2，…，yid）。系统中所有节点指标向量组成样本集：

任意2个节点i与j之间暂降水平的差异可用节点暂降水平距离 d（Yi，Yj）表示：

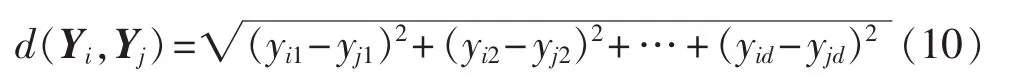
2.2.2 粒子群K均值聚类

节点聚类问题就是要找到一个划分C=｛C1，C2，…，Ck｝，满足以下条件：

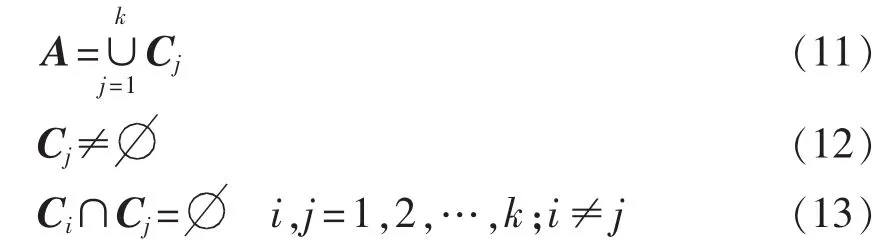
并使类内距离函数JC最小：

其中，为分区 Cj的聚类中心，mj为 Cj包含的节点数；d（Yi，Zj）为分区 Cj内节点 Yi到该分区聚类中心的距离。

K均值算法是使用最广泛的聚类算法之一，但由于初始聚类中心选择的随机性，易过早收敛到局部最优。粒子群K均值聚类算法通过给聚类中心增加扰动，可大幅增强其跳出局部极值和寻找最优聚类的能力［16］。基于粒子群K均值聚类算法的节点分区步骤如下。

a.由仿真模拟法得到各节点指标向量仿真值，通过数据归一化处理，得样本集A。

b.生成初始种群。将所有节点随机分配给k个分区，计算每个分区节点指标向量均值作为该分区初始聚类中心，并串联k个聚类中心作为该粒子的位置编码，同时随机初始化粒子速度，如此反复N次，生成包含N个粒子的初始种群。第i个粒子的位置表示为 Wi= （Z1，Z2，…，Zk），速度表示为 Vi= （v1，v2，…，vk）。

c.根据最近邻原则进行新的聚类划分，即若样本 Yi、聚类中心 Zj满足

则Yi属于分区Cj。根据式（14）计算类间总离散度JC作为粒子适应值，JC越小，则适应值越好。

d.每个粒子，比较当前位置的适应值和它经历过的最好位置Pi的适应值，如果更小，则更新Pi；比较当前位置的适应值和群体所有粒子经历过的最好位置Pg的适应值，如果更小，则更新Pg。

e.根据式（16）、（17）更新粒子的速度和位置：

其中，分别为在第r+1次迭代中第i个粒子的速度和位置；ω为惯性权重；c1、c2为学习因子；rand（）为 0～1 之间的随机数。

f.根据新产生粒子的位置，按最近邻原则确定新的聚类划分；重新计算每个聚类的聚类中心取代原来粒子的位置编码，并计算JC。

g.判断是否达到结束条件。若聚类中心不再发生变化或达到最大迭代次数M，则终止算法；否则转入步骤d。

h.根据最终聚类结果确定节点分区方案。

3 监测装置配置及系统暂降水平评估

3.1 监测点选择及系统指标向量估计

本文选取系统指标为节点指标的均值形式。为准确估计系统指标，代表性监测节点应具备2个条件：通过监测点能较好地观测所在分区的暂降水平；所有监测点指标向量的均值应最大限度地接近系统指标向量实际值。因此，本文选取每个分区中距该分区聚类中心最近的节点为代表性节点，即若分区Cj内节点f满足式（18），则在节点f安装监测装置。

若最终监测节点集合为P，则系统指标向量估计值Se为：

其中，Bs为监测节点s指标向量实际值。Se第j项指标sej计算式为：

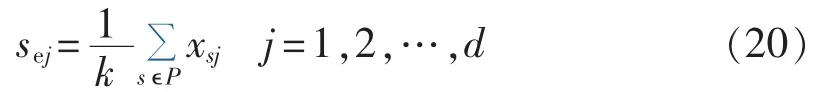
3.2 估计误差

由于实际系统中尚未安装监测装置，为验证本文方法的有效性，随机模拟一年的短路故障得到所有节点暂降指标向量 Bi（i=1，2，…，m），并将其作为实际值，则系统指标向量实际值Sr第j项指标srj为：

系统第j项指标的估计误差及d维系统指标向量平均估计误差分别如式（22）、（23）所示：

显然，当聚类数k=m，即在每个节点都安装监测装置时，可以获得最准确的系统指标。然而，考虑经济性原则，应在估计精度满足要求的情况下选择最少的聚类数。若给定估计精度ε，可从k=2开始增加聚类数进行反复试验，当对于任意 j∈［1，2，…，d］，都有 δj＜ε 时停止。

综上所述，监测装置优化配置及系统暂降水平评估流程如图4所示。

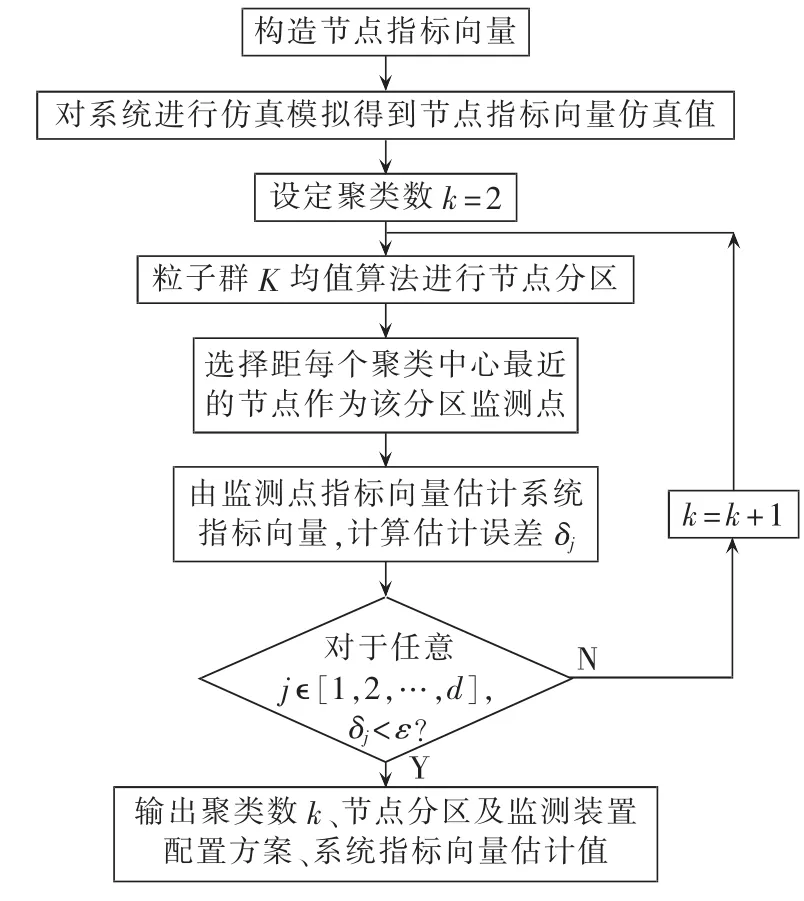
图4 监测装置配置和系统暂降水平评估流程图Fig.4 Flowchart of monitor allocation and system sag level assessment

4 算例仿真

应用本文方法对图5所示IEEE30节点系统进行仿真。系统元件故障率、各序参数、线路长度等数据参见文献［17］。设132 kV侧故障清除时间为0.1～0.5 s，33 kV 侧故障清除时间为 0.5～0.9 s［14］。 以计算机为关心敏感负荷，选取ITIC曲线计算SARFICurve、RASSI指标。设置粒子群K均值算法中粒子数N为50，最大迭代次数 M 为 50；学习因子 c1、c2均取 2，惯性权重 ω 采用可变权重［16］：

其中，r为当前迭代数；ωmax=0.9；ωmin=0.4。

4.1 节点指标向量仿真值

构造节点暂降指标向量，其中，除期望暂降幅值指标RESM为正向指标，即值越大越好外，其余指标均为负向指标。以短路故障导致的电压暂降为研究对象，对系统进行10000次蒙特卡罗仿真，计算各节点指标向量仿真值，作为节点分区及代表性节点选取的依据，如表1所示。

图5 IEEE 30节点测试系统Fig.5 IEEE 30-bus test system

表1 节点指标向量仿真值Table 1 Simulative site index vectors

4.2 节点分区及监测装置配置

基于粒子群K均值聚类算法，确定系统的节点分区和监测装置配置方案。设ε=10%，经计算当聚类数k取4时各系统指标估计误差均小于ε。节点分区及监测装置配置方案如表2所示。

表2 节点分区和监测装置配置方案Table 2 Site partition and monitor allocation scheme

监测装置安装节点为5、16、20、27。用各分区监测点的指标向量表征该分区暂降水平，如表3所示。从表3可知，分区1的所有暂降指标均优于其他分区，可认为该分区暂降水平最优。暂降水平优劣排序为分区1>分区2>分区3、分区4。从实际电网拓扑来看，分区1的节点均连接发电机，具有较强的电压支撑能力，因此暂降最不严重；分区2包括132 kV的非发电机节点及33 kV邻近发电机的节点，因此其暂降水平劣于分区1；分区3、4的节点均为远离发电机的负荷节点，受系统故障影响程度较大，暂降水平最劣。分区结果与电网实际情况相符，验证了本文方法的正确性和有效性。

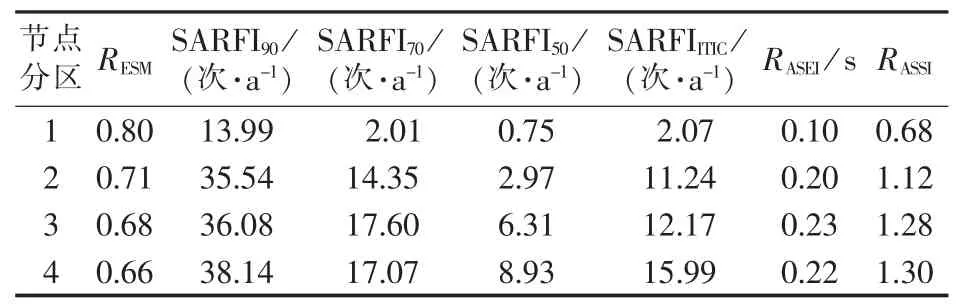
表3 各分区暂降水平Table 3 Sag level of each partition

4.3 方法对比

4.3.1 与MRA法对比

在MRA法中设置暂降阈值分别为0.9 p.u.和0.8p.u.，对应监测装置配置方案为方案1和方案2，并与本文方法所得配置方案对比，结果如表4所示。

表4 本文方法与MRA法监测装置配置方案对比Table 4 Comparison of monitor allocation scheme between proposed method and MRA method

利用各监测方案评估系统暂降水平。根据系统故障率，模拟某年发生40次短路故障。本文方法与MRA法估计误差对比结果如表5、表6所示。从表4—6可知，0.9p.u.暂降阈值时，MRA法所得监测方案只比本文方法少安装1台监测装置，但系统暂降指标估计误差过大；0.8p.u.时误差在可接受范围内，但监测点数量是本文方法的2倍。可见，本文方法能有效减少监测点数量，同时保证系统暂降指标估计精度较高。

表5 本文方法与MRA法系统暂降指标向量估计误差对比Table 5 Comparison of system index vector estimation error between proposed method and MRA method

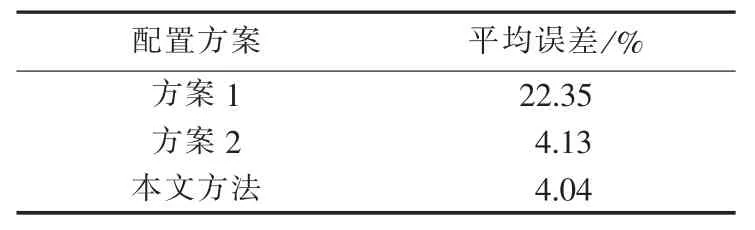
表6 本文方法与MRA法平均误差对比Table 6 Comparison of average error between proposed method and MRA method

4.3.2 与仿真模拟法对比

假设IEEE30节点系统连续15 a的实际故障率如表7所示，其中故障率相同的3 a其故障分布不同；而仿真模拟法对应的历史统计故障率为15 a实际故障率的平均值，为40次/a。以系统SARFI70指标为例，实际值、本文方法估计值及蒙特卡罗仿真值如图6所示。当每年的故障率或故障分布改变时，蒙特卡罗法所得系统暂降指标仿真值与实际值偏差较大，而本文方法确定的系统暂降指标估计值与实际值偏差较小，证明本文方法精度更高，对故障率和故障分布变化的适应性更强。

表7 各年份故障率Table 7 Fault rate for each year

图6 系统SARFI70指标变化情况Fig.6 Variation of system SARFI70index

图7 分区2、3 SARFI70指标变化对比Fig.7 Comparison of SARFI70index variation for Partition 2 and 3

监测点数据除了用以确定系统暂降指标外，还能反映所属分区的暂降水平，图7以SARFI70指标为例说明。在不同的故障率及故障分布下，分区2与分区3的SARFI70指标实际值有相似的变化趋势。用监测节点16、20的监测值分别估计分区2和分区3指标，与蒙特卡罗仿真结果相比，更能反映暂降水平的实际变化情况。

5 结论

a.引入暂降信息和多维暂降指标向量的概念，用幅值、频次、能量损失、敏感设备兼容程度等信息定量刻画节点和系统暂降水平，比单一指标方法更加全面准确；

b.基于粒子群K均值聚类算法得到合理、有效的节点分区和监测装置配置方案，在保证系统暂降指标估计精度的同时，有效减少了监测点数量；

c.对代表性节点进行监测，不仅能得到系统暂降指标，还能得到监测点所在分区的暂降指标，有助于运行人员从整体和局部两方面掌握暂降水平；

d.本文方法对系统内元件故障率和故障分布变化的适应性更强，具有一定的工程应用价值。

［1］刘旭娜，肖先勇，汪颖．电压暂降严重程度及其测度、不确定性评估方法［J］．中国电机工程学报，2014，34（4）：644-658．LIU Xuna，XIAO Xianyong，WANG Ying．Voltage sag severity and its measure and uncertainty evaluation［J］．Proceedings of the CSEE，2014，34（4）：644-658．

［2］李妍，余欣梅，熊信艮，等．电力系统电压暂降分析计算方法综述［J］．电网技术，2004，28（14）：74-78．LI Yan，YU Xinmei，XIONG Xinyin，et al．A survey on calculation and analysis methods of voltage sag ［J］． Power System Technology，2004，28（14）：74-78．

［3］BOLLEN M H J，QADER M R，ALLAN R N.Stochastical and statistical assessment of voltage dips［C］∥IEEE Colloquium on Tools and Techniques for Dealing with Uncertainty．London，UK：IET，1998：5/1-5/4．

［4］FARIED S O，BILLINTON R，ABORESHAID S．Stochastic evaluation of voltage sag and unbalance in transmission systems［J］．IEEE Transactions on Power Delivery，2005，20（4）：2631-2637．

［5］肖先勇，马超，李勇．线路故障引起电压凹陷的频次最大熵评估［J］．中国电机工程学报，2009，29（1）：87-93．XIAO Xianyong，MA Chao，LIYong．Voltagesagoccurrence frequency assessment caused by line faults using the maximum entropy method［J］．Proceedings of the CSEE，2009，29（1）：87-93．

［6］ESPINOSA J E，HERNANDEZ A．A method for voltage sag state estimation in power systems［J］．IEEE Transactions on Power Delivery，2007，22（4）：2517-2526．

［7］HERNANDEZ A，ESPINOSA J E，de CASTRO R M，et al．SVD applied to voltage sag state estimation［J］．IEEE Transactions on Power Delivery，2013，28（2）：866-874．

［8］SABIN D D，BOLLEN M H J．Overview of IEEE Std 1564-2014 guide for voltage sag indices［C］∥2014 IEEE 16th International Conference on Harmonicsand QualityofPower．Bucharest，Romania：IEEE，2014：497-501．

［9］Voltage S ag Indices Task Force ofthe Transmission and Distribution Committee.Draft guide for voltage sag indices：IEEE 1564-2014 ［S］.New York，USA：Electrical and Electronics Engineers，Inc，2014.

［10］OLGUIN G，VUINOVICH F，BOLLEN M H J.Anoptimal monitoring program for obtaining voltage sag system indexes［J］.IEEE Transactions on Power Systems，2006，21（1）：378-384.

［11］吕伟，田立军.基于凹陷域分析的电压暂降监测点优化配置［J］.电力自动化设备，2012，32（6）：45-50.LU¨ Wei，TIAN Lijun.Optimal allocation of voltage sag monitoring based on exposed area analysis ［J］.Electric Power Automation Equipment，2012，32（6）：45-50.

［12］邱玉涛，肖先勇，熊茜，等.基于临界阻抗和广度优先-条件搜索的暂降监测装置优化配置［J］. 电力自动化设备，2014，34（10）：138-143.QIU Yutao，XIAO Xianyong，XIONG Qian，et al.Optimal sag monitor placement based on critical impedance and breadth first-condition search［J］.Electric Power Automation Equipment，2014，34（10）：138-143.

［13］CAO Y，LARSEN D P.Comparison of ecological communities：the problem of sample representativeness［J］.Ecological Monographs，2001，72（1）：41-56.

［14］杨晓东，李庚银，周明，等.不确定条件下的电压暂降概率评估［J］. 电网技术，2010，34（2）：41-45.YANG Xiaodong，LIGengyin，ZHOU Ming，etal.Probability assessment of voltage sag under uncertain conditions［J］.Power System Technology，2010，34（2）：41-45.

［15］郭庆来，孙宏斌，张伯明，等.基于无功源控制空间聚类分析的无功电压分区［J］. 电力系统自动化，2005，29（10）：36-40.GUO Qinglai，SUN Hongbin，ZHANG Boming，etal.Power network partitioning based on clustering analysis in Mvar control space［J］.Automation of Electric Power Systems，2005，29（10）：36-40.

［16］刘靖明，韩丽川，侯立文.基于粒子群的K均值聚类算法［J］.系统工程理论与实践，2005，25（6）：54-58.LIU Jingming，HAN Lichuan，HOU Liwen.Cluster analysis based on particalswarm optimization algorithm ［J］.Systems Engineering-theory and Practice，2005，25（6）：54-58.

［17］PARK C H，JANG G.Stochastic estimation of voltage sags in a large meshed network ［J］.IEEE Transactions on Power Delivery，2007，22（3）：1655-1664.