基于多直流落点系统稳定性的电网静态分区方案选择方法

程斌杰 ，徐 蔚 ，徐 政

（1.浙江大学 电气工程学院，浙江 杭州 310027；2.广东电网公司 电网规划研究中心，广东 广州 510080）

0 引言

我国资源和负荷呈逆向分布，因此需要采取远距离大容量输电以实现跨区域能源资源的优化配置。高压直流输电技术以其在技术性和经济性上的优势成为跨区域、远距离联网的优选方案。在我国“西电东送”的基本格局下，出现了直流落点密集的受端系统，如华东电网和广东电网等，由于多直流落点受端系统的交直流相互作用复杂、直流馈入功率大，系统安全稳定性面临较大风险［1-2］。故障引起多条直流同时发生换相失败是多直流落点系统突出的安全稳定问题［3］，该类故障将造成受端系统功率大量缺失，从而可能导致系统失稳。目前，主要有以下几种方式可提高多直流落点系统的安全稳定性能：①受端电网动态分区［4］；②受端电网利用储能设备分区［5］；③故障期间改变直流控制方式［6-7］；④受端电网静态分区。其中方式①—③无法彻底解耦换流站之间电气联系。电网的静态分区技术通过柔性直流输电系统［8-9］将受端系统分隔成若干个异步运行的分区电网，从而使得各直流落点处于不同的分区电网内，不同分区之间的传统直流换流站基本不存在相互作用，故障影响范围限制在分区之内，该方式可有效解决故障引起多条直流同时换相失败的问题，此外，静态分区还能有效控制区间潮流以及防止短路电流超标。

不同的静态分区方案对受端系统性能的提升作用不同，有必要基于系统稳定性对各个静态分区方案进行评估和选择。系统的稳定性涉及多个方面，因此静态分区方案的选择是一个多目标决策问题。电力系统中无功优化问题［10-13］、分布式电源接入［14］、最优潮流［15］、直流落点选择［16］、水火电调度［17］均涉及多目标决策问题。多目标决策问题有多种求解方法，文献［11-12］运用粒子群优化算法对多目标的无功优化问题进行分析，文献［16］运用加权和法选择合理的直流落点，文献［17］采用数据包络分析CCR（Charnes-Cooper-Rhodes）模型对多目标问题进行求解。多直流落点系统静态分区方案的选择作为电力系统中的多目标决策问题，目前没有相关的研究，这给实际工程的规划带来了困难，因此有必要对电网静态分区方案的选择方法进行研究。

本文首先分析了影响多直流落点受端系统稳定性的3个问题，包括多直流发生换相失败问题、直流换相失败后系统恢复问题以及直流闭锁问题，在此基础上针对性地提出了反映系统稳定性的3个指标及相应的子指标；其次建立了用于评价静态分区方案的线性加权和模型［18］，将多目标模型转换成单目标模型，并采用兼顾主客观的综合赋权法确定3个指标和其子指标的权重系数；再次建立了基于多直流落点系统稳定性的电网静态分区方案选择方法；最后以2030年广东电网规划网架为例，对静态分区的方案进行选择，并通过PSS／E仿真平台对各方案的系统稳定性进行仿真，验证了静态分区方案选择方法的有效性。本文提出的静态分区方案选择方法对于实际工程中静态分区方案的确定具有指导意义。

1 静态分区

静态分区利用柔性直流输电技术（VSC-HVDC）将电网分隔成若干个异步运行的分区电网，多直流落点系统静态分区示意图如图1所示，其中分区之间为柔性直流输电系统，其他为传统直流输电系统（LCC-HVDC）。

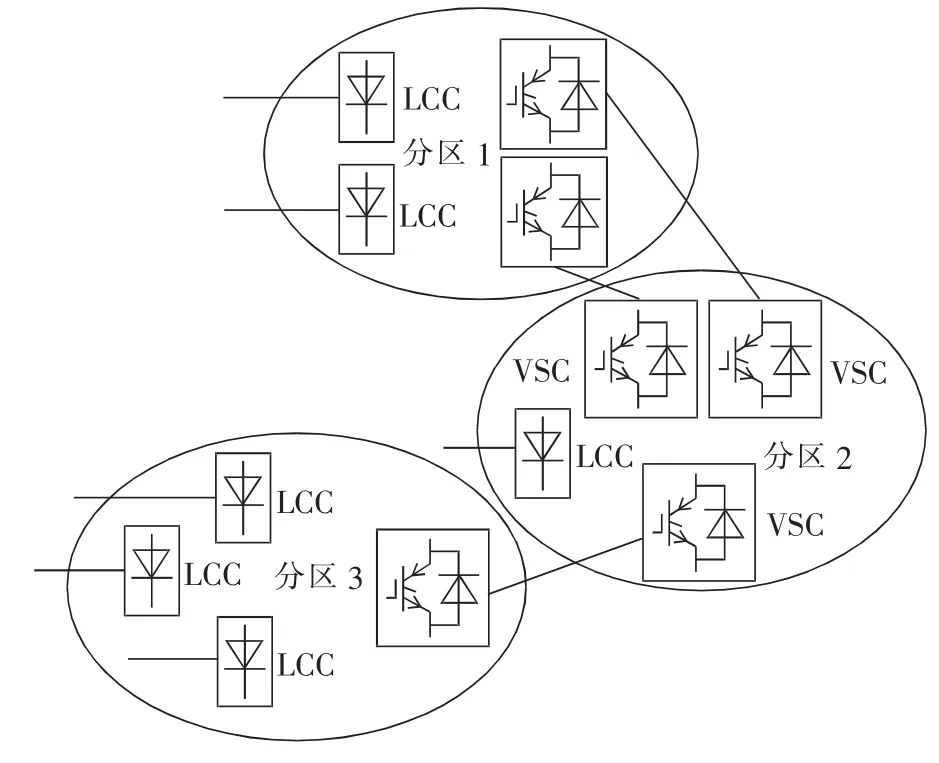
图1 多直流落点系统静态分区Fig.1 Static segmentation of multi-infeed HVDC system

利用电网静态分区技术对多直流落点系统进行分区能有效提升受端系统的运行性能。首先，静态分区将故障的影响范围限制在分区之内，避免了连锁故障引起的大面积停电，有效减少了故障下发生换相失败的直流系统数目；其次，柔性直流输电系统能够控制分区之间的潮流交换，有利于电能交易；再次，电网静态分区能够降低受端电网的短路电流水平。

2 稳定性问题及静态分区评价指标

本节从多直流落点系统常见的3个稳定性问题的角度分析静态分区方案对受端系统稳定性能的影响，阐述选择最优静态分区方案的必要性，并基于系统的稳定性问题提出静态分区方案的评价指标。

2.1 多直流落点系统稳定性问题

2.1.1 多直流发生换相失败问题

超多直流输电线路馈入同一受端系统，在受端系统短路故障下极有可能多条直流线路同时发生换相失败。如果直流系统送入功率大，将造成受端系统功率缺额过大，可能导致系统失稳。因此，故障下受端系统发生换相失败的直流线路数目越少，造成的功率缺额越小，系统的稳定性越好。

静态分区能够将故障限制在分区内，减少发生换相失败的直流线路的数目，从而减小整个系统崩溃的可能性。另一方面，静态分区后，由于分区的系统强度减弱，分区内直流之间相互影响增强，不利于防止多直流发生换相失败问题。因此，有必要对最优的静态分区方案进行选择。

从物理意义上讲，静态分区改变了直流落点之间的电气距离，本文采用多直流落点相互作用因子MIIF（Multi-Infeed Interaction Factor）来反映直流落点之间的耦合程度，从而评价静态分区方案对于多条直流线路同时发生换相失败问题的改善作用。

2.1.2 直流换相失败后系统恢复问题

多直流换相失败后，巨大的直流功率缺额和直流换流站恢复过程中大量的无功功率需求可能导致交流系统电压无法恢复，导致系统失稳。此外，系统低电压引起的自并励励磁系统励磁能力受限、交流线路无功损耗激增也进一步恶化了故障后交流系统的恢复过程。直流系统输送功率的快速恢复有助于受端系统的恢复，而直流换流母线电压支撑强度越大，直流系统功率的恢复能力越强，系统稳定性越好。

电网静态分区后，换流站所处的分区相比于分隔之前的受端系统强度下降，换流母线的电压支撑强度下降；另外，分区的大小对于换流母线的电压支撑强度也有影响。不同的静态分区方案对换流母线电压支撑强度的影响不同，因此有必要对其进行分析，选择影响程度较小的方案。

本文采用多直流落点有效短路比MIESCR（Multi-Infeed Effective Short Circuit Ratio）来衡量不同分区方案中各个分区出现直流换相失败后交流系统的恢复能力。

2.1.3 直流闭锁问题

直流线路输送功率较大，单回或多回直流闭锁将使得受端系统损失大量有功功率，分区频率下降，严重情况下会导致系统失稳。从稳定性角度分析，单回或多回直流闭锁后，分区频率支撑强度越强，分区频率偏差越小，系统稳定性越好。

不同静态分区方案各个分区的频率支撑强度不同，整个受端系统的频率稳定性也发生改变；同时电网静态分区后各个分区内电源数量相比于整个受端系统减少，相应的频率支撑强度减弱，因此有必要对最优静态分区方案进行研究和选择。

本文采用频率偏差因子以反映分区的频率支撑强度，从而评价电网静态分区后系统对于直流线路闭锁带来的安全稳定性问题的抵御作用。

2.2 静态分区方案评价指标

本文提出多直流落点相互作用因子、多直流落点有效短路比和频率偏差因子作为选择静态分区方案的评价指标，以反映多直流落点系统的稳定性。对于实际电网，若有较多个静态分区方案，如果通过暂态仿真检验各方案中受端系统各方面的稳定性能，则过程繁琐、计算量大、耗时长。而以上3个指标容易求得、计算工作量小，基于此可快捷地得到最优静态分区方案，有助于实际工程方案的选择。

2.2.1 多直流落点相互作用因子

CIGRE B4.41工作组［19］对多直流落点相互作用因子IMIIFfe的定义如下：

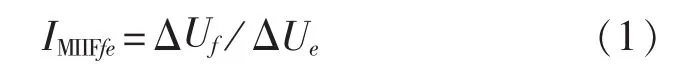
其中，ΔUe为换流站e交流母线上电压的自扰动量，约为1%；ΔUf为引起的换流站f交流母线的电压变化量。

IMIIF反映了换流站之间的电气距离，IMIIF越小，换流站之间电气耦合程度越低，受端系统在同一故障下同时发生换相失败的直流线路数目有可能减少。IMIIF是对换流站之间电气距离的度量，该值的大小从系统抵御多个换流站同时发生换相失败能力的角度表征了系统稳定性。

为了整体评价多直流落点系统换流站之间的耦合程度，引入多直流落点相互作用因子评价指标的计算值 FMIIFi，如式（2）所示，t为换流站的个数，FMIIFi反映了第i个静态分区方案中换流站之间的平均电气距离。

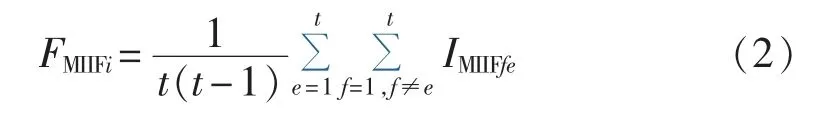
2.2.2 多直流落点有效短路比

多直流落点系统第e个换流站的短路比定义如式（3）所示，其中 Sace、Pdce（Pdcf）分别为换流站 e 交流母线短路容量和换流站e（f）的直流功率，Qce为换流站e内交流滤波器和并联电容器所提供的无功功率。

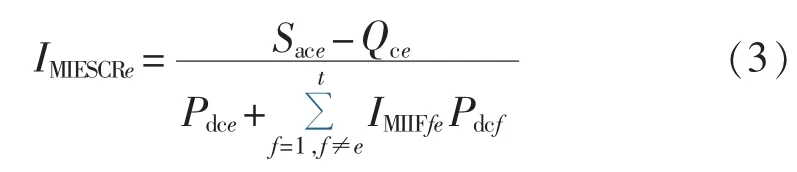
IMIESCR反映了交流电网对直流换流站的电压支撑水平，IMIESCR越大，直流换相失败后系统对换流母线的电压支撑强度越大，直流传输功率恢复越迅速，有利于受端系统的恢复过程。此外，IMIESCR的大小对直流最大功率运行点、动态过电压以及谐波谐振也有影响［20］。多直流落点有效短路比评价指标从直流换相失败后交流系统的恢复能力角度表征了系统稳定性。

在某个方案下对所有换流站的IMIESCR取平均值，从而反映该方案下短路比的整体情况，作为子指标 μ1，如式（4）所示。

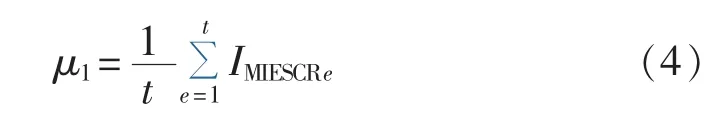
为了避免某些换流站IMIESCR过小对系统稳定性的影响，引入子指标μ2，即各换流站 IMIESCR的标准差，反映各值的均衡性，如式（5）所示。

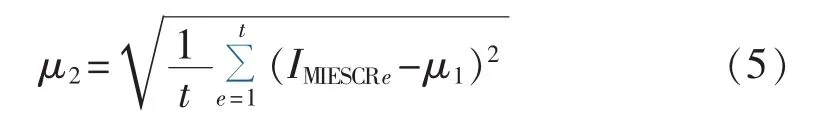
综合子指标μ1和μ2，通过线性加权和模型，可得第i个方案多直流落点有效短路比评价指标的计算值FMIESCRi。

2.2.3 频率偏差因子

频率偏差因子Iβg的定义如式（6）所示。其中Reqg为分区g内所有发电机的等效速度变动率，Dg为分区g内有功负荷的频率调节系数。

在静态分区方案中，由于送端与受端异步运行，因此必须考虑直流线路闭锁对送端系统和受端系统频率的影响。频率偏差因子评价指标能衡量受端系统频率的支撑强度。该因子的单位是MW／0.1Hz，即分区频率下降0.1Hz时，分区所失去的有功功率值。显然，频率偏差因子越大，表示分区的频率支撑强度越强，单回或多回直流闭锁情况下系统具有更大的稳定性。频率偏差因子从直流闭锁后交流系统的频率支撑强度角度表征了系统的稳定性。

采用各分区频率偏差因子平均值和标准差作为综合考量该指标的子指标，分别如式（7）和式（8）所示，p为静态分区数目。

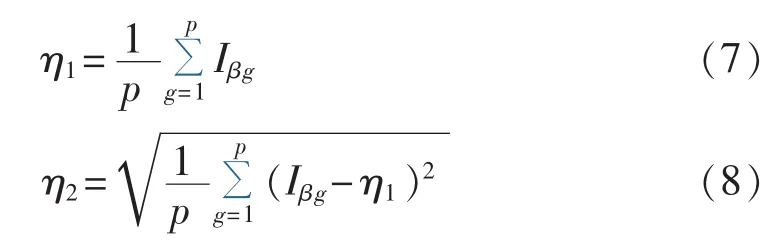
电网静态分区的最优方案应当是各分区的总体频率支撑强度较强，即η1较大；同时不期望出现某个分区频率支撑强度很弱的情况，各分区指标的偏差应当较小，即η2较小。综合以上2个子指标可计算出第i个方案的频率偏差因子评价指标值Fβi。

3 线性加权和模型

对于一个工程方案的评价，如果需要考虑多方面因素的影响，线性加权和法可对各个评价指标进行统一分析，最终得到各个方案的定量分析结果，根据结果可以对总体设计方案形成判断和选择。线性加权和模型在本文中用于：由子指标（μ1／μ2和η1／η2）计算对应的评价指标值（FMIESCR和 Fβ）；由评价指标值（FMIIF、FMIESCR和 Fβ）计算各方案的评价值。

3.1 模型概述

假设有n个静态分区方案，对每个方案有m个指标，则指标矩阵如式（9）所示。Rij表示第i个静态分区方案中第j个指标的数值。

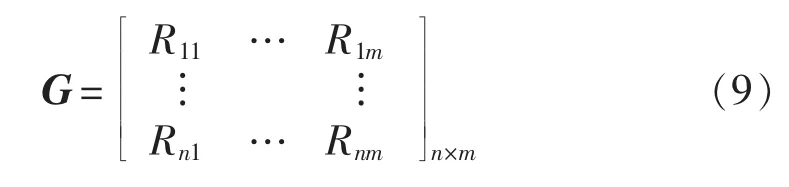
在多指标决策过程中，各个指标的单位或者数量级的差别会使决策产生偏差，影响决策结果，因此需要对各个指标进行归一化处理。归一化后的指标矩阵如式（10）所示。

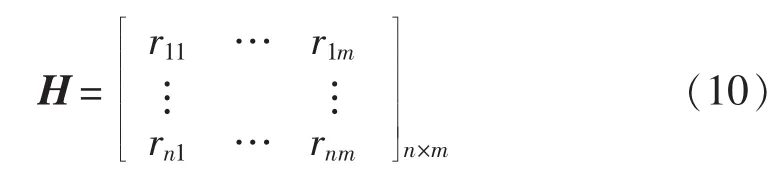
归一化后的指标rij落在区间［0，1］内。若rij=1，则第i个方案在第j个指标上表现最佳；若rij=0，则情况相反。下面阐述归一化方法。

对于第j个指标，Rjmax和Rjmin分别为该指标在所有静态分区方案中的最大值和最小值，如式（11）和式（12）所示。

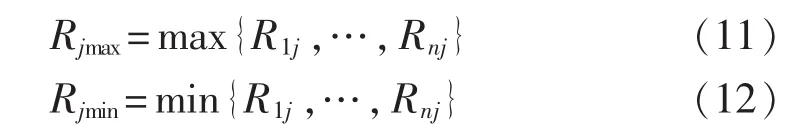
分2种情况进行归一化处理。

a.若某个指标越大，系统稳定性能越好（μ1或η1），归一化公式如式（13）所示。

b.若某个指标越小，系统稳定性能越好（FMIIF），归一化公式如式（14）所示。

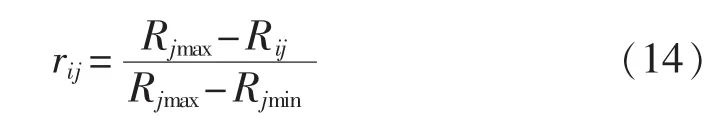
归一化后利用线性加权和模型对评价指标值或方案的评价值进行计算，如式（15）所示，Si为对第i种方案的评估数值，ωj为第j个指标的权重系数。对于各个候选方案，该模型的优化目标是找到一种方案，使得式（15）中的计算值Si尽可能大。

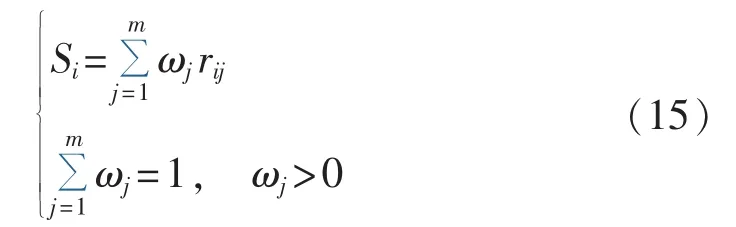
3.2 权重系数的确定

本文采用结合主观赋权法和客观赋权法的综合赋权法来确定权重系数。该方法通过主观赋权法和客观赋权法分别求出对应的权重系数，再利用综合赋权法得到最终的权重系数。主观赋权法依据对各个指标的重视程度进行赋权，而客观赋权法依据计算得到各方案的各个指标值确定权重系数，通过综合赋权法将两者结合起来，权重系数更能有助于最优方案的选择。

3.2.1 主观权重系数

根据2个指标（第j个和第w个）之间主观上的重要程度，可以得到两者之间的相对权重λjw和λwj，且满足 λjw+λwj=1（j≠ w）。 如果主观上第 j个指标比第w个指标更重要，则λjw＞λwj（例如λjw=60%，λwj=40%）。若有m个指标，可得到m×m阶的相对权重矩阵，如式（16）所示，其中 λjj=0（j=1，2，…，m）。

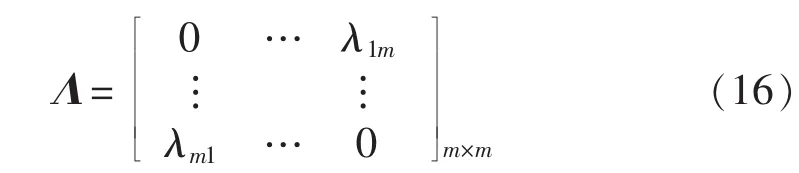
根据式（17），即可由主观赋权法得到各个指标的权重系数 ω′j。

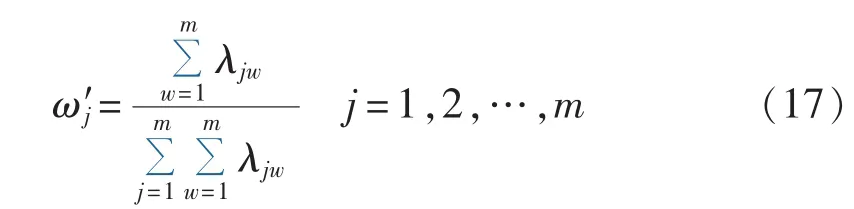
3.2.2 客观权重系数

本文根据指标的值在各方案中的变化程度确定客观赋权法对应的权重系数，若变化程度越大，则相应权重也越大。每个指标对应的反映指标值变化程度的变化系数如式（18）所示。

其中和σj分别为第j个指标在所有方案中的平均值和标准差。

根据式（19）可由客观赋权法计算得到各个指标的权重系数 ω″j。

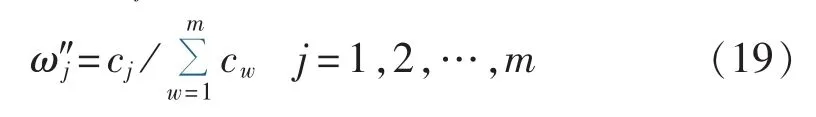
3.2.3 综合权重系数

综合赋权法考虑由主观权重确定的加权属性值和客观权重确定的加权属性值趋于一致，将主观赋权法得到的ω′j和客观赋权法得到的ω″j结合起来，如式（20）所示。

式（20）中的权重系数 a和 b由式（21）确定，其中a+b=1。

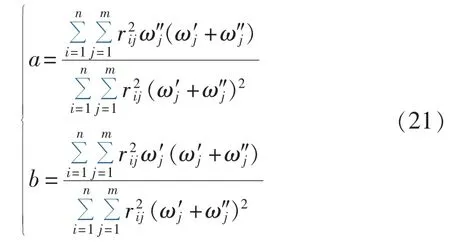
综合赋权法以客观赋权法为基础，同时通过主观赋权法对各个指标的权重有所侧重，因此综合赋权法结合了主客观赋权法的特点。

至此，本文建立了权重系数的计算方法，从而可确定由2个子指标值得到评价指标值和由3个评价指标值得到最终评价值过程中运用线性加权和模型的权重系数。

4 方案选择流程

静态分区方案的选择流程分以下4步。

a.计算各静态分区方案下多直流落点相互作用因子、多直流落点有效短路比和频率偏差因子。

b.分别计算多直流落点有效短路比和频率偏差因子在 n 个方案下的 2 个子指标（μ1／μ2和 η1／η2），并进行归一化处理，得到归一化子指标矩阵。

c.通过综合赋权法计算2个子指标的权重系数，利用线性加权和模型（式（15））得到n个方案下相应的评价指标值（FMIESCR和 Fβ）。 结合 FMIIF，得到归一化后的评价指标矩阵。

d.运用综合赋权法计算以上3个评价指标值的权重系数，同样利用线性加权和模型（式（15））得到各个方案下最终评价值S。选择S值最大的方案作为最终的静态分区方案。

综上，电网静态分区方案选择方法流程见图2。

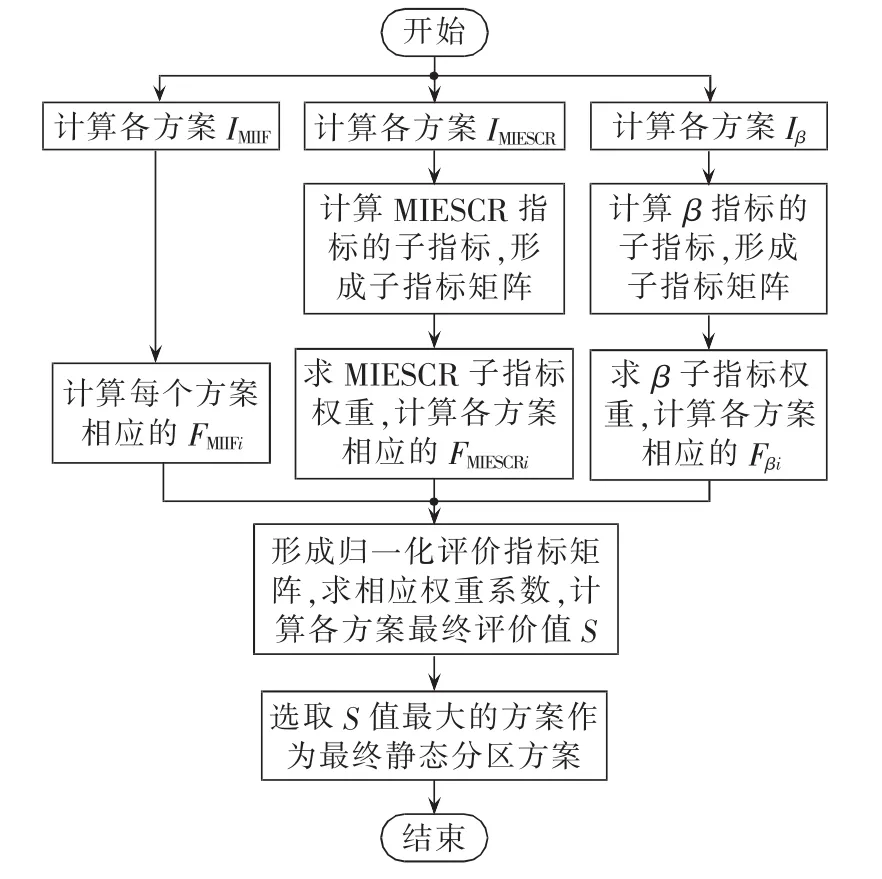
图2 选择方法流程图Fig.2 Flowchart of scheme selection

5 方案选择算例

本文以2030年广东电网规划网架为基础，各直流落点如图3所示。

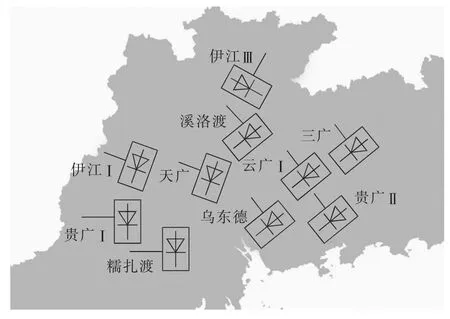
图3 2030年广东电网规划网架直流落点Fig.3 Locations of DC terminal planed for 2030’s Guangdong Grid

在各个候选方案中，每个异步分区包含的直流换流站如表1所示。

表1 静态分区方案Table 1 Static segmentation schemes

算例中将广东电网分隔成异步运行的2个分区，方案1、2和3为东西分区方案，方案4为南北分区方案，其中方案1和2各个分区内换流站相同，而柔性直流输电系统加装的位置不同。

5.1 方案选择

首先计算各方案对应 IMIIF、IMIESCR和 Iβ的值，并计算后2个评价指标的平均值子指标和标准差子指标，如表2所示。

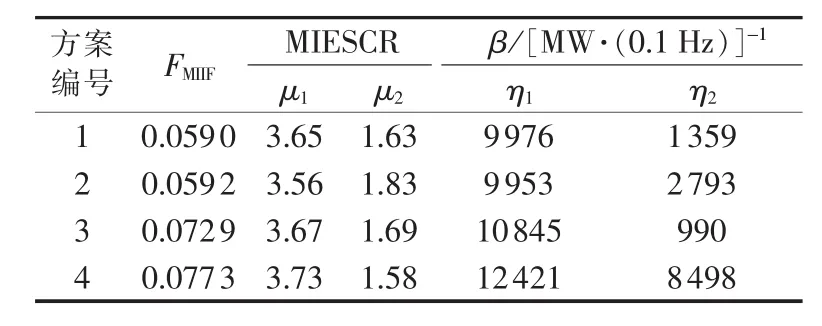
表2 各评价指标数值Table 2 Calculated values of evaluation indexes

对以上指标归一化处理，运用综合赋权法求出相应子指标的权重系数。并运用线性加权和模型得到每个方案中归一化后的各个评价指标值。

其次采用综合赋权法计算各个评价指标对应的线性加权和模型的权重系数。其中主观赋权法的相对权重矩阵如表3所示。

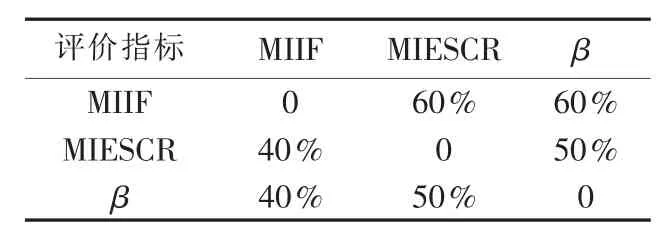
表3 主观赋权法相对权重矩阵Table 3 Relative weight matrix of subjective weight assignment method

表3考虑了多直流落点系统稳定性问题的轻重缓急，多直流发生换相失败对系统稳定性影响较大，在本方案中该稳定性问题权重相对较大，换相失败后系统的恢复问题和直流闭锁问题次之，总体上三者的权重系数相近。由主观赋权法和客观赋权法得到的权重系数ω′和ω″，以及结合两者得到的综合赋权法的权重系数ω如表4所示。

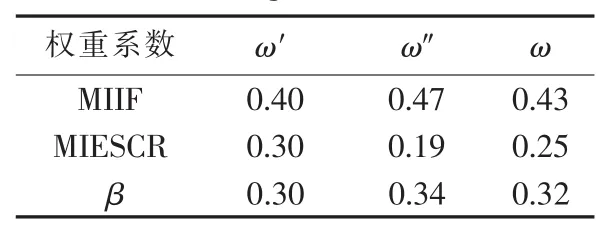
表4 权重系数表Table 4 Weight coefficients

最后，通过权重系数ω和归一化评价指标，依据式（15）计算各个方案的评估数值S，如表5所示。

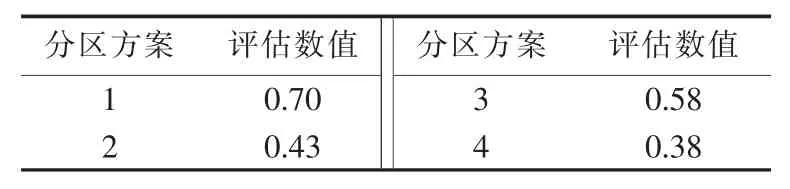
表5 各方案评估数值Table 5 Evaluation result for different schemes

由表5可见，采用本文静态分区方案的选择方法得到的各方案的评估数值排序为：S1＞S3>S2>S4。因此方案1为最优的分区方案。

5.2 仿真验证

考虑第2节提到的多直流落点系统的稳定性问题，即多直流发生换相失败问题、直流换相失败后系统恢复问题以及直流闭锁问题，基于PSS／E仿真软件，分别对各个方案在以上稳定性问题上的表现性能进行仿真。

a.针对多直流发生换相失败问题。对于每个方案，系统运行至1.0s时，在换流站换流母线上施加三相短路故障，1.1s时故障切除，观察系统发生换相失败换流站的个数。每条换流母线依次施加故障，统计每个故障下发生换相失败的换流站的平均个数。

b.针对直流换相失败后系统恢复问题。对于每个方案，系统运行至1.0s时，在换流站换流母线上施加三相短路故障，1.1 s时故障切除，记录该换流站功率恢复的时间。每条换流母线依次施加故障，统计各故障下对应换流站功率的平均恢复时间。

c.针对直流闭锁问题。对于每个方案，系统运行至1.0s时，直流线路单极闭锁，观察分区内频率的下降值。每条直流线路依次发生单极闭锁，统计每条直流单极闭锁后各分区频率的平均下降值。

对各个方案在以上3个稳定性问题上的表现性能分别进行仿真计算，结果如表6所示，其中括号中数字代表各方案的优劣排序。

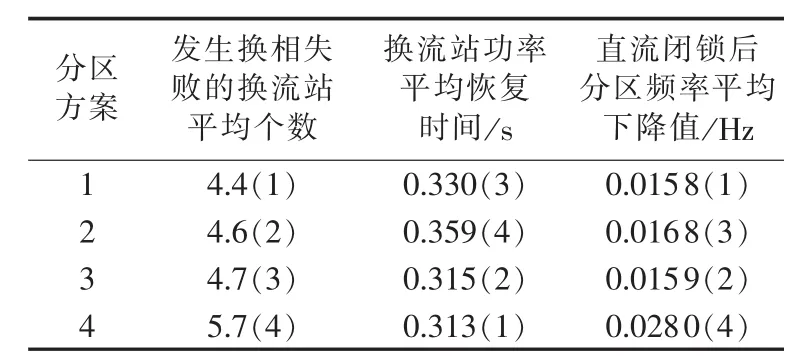
表6 各方案仿真结果Table 6 Simulative results for different schemes

从表6可以看出，方案1在抵御多直流同时发生换相失败和直流闭锁后频率支撑的性能表现上都是最好的，尽管换流站功率平均恢复时间不是最优的，但是平均恢复时间最短的方案4在另外两方面的稳定性能表现均存在明显不足。因此，通过仿真可以得到，方案1在以上三方面的稳定性问题上综合表现最优，与本算例中通过静态分区方案的选择方法得到的结果一致。

6 结论

a.本文分析了影响多直流落点受端系统安全稳定运行的3个问题和选择最优静态分区方案的必要性，在此基础上提出了基于多直流落点系统稳定性的评价指标，即多直流落点相互作用因子、多直流落点有效短路比和频率偏差因子，以及反映各个指标整体性和均衡性的子指标。

b.本文运用线性加权和模型求解静态分区方案选择的多目标决策问题，利用综合赋权法确定权重系数，建立了基于多直流落点系统稳定性的电网静态分区方案选择方法。

c.本文使用提出的方法对实际电网的静态分区方案进行选择，并对各方案的系统稳定性进行仿真，结果表明，静态分区方案选择方法得到的各方案优劣排序与系统稳定性仿真得到的各方案优劣排序具有一致性。

参考文献：

［1］邵瑶，汤勇.采用多馈入交互作用因子判断高压直流系统换相失败的方法［J］.中国电机工程学报，2012，32（4）：108-114.SHAO Yao，TANG Yong.A commutation failure detection method for HVDC systems based on multi-infeed interaction factors［J］.Proceedings of the CSEE，2012，32（4）：108-114.

［2］林凌雪，张尧，钟庆，等.多馈入直流输电系统中换相失败研究综述［J］.电网技术，2006，30（17）：40-46.LIN Lingxue，ZHANG Yao，ZHONG Qing，etal.A survey on commutation failure in multi-infeed HVDC transmission systerms［J］.Power System Technology，2006，30（17）：40-46.

［3］徐政.交直流电力系统动态行为分析 ［M］.北京：机械工业出版社，2004：1-6.

［4］HUANG H，XU Z，LIN X.Improving performance of multi-infeed HVDC systems using grid dynamic segmentation technique based on fault current limiters［J］.IEEE Transactions on Power Systems，2012，27（3）：1664-1672.

［5］WU J，WEN J，SUN H，et al.Feasibility study of segmenting large power system interconnections with ac link using energy storage technology［J］.IEEE Transactions on Power Systems，2012，27（3）：1245-1252.

［6］袁阳，卫志农，王华伟，等.基于直流电流预测控制的换相失败预防方法［J］.电网技术，2014，38（3）：565-570.YUAN Yang，WEI Zhinong，WANG Huawei，et al.A DC current predictive controlbased method to decrease probability of commutation failure ［J］.Power System Technology，2014，38（3）：565-570.

［7］HANSEN A，HAVEMANN H.Decreasing the commutation failure frequency in HVDC transmission systems［J］.IEEE Transactions on Power Delivery，2000，15（3）：1022-1026.

［8］CLARK H，EDRIS A A，EL-GASSEIR M，et al.Softening the blow of disturbances［J］.Power and Energy Magazine，IEEE，2008，6（1）：30-41.

［9］FANG Xinghao，CHOW J H.BTB DC link modeling，control，and application in the segmentation of AC interconnections［C］∥2009 IEEE Power&Energy Society General Meeting.Calgary，AB，Canada：IEEE，2009：1-7.

［10］CHANG Y C.Multi-objective optimal SVC installation for power system loading margin improvement［J］.IEEE Transactions on Power Systems，2012，27（2）：984-992.

［11］李如琦，李芝荣，王维志，等.基于差分策略的多目标电力系统无功优化［J］.电网技术，2012，36（12）：170-175.LI Ruqi，LI Zhirong，WANG Weizhi，et al.Multi-objective reactive power optimization based on difference strategy［J］.Power System Technology，2012，36（12）：170-175.

［12］刘述奎，李奇，陈维荣，等.改进粒子群优化算法在电力系统多目标无功优化中应用［J］.电力自动化设备，2009，29（11）：31-36.LIU Shukui，LI Qi，CHEN Weirong，et al.Multiobjective reactive power optimization based on modified particle swarm optimization algorithm［J］.Electric Power Automation Equipment，2009，29（11）：31-36.

［13］CHEN Y L.Weak bus-oriented optimal multi-objective var planning［J］.IEEE Transactions on Power Systems，1996，11（4）：1885-1890.

［14］栗然，马慧卓，祝晋尧，等.分布式电源接入配电网多目标优化规划［J］. 电力自动化设备，2014，34（1）：6-13.LI Ran，MA Huizhuo，ZHU Jinyao，et al.Multi-objective optimization for DG integration into distribution system［J］.Electric Power Automation Equipment，2014，34（1）：6-13.

［15］邱威，张建华，刘念.电压稳定约束下最优潮流的多目标优化与决策［J］.电力自动化设备，2011，31（5）：34-38.QIU Wei，ZHANG Jianhua，LIU Nian.Multi-objective optimization and decision making of voltage stability constrained optimal power flow［J］.Electric Power Automation Equipment，2011，31（5）：34-38.

［16］王康，刘崇茹，韩民晓，等.兼顾稳定性与经济性的交直流系统直流落点选择方法［J］.电力系统自动化，2011，35（24）：73-78.WANG Kang，LIU Chongru，HAN Minxiao，et al.A method of selectingDC linkstermination atAC locationsconsidering stability and economy at once［J］.Automation of Electric Power Systems，2011，35 （24）：73-78.

［17］陆文玲，吴杰康.水火电力系统短期优化调度的多目标决策评价方法［J］.中国电机工程学报，2011，31（增刊 1）：23-29.LU Wenling，WU Jiekang.Multi-objective decision based methods for short-term optimal scheduling of hydrothermal electric power systems［J］.Proceedings of the CSEE，2011，31（Supplement 1）：23-29.

［18］胡运权.运筹学教程［M］.北京：清华大学出版社，2007：426-430.

［19］CIGRE Working Group B4.41.Systems with multiple DC infeed［R］.Paris，France：CIGRE，2008.

［20］林伟芳，汤涌，卜广全.多馈入交直流系统短路比的定义和应用［J］.中国电机工程学报，2008，28（31）：1-8.LIN Weifang，TANG Yong，BU Guangquan.Definition and application of short circuit ratio for multi-infeed AC／DC power systems［J］.Proceedings of the CSEE，2008，28（31）：1-8.