基于单向S-粗集理论的输电系统可靠性评估
杨晓萍 ,王 媛 ,王 明 ,2
(1.西安理工大学 水利水电学院,陕西 西安 710048;2.国电南京自动化股份有限公司,江苏 南京 210032)
0 引言
近年来,天气情况对电力系统运行的影响越来越受到关注。暴风、雷雨、覆冰等偶发性天气均会影响元件的故障率[1-3],严重的大风、覆冰可能会造成倒塔,破坏基础设施[4-5],各种元件、设备的故障率突然增加还会造成电厂中大量机组相继切出[6-8],严重的天气变化事件会导致聚集性故障,对电力系统可靠运行危害极大。因此,研究不同天气条件对输电系统可靠性的影响非常必要,能够为电力系统的稳定运行提供关键信息。
电力系统可靠性评估方法是以元件可靠性原始参数为基础的。目前,输电系统可靠性计算多采用平均值作为元件可靠性参数,但这些参数随运行环境不同而差别很大,直接用平均值进行可靠性计算与实际情况误差较大。文献[9]根据电力系统可靠性原始参数的特点,在原始数据缺乏的情况下,利用灰色模型对输电线路故障率进行预测,该方法在面对大样本的情况下,精度略显不足。文献[10-11]根据经验公式对输电线路可靠性的影响因子进行分析,但影响因子的处理采用简单的数学相加,并不符合实际情况,不能反映气象因子的实际作用。文献[12]运用联系数建立故障率模型,考虑了天气对线路故障率的不确定性,但没有考虑实际的天气情况,与实际不符。
波兰数学家Z.Pawlak教授于1982年提出粗集理论,它是一种处理模糊和不确定知识的数学工具,能有效地分析和处理各种不精确、不一致、不完整的信息,并从中发现隐含的知识,揭示潜在的规律。粗集理论已在电力系统负荷预测[13]、电网规划[14]、故障选线[15]等方面得到了应用。史开泉教授在粗集理论的基础上,提出了用动态集合描述的单向、双向S粗集以及函数 S-粗集、F-分解规律[16]等理论。
由于可靠性评估常常会受到气候因素、地理因素等一些动态的、不确定的外部因素的影响,使得故障率和可靠性指标具有不确定性。单向S-粗集理论具有规律性和动态迁移性,能很好地解决此类具有动态特性的不确定规律问题。
本文针对现有可靠性评估方法的不足,基于历史统计数据,分析天气随机变化的特点,采用单向S-粗规律分析方法,建立考虑天气因素的元件可靠性参数模型,用F-分解规律分析气候对可靠性指标的影响程度,对输电线路故障率进行预测,优化输电系统可靠性评估方法,揭示天气因素对可靠性评估的影响规律。最后将本文采用的方法与常规方法的可靠性指标进行对比,验证本文方法的有效性、合理性。
1 单向S-粗集理论[17]
在电力系统可靠性评估中,当影响可靠性的外部因素不变时,其影响因子用属性集A描述,其对应的影响因子属性值为X,采用单向S-粗规律得到元件故障率模型,即元件故障率与影响因子之间的关系。当外部因素动态变化时,属性集A变为Af,属性值X变为Xf,采用F-分解粗规律分析可靠性指标与影响因子的关系。
1.1 单向S-粗规律
设 A 为规律 p(t)的属性集,X 为 p(t)的属性值向量,即 X= [x1,x2,…,xm]为属性集 A= {a1,a2,…,am}的值,其中m为属性的个数。利用元件故障率模型得到故障率集 λ={λ1,λ2,…,λn},n 为线路数,再通过规律生成模型,得到元件故障率的粗规律p(t)。
1.2 F-分解粗规律
在一个动态系统中,a为具有动态特性的属性集,以 f作为动态迁移族。 若 Af=A∪{a′}={a1,a2,…,am,a′},其中 a′为新增加(减少)的属性,则称 Af为 A 的属性补充集,同理 Xf=[x1,x2,…,xm,x′]为属性值向量 X 的 f-分解向量,从而 pf(t)为 p(t)的 f-分解规律。 称 p(t)为 p(t)的 F-上分解规律,p(t)为p(t)的 F-下分解规律,则称(p(t),p(t))为 F-分解粗规律。
2 考虑天气因素的元件可靠性参数模型
一些在户外运行的输电系统设备,特别是架空线路,受雷雨、冰雹、大雾等天气的影响很大,因此需要在多态天气下考虑元件的可靠性参数。
根据可靠性影响因子的特点,将影响架空输电线路故障率的因素归结为以下几类:暴风天气(a1);暴雨天气(a2);冰雪天气(a3);高温天气(a4);地基原因及其他(a5);投产时间(a6)。 其中 a1— a4为天气量,a5、a6为非天气量。则影响因子的属性集A={a1,a2,a3,a4,a5,a6},影 响 因 子 的 属 性 值 向 量 X=[x1,x2,x3,x4,x5,x6]。 设各种属性所对应的权重 H=[h1,h2,h3,h4,h5,h6]T,且有
2.1 元件故障率模型
如果电力系统输电线路数为n,则由各条线路属性值向量Xi得到属性特征值矩阵为:
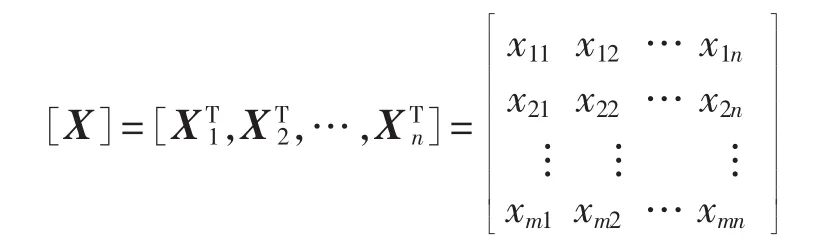
计算属性特征值矩阵中每个特征值xij的效益型目标优度:
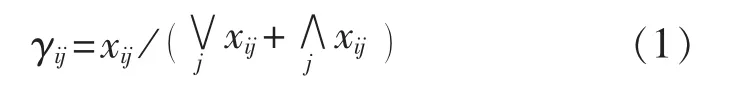
其中,∨为取大运算;∧为取小运算。
得到目标优度矩阵Γ为:
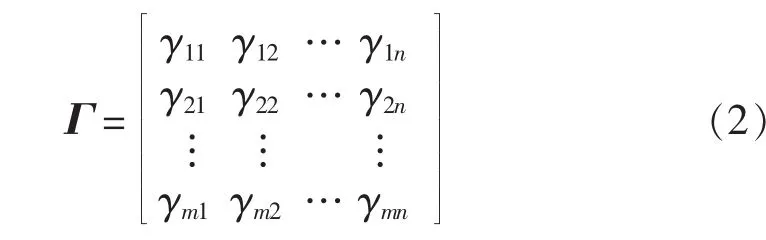
其中,γij为目标优度。
根据逼近于理想解的排序方法(TOPSIS),构筑理想优度(优等决策的目标优度)和负理想优度。
理想优度向量为:
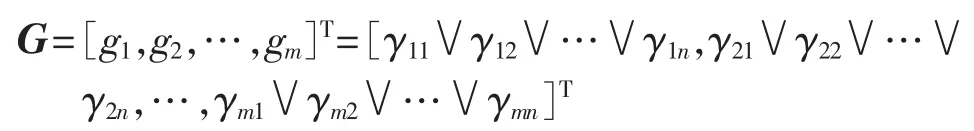
负理想优度向量为:
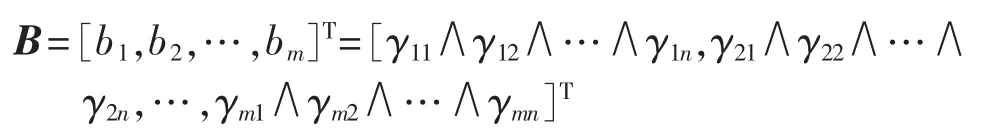
由各条线路的属性权重Hi得到权重矩阵为:
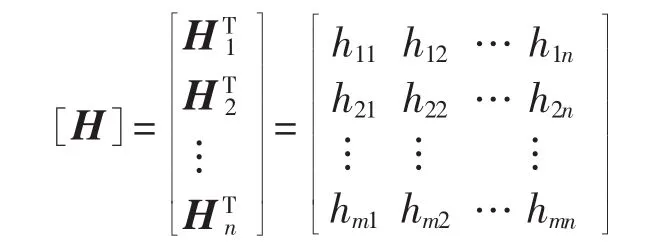
将权重矩阵中各权重值代入式(3)得到故障率λi:
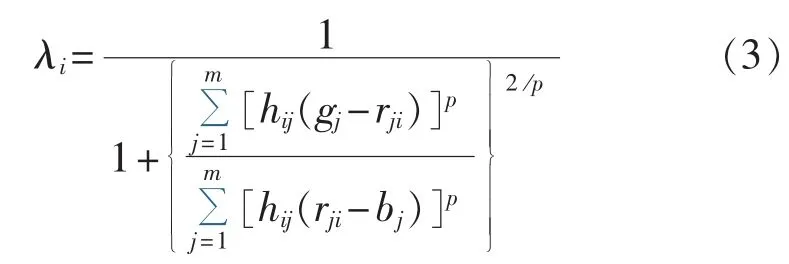
其中,i=1,2,…,n;j=1,2,…,m;距离参数 p=2。进而得到元件故障率集 λ={λ1,λ2,…,λn}。
当影响因子集A动态扩张时,形成了影响因子值序列集,即{X}={X}0⊇{X}1⊇{X}2⊇…⊇{X}k-1⊇{X}k时,将得到一个元件故障率序列集:
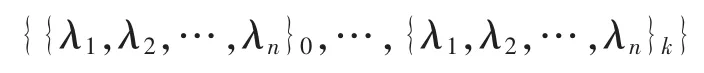
2.2 元件故障率的粗规律生成模型
元件故障率样本中天气量为变化因子,非天气量为相对稳定因子。所以以天气量作为单侧动态变化量,形成新的样本集{Xfi,λfi}。
将集合λ数据代入Lagrange插值式,得到集合λ的一种规律生成:
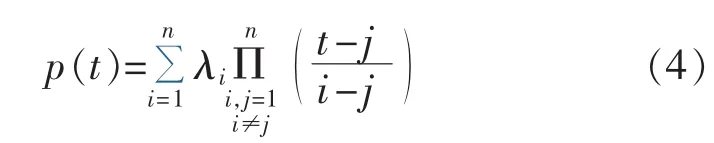
其中,t为线路编号。
考虑天气量与非天气量时,由式(3)形成λi,通过规律生成模型式(4)得到规律 p(t),形成上规律(t);只考虑非天气量时,形成 λfi,通过规律生成模型得到规律 pf(t),形成下规律 p(t)。 因此,形成单向S-粗规律
2.3 预测元件故障率
已知历年天气样本值,用正态抽样方法预测下一年的天气量。非天气量因为相对稳定,采用平均值确定下一年的非天气量。根据2.1节所述元件故障率模型,可以预测下一年的元件故障率λn+1。
3 可靠性评估流程
3.1 原始数据处理
首先根据故障率样本,预测各条线路故障率;其次,根据2.3节所述预测下一年的元件故障率λn+1;再用F-分解粗规律,根据不同的天气变化,得到不同的Xfi,进而得到不同天气情况下的故障率λfi。
3.2 系统状态选择
蒙特卡洛模拟法在复杂电网可靠性评估中得到了广泛的应用,由于非序贯蒙特卡洛法抽样简单且所需原始数据较少,故本文采用非序贯蒙特卡洛方法进行系统状态选取。
本文采用两状态模型,假设每个元件都只有故障和运行2种状态,并且元件的故障彼此独立。如果元件i的故障率和修复率分别为λi和μi,元件的强迫停运率则元件的状态为:

其中,si=0表示元件处于故障状态,si=1表示元件处于运行状态;ri为元件i在[0,1]区间内均匀分布的随机数。
那么具有d个元件的系统状态可表示为:
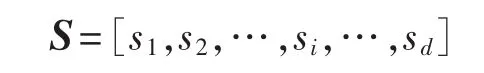
3.3 系统状态分析
采用非序贯蒙特卡洛法对系统所有元件进行状态选取之后,可能会使系统网络拓扑结构发生很大变化,所以需要进行网络拓扑分析。本文采用深度优先算法进行网络拓扑分析,判断系统是否解列,进而进行潮流分析,得到各节点的电压、线路有功和无功值等;再进行切负荷计算,得到系统可靠性指标计算所需数据。其中求解最小切负荷的数学模型采用文献[18]中最优负荷削减模型。
3.4 运行计算系统可靠性指标和能量规律、规律干扰度
3.4.1 系统可靠性指标计算
在系统状态选取和状态分析后,计算系统的可靠性指标。由系统可靠性指标计算公式[19]得到考虑天气变化的系统可靠性指标。
(1) 电力不足概率 LOLP(Loss Of Load Probability),即系统有效容量不能满足负荷要求的时间概率,又称为系统停电概率,可以用式(6)表示:

其中,Nfi为节点或者系统的停电次数;Ns为抽样次数。
(2) 功率不足期望值 EPNS(Expected Power of Not Supplied)可用式(7)表示:
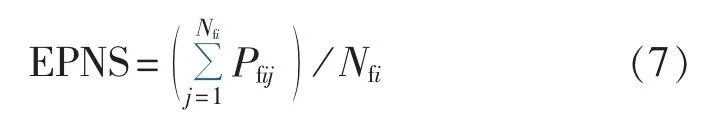
其中,Pfij为节点i在系统第j次抽样状态下的停电功率。
(3) 电量不足期望值 EENS(Expected Energy of Not Supplied),即在一定时期内由于供电不足而造成用户停电损失电量的期望值,可以用式(8)表示:

其中,Efij为节点i在系统第j次抽样状态下的停电电量。
3.4.2 规律能量和规律干扰度
规律能量是元件性能的反映,可以作为选择元件的依据。规律干扰度反映不同天气情况对输电系统的影响程度。
规律能量:设 p(t)为区间[a,b]上的规律,称 w为p(t)的规律能量,可表示为:

规律干扰度:设 pf(t)为分解基 p(t)生成的 f-分解规律,称 ρ为 pf(t)关于 p(t)的属性 f-扰动度,可表示为:
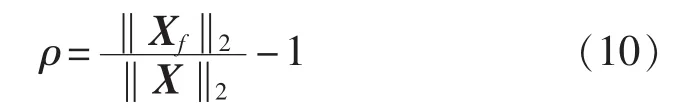
其中,X为p(t)对应的属性值向量,‖X‖2为向量X的2范数。
随着F-分解粗规律的干扰属性集的逐渐增加(减少),F-分解粗规律的干扰程度逐渐减弱(增强)、规律能量逐渐增大(减小);F-分解粗规律的干扰度描述了F-干扰对可靠性的影响程度。 如果(pF(t),pF(t))的 F-故障率粗规律干扰度(ρf,ρf)=0,则系统对p(t)的F-分解粗规律的干扰趋于平衡,F-干扰对p(t)不产生影响。
4 算例分析
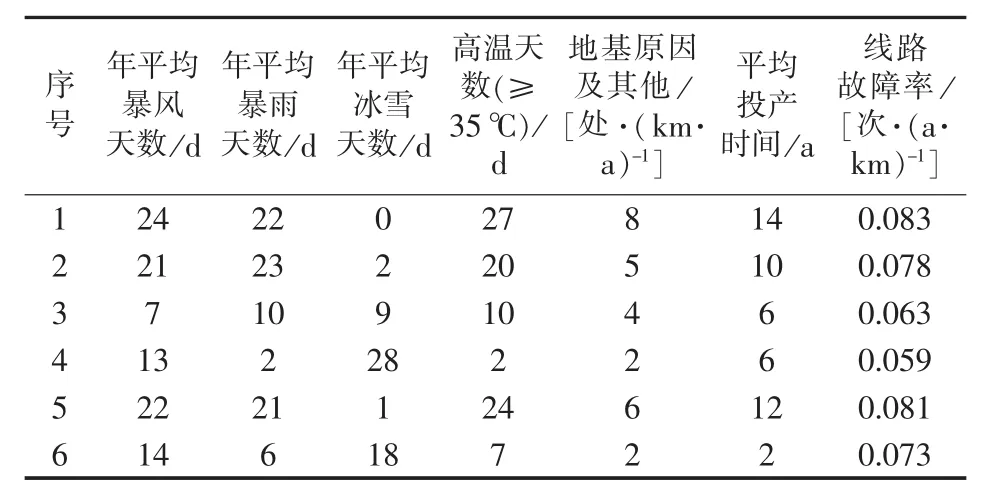
表1 各线路故障率及影响因素Table 1 Failure rate and influencing factors of different lines
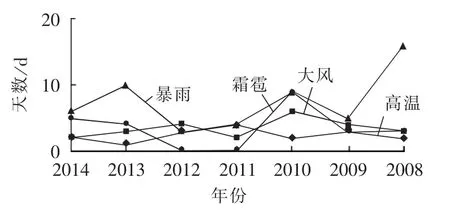
图1 历年天气Fig.1 Historical weather data
线路故障率样本数据见表1,2008—2014年的天气数据如图1所示。根据本文提出的模型算法,对IEEE30节点测试系统的可靠性进行评估。由于大部分输电线路在户外运行,特别是架空线路,受雷雨、冰雹、大雾等天气的影响特别大,而变压器受天气影响较小,因此在本文可靠性评估中,输电线路的故障率考虑天气影响的不确定性,而变压器的故障率则采用平均值[20]。
4.1 单向S-粗集预测合理性检验
首先,利用元件故障率粗规律生成模型预测表1中各线路的故障率规律p(t),即故障率λ的上、下范围值如图2所示,并与表1中输电线路实际值进行对比。
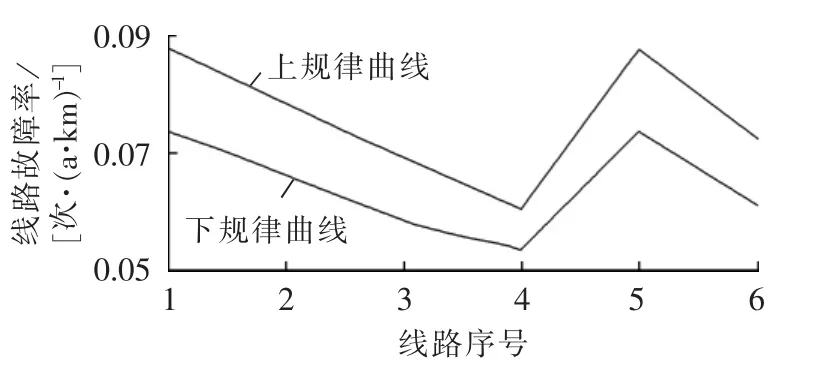
图2 S-粗规律对线路故障率的预测范围Fig.2 Range of line failure rate forecast by S-rough law
由图2和表1可以看出,输电线路故障率的实际值在用单向S-粗规律得出的上、下故障率规律范围内,证实了单向S-粗规律对输电线路故障率预估的合理性。
4.2 预测2015年线路故障率
根据如图1所示的历年天气样本值,采用正态抽样方法预测2015年的天气量。得到属性值向量X= [3.876 2,2.733 8,10.532 9,28.386,5,10],其中非天气量采用平均值。
由元件故障率模型、规律生成模型得出2015年的线路故障率λ的范围值为[0.061,0.073]。
4.3 可靠性评估
由2015年的线路故障率λ值的上、下限值,通过VC++编程对IEEE 30节点系统进行可靠性评估,得到可靠性指标 LOLP、EPNS、EENS的上、下限值。
表2中给出了不考虑天气情况影响即故障率为平均值(方法1)、考虑天气情况影响的可靠性评估方法[12](方法2)和本文方法的可靠性评估结果。
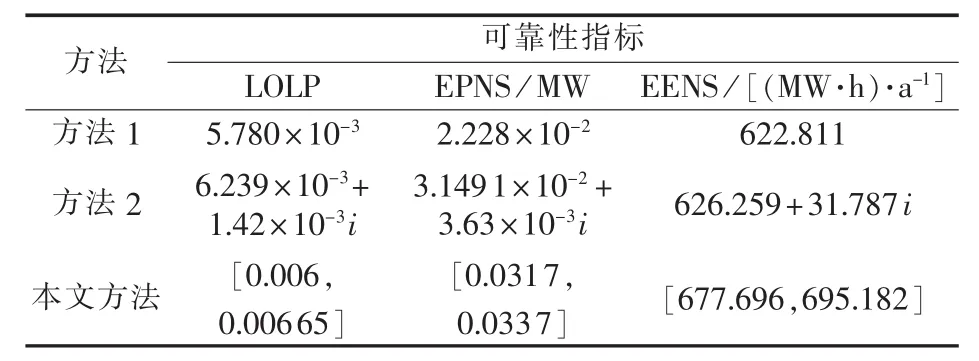
表2 可靠性评估对比Table 2 Comparison of reliability indices among evaluation methods
由表2可以看出,方法1和方法2结果之间存在偏差。而外界影响是可靠性评估时必须要考虑的因素,本文由已知的影响因素得出故障率的范围值,更符合实际情况。
方法2和本文方法的评估结果均为范围值,但方法2的范围值是通过对故障率以天气的不确定性取 ±10%,再以 i∈[-1,1]的随机取值来体现可靠性评估结果不确定性的动态波动;本文方法依据客观数据(天气情况)预测故障率λ的上、下范围值进行可靠性评估,更具客观性。
4.4 不同天气下可靠性评估影响分析
因为气候因素多为动态影响,在考虑综合因素的作用下,选取4种气候因子进行试验,运用F-分解规律分析不同天气下的可靠性指标,得到能量规律w和干扰度ρ值。根据w和ρ,分析天气对可靠性指标的影响,如表3所示。为了分析各种因素的影响程度,设置以下6种情况进行可靠性评估:情况1,acase1= {a1,a2,a3,a4,a5,a6};情况 2,acase2= {a4,a5,a6};情况 3,acase3={a3,a5,a6};情况 4,acase4={a2,a5,a6};情况5,acase5= {a1,a5,a6};情况 6,acase6= {a5,a6}。 其中,因素a1为暴风天气,a2为暴雨天气,a3为冰雪天气,a4为高温天气,a5为地基原因,a6为投产时间。
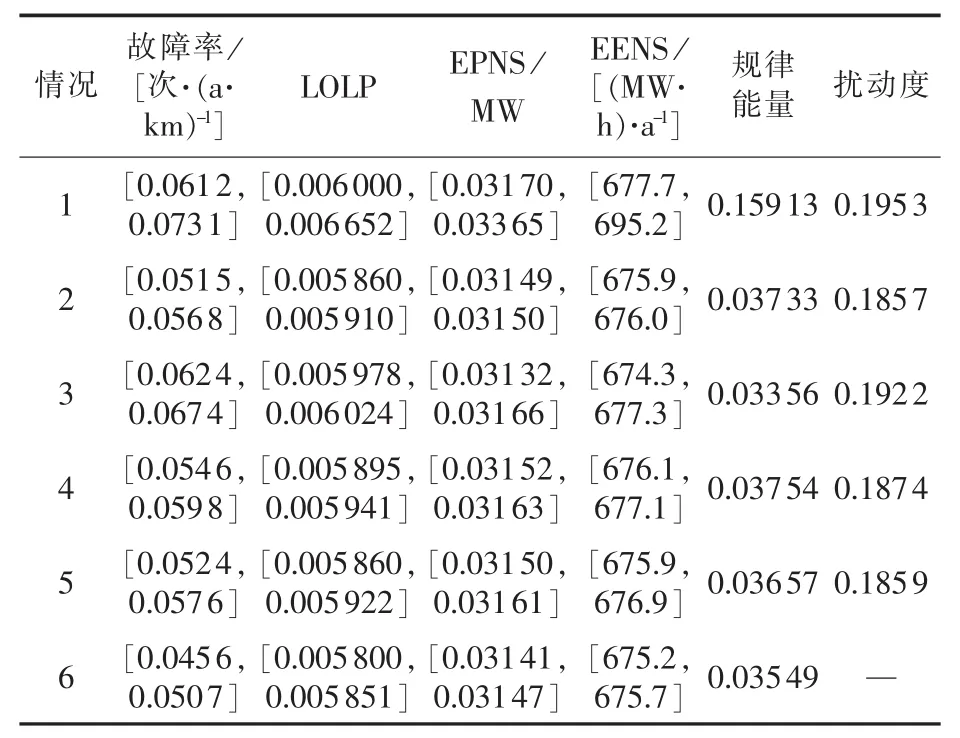
表3 不同天气组合下输电线路数据Table 3 Transmission line data of different weather conbinations
由表3可以看出,冰雪因子对可靠性指标影响最大,暴雨因子次之,高温因子与暴风因子对其影响程度相同,影响较小。从扰动度可看出,4种气候因子共同作用时,并不是单个因子简单地相加,而是复杂的多种天气因素综合作用的结果。从规律能量可以看出,影响因素越弱,规律能量越小,输电线路性能越好。可靠性指标范围越小,可靠性指标越精确。
5 结论
本文提出了不同天气下基于单向S-粗集的可靠性评估方法。运用单向S-粗集处理线路故障率和天气情况的不确定性,F-分解规律分析天气对可靠性指标的影响,对可靠性指标的不确定性有确定的度量。用单向S-粗集理论处理输电系统可靠性参数的不确定性只需要简单的年气候天数,由此得到的可靠性指标以客观数据为基础,可以杜绝人为主观因素的影响,评估结果更客观。
运用本文所提方法在IEEE 30节点仿真系统进行可靠性评估,结果如下。
(1)基于天气情况的不确定性,单向S-粗集可以合理地预测输电线路故障率。
(2)得到的可靠性指标反映了整个电力系统可靠性运行的实际情况,而扰动度指标则反映了天气对系统可靠性的影响程度。通过扰动度指标分析,可以揭示天气因素对系统可靠性的影响规律,对此,根据天气影响规律采取相应措施,提高系统可靠性及应对不利天气的能力。
参考文献:
[1]刘洋,周家启.计及气候因素的大电力系统可靠性评估[J].电力自动化设备,2003,23(9):60-62.LIU Yang,ZHOU Jiaqi.Incorporating weather effect in bulk power system reliability evaluation [J].Electric Power Automation Equipment,2003,23(9):60-62.
[2]李银华,韩郡业,王婷.架空电力线覆冰监测系统[J].电力自动化设备,2009,29(11):112-115.LI Yinhua,HAN Junye,WANG Ting.Ice monitoring system of overhead electrical power lines[J].Electric Power Automation Equipment,2009,29(11):112-115.
[3]李鹏,任震.广州电网负荷特性分析及短期预测模型设计[J].电力自动化设备,2002,22(8):50-53.LIPeng,REN Zhen.Guangzhou regionalload analysisand short-term forecasting model desig[J].Electric Power Automation Equipment,2002,22(8):50-53.
[4]唐斯庆,张弥,李建设,等.海南电网“9·26”大面积停电事故的分析与总结[J]. 电力系统自动化,2006,30(1):1-7,16.TANG Siqing,ZHANG Mi,LI Jianshe,et al.Review of blackout in Hainan on September 26th-cause and recommendations[J].Automation of Electric Power Systems,2006,30(1):1-7,16.
[5]庞准,李邦峰,俞悦,等.海南电网台风期间运行方式研究[J].电网技术,2007,31(7):46-50.PANG Zhun,LI Bangfeng,YU Yue,et al.Study on operating modes of Hainan power grid during typhoon periods[J].Power System Technology,2007,31(7):46-50.
[6]GREAVES B,COLLINS J,PARKES J,et al.Temporal forecast uncertainty for ramp events[J].Wind Engineering,2009,33(4):309-319.
[7]KAMATH C.Understanding wind ramp events through analysis of historical data[C]∥2010 IEEE PES Transmission and Distribution Conference and Exposition.New Orleans,LA,USA:IEEE,2010:1-6.
[8]ZAREIPOUR H,HUANG D,ROSEHART W.Wind power ramp events classification and forecasting:a data mining approach[C]∥ Power and Energy Society General Meeting.Michigan,USA:IEEE,2011:1-3.
[9]张勇军,袁德富,汪穗峰.基于模糊差异度的电力系统可靠性原始参数选取[J]. 电力自动化设备,2009,29(2):43-46.ZHANG Yongjun,YUAN Defu,WANG Suifeng.Selection of reliability original parameters in power system based on the fuzzy difference degree[J].Electric Power Automation Equipment,2009,29(2):43-46.
[10]朱益华,罗毅,段涛,等.基于输电线路实时评估模型的电力系统静态安全在线风险评估[J]. 电力自动化设备,2014,34(7):150-156.ZHU Yihua,LUO Yi,DUAN Tao,et al.Online risk assessment based on real-time evaluation model of transmission line for static security of power system [J].Electric Power Automation Equipment,2014,34(7):150-156.
[11]何剑,程林,孙元章,等.计及天气预测的电力系统运行可靠性短期评估[J]. 电力系统保护与控制,2010,38(10):31-38.HE Jian,CHENG Lin,SUN Yuanzhang,etal.Powersystem short-term operational reliability evaluation considering weather forecast[J].Power System Protection and Control,2010,38(10):31-38.
[12]王磊,赵书强,张明文.考虑天气变化的输电系统可靠性评估[J].电网技术,2011,35(7):66-70.WANG Lei,ZHAO Shuqiang,ZHANG Mingwen.Reliability evaluation oftransmission system consideringweatherchange [J].Power System Technology,2011,35(7):66-70.
[13]牛东晓,王建军,李莉,等.基于粗糙集和决策树的自适应神经网络短期负荷预测方法[J]. 电力自动化设备,2009,29(10):30-34.NIU Dongxiao,WANG Jianjun,LILi,etal.Short-term load forecasting using adaptive ANN based on rough setand decision tree[J].Electric Power Automation Equipment,2009,29(10):30-34.
[14]刘思革,程浩忠,崔文佳.基于粗糙集理论的多目标电网规划最优化模型[J]. 中国电机工程学报,2007,27(7):65-69.LIU Sige,CHENG Haozhong,CUI Wenjia.Optimal model of multi-objective electric power network planning based on rough set theory[J].Proceedings of the CSEE,2007,27(7):65-69.
[15]庞清乐,孙同景,钟麦英,等.基于粗集理论的小电流接地系统故障选线[J]. 中国电机工程学报,2007,27(4):60-64.PANG Qingle,SUN Tongjing,ZHONG Maiying,et al.Fault line detection based on rough set theory in indirectly grounding power system[J].Proceedings of the CSEE,2007,27(4):60-64.
[16]黄顺亮,史开泉.粗规律能量与F-分解粗规律度量[J].计算机科学,2009,36(1):177-180.HUANG Shunliang,SHI Kaiquan.Rough law energy and F-decomposing rough law measurement[J].Computer Science,2009,36(1):177-180.
[17]黄顺亮,史开泉.单向S-粗决策规律与决策规律挖掘[J].系统工程与电子技术,2008,30(5):858-862.HUANG Shunliang,SHI Kaiquan. One direction S-rough decision law and decision law mining[J].Systems Engineering and Electronics,2008,30(5):858-862.
[18]赵渊,周家启,刘洋.发输电组合系统可靠性评估中的最优负荷削减模型分析[J]. 电网技术,2004,28(10):34-37.ZHAO Yuan,ZHOU Jiaqi,LIU Yang.Analysis on optimal load shedding model in reliability evaluation of composite generation and transmission system[J].Power System Technology,2004,28(10):34-37.
[19]宋晓通,谭震宇.大型发输电组合系统可靠性评估方法[J].高电压技术,2007,33(7):191-194.SONG Xiaotong,TAN Zhenyu. Methodology for reliability evaluation of bulk composite generation-transmission system[J].High Voltage Engineering,2007,33(7):191-194.
[20]BILLINTON R,KUMAR S,CHOWDHURY N,et al.A reliability test system for educational purposes-basic data[J].IEEE Transactions on Power Systems,1989,4(3):1238-1244.

