基于可观测量的同步发电机模型参数的频域辨识

陆晓依 ，罗 建，姚志良 ，曾伟章

（1.重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400040；2.广东电网有限责任公司东莞供电局，广东 东莞 523000）

0 引言

同步发电机作为电力系统中的重要设备之一，其模型和参数是电力系统运行控制分析的基础［1-2］。

同步发电机参数辨识方法可以分为离线辨识和在线辨识2类。离线辨识一般在发电机停运或空载情况下进行，主要有短路试验、抛载试验［3-4］和静态频域响应法［5-7］等。极端试验对发电机的冲击较大，且存在一定的危险性。尽管已有IEEE标准规定了利用静态频域响应法获取同步电机参数的步骤［8］，但该方法比较耗时，且难以准确代表正常运行状态下同步发电机的特征［9］。而在线辨识考虑了运行工况，更符合实际情况［10］。在线辨识时，常用的辨识方法有时域辨识法［11-13］和频域辨识法［14-15］。 但利用时域辨识法进行同步发电机参数辨识存在一定的困难，仍有很多工作要做［16］。 文献［14］利用在线频域法进行辨识，但求得的同步发电机基本参数具有多值性，不可唯一辨识，其原因在于所辨识的中间变量个数少于基本参数。文献［15］中模型的直轴和交轴（dq轴）阻抗矩阵为二阶矩阵，矩阵元素个数少于同步发电机基本参数，基本参数也无法唯一辨识。

针对现有频域辨识法不能唯一辨识基本参数的问题，本文在文献［15］方法的基础上，考虑励磁电压和励磁电流等可观测量，增加中间变量，建立由dq轴电流电压、励磁电压和励磁电流等可观测量表示的同步发电机阻抗矩阵传递函数模型，以解决同步发电机基本参数唯一性求取的问题。由于单一频率下的信号无法唯一辨识同步发电机基本参数，本文利用一对信号的频域信息，来达到唯一辨识基本参数的目的。结合粒子群优化算法辨识阻抗矩阵各元素值，再由阻抗实部和虚部分开表征的辨识算法，来辨识同步发电机基本参数。利用本文方法，同步发电机模型基本参数是唯一可辨识的，可避免参数多值性问题，且辨识过程与参数经验值无关，能有效防止出现由参数经验值误差引起辨识精度降低的问题。通过算例仿真验证了本文辨识模型和算法的正确性。

1 同步发电机阻抗矩阵传递函数模型

为了唯一辨识同步发电机基本参数，本文以派克模型为基础建立由dq轴电流电压、励磁电压和励磁电流等可观测量表示的同步发电机模型。同步发电机的派克模型中，电压方程为：

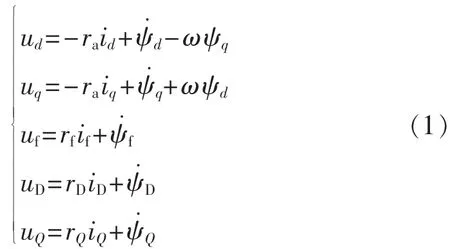
其中，uD=uQ=0。磁链方程为：

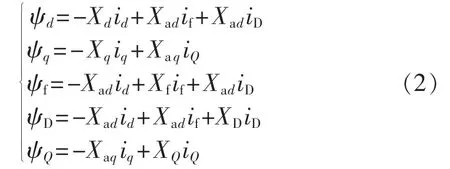
各变量含义参见文献［1］。

对式（1）中的第4式进行拉氏变换，并将式（2）代入得：

对式（1）中的第5式进行拉氏变换，并将式（2）代入得：

对式（1）中的第1—3式进行拉氏变换，并将式（2）—（4）代入，可得电压和电流之间的传递函数关系式：

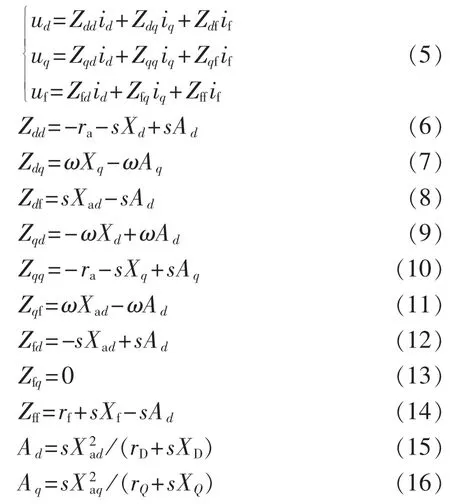
在扰动情况下，由式（5）可将同步发电机基本参数辨识模型写为由可观测量表示的阻抗矩阵传递函数模型：

其中，Δ表示稳态运行点上的小扰动。

式（17）模型中阻抗矩阵为三阶，直轴、交轴和励磁（dqf）阻抗矩阵中的元素均可作为中间变量，明显比文献［15］中模型的中间变量要多，大幅降低了同步发电机基本参数唯一辨识的难度。

2 可辨识性分析

下面分析同步发电机阻抗矩阵传递函数模型与基本参数之间的关系。为了更好地观察dqf阻抗矩阵的特点，有利于进一步辨识，将式（17）所示模型的实部、虚部分开，并假设发电机转速不变，即ω=1，则模型也可写成如下形式：

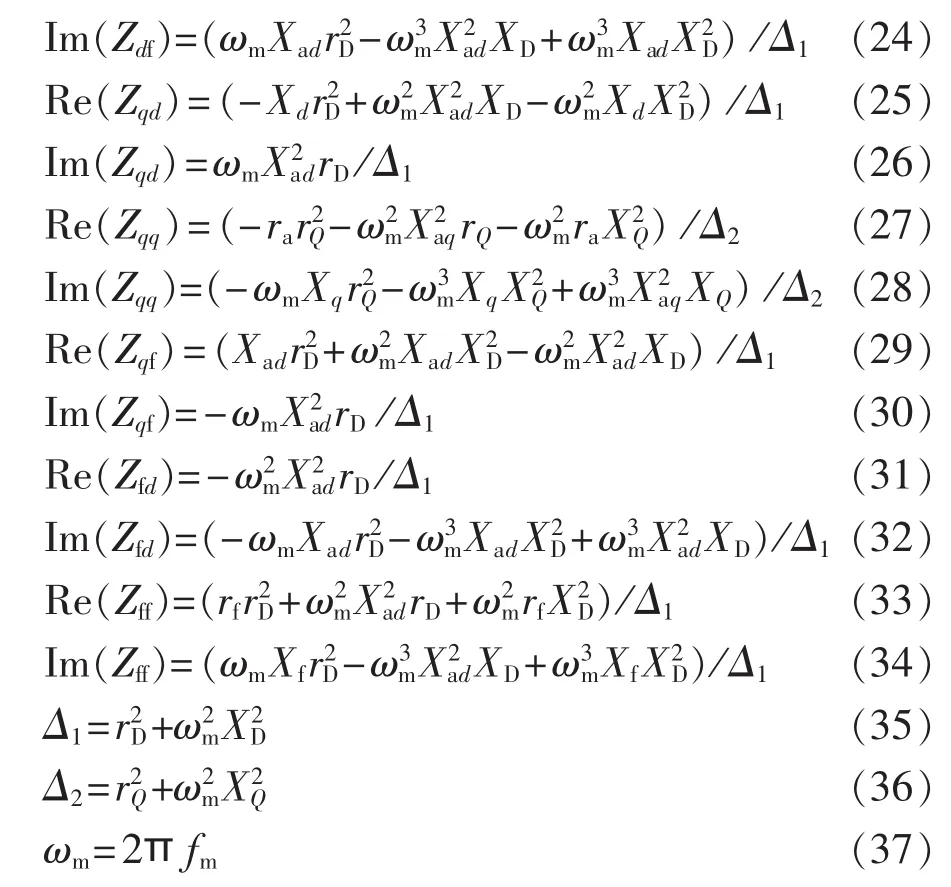
fm的具体含义将在后文述及。A是满足式（18）的矩阵，由于篇幅限制，此处不再列写。

可以看出，dqf阻抗矩阵中存在如下线性相关关系：

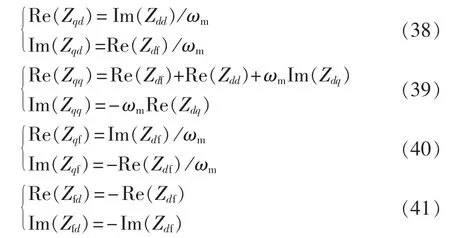
因此，式（18）可表示为含 Re（Zdd）、Re（Zdq）、Re（Zdf）、Re（Zff）、Im（Zdd）、Im（Zdq）、Im（Zdf）和Im（Zff）8 个未知数、6个方程的欠定方程组。而当fm取一对相反数时，dqf阻抗矩阵中各阻抗的实部不变，虚部互为相反数。因此，可列写出含8个未知数、12个方程的超定方程组，求解方程组即可获得dqf阻抗矩阵中各元素的值。

由式（19）和式（23）可得：

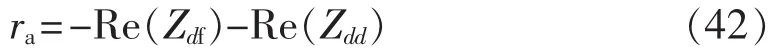
由式（23）和式（33）可得：

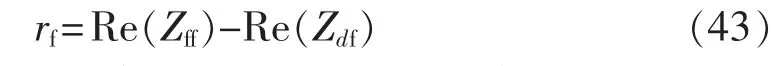
由式（20）和式（24）可得发电机漏抗：

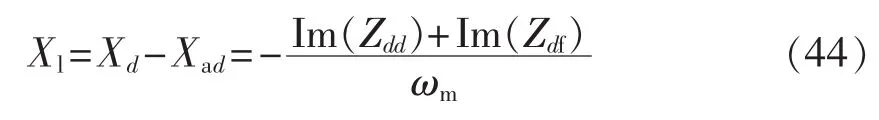
因此，ra、rf、Xl唯一可辨识。

利用稳态电压方程式（45）可求得Xq。

由此还可得到：

再利用稳态电压方程式（47）并结合式（44）联立方程组解得 Xd、Xad。

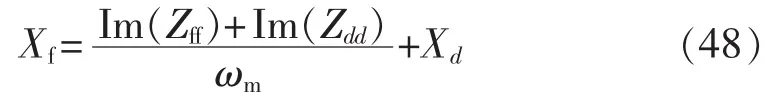
由式（20）和式（23）可求得 rD和XD，由式（21）和式（22）可求得 rQ和XQ。

同理可对文献［15］中的频域模型进行可辨识性分析，该模型的dq阻抗矩阵中元素的实部虚部是线性独立的，由于篇幅限制，表达式略。因此，文献［15］模型可表示为含 Re（Zdd）、Re（Zdq）、Re（Zqd）、Re（Zqq）、Im（Zdd）、Im（Zdq）、Im（Zqd）和Im（Zqq） 8 个未知数、4 个方程的欠定方程组。当fm取2个不同的数时，可列写出含8个未知数、8个方程的方程组，求解方程组即可获得dq阻抗矩阵中各元素的值。该模型中阻抗矩阵为二阶，利用阻抗实部和虚部分开表征的辨识算法，只有8个中间变量，但需要求解的基本参数有10个，如果没有其他已知条件，基本参数存在多值解，不可唯一辨识。即使假设其中2个基本参数已知，中间变量与基本参数的关系式十分复杂，可辨识性问题也要视具体情况而定。

上述分析表明，利用阻抗实部和虚部分开表征的辨识算法，结合稳态电压方程，本文所提模型的所有基本参数均是唯一可辨识的，而文献［15］模型的基本参数不可唯一辨识。

因此，利用稳态方程，Xd、Xad、Xq、Xaq唯一可辨识。

再由式（20）和式（34）可得：

3 同步发电机基本参数辨识方法

3.1 频域输入信息

由于单一频率下的信号无法唯一辨识同步发电机基本参数，需增加频率信号。因此，可利用静止同步串联补偿器（SSSC）注入小信号电压，实现原理如图1所示。通过采集机端三相电压信号，控制输出电压，经3个单相双绕组变压器耦合小信号注入。注入小信号不会影响系统正常运行状况，转速可基本保持恒定［15，17］。

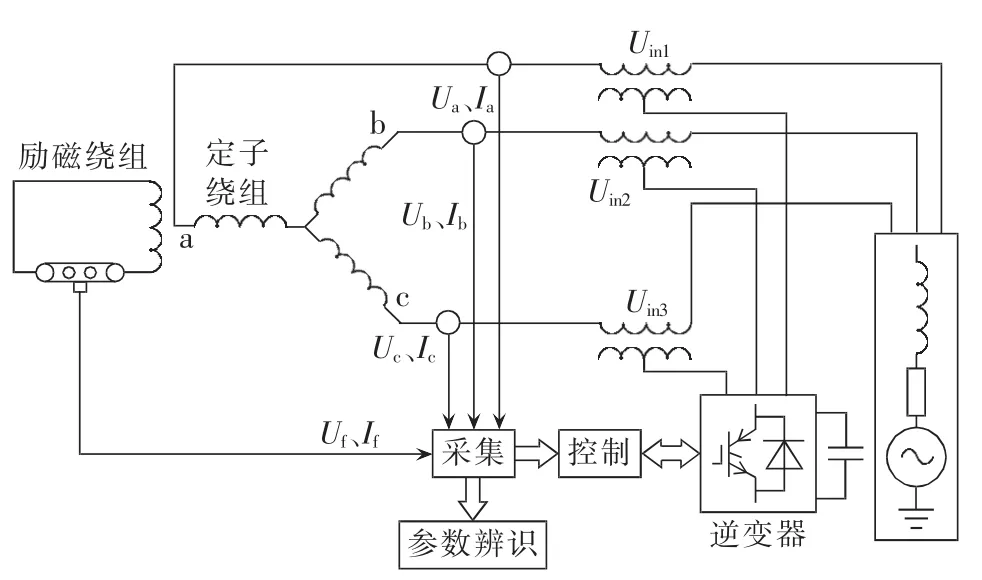
图1 利用SSSC产生小信号电压原理图Fig.1 Schematic diagram of small signal voltage generation with SSSC

设小信号电压如下：

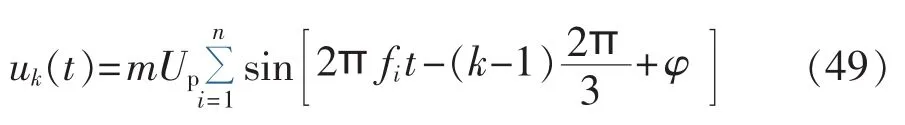
其中，k=1，2，3 分别表示 a、b、c 三相；m 为调幅深度，取0.05%；Up为工频电压峰值；fi为注入间谐波频率；φ为初始相角。

频率为fi的间谐波电压信号经dq变换后得：

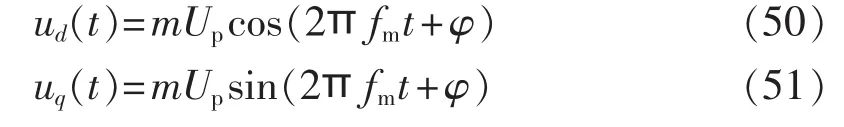
其中，fm=fi-fe，fe=50 Hz。

由式（50）和式（51）可以得出，在dq坐标系中，注入的间谐波电压仅包含频率为fm的分量。

注入一对频率关于基频对称的小信号，利用自适应滤波［18-19］得到信号的频域信息。由于间谐波频率下，辨识出的发电机电抗参数都乘以了系数fe／fi，因此，对间谐波频率下辨识出的电抗参数须除以系数fe／fi，以转换为工频情况下的电抗参数。

3.2 粒子群优化算法

由第2节的分析可知，求解超定方程组得到dqf阻抗矩阵中各元素的值后，就能唯一辨识同步发电机的各个基本参数。因此，矩阵中各元素值的精确性会影响辨识结果的精确性。

粒子群优化算法是一种群体智能算法，该算法模拟社会的群体行为，在空间中进行全局寻优，操作简便，依赖的经验参数较少，收敛速度较快［20-21］。为了提高辨识精度，本文结合粒子群优化算法寻找dqf阻抗矩阵中各元素的最优解，采用的目标函数为：

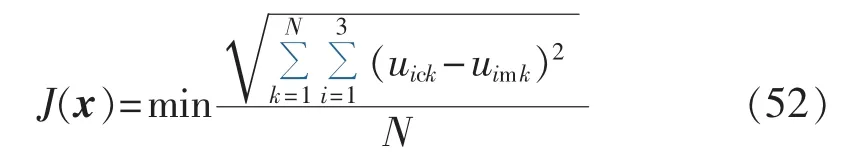
其中，N为注入频率的个数；u1ck、u2ck和u3ck分别为d轴电压、q轴电压和励磁电压的计算值；u1mk、u2mk和u3mk分别为d轴电压、q轴电压和励磁电压的测量值。算法的具体操作步骤见文献［21］。

4 算例仿真

仿真系统为单机无穷大系统［22］。系统基本参数为：发电机容量S=500 kV·A，额定电压U=10.5 kV，ra=0.003，rf=0.0006358，rD=0.004654，rQ=0.006183，Xd=1.116，Xq=0.416，Xf=1.083，XD=0.966 833，XQ=0.232174，Xad=0.91763，Xaq=0.21763。其中，所有阻抗参数均为标幺值。输入机械功率与励磁电压保持恒定不变。

用MATLAB／Simulink进行仿真计算。观测量干扰采用服从正态分布N（0，0.005）的噪声信号。

为提高辨识精度，本文分别向系统注入25 Hz、30 Hz、35 Hz、40 Hz、45 Hz、55 Hz、60 Hz、65 Hz、70 Hz、75 Hz这10组频率，获得各频率小信号电压暂态过程和稳态过程发电机出口dq轴电压电流、励磁电压、励磁电流等数据。关于50 Hz对称的频率两两为一对，进行辨识运算。以注入40 Hz和60 Hz间谐波为例，未加噪声前各观测量的波形如图2所示，图中纵轴均为标幺值。

利用自适应滤波得到信号的频点信息，以注入40 Hz和60 Hz间谐波为例，滤除噪声信号和直流分量后，各观测量的频谱如图3所示。

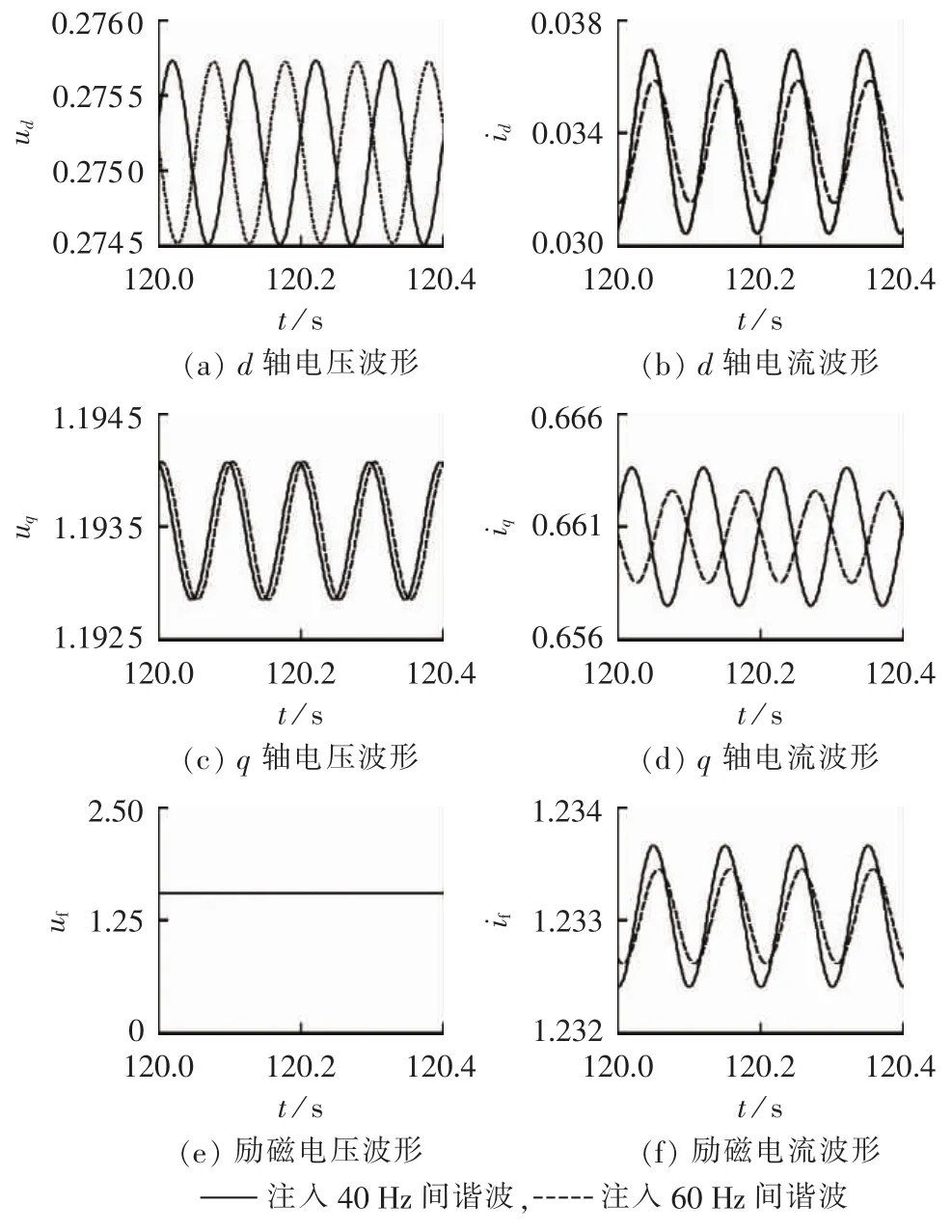
图2 注入40 Hz和60 Hz间谐波时各观测量波形Fig.2 Waveforms of measurable variable，when 40 Hz and 60 Hz signals are injected

图3 注入40 Hz和60 Hz间谐波时各观测量频谱图Fig.3 Spectrums of measurable variable，when 40 Hz and 60 Hz signals are injected

结合粒子群优化算法寻找dqf阻抗矩阵中各元素的最优解，粒子群优化算法的参数搜索上限为矩阵元素真值的2倍，下限为50%。辨识得到矩阵元素的值后，再根据第2节中的步骤辨识同步发电机基本参数。将辨识得到的5组同步发电机基本参数取平均值。文献［15］模型的基本参数不可唯一辨识，因此假设Xad和rf已知，Xad和rf取真值进行辨识，再取5%误差时进行辨识，同步发电机基本参数辨识结果如表1所示，表中真值、辨识值为标幺值。

由表中结果可见，文献［15］方法的辨识精度与基本参数的经验值密切相关：当所选基本参数取真值时，文献［15］的辨识方法精度较高，而当参数根据经验值取5%误差进行辨识时，精度就比较差。而本文方法与基本参数的经验值无关，辨识结果精度高。

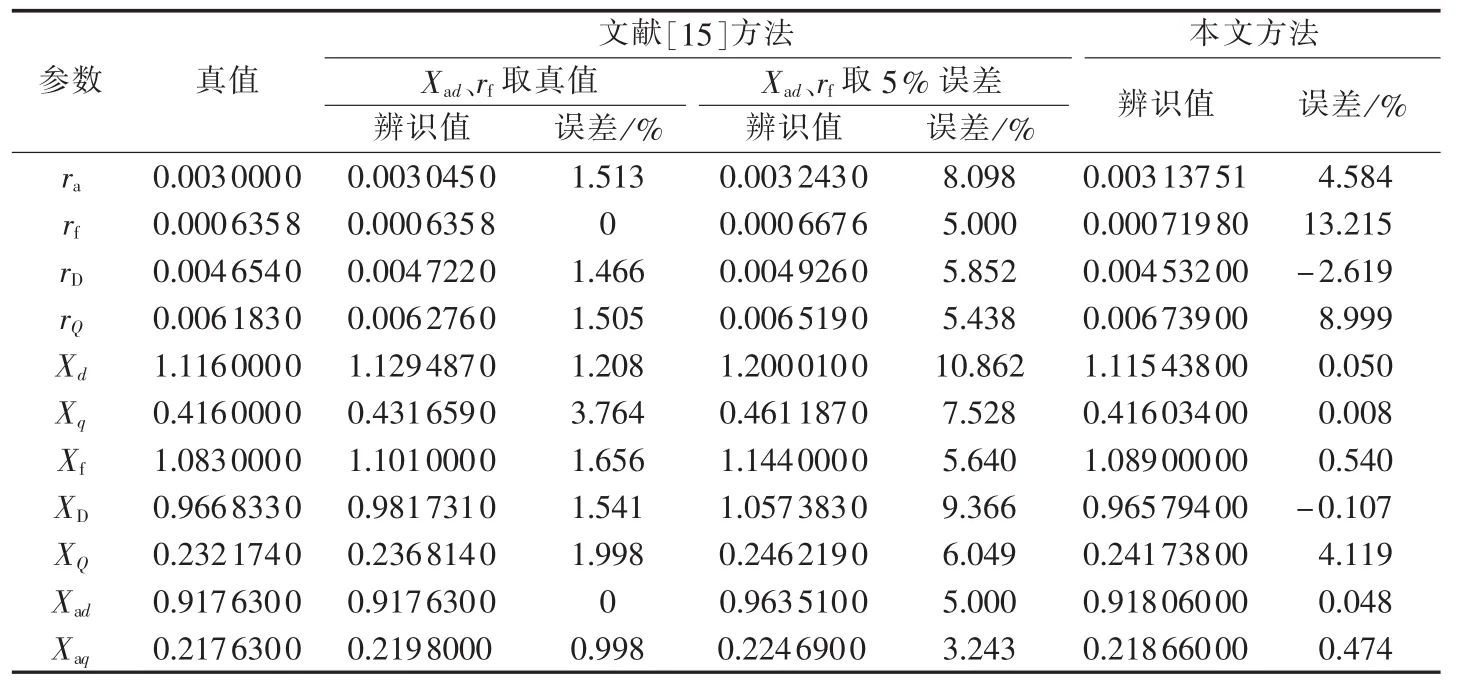
表1 同步发电机基本参数辨识结果Table 1 Results of basic parameter identification for synchronous generator

利用文献［15］方法，将Xad和rf取不同的误差进行辨识，该方法辨识得到的同步发电机参数最大相对误差绝对值与所选基本参数的经验值误差关系如图4所示。

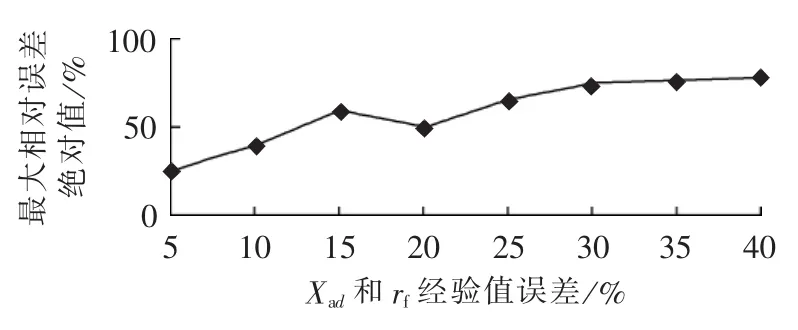
图4 文献［15］方法参数辨识值最大相对误差绝对值与所选基本参数的经验值误差关系Fig.4 Relationship between absolute maximum relative error of parameters identified by reference［15］and empirical value error of selected basic parameters

由图4可以看出，随着Xad和rf经验值误差的增加，文献［15］方法辨识得到的同步发电机参数的最大相对误差绝对值呈增加的趋势。而本文方法与基本参数的经验值无关，直接对各个基本参数进行辨识。利用本文方法与文献［15］方法Xad和rf取20%误差，多次辨识得到的同步发电机参数最大相对误差绝对值如图5所示。

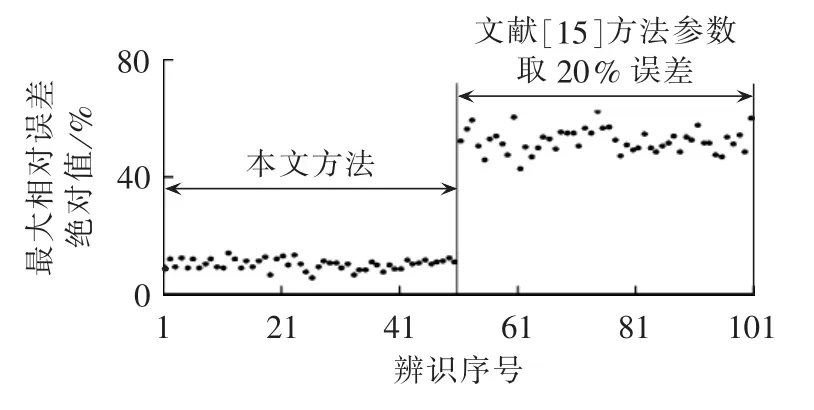
图5 参数辨识值最大相对误差绝对值Fig.5 Absolute maximum relative error of identified parameters

由图5可以看出，文献［15］方法受所选基本参数的经验值误差影响较大，精度较差，而利用本文方法每次辨识得到的同步发电机参数的最大相对误差变化不大，能有效地防止出现由参数经验值误差引起辨识精度降低的问题，辨识结果精度较高，因此，本文所提出的辨识模型和方法有效、可行。

5 结论

本文建立了由可观测量表示的同步发电机阻抗矩阵传递函数辨识模型，并对模型的基本参数进行辨识。

a.该模型的所有变量都是可观测的，保证了辨识所得参数的准确性和平稳性，并有效地简化了辨识过程。

b.阻抗实部和虚部分开表征的辨识算法有利于观察dqf阻抗矩阵的特点，并从理论上分析了本文所提出的模型参数是唯一可辨识的。

c.利用一对信号频域信息进行辨识，结合粒子群优化算法，收敛速度快，辨识精度高。

仿真结果表明：文献［15］方法辨识精度与基本参数的经验值密切相关；本文的模型是唯一可辨识的，避免了参数多值性问题，辨识过程与参数经验值无关，能有效防止出现由参数经验值误差引起辨识精度降低的问题，辨识所得的结果精度较高，表明本文所提出的辨识模型和方法的合理性和有效性。

［1］倪以信，陈寿孙，等.动态电力系统的理论和分析［M］.北京：清华大学出版社，2002：1-59.

［2］鞠平.电力系统非线性辨识［M］.江苏：河海大学出版社，1999：48-66.

［3］岳陈熙，甄威，刘柏私，等.同步发电机参数的一次性任意抛载测试方法［J］.高电压技术，2008，34（2）：319-323.YUE Chenxi，ZHEN Wei，LIU Bosi，et al.New load rejection test method for parameter estimation of synchronous generators ［J］.High Voltage Engineeering，2008，34（2）：319-323.

［4］寇攀高，周建中，肖剑，等.基于多新息最小二乘法的同步发电机一次性抛载试验参数辨识［J］.电网技术，2013，37（2）：378-384.KOU Pangao，ZHOU Jianzhong，XIAO Jian，et al.Multi-innovation leastsquarealgorithm-based parameteridentification forsynchronous generator by once-only load rejection test［J］.Power System Technology，2013，37（2）：378-384.

［5］ESCARELA-PEREZ R，NIEWIEROWICZ T.Synchronous machine parameters from frequency-response finite-element simulations and genetic algorithms［J］.IEEE Transactions on Energy Conversion，2001，16（2）：198-203.

［6］BORTONI E C，JARDINI J A.A standstill frequency response method for large salient pole synchronous machines［J］.IEEE Transactions on Energy Conversion，2004，4（19）：687-691.

［7］GHASSEMI M，LESANI H.Synchronous machine modelling and identification via network equivalent techniques［C］∥Proceedings of Large Engineering Systems Conference on Power Engineering.Montreal，Quebec，Canada：IEEE，2007：24-29.

［8］IEEE.IEEE standard proceduresforobtaining synchronous machineparametersbystandstillfrequency responsetesting：IEEE Std 115A-1987［S］.［S.l.］：IEEE，1987.

［9］VYNCKE T J，DE BELIE F M.Identification of PM synchronous machines in the frequency domain by broadband excitation［C］∥Proceedings of International Symposium on Power Electronics，Electrical Drives，Automation and Motion.Ischia，Italia：IEEE，2008：1253-1258.

［10］伍双喜，张伯明，吴文传，等.基于实测系统扰动的同步发电机参数辨识与验证［J］.电网技术，2012，36（11）：87-93.WU Shuangxi，ZHANG Boming，WU Wenchuan，et al.Identification and validation for synchronous generator parameters based on recorded on-line disturbance data［J］.Power System Technology，2012，36（11）：87-93 .

［11］孙黎霞，鞠平.基于Park模型的同步发电机参数辨识［J］.中国电机工程学报，2009，29（19）：50-56.SUN Lixia，JU Ping.Parameter estimation of synchronous generator based on Park model［J］.Proceedings of the CSEE，2009，29（19）：50-56.

［12］罗建，冯树辉，蔡明，等.基于可观测量的同步发电机参数的时域辨识［J］.电力系统自动化，2011，35（7）：24-28.LUO Jian，FENG Shuhui，CAI Ming，et al.Time domain parameter identification of synchronous generator based on measurable variables［J］.Automation of Electric Power Systems，2011，35（7）：24-28.

［13］BORTONI E C，JARDINI J A.Identification of synchronous machine parameters using load rejection test data［J］.IEEE Transactions on Energy Conversion，2002，17（2）：242-247.

［14］金宇清，岳陈熙，甄威，等.基于功角测量的同步发电机参数辨识频域法［J］.电力系统自动化，2007，31（4）：7-11.JIN Yuqing，YUE Chenxi，ZHEN Wei，et al.On-line frequency response method of synchronous machine parameter identification based on rotor angle measurement［J］.Automation of Electric Power Systems，2007，31（4）：7-11.

［15］HUANG J，CORZINE K A.Online synchronous machine parameter extraction from small-signal injection techniques［J］.IEEE Transactions on Energy Conversion，2009，24（1）：43-51.

［16］鞠平，倪腊琴.同步发电机参数辨识的模拟进化方法［J］.电工技术学报，1999，14（5）：1-4.JU Ping，NI Laqin.Simulated evolutionary approaches to parameter estimation of synchronous machine［J］.Transactions of China Electrotechnical Society，1999，14（5）：1-4.

［17］FAMILIANT Y L，CORZINE K A.AC impedance measurement techniques［C］∥Proceedings of IEEE International Conference on Electric Machines and Drives.San Antonio，Texas，USA：IEEE，2005：1850-1857.

［18］雷云飞，杨高才.用于变压器局部放电在线监测的改进NLMS自适应滤波算法［J］.电网技术，2010，34（8）：165-169.LEI Yunfei，YANG Gaocai.An improved adaptive normalized least mean square filtering algorithm for on-line monitoring of transformer partial discharge［J］.Power System Technology，2010，34（8）：165-169.

［19］尹刚，司瑞琦.自适应滤波器在提高持续正弦信号采样精度中的应用［J］.重庆大学学报（自然科学版），2012，35（3）：98-102.YIN Gang，SI Ruiqi.The application research on improvement ofconstantsinusoidalsignalsampling precision based on adaptive filter［J］.Journal of Chongqing University（Natural Science Edition），2012，35（3）：98-102.

［20］袁晓辉，王乘，张勇传，等.粒子群优化算法在电力系统中的应用［J］.电网技术，2004，28（19）：14-19.YUAN Xiaohui，WANG Cheng，ZHANG Yongchuan，etal.A survey on application of particle swarm optimization to electric power systems［J］.Power System Technology，2004，28（19）：14-19.

［21］何怡刚，祝文姬.基于粒子群算法的模拟电路故障诊断方法［J］.电工技术学报，2010，25（6）：163-171.HE Yigang，ZHU Wenji.An analog circuit diagnosis method based on particle swarm optimization algorithm［J］.Transactions of China Electrotechnical Society，2010，25（6）：163-171.

［22］王晶.电力系统的 MATLAB／Simulink仿真与应用［M］.西安：西安电子科技大学出版社，2008：92-136.