基于环流提取法的近似零电流换相低谐波双反星形整流器
王景芳,杨世彦,杨 威
(哈尔滨工业大学 电气工程及自动化学院,黑龙江 哈尔滨 150001)
0 引言
二极管整流电路具有结构简单、运行可靠、价格低廉等优点,被广泛用作各种电力电子装置与电网的接口电路,然而二极管整流电路的强非线性会使得大量谐波电流注入电网,产生严重的谐波污染,给用电设备带来一系列危害。整流电路中的变压器漏感和线路的杂散电感使得二极管换相不能瞬间完成,产生换相重叠,引起输出电压换相压降,降低了整流器的输出能力和系统效率。
目前解决整流器谐波污染问题的主要方法有2种:装设各种有源、无源以及混合型电力滤波器,但这会使系统成本和能量损耗有所增加[1-3];改进整流技术,使其不产生或尽量少产生谐波。后者又可分为PWM整流技术[4-6]和多脉波整流技术。多脉波整流器具有低复杂度、高可靠性、高变换效率和强过载能力等优点,被广泛应用于大功率场合[7-9]。但常规多脉波整流技术只能抑制有限次数的低次谐波,而对高次谐波无能为力。为了克服常规多脉波整流器的缺点,近些年来,国内外学者提出了各种基于直流侧谐波抑制技术的多脉波整流系统,大多数方案都能在对原整流系统的体积和容量不造成大的增加的前提下主动地显著抑制输入电流谐波[9-16]。然而,这些方案在分析时,均未考虑变压器的漏感对系统产生的影响,也未给出直流侧的电流调制对换相过程的影响。
在低压大电流场合,双反星形整流电路较其他结构的整流电路能够获得更高的效率,因此被广泛应用,然而其输入电流谐波含量很高,换相过程对系统的影响也更为严重[17-19]。为了有效减少双反星形整流器的输入电流谐波并显著改善整流器的换相过程,考虑变压器漏感对整流器的影响,提出了一种新的直流侧环流提取方法,并深入分析了提取的直流侧环流对换相过程的改善作用,得到了一种近似零电流换相的低谐波整流器。
1 考虑漏感所需提取的环流
直流侧带环流提取电路的双反星形整流器如图1所示。
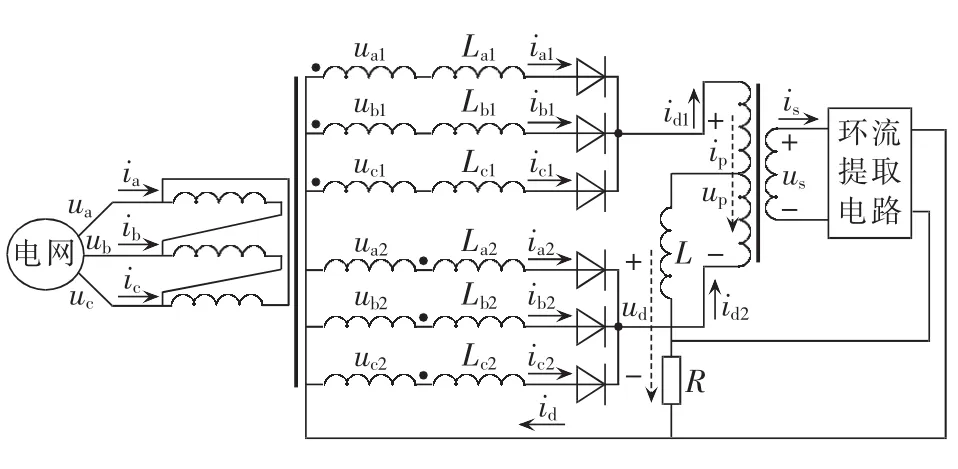
图1 带环流提取电路的双反星形整流器Fig.1 Double-star rectifier with circuiting current extraction circuit
变压器的漏感用折算到变压器二次侧的集中电感 La1、Lb1、Lc1和La2、Lb2、Lc2来表示。
在进行理论分析之前,做以下假设:
a.双反星形整流器的输出为大电感负载,且输出电感足够大,输出电流纹波为零;
b.双反星形整流器的输入电压为三相对称的标准正弦波电压;
c.二极管为理想器件,磁性器件与线路电阻为零;
d.变压器的各相漏感相同,如式(1)所示。

1.1 考虑漏感时所需提取的环流分析
如图1所示,根据安匝平衡原理和基尔霍夫电流定律,双反星形变压器输入电流和输出电流的关系为:
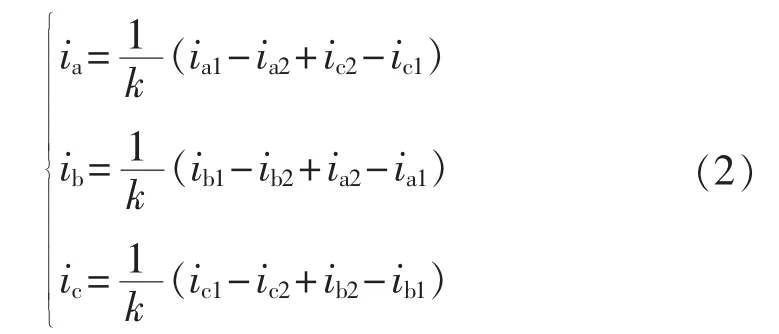
其中,k为双反星形变压器的原、副边绕组匝比。
设平衡电抗器原、副边绕组的匝比为Np∶Ns=1∶m,环流ip的参考方向如图1所示,由整流器结构的对称性,两三相半波整流桥的输出电流id1和id2满足下式:
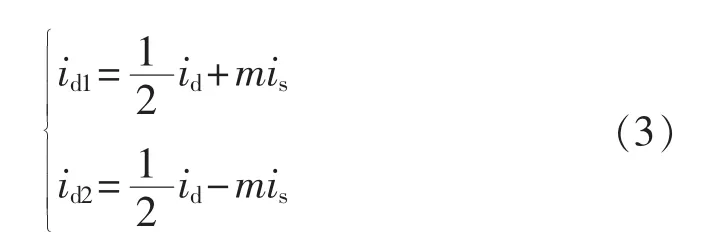
其中,is为环流生成电路从平衡电抗器副边提取的环流。
两三相半波整流桥的输入电流和输出电流关系分别为:
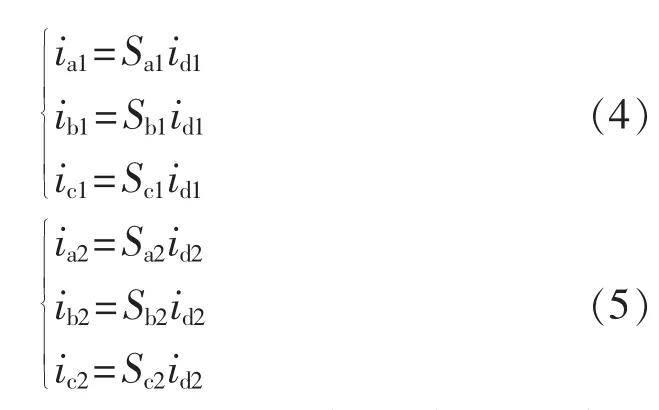
其中,Sa1、Sb1、Sc1、Sa2、Sb2、Sc2为整 流桥的 实 际开 关 函数,它描述了考虑变压器漏感时三相半波整流桥的输入电流和输出电流之间的关系,这与之前的其他直流侧谐波抑制方案采用理想开关函数进行分析不同。
这些实际开关函数之间满足如下相位关系:

大电感条件下,整流器的输出电流可以认为是恒定值 Id,将式(3)—(5)代入(2)得输入电流 ia、ib和ic,整流器的输出电流Id和提取的环流is之间的关系为:


由上面的分析可知,通过控制提取环流的大小,可以改变两三相半波整流桥的输出电流,从而改变换相过程和系统的输入电流。为了获得使整流器输入电流谐波得到有效抑制的环流,设输入电流为正弦波,输出电压的平均值等于理想直流输出电压Ud0时,输出电压的换相压降被消除,此时输入电流 ia、ib、ic,整流器的输出电流Id和环流is之间满足如下关系:
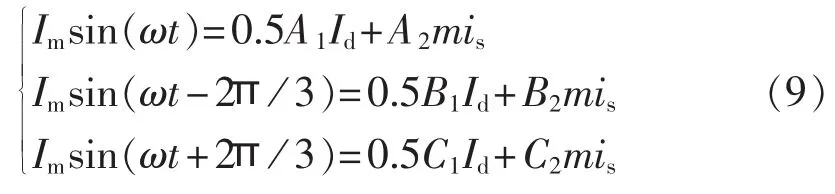
其中,Im为整流器的输入电流;整流器的输出电流Id满足式(10)。

其中,Um为整流器输入电压幅值;R为负载电阻;Ud0为变压器漏感为零时,整流器的平均输出直流电压。
解式(9)得:
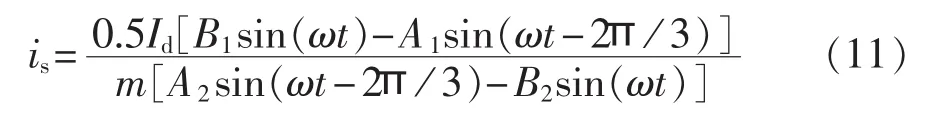
所需提取环流is的波形如图2所示。

图2 环流is的波形Fig.2 Waveform of circulating current is
由图2和式(10)可知,考虑变压器漏感的影响后,得出的所需提取的环流is为一个周期内具有6个间断点的频率等于150 Hz的不规则周期波,在每个区间为提取环流后的换相重叠角)有以下缺点:
a.存在一个无穷型间断点,波形不规则且幅值变化剧烈,实际实现困难;
b.在这个区间的大部分区域内,环流幅值绝对值大于0.5Id/m,这意味着在直流侧提取的环流将使得三相半波整流桥的输出电流为负,然而由于二极管的单相导电性,整流桥的输出电流不能为负。
1.2 环流提取电路的实现
为了便于实际电路的实现,考虑到所需提取的环流is存在的上述问题,将区间内的电流波形用斜线段代替(如图2中的虚线所示),此时注入电流波形非常接近三角波,可采用频率等于150 Hz、幅值等于0.5Id/m且与环流is同相位的三角波环流代替所需提取的环流is,三角波环流在一个工频周期内的表达式为:

为了将上述的三角波环流从整流器的直流侧提取出来,环流提取电路采用单相全控桥结构。图3为环流提取电路的原理框图,其输入与平衡电抗器的副边连接,与平衡电抗器形成有源平衡电抗器AIPR(Active Inter-Phase Reactor),其输出与双反星形整流器的负载并联,以实现谐波能量回馈。注入电流的给定信号由同步单位三角波信号与直流输出电流的平均值信号相乘得到,当系统的输入电压或负载发生变化时,环流给定信号也相应变化,使系统在较宽的范围内具有良好的调制效果。
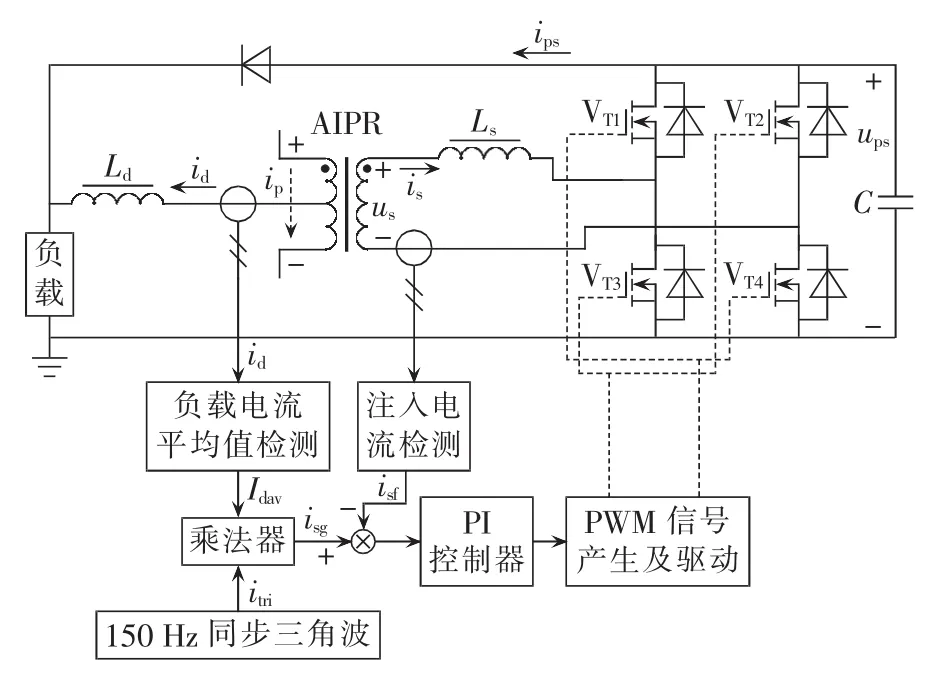
图3 环流提取电路及其控制系统框图Fig.3 Circulating current extraction circuit and its control system
2 环流对换相和谐波的作用机理
2.1 二次换相的产生机理分析
当在平衡电抗器的副边提取三角波环流i*s后,整流器直流侧的电压和电流波形被相应地改变,如图4所示。图中,U2为双反星形变压器副边电压的有效值。
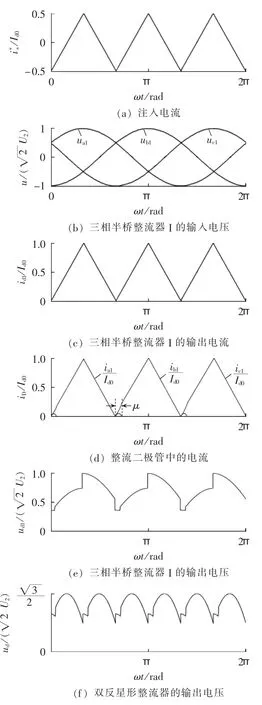
图4 注入电流后整流器直流侧的波形Fig.4 DC-side waveforms of rectifier with current injection
如图4所示,在双反星形整流器的直流侧提取三角波环流后,由于叠加了环流在漏感上产生的压降,三相半桥整流器的输出电压发生了改变,但由于双反星形整流器结构的对称性,非换相期间,环流在两三相半桥整流器输出电压上叠加的漏感压降被相互抵消。
在平衡电抗器的副边提取三角波环流后,三相半桥整流器Ⅰ的输出电流id1被调制为临界导通的直流三角波电流,此时id1的表达式为:

由图4和上式可知,在换相时刻,提取的三角波环流将三相半波整流器的输出电流id1恰好调制为零,改变了换相时刻半波整流器的输出电流状态,使整流器的换相模式发生改变,整流器按照新的模式进行换相。
下面以a1相和b1相二极管换相为例,介绍这种新的换相模式。
如图1和图4所示,在a1相和b1相换相开始之前,三相半桥整流器的输出电流id1通过a1相二极管向负载供电,在换相时刻a1相二极管中的电流恰好下降为零,输出电流id1在零电流的条件下由a1相二极管换流到b1相二极管,a1相二极管自动关断,b1相二极管自动导通,然而当输出电流id1流过b1相二极管时,其在b1相漏感上产生的压降使a1相二极管再次承受正向电压,a1相二极管和b1相二极管再次同时导通,产生新的换相过程,直到流过b1相二极管中的电流增加到与三相半桥整流器的输出电流id1相同时,新的换相过程结束。
新的换相过程产生的原因与传统整流理论中换相过程产生的原因完全不同。它是在换相时刻零电流换相后立刻产生的又一次新的换相,可以称其为“二次换相”。
2.2 二次换相的换相重叠角和换相压降
由上面的分析可知,注入电流后双反星形整流器每个工频周期发生6次二次换相,由于二次换相的产生机理是一致的,对其中的一个二次换相过程进行分析即可。下面以a1相和b1相二极管换相为例,分析二次换相的换相重叠角和换相压降与电路参数之间的关系表达式。
在a1相二极管和b1相二极管二次换相期间可得如下等式:

结合式(13),可解得:
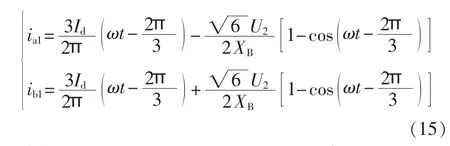

由式(16)可知,二次换相产生的换相重叠角与变压器的漏感和负载电流成正比,与变压器的副边电压成反比。
大多数情况下,传统整流器的换相重叠角μ*在10°以内。据式(16)和传统的整流理论,在相同的电路参数条件下,图5给出了此范围内环流提取前后,整流器换相重叠角之间的关系曲线。
其中,XB=ωL为双反星形变压器的漏感抗。
当b1相二极管中的电流增加到与三相半桥整流器的输出电流id1相同,即ib1=id1时,二次换相过程结束,设此时 ωt=2π/3+μ,由式(15)得,二次换相产生的换相重叠角μ满足:

图5 提取环流前后换相重叠角之间的关系Fig.5 Comparison of overlap angle between with and without circuiting current extraction
由图5可知,电路参数相同时,直流侧提取三角波环流后,产生的二次换相重叠角明显小于原整流器的换相重叠角,且原系统的换相重叠角越小,注入电流后产生的二次换相重叠角则越小。传统整流器的换相重叠角μ*在10°以内时,注入电流后,换相重叠角被减小到1.7°以内,换相重叠角几乎被消除。
在a1相二极管和b1相二极管二次换相期间,两三相半桥整流器的输出电压分别为:
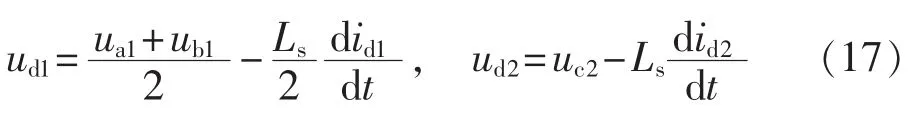
整流器输出电压的瞬时值为:

整流器的换相压降为:

其中,ud0为变压器漏感为零时,整流器的输出电压。
由上式可知,二次换相产生的换相压降恒为零,提取的三角波环流能够完全消除由变压器漏感所引起的换相压降。
由上面的分析结果可知,从平衡电抗器副边提取三角波环流后,整流器的换相过程被显著改善,尽管换相重叠角没有被完全消除,但变压器漏感引起的输出电压换相压降被完全消除,这与传统的整流器理论完全不同。
2.3 二次换相对谐波抑制作用的影响
如图3所示,从直流侧提取三角波环流后,双反星形变压器副边电流被调制为近似三角波的工频脉冲电流,与标准的三角波工频脉冲电流相比其增加了二次换相部分。为了明确二次换相部分对谐波抑制作用的影响,下面对二次换相过程中的电流进行分析。
在a1相二极管和b1相二极管二次换相期间,即对式(15)中的 a1相电流 ia1求导可以得到ia1在处取得最大值 imax,a1:

由式(20)可得:

由图4可知,传统整流器的换相重叠角在10°以内时,提取三角波环流后,整流器的换相重叠角被减小到 1.7°以内,由式(21)可得,此时:

二次换相重叠角和其引起的电流变化都很小,注入电流后,双反星形整流器几乎工作于零电流换相状态,二次换相对变压器副边电流的影响可以忽略,可认为提取环流后,变压器副边的电流被调制为标准的工频三角波脉冲电流,可将标准的工频三角波脉冲电流代入式(2),分析三角波注入电流对输入电流的谐波作用抑制作用。
结合双反星形变压器副边输出电流的相位关系,将被提取的环流调制为三角波脉冲的变压器副边输出电流代入式(2),并用傅里叶级数展开得:
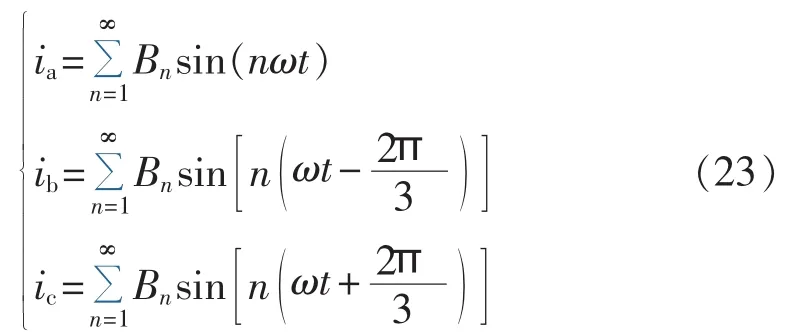
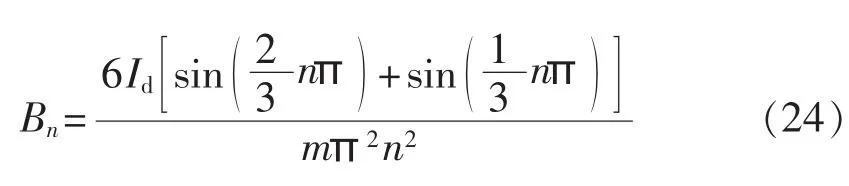
由式(24)可知,提取环流后,输入电流的6k±1次谐波得到显著抑制,系统的输入电流近似为正弦波,输入电流的THD减小为4.6%。
3 实验结果
为了验证理论分析结果的正确性,研制了一台功率为1.1 kW实验样机,实验样机主要参数如下:输入线电压有效值为380 V,变压器原副边变比为29∶6,负载滤波电感为15 mH,平衡电抗器变比为1∶1,环流提取电路开关频率为40 kHz,环流提取电路输入电感为1.8 mH。
图6—8为由15 mH的滤波电感和7.5 Ω的电阻共同组成大电感负载时的实验波形。
图6分别为原双反星形整流器和直流侧带环流提取电路的双反星形整流器的直流侧主要波形。如图6(a)所示,原双反星形整流器的换相重叠角为9°,输出电压存在换相压降,平均直流输出电压90.4 V;如图6(b)所示,直流侧带环流提取电路的双反星形整流器的换相重叠角基本被消除,与理论分析值(换相重叠角减到1.4°)基本一致,整流器近似零电流换相,输出电压换相压降被消除,平均直流输出电压提高为90.7 V。
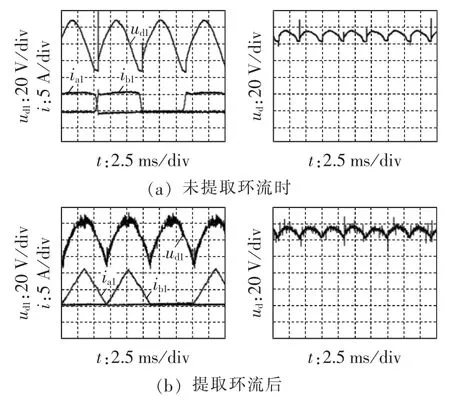
图6 环流提取前后整流器直流侧的主要波形Fig.6 DC-side waveforms of rectifier with or without circuiting current extraction
图7(a)为原双反星形整流器的输入电流和电压波形,输入电流波形近似为阶梯波,利用日置三相电能分析仪3196测得此时输入电流的THD=25.9%,功率因数PF=0.95;图7(b)为提出的双反星形整流器的输入电流和电压波形,输入电流波形近似为正弦波,输入电流的THD下降为4.73%(与理论分析值基本一致),功率因数提高为0.99,提取的三角波环流有效地抑制了输入电流谐波,提高了整流器的功率因数。

图7 环流提取前后整流器的输入电压和电流Fig.7 Input voltage and current of rectifier with or without circuiting current
图8为环流提取电路的输入、输出电压和电流波形,环流提取电路的输入电压us和电流is为同相位的三角波,其从主电路吸收的功率为93 W,不到整流器输出功率的10%;环流提取电路的输出电流ips方向为正,这表明环流提取电路将提取的谐波能量回馈给了双反星形整流器负载,避免了谐波浪费。

图8 环流提取电路的输入和输出波形Fig.8 Input and output waveforms of circuiting current extraction circuit
图9比较了原双反星形整流器和提出的双反星形整流器在不同负载电流时的直流输出电压。

图9 环流提取前后整流器的输出电压Fig.9 Output voltage of rectifier with or without circuiting current extraction
由图9可知,提出的双反星形整流器的直流输出电压略大于原双反星形整流器的输出电压,这表明提取的三角波环流消除了换相过程引起的输出电压降。整流器直流输出电压的减小,仅由整流器的线路和元件阻抗产生。
图10比较了原双反星形整流器和提出的双反星形整流器在不同负载电流时的输入电流THD。
由图10可知,提出的双反星形整流器的输入电流谐波明显小于原双反星形整流器的输入电流谐波,且能在较大负载范围内使得输入电流的THD维持在5%以内,这表明提取的环流有效地抑制了双反星形整流器的输入电流谐波。

图10 环流提取前后整流器的输入电流THDFig.10 Input current THD of rectifier with or without circuiting current extraction
4 结论
本文提出了一种近似零电流换相的低谐波双反星形整流器,通过对该整流器的深入分析得到以下结论:
a.该整流器不仅能有效抑制输入电流谐波,而且整流器工作在近似零电流换相状态,整流器的输入输出特性同时得到改善;
b.提出的双反星形整流器按照二次换相的新模式进行换相,尽管二次换相的换相重叠角不为零,但其产生的换相压降恒为零,这与传统的整流器换相理论不同;
c.相同电路参数时,与传统的双反星形整流器相比,提出的双反星形整流器的换相重叠角显著减小,换相压降被完全消除;
d.该方案不仅能够获得较好的输入输出特性,而且电流注入电路的容量不到系统输出功率的10%,不会给原整流器带来大的体积、容量和成本的增加,在大功率场合具有良好的应用前景。
[1]王兆安,杨君,刘进军,等.谐波抑制和无功功率补偿[M].北京:机械工业出版社,2006:10-19.
[2]DAS J C.Passive filters-potentialities and limitations[J].IEEE Transactions on Industry Applications,2004,40(1):232-241.
[3]陈国柱,吕征宇,钱照明.典型工业电网谐波及其混合有源滤波抑制[J].电网技术,2000,24(5):59-63.CHEN Guozhu,LÜ Zhengyu,QIAN Zhaoming.Power harmoincs of industry and its suppression with hybrid active filter[J].Power System Technology,2000,24(5):59-63.
[4]陆翔,谢运祥,桂存兵,等.基于无源性与滑模变结构控制相结合的 VIENNA 整流器控制策略[J].电力自动化设备,2014,34(10):110-115.LU Xiang,XIE Yunxiang,GUI Cunbing,et al.VIENNA rectifier control strategy based on passivity control and sliding mode variable structure control[J].Electric Power Automation Equipment,2014,34(10):110-115.
[5]吴凯,程启明,李明,等.具有V2G功能的电动汽车快速充放电方法[J].电力自动化设备,2014,34(2):30-34.WU Kai,CHEN Qiming,LI Ming,et al.Fast charging and discharging method for electric vehicle with V2G function[J].Electric Power Automation Equipment,2014,34(2):30-34.
[6]邹高域,赵争鸣,袁立强,等.双PWM变换器的系统安全工作区及其应用[J].电力自动化设备,2014,34(3):82-88.ZOU Gaoyu,ZHAO Zhengming,YUAN Liqiang,et al.Systematic safe operating area of dual-PWM converter and its application[J].Electric Power Automation Equipment,2014,34(3):82-88.
[7]SINGH B,GAIROLA S,SINGH B N.Multipulse AC-DC converters for improving power quality:a review[J].IEEE Transactions on Power Electronics,2008,23(1):260-281.
[8]孟凡刚,杨世彦,杨威.多脉波整流技术综述[J].电力自动化设备,2012,32(2):9-22.MENG Fangang,YANG Shiyan,YANG Wei.Overview of multipulse rectifier technique[J].Electric Power Automation Equipment,2012,32(2):9-22.
[9]YANG Shiyan,MENG Fangang,YANG Wei.Optimum design of inter-phase reactorwith double-tap-changerapplied tomultipulse diode rectifier[J].IEEE Transactions on Industrial Electronics,2010,57(9):3022-3029.
[10]CHOI S,ENJETI P N,LEE H H,et al.A new active interphase reactor for 12-pulse rectifiers provides clean power utility interface[J].IEEE Transactions on Industry Applications,1996,32(6):1304-1311.
[11]BIELA J,HASSLER D,SCHONBERGER J,et al.Closed-loop sinusoidalinput-currentshaping of12-pulse autotransformer rectifier unit with impressed output voltage[J].IEEE Transactions on Power Electronics,2011,26(1):249-259.
[12]VILLABLANCA M E,NADAL J I,BRAVO M A.A 12-pulse AC-DC rectifier with high-quality input/output waveforms[J].IEEE Transactions on Power Electronics,2007,22(5):1875-1881.
[13]ARAUJO-VARGAS I,FORSYTH A J,CHIVITE-ZABALZA F J.Capacitor voltage-balancing techniques for a multipulse rectifier with active injection[J].IEEE Transactions on Industry Applications,2011,47(1):185-198.
[14]BAI Sanzhong,LUKIC S M.New method to achieve AC harmonic elimination and energy storage integration for 12-pulse diode rectifiers[J].IEEE Transactions on Industrial Electronics,2013,60(7):2547-2554.
[15]YOUNG C M,WU S F,YEH W S,et al.A DC-side current injection method for improving AC line condition applied in the 18-pulse converter system[J].IEEE Transactions on Power Electronics,2014,29(1):99-109.
[16]CHEN Qianhong,MAO Lang,REN Xiaoyong,et al.Research of the current-injection-based P-type 12-pulse ATRU [C] ∥2012 IEEE 7th International Power Electronics and Motion Control Conference.Harbin,China:IEEE,2012:41-46.
[17]RODRIGUEZ J,PONTT J,SILVA C,et al.Large current rectifiers:state of the art and future trends[J].IEEE Transactions on Industrial Electronics,2005,52(3):738-746.
[18]姚广,蒋大明.双反星形整流电路在电解中的应用[J].电力自动化设备,2006,26(10):54-56.YAO Guang,JIANG Daming.Application of double inverse star rectifying circuit in electrolysis[J].Electric Power Automation Equipment,2006,26(10):54-56.
[19]AQUEVEQUE P E,WIECHMANN E P,BURGOS R P.On the efficiency and reliability of high-current rectifiers[C]∥Proceedings of IEEE 41st IAS Annual Meeting.Tampa,USA:IEEE,2006:4509-4516.

