基于模糊元胞自动机的电网连锁故障控制策略

于 群，张 敏，曹 娜，贺 庆，石 良，易 俊

（1.山东科技大学 电气与自动化工程学院，山东 青岛 266590；2.中国电力科学研究院，北京 100085）

0 引言

近年来，国内外电力系统发生了多次连锁故障导致的大停电事故，给当今高度依赖电力的社会带来了巨大损失［1-6］。连锁故障机理研究表明，虽然各类连锁故障表现形式各异，但多数故障都是从系统个别元件发生故障开始，继而事故扩大引发多个元件过载并被切除，此时若不及时采取措施，将会导致局部甚至全网功率不平衡、潮流大范围转移，引发大量线路跳闸，系统发生振荡甚至解列，从而发生大停电事故［7-10］。

一般大停电事故可分为起始、扩大和崩溃3个阶段，从以上连锁故障的发展过程来看，如果要避免大停电的发生，对事故扩大阶段的控制最为关键。在此阶段，如果能够采取诸如通过稳控装置来切机、切负荷限制输电断面潮流等措施，就可以将事故限制在有限区域内，避免全网崩溃。《电力系统安全稳定控制技术导则》［11］给出了在电网紧急情况下的切除发电机、汽轮机快速控制汽门、切负荷、并联电容器强行补偿等控制手段，但这些手段实施的时机在《电力系统安全稳定控制技术导则》中并没有明确给出。文献［12］主要研究切负荷地点和切负荷量一定的条件下，切负荷时刻对系统稳定性的影响及最佳切负荷时刻的计算问题，并根据实际算例进行验证；文献［13］建立了基于贝叶斯网络的连锁反应故障概率分析模型，根据系统故障发展过程中连锁故障搜索和分析情况，提出以连锁故障风险最小为目标的预防控制方法；文献［14］将博弈思想应用于连锁故障的预防，将电网扰动作为对弈的进攻方，系统调整作为被动的防御方，计及不同类型的电网扰动作用，提出切负荷量最小的连锁故障预防控制策略，上述文献虽然都在不同方面就切机、切负荷控制措施展开了深入研究，但是并没有全面考虑控制措施使用时刻、位置及调整量这些重要因素。

考虑到在连锁故障的发展过程中，电网从正常状态转变为警戒、紧急等状态时的界限并不明显，本文首先将模糊理论引入电网故障元胞自动机（CA-power failure）模型中［15］，建立了基于模糊元胞自动机的电网故障FCA（Fuzzy-CA-power failure）模型，并给出了无功补偿、集中切负荷预防控制措施使用时间、位置及调整量的相关规则；最后通过在IEEE 39节点系统进行事故演化过程仿真，验证了电网的自组织临界特性［16-18］，并对控制措施加入前后的仿真结果进行对比，进一步验证了控制措施的有效性和可行性。

1 基于模糊元胞自动机的电网故障模型

1.1 电网元胞自动机

元胞自动机［19-20］是定义于一个离散元胞空间之上并且遵循相关的局部更新规律、随着时间的变化不断演变的一种系统。本文构造的电网故障元胞自动机模型如图1所示。

图1所示模型将电网进行抽象化，每个元胞代表1个电网元件（如线路、变压器等），与其直接相连的元胞即为其邻居元胞，所有元胞的集合组成一个元胞空间（所有的电网元件）。通过给每个元胞赋予一定的初始过载能力来模拟整个电网的原始情况，在电网故障的演化过程中，用元胞破裂来模拟元件发生故障，并用一定的数学函数来表示元件对故障的传递，即故障元件对非故障元件的影响。

图1 电网元胞自动机模型Fig.1 CA model of grid

1.2 模糊规则库的建立

模糊规则库［21］的建立应首先结合研究对象的特点选择适当个数的关键量作为输入变量，然后确定论域并分割模糊输入量的子集以及分布函数类型（按照实际情况选取符合认识和判断事物习惯的隶属函数，本文采用三角形分布隶属度函数），进而得到模糊输出量。

对电网故障演化过程进行仿真，本文主要考虑3个因素：电网元件（元胞）状态、电网（元胞机）状态和故障传递程度值。

a.电网元胞的状态模糊化。

在仿真实验中，一个电网元胞是否功能失效或产生故障，取决于其负载率的大小。定义电网元胞i在t时刻的负载率为：

其中，Pi为在t时刻流过电网元胞i的有功潮流绝对值；Pi，max为电网元胞i的最大允许传输容量。

为了更加精确地描述电网元胞状态，引入元胞状态L这一模糊变量，并根据负载率大小将L进行更精确的划分。负载率l的基本论域为［0，∞），根据已有的电网元件过载理论将连续的l分别取论域为l1=｛0，1.1｝、l2=｛1.1，1.3｝、l3=｛1.3，∞｝，那么 l的模糊子集定义为 l=｛l1，l2，l3｝，对应模糊输出量 L=｛L1，L2，L3｝=｛正常，紧急，故障｝，简记为｛N，U，F｝，则元胞状态 L在负载率l取值范围内的隶属度函数曲线及其分布如图2所示。

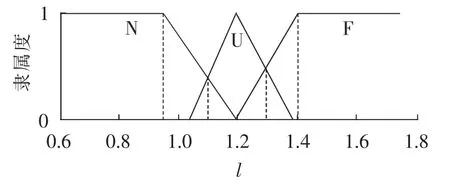
图2 电网元胞状态隶属度函数Fig.2 Membership function of grid cellular state

b.电网元胞机状态的模糊化。

《电力系统安全稳定控制技术导则》中，将电力系统的运行状态分为正常、警戒、紧急、极端紧急和崩溃等几种。参照这一划分方法及“随着扰动增加，元件负载率分布曲线斜率绝对值越来越大，当斜率增加到一定程度时，任何微小扰动都会导致停电事故的发生，此时系统处在自组织临界状态”的结论［22］，记负载率分布曲线经线性拟合后的斜率为k，电网元胞机状态为S，k的基本论域为（-∞，0］，参考多次仿真所得结果将连续的k分别取论域k1=｛-∞，0.3｝、k2=｛-0.3，-0.2｝、k3=｛-0.2，0｝，那么 k 的模糊子集定义为 k=｛k1，k2，k3｝，对应模糊输出量 S= ｛S1，S2，S3｝=｛正常，紧急，极端紧急｝，简记为｛N，U，VU｝，则电网状态S在负载率分布曲线斜率绝对值k取值范围内的隶属函数曲线及其分布如图3所示。

图3 电网状态隶属度函数Fig.3 Membership function of grid state

c.邻居元胞故障传递模糊化。

一个元胞破裂以后，势必会对其邻居元胞产生影响，本文定义其影响为：一个元胞破裂后影响其邻居的容量传输极限，使其减小，减小的值取决于此时电网状态S及破裂元胞在故障前一刻所处状态L，为了准确描述故障元胞对其邻居的影响，引入故障传递程度值R这一模糊变量，并根据此时电网元胞机状态S及破裂元胞故障前一刻的状态L将R分为5 个模糊子集合：R=｛VS，S，M，B，VB｝=｛很小，小，中，大，很大｝。R的模糊推理规则如表1所示。

表1 故障传递程度Table 1 Failure spreading degrees

d.线路过负荷保护动作模型。

电力系统继电保护中测量值和触发值误差会导致保护动作的不确定性，该不确定性使得恒定的故障率模型无法准确描述当前运行条件对电力设备的影响，于是本文引入基于传输潮流的线路停运概率模型，对电网元件运行状态的转换进行判断。

线路停运概率模型将线路过负荷保护动作模型简化成折线模型，如图4所示，纵坐标p表示线路j断开的概率，横坐标li表示元件i的负载率。

2 预防控制措施及其应用

2.1 预防控制措施

图4 线路停运概率模型Fig.4 Probability model of line outage

电力系统事故发展过程中电网逐渐趋于不稳定，整个过程中伴随着个别电网元件负载率的增加及传输无功功率的增大，在大停电之前（即紧急状态）采取有效的控制措施，将突然变化的量在电网正常运行的前提下最大限度地调节到变化前一状态，能有效减少电网连锁故障的发生。以此为基本思路，结合FCA模型，本文基于IEEE 39节点系统在元胞机状态紧急的情况下对无功潮流突变的元胞进行无功补偿，且对紧急状态元胞潮流流入方向所在母线节点采取集中切负荷的控制措施，以减少大停电发生的次数及规模。

a.切负荷规则。

对于单一的电网元胞（主要考虑线路），随着故障的演化个别元胞传输潮流急剧增大，由正常逐渐向紧急和故障状态演化，故障元胞又会对其邻居元胞进行故障传递，依次演化，最终导致元胞机大范围停运，即电网连锁故障发生。为了减小元胞潮流增大对元胞机正常运行的影响，本文对上述元胞潮流流入方向所在节点采取集中切负荷的控制措施。线路有功潮流传输如图5所示。

图5 线路有功潮流传输Fig.5 Active power flow transmission of line

对元胞 i，传输的有功功率为 Pi，则 li=Pi／Pmax。设元胞i在状态演化过程中，传输功率由Pi1（正常）增大到Pi2（紧急）（故障状态时线路断开，不做考虑）。为了减小元胞i传输的功率，在元胞机处于紧急状态时对潮流流入方向的母线节点BT采取集中切负荷的控制措施，切除的负荷量为ΔP，切除负荷后，元胞尽可能回到正常状态，即负载率 li∈（0.7，1）。

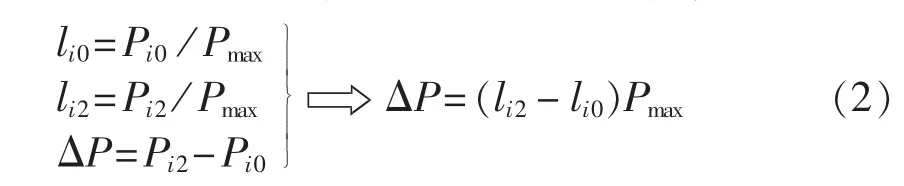
其中，li0为元胞i的期望负载率；Pi0为传输功率期望值；li2为元胞i在紧急状态时的负载率。

b.无功补偿规则。

电网事故传播过程中潮流重新分配，无功潮流分布逐渐趋于不平衡，个别元胞（主要考虑线路）所传输的无功潮流突然发生大幅变化，该变化将会导致节点电压不稳定甚至元胞机停运、电网崩溃。为了减小无功潮流突变对元胞机正常运行的影响，本文在检测到元胞i所传输的无功潮流变化较大时即对该元胞采取无功补偿的预防控制措施。线路无功补偿如图6所示。

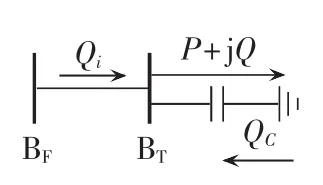
图6 线路无功补偿Fig.6 Reactive power compensation of line

一次事故演化过程中若元胞i传输的感性无功功率Qi突然增大（此处认为大于初始值的1.5倍为突然增大，具体数值可根据实际情况进行调整），为了减小无功突变对元胞机稳定运行的影响，当元胞机处于紧急状态时在元胞i无功潮流流入方向的母线节点BT处利用电容器进行无功调整，补偿量为QC（见式（3））。反之，若元胞i传输的感性无功功率Qi突然变为容性无功，为了减小该变化对元胞机稳定运行的影响，当元胞机处于紧急状态时在元胞i无功潮流流出方向的母线节点BF处利用电抗器进行无功调整，补偿量为 QL（见式（3））。

若系统中所有容性补偿量用完后仍存在无功缺额，并且节点电压低于额定允许电压的下限，则此时将会因为无功不足引起电压崩溃问题，此时应选择重载的元胞进行主动切负荷处理，并确认系统发生了事故。

2.2 结合预防控制措施的元胞自动机转换规则

将以上预防控制措施的基本思路应用到基于模糊元胞自动机的电网故障模型中，即元胞机处于紧急状态时对其所在母线节点采取切负荷的控制措施，且对无功潮流突变的元胞采取无功补偿的控制措施；同时利用线路停运概率模型和故障传递模型决定元胞下一时刻的状态及故障元胞对其邻居的影响。根据这种思路，本文设定了元胞的演化更新规则如下。

a.t时刻：根据线路停运概率模型（图4）及元胞负载率隶属度函数（图2）确定各元胞状态（正常、紧急、故障），若元胞处于故障状态，则根据故障传递模糊控制规则库进行故障传递。

b.t+1时刻：根据当前元胞机状态及各元胞潮流相应采取切负荷（式（2））和无功补偿（式（3））控制措施，再次进行潮流计算，根据线路停运概率模型及元胞负载率隶属度函数完成元胞状态的更新。

3 基于电网故障模型的仿真实验

3.1 仿真流程

为了验证上述预防控制措施的有效性，搭建基于模糊元胞自动机的电网故障模型，并结合控制措施进行电网故障仿真。仿真实验采用MATLAB R2011b软件编程实现。仿真过程如下。

a.获得各元胞的潮流传输极限Pmax及初始无功潮流。

b.随机选择一个节点，增加负荷扰动ΔD，通过牛顿法求解电网潮流。

c.根据电网潮流得各线路负载率，按上述电网状态模糊控制规则库判断电网状态。

CaseⅠ：电网状态为正常，对电网中所有元胞进行扫描式检测。若各元胞经停运概率模型检测后仍正常运行，则不采取任何控制措施；否则元胞为故障状态，转步骤d。

CaseⅡ：电网状态为紧急，首先根据无功补偿控制措施调整个别元胞的无功，然后对电网中所有元胞进行扫描式检测。若各元胞经停运概率模型检测后仍正常运行，则判断该元胞状态，若元胞为正常状态，则不采取任何控制措施，若元胞为紧急状态，则采取集中切负荷的控制措施；否则元胞故障，转步骤d。

CaseⅢ：电网为极端紧急状态，系统解列，转步骤f。

d.切除故障元胞并根据故障传递模糊控制规则库进行故障传递。

e.判断电网是否因元胞失效而有负荷点被切除进而形成孤岛或系统解列，如有则转步骤f；否则转步骤b。

f.统计损失负荷，一次故障演化结束。

重复以上步骤100次，其实验流程图如图7所示。

3.2 一次故障演化过程仿真

利用上述构造模型在IEEE 39节点系统上进行仿真，在仿真过程中，每增加一次扰动，计算出各元件负载率后按由大到小排序，在双对数坐标图中绘出其分布曲线，观察随着扰动的增加负载率分布曲线的变化情况。根据已有理论基础及仿真经验，假设电网中各元件初始负载率在区间［0.55，0.95］内随机分布，一次事故演化过程中，负载率分布曲线如图8所示（图中横轴取值为元胞序列号的双对数值），其一次事故演化的仿真过程如图9所示（图中虚线表示在不同时间内断开的线路）。

初始状态下，元件负载率在给定区间内随机分布，其分布曲线的斜率 k为-0.1566，如图8（a）所示；持续随机选择负荷节点增加负荷扰动，部分线路元件的负载率增大，则元件负载率分布曲线斜率绝对值增大，直到电网由正常状态演化为紧急状态，如图8（b）所示，此时 k=-0.1702；继续增加扰动，当演化达到一定程度（图8（c）），线路4-5所传输的感性无功突变为容性无功，则利用电抗器进行无功调整，QL=2.06 p.u.，此时 k=-0.1731；随着扰动的增加，处于紧急状态的电网进一步演化，当k=-0.1781（如图8（d）所示）时，线路15-16由正常状态转换为紧急状态，此时对节点15采取切负荷的控制措施，ΔP=0.828p.u.；然后，电网演化为图8（e）的状态，此时 k=-0.1876，线路 14-15过载断开，线路 13-14、23-24所传输无功功率大幅度增大，则利用电容器进行无功调整，分别取 QC=14.186 p.u.、QC=1.621 p.u.，同时线路17-27由正常状态转换为紧急状态，此时对节点27采取切负荷的控制措施，ΔP=15.267p.u.；持续增加扰动，电网进入极端紧急状态，如图8（f）所示，此时k=-0.3593，线路8-9、9-39相继过载断开，电网解列为两部分（图9），一次故障演化结束。

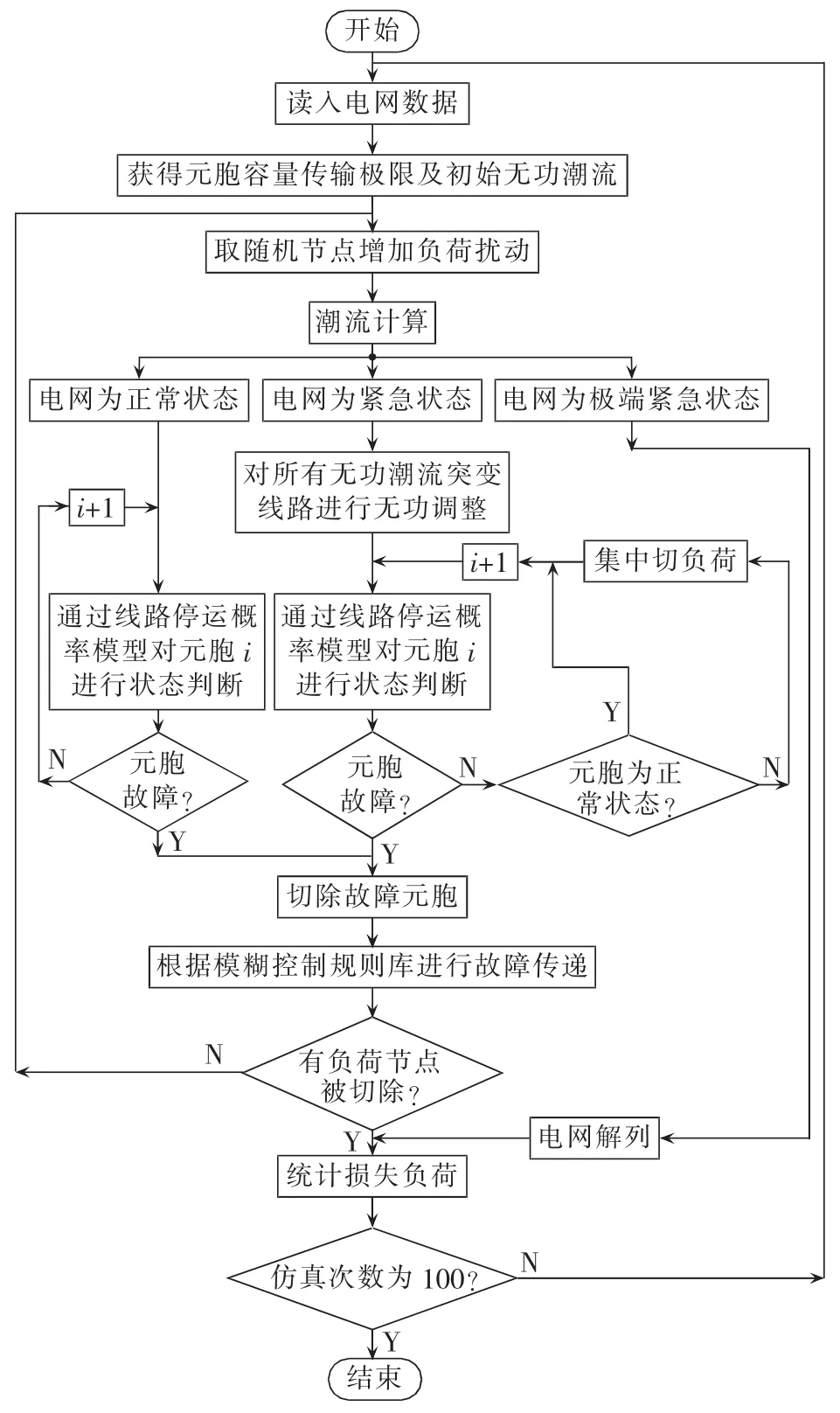
图7 仿真流程图Fig.7 Flowchart of simulation

3.3 仿真结果分析

为了验证上述控制措施在电网演化过程中的作用，基于IEEE 39节点系统，对上述FCA模型分别进行不添加控制措施及添加控制措施后的电网故障仿真模拟各100次，得到故障发生时损失负荷的故障时间序列及损失负荷的标度频度幂律曲线。

2种情况下的故障时间对比如图10所示。

由图10可知，按照上述控制规则添加控制措施后，电网模型发生100次故障时所承担的扰动次数大约为7000次，远大于不添加控制措施时模型所承担的扰动次数。假设以上扰动在电网中每天发生一次，即电网发生100次大停电事故的天数由4300 d（图10（a））延长至 7000d （图10（b）），极大地提高了电网的稳定性。

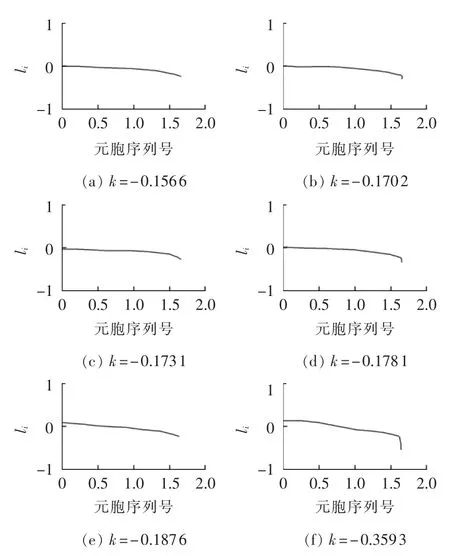
图8 一次事故演化过程中各元件负载率的变化Fig.8 Variation of element load rate during failure evolution

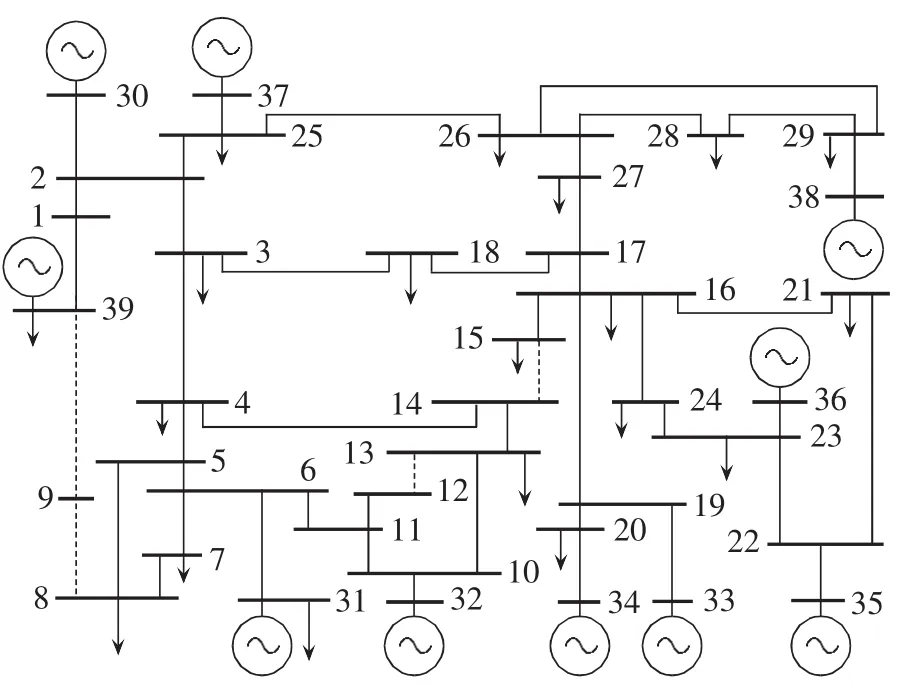
图9 基于IEEE 39节点系统事故演化过程Fig.9 Failure evolution process of IEEE 39-bus system

添加控制措施前后的损失负荷幂律曲线如图11所示。由图11可知，添加控制措施后，拟合曲线斜率绝对值明显增大，电网更加稳定；且同等故障次数中，产生较大损失负荷的故障次数较控制措施使用前明显降低（标度＞3区域）；同时，损失负荷规模较控制措施使用前维持在同等水平。

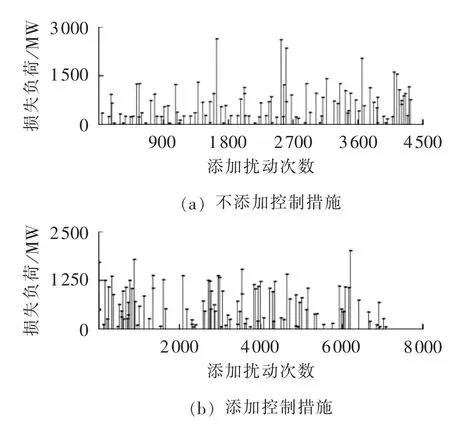
图10 采用控制策略前后的故障时间序列图Fig.10 Time sequential diagram of failure between with and without control strategy

图11 添加控制措施前后损失负荷幂律曲线对比Fig.11 Comparison of load-loss power law curve between with and without control strategy

综上所述，控制措施的增加，一方面使电网故障发生的时间间隔大幅度延长，降低了电网事故发生的频率；另一方面故障规模较控制措施使用前没有上升，且损失负荷幂律曲线斜率绝对值增大，产生较大规模损失负荷的故障次数明显减少，极大地提高了电网的稳定性，验证了上述控制措施的有效性。文献［12-14］虽然都在不同方面就切机切负荷控制措施展开了深入研究，但是并没有全面考虑控制措施使用时刻、位置及调整量这些重要因素，本文基于模糊元胞自动机的电网控制措施的使用，在考虑上述重要因素的基础上达到了减小电网故障发生规模及频率的目的。

4 结论

本文考虑初始故障后元件及电网运行状态的变化和故障线路对其邻居的故障传递，结合模糊理论和元胞自动机理论构造基于模糊元胞自动机的电网故障模型，并基于潮流传输原理提出连锁故障演化过程中降低停电事故的切负荷控制规则和无功补偿控制规则，最后完成基于IEEE 39节点系统的停电事故仿真，仿真结果首先验证了模型的有效性，进而通过对控制措施加入前后仿真结果的对比发现：控制措施的使用使得FCA模型发生100次故障所承担的扰动次数大幅度增加，即电网事故发生的时间间隔变大；同时损失负荷幂律特性曲线斜率绝对值较控制措施添加前增大，电网更加稳定；同等的故障次数中，添加控制措施后发生较大损失负荷的次数减少，且损失负荷规模较控制措施使用前维持在同等水平，验证了控制措施的有效性和可行性。

［1］郭剑波.“八五”期间全国电网稳定事故统计分析［J］.电网技术，1998，22（2）：72-74.GUO Jianbo.Statistics and analysis of incidents bulk power system from 1991-1995［J］.Power System Technology，1998，22（2）：72-74.

［2］汤涌，卜广全，易俊. 印度“7.30”、“7.31”大停电事故分析及启示［J］. 中国电机工程学报，2012，32（25）：167-174.TANG Yong，BU Guangquan，YI Jun.Analysis and lessons of the blackout in Indian power grid on July 30 and 31，2012［J］.Proceedings of the CSEE，2012，32（25）：167-174.

［3］August 14，2003 blackout in the United States and Canada：causes and recommendations［EB／OL］. （2007-01-10）［2015-01-28］.http：∥www.nerc.com.

［4］薛禹胜.综合防御由偶然故障演化为电力灾难：北美“8.14”大停电的警示［J］. 电力系统自动化，2003，27（18）：1-5.XUE Yusheng.The way from simple contingency to system wide disaster：lessonsfrom theeastern interconnection blackoutin 2003［J］.Automation of Electric Power Systems，2003，27（18）：1-5.

［5］甘德强，胡江溢，韩祯祥.2003年国际若干停电事故思考［J］.电力系统自动化，2004，28（3）：1-4.GAN Deqiang，HU Jiangyi，HAN Zhenxiang.Pondering on the international blackouts of 2003［J］.Automation of Electric Power Systems，2004，28（3）：1-4.

［6］刁塑，刘俊勇，刘友波，等.考虑电网承载结构的连锁故障模拟与防御策略［J］. 电力自动化设备，2015，35（11）：143-150.DIAO Su，LIU Junyong，LIU Youbo，etal.Cascading failure simulation and defense strategy considering grid carrying structure［J］.Electric Power Automation Equipment，2015，35（11）：143-150.

［7］丁道齐.复杂大电网安全性分析［M］.北京：中国电力出版社，2010：136-161.

［8］石立宝，史中英，姚良忠，等.现代电力系统连锁性大停电事故机理研究综述［J］.电网技术，2010，34（3）：48-55.SHI Libao，SHI Zhongying，YAO Liangzhong，et al.A review of mechanism of large cascading failure blackouts of modern power system［J］.Power System Technology，2010，34（3）：48-55.

［9］丁明，韩平平.小世界电网的连锁故障传播机理分析［J］.电力系统自动化，2007，31（18）：6-10.DING Ming，HAN Pingping.Study of failure spreading mechanism in the small-world power grid［J］.Automation of Electric Power Systems，2007，31（18）：6-10.

［10］胥威汀，刘俊勇，李旻，等.避免电网连锁解列的全局协调控制策略［J］. 电力自动化设备，2013，33（3）：33-39.XU Weiting，LIU Junyong，LI Min，et al.Globally coordinated controlforpreventing cascading splitofpowersystem ［J］.Electric Power Automation Equipment，2013，33（3）：33-39.

［11］中华人民共和国国家经济贸易委员会.电力系统安全稳定控制技术导则：DL／T723—2000［S］. 北京：中国电力出版社，2000.

［12］袁宇春，张保会.最佳切负荷时刻的计算［J］.继电器，1999，27（6）：1-4.YUAN Yuchun，ZHANG Baohui.Calculating the optimal load shedding time［J］.Relay，1999，27（6）：1-4.

［13］付蓉，蒋国平，王保云.计及系统连锁故障风险的电网预防控制［J］. 电力系统保护与控制，2011，39（3）：12-17.FU Rong，JIANG Guoping，WANG Baoyun.A preventive control strategy for power grid considering system cascading failure risk［J］.Power System Protection and Control，2011，39（3）：12-17.

［14］朱旭凯，刘文颖，杨以涵.电网连锁故障演化机理与博弈预防［J］.电力系统自动化，2008，32（5）：29-33.ZHU Xukai，LIU Wenying，YANG Yihan.Evolution mechanism and preventing strategies for cascading failure［J］.Automation of Electric Power Systems，2008，32（5）：29-33.

［15］于群，曹娜，郭剑波.基于元胞自动机的电力系统自组织临界特性仿真模型［J］. 电力系统自动化，2011，35（21）：1-5.YU Qun，CAO Na，GUO Jianbo.Power system self-organized criticality simulation modelbased on cellularautomata［J］.Automation of Electric Power Systems，2011，35（21）：1-5.

［16］于群，郭剑波.我国电网停电事故自组织临界性的研究［J］.电网技术，2006，30（6）：1-5 YU Qun，GUO Jianbo.Study on self-organized criticality characters of power system blackouts in China［J］.Power System Technology，2006，30（6）：1-5.

［17］梅生伟，薛安成，张雪梅.电力系统自组织临界特性与大电网安全［M］. 北京：清华大学出版社，2009：144-164.

［18］BAK P，TANG C，WIESENFELD K.Self-organized criticality：an explanation of 1／f noise［J］.Physical Review Letters，1987，59（4）：381-384.

［19］DOBSON I，CHEN J S，THROP B A，et al.Examining criticality of blackouts in power system models with cascading events［C］∥Proceedingsofthe 35th AnnualHawaiiInternationalConference on System Sciences，2002. ［S.l.］：IEEE，2002：1-10.

［20］CHEN J，THORP J S.Study on cascading dynamics in power transmission systems via a DC hidden failure model［J］.Journal of Electrical Power and Energy System，2005，27（4）：318-326.

［21］刘新东，江全元，曹一家，等.基于风险理论和模糊推理的电力系统暂态安全风险评估［J］. 电力自动化设备，2009，29（2）：15-20.LIU Xindong，JIANG Quanyuan，CAO Yijia，etal.Transient security risk assessment of power system based on risk theory and fuzzy reasoning［J］.Electric Power Automation Equipment，2009，29（2）：15-20.

［22］郭剑波，于群，贺庆.电力系统复杂性理论初探［M］.北京：科学出版社，2012：25-58.