基于改进PCA与FLD算法的人脸识别
丁朔
摘要:该文研究人工智能中人脸识别的问题,由于受到光照以及人脸表情等各种因素的影响,论文中我采用的是改进的主成分分析算法(PCA)和Fisher LDA(FLD)算法相结合,使PCA算法具有灰度归一化的能力。首先将训练样本的人脸图像进行预处理,将每一张图片转换成一个列向量,最后所有的列向量合成一个矩阵。利用K-L变换提取一个低位特征空间来表示人脸图像,得到特征脸空间。在Fisher鉴别准则下,求一个最佳鉴别方向,从高位特征向量投影到最佳鉴别方向上构成一个鉴别特征空间,训练样本获最佳描述特征,然后将特征脸空间降维,得到各类人脸特征库,接着将待识别的人脸进行PCA降维以及通过FLD分类器,在特征脸数据库中寻求与该人脸欧氏距离最近的人脸图像。该文算法是用人脸数据库进行测试。最终确定本论文的方案切实可行,能够将人脸的各种表情以及图片缺失或者重组等特殊情况均可识别并匹配。
关键词:改进的PCA算法;FLD算法;K-L变换;最佳描述特征
中图分类号:TP311 文献标识码:A 文章编号:1009-3044(2016)08-0164-02
1 算法
本课题的思想是在人脸识别过程中,光照对于识别率的影响很大,为了克服光照条件对于特征值即特征空间的影响,我们对主成分分析法PCA算法进行改进,使其具有灰度归一化的能力然后将其与Fisher LDA方法相结合,克服人脸识别过程中光照对于识别目标的影响,进一步提高人脸识别的准确率。
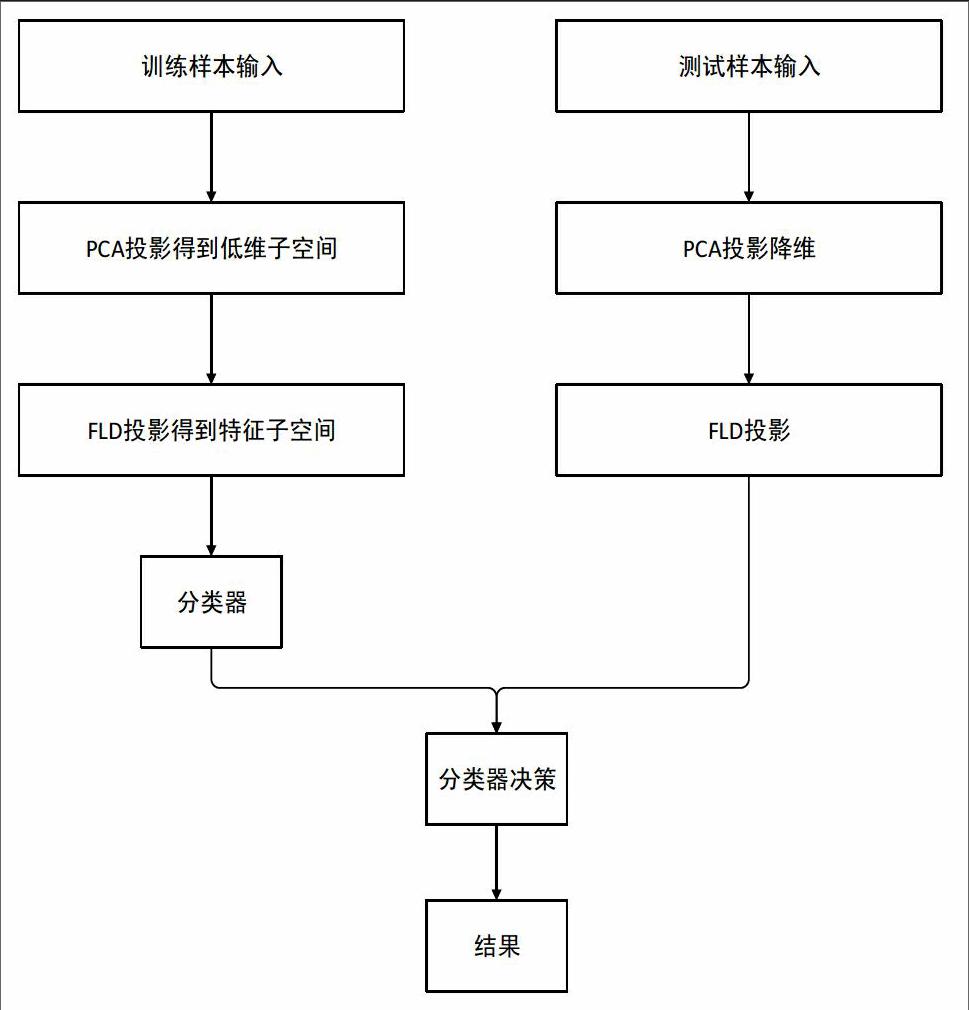
首先处理样本训练库,利用K-L变换提取低位特征空间,然后利用主成分分析法PCA提取已定位的人脸区域得到人脸特征,从而得到特征脸空间。Fisher线形判别方法(FLD)是在Fisher鉴别准则函数去极值的情况下,求得一个最佳鉴别方向,然后从高位特征向量投影到该最佳鉴别方向上构成一个一维的鉴别特征空间。将Fisher线性判别推广到C-1个判决函数下,即:从N维空间向C-1维空间作相应的投影,利用这个投影矩阵将训练样本转化为MEF空间并且获得最佳描述特征,然后求出类内散布矩阵与类间散布矩阵,取K个最大的特征构成FLD投影矩阵,将最佳描述特征在FLD矩阵上投影,获得最佳分类特征。然后将特征脸空间降维,接着对每个类的典型样本进行投影,得到各类样本的投影特征得到该人脸特征库,最后将待识别的人脸进行PCA降维以及FLD分类器,在特征脸数据库中寻求与该人脸欧氏距离最近的人脸图像。
2 流程图
3 步骤
3.1 训练人脸库的数据处理
训练的人脸库中共有P张M*N大小的人脸图,将每一张图片转换成一个列向量,最后P个列向量合成一个M*N行P列的矩阵T。
3.2 特征脸的计算以及特征向量的选取
一幅大小为X*Y的图像可表示为n(n=x*y)维空间中的一个点,这个点的坐标对应着原图中的一个图像单元或者称为像素。如果样本空间共有M幅图像,那么这M幅图像对应于n维空间中的M个点,由于都是人类图像,所以在图像空间中是相互聚集在一个较近的邻域中,我们利用K-L变换提取一个低位特征空间来表示每幅人脸图像,从而得到特征脸空间。
得到由特征脸组成的降维子空间W后,每幅图像向其投影,获得的坐标系数即为该图像在该子空间的位置也就是该同学通过PCA变换的展开系数,即:该图像的代数特征,用于人脸识别的依据。因此在获得特征脸空间后,通过对每个类的典型样本进行投影,得到各类样本得到投影特征得到该人脸特征库作为接下来匹配和识别的搜索空间。
步骤如下:
(1) 计算样本差图:[f=f-X]
(2) 在特征子空间上进行投影:[y=WTf]其中[W=[w1,w2…wm]]
(3) 将y在特征搜索空间进行匹配,以与特征自空间中最短欧式距离以及人脸阈值作为匹配准则。降维后维数减少,但实际应用中不是每一个特征向量都有保留的意义,在PCA运算中,我们通常选取前m个特征值最大的特征向量,使得贡献率[e=i=1mλii=1Mλi≥0.99]。
3.3 学习过程
(1) 假设有M个N维训练样本的c类人脸库[Xij(i=1,2,3...cj=1,2,3...m)],[Xij]表示第i类别的第j个标本,利用改进的PCA算法经过灰度归一化的样本协方差矩阵进行计算,最后得到PCA变换矩阵。
(2) 通过PCA变换矩阵将训练样本集降维,转化为MEF空间并提取最佳描述特征。
(3) 计算由训练集最佳描述特征向量构建的类内散布矩阵[Sw]和类间散步矩阵[Sb],计算[Sw-1Sb]的C-1个最大特征值对应的特征向量,构成FLD变换矩阵。
(4) 通过FLD变换矩阵将MEF空间转换为K维的最佳鉴别特征空间,并获得最佳鉴别分类特征,根据分类特征构成人脸特征数据库。
3.4 目标识别
(1) 将某个待识别的目标样本人脸图片X通过PCA变换得到m维空间中的最佳特征描述向量。
(2) 对最佳描述特征向量进行FLD变换得到线性空间最佳分类特征向量。
(3) 寻找到和目标样本欧氏距离最近的特征数据库中的人脸进行识别。
4 评价与展望
PCA算法是无监督学习法,属于自动聚类,一旦偏离方向会产生非常大的错误;同时Fisher线性判别法属于监督学习,但人脸识别属于高维小样本的问题,所以投影矩阵进行降维后容易造成类内散步矩阵奇异。为了得到最佳的鉴别向量,本课题的解决方案是基于改进的主成分分析法PCA算法与Fisher线性判别相结合的方案,该方案比单纯使用PCA算法或者FLD算法的识别效果都要好,利用人脸数据库进行测试,最终确定本文算法的识别率较高。缺点就是样本训练时间和计算时间都一般,改进的PCA算法具有灰度归一化的能力,能够克服光照对识别人脸的影响,但本解决方案仍然有待改进的地方,例如:未达到实际应用要求的样本训练时间以及计算时间、人脸的校准问题、年龄问题、遮掩等问题进行研究,进一步找到更有效的人脸识别方式。

