“均值”的延拓式教学设计

杨湘豫

(湖南大学 数学与计量经济学院,长沙 410082)



“均值”的延拓式教学设计

杨湘豫

(湖南大学 数学与计量经济学院,长沙 410082)

摘 要:对概率论与数理统计课程中的 “均值”的教学,教师不仅要训练学生对“均值”的计算能力,而且要重视学生理解“均值”的实际意义以及相关知识的拓展方面的教学.本文针对“均值”概念及其运用的教学环节,给出了与“均值”相关联的其它的“数字特征”的延拓式的教学设计.

关键词:均值; 数字特征; 延拓式; 教学设计

1　延拓性教学方法的含义及意义

延拓性教学,它不是局限于对某个知识点的一般含义的独立讲解,而是将该知识点的认知拓展到与其联系着的其它知识点,使学生能够对掌握的知识举一反三,养成思考式的主动学习的习惯,学生不再是知识的被动接受者.延拓性教学方法极大地提升了学生的分析问题与解决问题的能力.笔者在近30年的概率论与数理统计课程的教学过程中,一直采用启发式及延拓式的教学方法,学生学习的热情大大提高.以下是笔者对“均值”这一知识点的延拓式教学设计.

2　“均值”(或“数学期望”)的教学设计

2.1 “数学期望”的定义

我们采取易于理解的直观教学方式,从n个数的算术平均入手,给出离散型随机变量X的均值(或数学期望)的概念.同时比较算术平均与随机变量X的均值的区别,以更好地理解数学期望的意义.

离散型的随机变量的情形[1].

连续型的随机变量的情形.

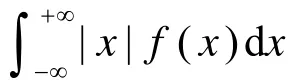
为连续型的随机变量的的数学期望.

由随机变量的数学期望的概念,不难获得由数学期望延拓的随机变量的数字特征.

2.2 方差Var(X)(或D(X))的刻画

Var,即方差(Variance),是概率统计中一个非常基础的重要概念,用于表示随机变量相对于其平均值(即数学期望)的偏离程度,已被广泛地应用到许多实际问题的分析中.[X- E(X)]称为随机变量X的离差,利用离差的平方来刻画随机变量X偏离其数学期望的E(X)的程度.

方差Var(X)的表达式为

从方差Var(X)的表达式可知,方差是离差平方的期望,属于期望的范畴.

2.3 协方差及相关系数的意义

数学期望E(X)、E(Y)反映随机变量X及Y各自的均值,Var(X)、Var(Y)反映随机变量X及Y各自偏离其数学期望的程度.当论及随机变量X及Y的相互关系时,就需要知道协方差及相关系数的概念.协方差在一定程度上反映了X与Y之间的关系,但它受到度量单位的约束.为了克服这一缺陷,将协方差标准化,即可得相关系数ρXY.相关系数ρXY刻画了X与Y之间的线性相关程度.

从协方差Cov(X ,Y)的表达式可知,协方差是两个随机变量X及Y离差之积的期望,也属于数学期望的范畴.

设随机变量X、Y ,且Var(X)＞ 0,Var(Y)＞ 0,则称X*、Y*为随机变量X、Y的标准化随机变量,其表达式为

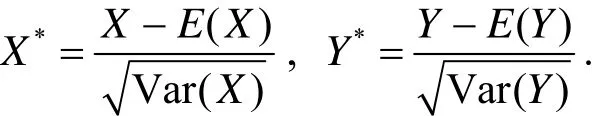
两个随机变量X及Y的相关系数为

从相关系数ρXY的表达式可知,相关系数是标准化随机变量的协方差,仍属于数学期望的范畴.

2.4 变异系数、偏度、峰度[2]、矩的解释

变异系数是用数学期望为单位去度量随机变量取值的波动程度,变异系数的定义式为

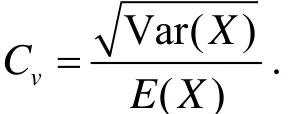
总体偏度为

(样本)偏度反映总体分布密度曲线的对称性信息.当样本偏度大于零时,分布形状右尾长(正偏); 当样本偏度小于零时,分布形状左尾长(左偏).

总体峰度为

(样本)峰度反映总体分布密度曲线在其峰值附近的陡峭程度的信息.当样本峰度小于零时,比正态分布来得平坦.峰度不是指概率密度的峰值高低.显然,变异系数、峰度、偏度的定义都是与“数学期望”相关联的.

另外,由矩[1](原点矩、中心矩、混合矩)的概念及运算知,它们也都归属于随机变量函数的数学期望.

3　方差(Var)的延拓及Var — VaR — VAR三者的比较

在风险投资及风险管理[3]的大量文献中,我们常常会遇见三个英文缩写Var、VaR和VAR的字样,乍看还以为它们是一样的,因为它们在形式上十分相似,但事实上,它们表达的含义却大为不同.

(1)Var,即方差(Variance),用于表示随机变量相对于其平均值(即数学期望)的偏离程度.Var概念广泛地应用于许多实际问题的分析中,比如,在讨论经济及金融时间序列的波动性问题时,常用方差来反映收益率的波动情况.由于方差法度量风险方便且实用性强,因此该方法是迄今为止最具影响和广泛应用的方法.

如果已知某一资产组合的波动程度,则可通过数据的处理得到其收益情况的平均波动.以方差衡量市场风险的公式为

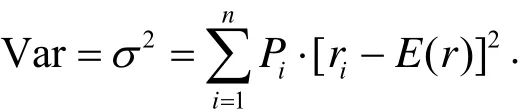
其中ir为资产的第i种收益率,iP是与该收益率相对应的概率.

方差有较好的统计性质,尤其当收益率服从正态分布时,资产组合的风险矩阵将更容易计算,可以利用独立资产的收益率方差和它们收益率之间的协方差得到.

用资产收益率的波动程度来描述风险虽然有一定道理,但只有收益率向下波动才可能带来损失,因此用方差来描述风险不能完全反映风险的经济意义.

(2)VaR(Value at Risk),即风险价值,它表示的是“处于风险中的价值”.VaR是利用统计学的思想度量风险,它的定义由Jorion[4]给出,简单描述为在一定持有时间内在给定置信区间下资产的最大可能损失值.VaR方法是风险管理和风险度量的主流方法.VaR表示的是资产或资产组合在市场常规波动情况下面临的最大损失价值.在给定时间内,对应于某一设定置信度(概率),资产或资产组合可能发生的最大损失价值,即

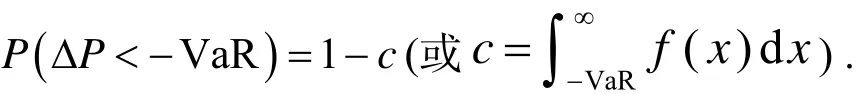
其中ΔP为资产组合在Δt时期内的损失,VaR是给定置信度c时的在险价值.

计算VaR的过程中要考虑五个因素,分别是资产持有时间、置信水平、数据的频度、价值函数和分布函数.这里,价值函数和分布函数是VaR计算的核心和难点.价值函数应用的是估值模型,该模型以资产价值与市场因子间的相互影响关系为依据而设定; 分布函数一般会用市场因子的波动性模型替代,是根据市场因子的未来分布确定的.通常要预先给定收益率的概率分布假定,重点在于对模型参数的计算.模拟方法可以直接根据模拟出的数据寻找分位数从而得到将要求解的风险值,这一过程常常是采用历史模拟法或蒙特卡罗模拟法实现的.

VaR方法克服了方差(Var)法的很多不足,直接将风险刻画为一个数字,不仅能满足投资者对损失的直观感受,也可以综合反映不同证券组合、不同市场部门的风险情况.但VaR方法仍有缺点,那就是当市场运行出现极端情况比如股市崩盘时,VaR方法不再适用[4],而且VaR没有次可加性,对此衍生出了改进方法CVaR.

(3)VAR,向量自回归模型[2](Vector autoregression),是根据数据的统计特性建立起来的模型.该模型以联立方程的形式构造出系统内每个内生变量对所有内生变量滞后值的函数,建立起对它们之间动态关系的估计,是现代宏观经济学的实证研究中的一种主流方法.

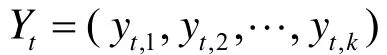
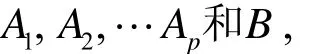
VAR模型的应用领域涵盖了房地产、股市等多个方面,在许多实证问题(例如中国货币供给决定、货币政策的有效性和中介目标的选择、潜在通货膨胀率的度量和通胀因素的分解等问题)中,都有非常重要的应用[5].

通过对Var、VaR和VAR三个概念的比较可知,Var(方差)和VaR是风险度量的两个不同工具,方差法在描述金融资产波动性方面有很重要的应用,因此可以方便快速地比较出几种资产的风险性; 而VaR方法可以给出具体的数值,解答在一定置信度下损失的最大值这一问题,更符合投资者对风险的感受.而向量自回归模型VAR在建立多个时间变量间的动态关系时有重要应用.

4　结论与展望

基于“数学期望”的延拓式教学方法的实践,只是笔者对概率论与数理统计课程教学中的点滴感悟.“数学期望”这种延拓式教学方法不仅对本课程的学习有益,而且可为后续课程的学习做好铺垫.

随着经济的飞速发展,社会的不断进步,我们必须从新的视角来认识数学的教学过程.数学的教学应该从目的、内容、形式、方法到组织进行全面改革,旨在使教学的表现形式更加形象化、多样化、视觉化,更有利于充分揭示数学的魅力及数学思维的作用.笔者在近30年的数学教学过程中,一直探寻着延拓性的教学方法,并一步一步地在实践着.笔者主持的已上线的国家视频公开课“经济生活的数学魅力”,采用了案例赏析的教学方式,从通俗易懂的例子切入,将数学知识延拓于我们的经济生活中.此课程获得了很好的社会反响.该课程团队在此视频课的基础上,不断改进并完善教学模式,又制作了“经济与数学”的慕课课程.我们继续在探索教学方法的路上前行,不断地寻求更加完善的教学方法.

参考文献

[1] 杨湘豫,罗 汉.大学数学4[M].北京: 高等教育出版社,2015

[2] 庞 皓.计量经济学[M].北京: 科学出版社,2012

[3] 王春峰.金融市场风险管理[M].天津: 天津大学出版社,2001

[4] Jorion.VaR: 风险价值[M].张海鱼,译.北京: 中信出版社,2000.

[5] 张延群.向量自回归模型的理论方法及应用实例[M].北京: 中国社会科学出版社,2013

Extension Type Teaching Design of " Mean"

YANG Xiang-yu
(College of Mathematics and Econometrics,Hunan University,Changsha 410082,China)

Abstract:On the teaching of " Mean " in the course "probability theory and mathematical statistics,teachers not only to train the computing power of students on “Mean”,but also to pay attention to the teaching about students' understanding on the practical significance of " Mean "and Extended type of the relevant knowledge.In this paper,aiming at teaching link of the concept of " Mean " and its application,the teaching design of the extension of the other " Digital feature " which is related to the " Mean " is given.

Key words:mean,digital feature,extended type,teaching design

作者简介:杨湘豫(1964−),女,湖南永州人,湖南大学数学与计量经济学院教授.主要研究方向: 金融数学及大学数学教育

基金项目:国家第七批视频公开课《经济生活的数学魅力》(教高厅函[2015]11号)

收稿日期:2015-10-05

中图分类号:G642

文献标识码:A

文章编号:1672-5298(2016)01-0079-04