基于时间Petri网的区间作业车间调度问题建模与分析

潘 理,杨 勃(湖南理工学院 信息与通信工程学院,湖南 岳阳 414006)



基于时间Petri网的区间作业车间调度问题建模与分析

潘 理,杨 勃
(湖南理工学院 信息与通信工程学院,湖南 岳阳 414006)

摘 要:区间作业车间调度问题近年来已成为生产调度研究的热点,现有研究工作主要集中于问题描述和优化求解方面,在理论模型、动态性质等方面还缺乏实质性成果.使用时间Petri网模型建模区间作业车间调度问题,并运用状态类可达性分析方法,分析模型所有可行调度,进而求解具有最小下界和最小上界的优化调度,为区间作业车间调度问题的建模与分析提供有益参考.

关键词:区间作业车间调度; 时间Petri网; 建模与分析

引言

在实际生产过程中,由于系统的实时特性和外界不确定因素的影响,作业操作的持续时间并不能准确地固定下来,但是作业开始和结束的时间范围多数可以界定[1].近年来,国内外研究人员开始探讨基于区间不确定性的作业车间调度问题[2～4],并逐渐成为柔性制造系统调度问题研究的关注点.

区间使用上界和下界刻画时间的不确定性,不仅描述简单,而且容易从实际生产中获取,更便于决策者理解.Lei[1]提出区间作业车间调度问题,并以最小总延迟为优化目标,使用遗传算法求解该问题的优化解.Sotskov[2]等使用区间描述作业加工时间,以最小化加权完工时间为目标,求解单台机器的作业调度问题.Lu[4]等使用区间描述作业加工时间和顺序相关调整时间,以最小化鲁棒调度序列时间与最大完工时间之差为目标,利用局部搜索技术求解单台机器作业调度问题.

近三十年来,Petri网被广泛应用于作业车间调度问题的建模和优化,涌现出许多高水平成果[5～8].但是这些建模方法均采用时延Petri网模型,处理时间约束为确定值的作业车间调度问题,不能有效处理不确定时间约束的作业车间调度问题.因此,研究区间作业车间调度问题的时间Petri网建模与分析方法,对于实际作业车间调度生产具有重要意义.

区间作业车间调度问题是新近提出的作业车间调度问题,现有工作主要集中于问题描述和优化求解方面,在理论模型、动态性质等方面还没有实质性成果,也没有公开发表的文献探讨该问题的Petri网建模和分析方法.时间Petri网是Petri网的时间区间扩展形式[9],很自然可用于区间作业车间调度问题的描述.本文尝试使用时间Petri网作为形式化模型,探讨区间作业车间调度问题的建模与分析方法,为区间作业车间调度问题的研究提供一种有益的探索.

1　时间Petri网

1.1 理论模型

定义1[9]时间Petri网TPN是一个6元组(P,T,Pre ,Post ,M0,SI),其中

(1)P是库所集;

(2)T是变迁集;

(3)Pre: P T →N是前置关联矩阵;

(4)Post: P T →N是后置关联矩阵;

(5)M0: P →N是初始标识;

标识M是一个|P |维向量,M(p)表示库所p的令牌数.

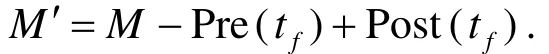
用En(M)表示M的使能变迁集,用Newly(M ,t)表示在M实施t后新使能的变迁集.

1.2 状态类方法

状态类方法是Petri网可达性分析最常用的方法之一.

(1)Mi是标识;

条件(1)保证t使能; 条件(2)保证t不是过期变迁; 条件(3)保证t在与其不冲突的变迁之前实施.用 Fr(Ck)表示Ck的可实施变迁集.

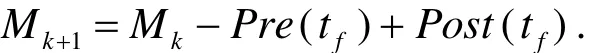
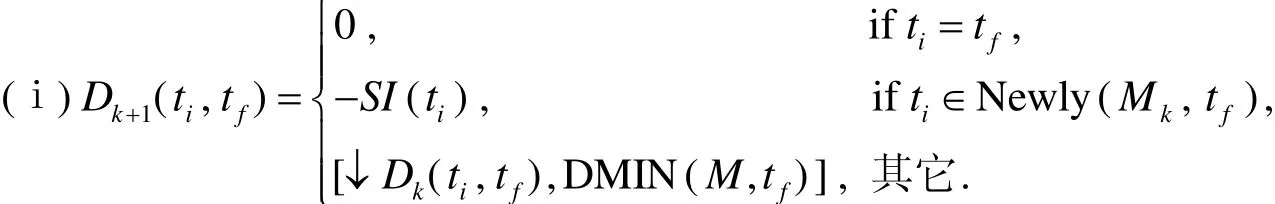
规则(1)计算新标识Mk 1; 规则(2.i)计算tj相对于当前状态类的实施间隔; 规则(2.ii)计算tj和tj之间的相对实施间隔.

2　区间作业车间调度问题建模与分析

2.1 时间Petri网调度模型

作业车间调度问题描述为: 在M个机器上加工N个工件,每个工件Ji由nj个工序组成,工件的每道工序可由多台机器加工.用Oijk表示第i个工件的第j道工序在机器Mk上加工.区间作业车间调度问题采用间隔描述加工时间[1].

考虑一个作业车间调度问题,它由3台机器组成,可处理3种作业,每种作业需3道工序完成.表1描述了每种作业的资源需求.

根据上述需求描述,建立该问题的时间Petri网模型,如图1所示.其库所和变迁说明见表2.

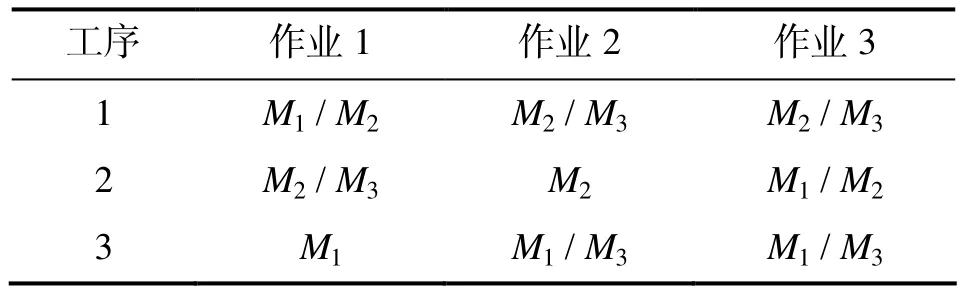
表1 作业的资源需求

图1 作业车间调度问题的时间Petri网模型

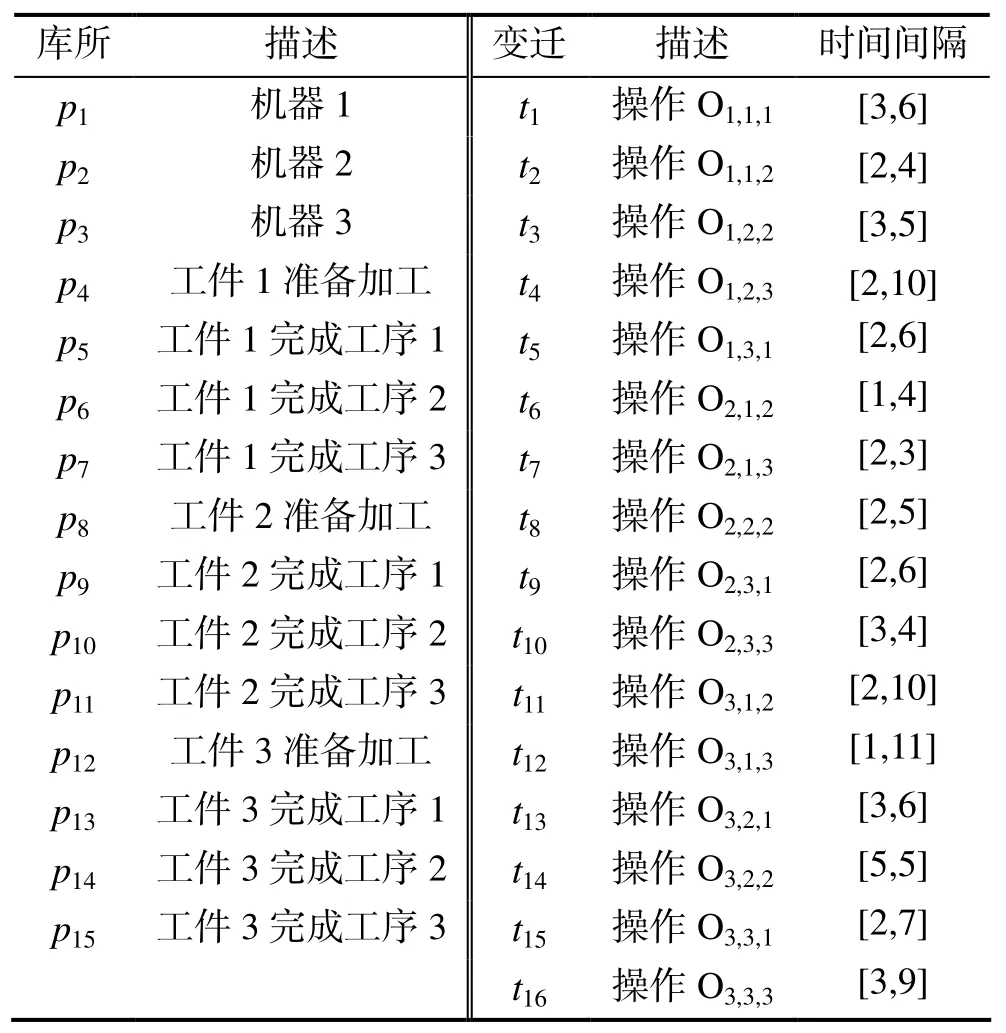
表2 库所变迁描述

2.2 时间Petri网调度分析

作业车间调度就是在满足一定约束条件情况下,在M台机器上安排N个工件的加工任务,并最优化某些性能指标(例如,最小完工时间makespan).

利用第1.2节提出的状态类方法(定义4和定义5),可以构造时间Petri网模型的状态类类树,获得所有可行调度.根据上述状态类方法,研制了基于Matlab平台的时间Petri网建模和分析工具,工具网址为: http://61.187.92.238:8204/html/kexueyanjiu/2013/0614/1053.html.

运用工具对作业车间调度问题的Petri网模型进行状态类分析,共产生状态类244104个,得到可行调度118657条.计算获得最优下界调度为t12t7t2t13t4t8t15t5t10,时间间隔[8,13],如图2所示.计算获得最优上界调度为t12t7t2t4t8t13t5t15t10,时间间隔[9,12],如图3所示.

图2 最优下界调度

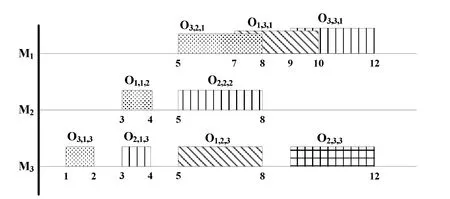
图3 最优上界调度

3　结论

作业车间调度是企业提高生产效率、快速响应市场需求的有效手段.针对新近出现的区间作业车间调度问题,提出基于时间Petri网的形式模型和基于状态类的可达性分析方法,实现了基于Matlab的建模和分析,并运用工具分析了区间作业车间调度问题的优化调度,为区间作业车间调度问题的建模和分析提供了一条新的探索途径.

参考文献

[1] Lei D M.Interval job shop scheduling problems[J].The International Journal of Advanced Manufacturing Technology,2012,60(1-4): 291～301

[2] Sotskov Y N,Lai T C,Werner F.Measures of problem uncertainty for scheduling with interval processing times[J].OR spectrum,2013,35(3): 659～689

[3] Lei D M,Guo X P.An effective neighborhood search for scheduling in dual-resource constrained interval job shop with environmental objective[J].International Journal of Production Economics 2015,159: 296～303

[4] Lu C C,Lin S W,Ying K C.Minimizing worst-case regret of makespan on a single machine with uncertain processing and setup times[J].Applied Soft Computing,2014,23: 144～151

[5] Lee D Y,DiCesare F.Scheduling flexible manufacturing systems using Petri nets and heuristic search[J].IEEE Trans.Robotics and Automation,1994,10(2): 123～132

[6] Li C,Wu W,Feng Y,et al.Scheduling FMS problems with heuristic search function and transition-timed Petri nets[J].Journal of Intelligent Manufacturing,Springer,2015,26: 933～944

[7] Ahmad F,Khan S A.Module-based architecture for a periodic job-shop scheduling problem[J].Computers & Mathematics with Applications,2012,64(1): 1～10

[8] Huang H,Du H,Ahmad F.Job Shop Scheduling with Petri Nets[J].Handbook of Combinatorial Optimization,Springer,2013: 1667～1711

[9] 潘 理,丁志军,郭观七.混合语义时间Petri网模型[J].软件学报,2011,22(6): 1199～1209

Modelling and Analysis of Interval Job Shop Scheduling Problems Based on Time Petri Nets

PAN Li,YANG Bo
(College of Information and Communication Engineering,Hunan Institute of Science and Technology,Yueyang 414006,China)

Abstract:Interval job-shop scheduling problem is a new research hotspot in work-shop scheduling.The existing research work focused on problem description and optimization,but substantial results is lacking on theoretical model and dynamic properties.We present a time Petri net to model interval job-shop scheduling problems,and uses a reachability method based on state classes to analyze all feasible schedules of this model,and then solves optimal schedules with least upper bound and least lower bound.The proposed method can provide a helpful reference for modelling and analyzing interval job-shop scheduling problems.

Key words:interval job shop scheduling,time Petri nets,modelling and analysis

通讯作者:杨 勃(1974−),男,湖南岳阳人,博士,湖南理工学院信息与通信工程学院副教授.主要研究方向: 模式识别

作者简介:潘 理(1975−),男,湖南平江人,博士,湖南理工学院信息与通信工程学院副教授.主要研究方向: 系统建模与优化

基金项目:国家自然科学基金项目(61473118); 湖南省教育厅科学研究重点项目(15A079); 湖南省科技计划项目(2014GK3026)

收稿日期:2015-11-25

中图分类号:TP301

文献标识码:A

文章编号:1672-5298(2016)01-0033-04