柔性多轴向经编聚氨酯涂层织物的拉伸性能

郭囊括， 李丽辉， 代方银， 陈 杨， 敬凌霄,4

(1. 西南大学 纺织服装学院， 重庆 400044； 2. 西南大学 数学与统计学院， 重庆 400715； 3. 重庆大学 航空航天学院， 重庆 400044； 4. 东华大学 纺织学院， 上海 201620)

柔性多轴向经编聚氨酯涂层织物的拉伸性能

郭囊括1， 李丽辉2， 代方银1， 陈 杨3， 敬凌霄1,4

(1. 西南大学 纺织服装学院， 重庆 400044； 2. 西南大学 数学与统计学院， 重庆 400715； 3. 重庆大学 航空航天学院， 重庆 400044； 4. 东华大学 纺织学院， 上海 201620)

为获得多轴向经编聚氨酯涂层织物的各向增强性能，沿涂层织物0°、22.5°、45°、67.5°和90° 5个方向裁取试样，以单轴拉伸试验为基础，分析了织物的拉伸曲线和弹性模量；同时采用数字图像相关系统(DIC)，分析了织物的形变特征，计算了泊松比。利用正交各向异性模型对22.5°和67.5°方向的弹性模量和泊松比进行预测。结果表明：该材料具有良好的延伸性，各个方向试样的延伸度均大于400%；越接近67.5°弹性模量越大；由DIC云图分析得知，拉伸初期该材料的横向收缩变形是不均匀的，中间收缩较快，边缘收缩得较慢，而纵向拉伸变形相对均匀；使用正交各向异性关系对涂层织物的弹性模量和泊松比有较准确的预测，误差的绝对值都小于23.69%。

多轴向经编； 涂层织物； 拉伸性能； 正交各向异性

多轴向经编柔性复合织物是指在增强结构上覆盖一层高分子物或者其他化合物而形成的一种高分子复合材料，具有密度低，强度高，韧性好等特点。铺层的增强纱线可设计性强，且能充分发挥其力学性能，因此该柔性复合材料被广泛应用于航空航天、建筑工程、汽车工业、风力发电的叶片等领域[1-2]。在实际应用中对其力学性能的掌握十分必要。文献[3]通过拉伸试验，探索纱线层面密度，层数及铺层顺序等对织物断裂强力的影响。对比机织增强基布、经编双轴向、经编多轴向的增强基布以及将材料涂层后的拉伸性能发现，多轴向经编织物的性能最优[4-5]。基于合理假设建立了多轴向经编织物的理论模型[6]，结合现代多轴向经编技术进一步深入研究，建立了带有短切毡的单元结构模型[7-8]。文献[9-10]通过拉伸试验发现PVC建筑膜材是典型的正交各项异性材料，通过3次拉伸试验后，发现复合膜材的弹性常数符合正交各项异性关系，且都满足正交各项异性关系[11]。但是以上复合材料的增强织物均为机织物，而对于多轴向经编增强织物拉伸性能的研究相对较少。

本文以单轴拉伸为基础，配合数字图像系统(DIC)[12-13]。对多轴向经编涤纶增强织物的拉伸性能进行深入研究。试验对材料小变形范围内拉伸曲线的特征及重要工程参数的计算作了详细讨论，并使用正交各项异性模型预测该涂层织物偏轴方向的弹性模量和泊松比。

1 试验部分

1.1 试验材料及设备

图1示出柔性多轴向经编织物的结构。增强纱线为涤纶工业长丝，捆绑纱为涤纶工业长丝的拉伸变形丝。增强纱线从4个方向衬入，衬入顺序为经向为90°和-45°方向，纬向0°和45°方向，纱线衬入完成后用捆绑纱固定。基布的宽度为1.27 m，平均厚度为0.138 mm，面密度为217 g/m2。复合材料的制造采用的流延法，将熔融的聚氨酯(PU)颗粒与基布挤压粘合在一起，压合后涂层材料的平均厚度为1.28 mm，平均面密度为1 418.8 g/m2。

单轴拉伸试验使用的是瑞格尔6100万能拉伸试验机，预加张力为5 N，加载速度为100 mm/min，应变率为0.0278/s。试样形变测试使用的是数字图像相关(DIC)系统，图片采集频率为5帧/s。试验在采集图片时使用了2个相机，以便测出试样三维的形变情况。

1.2 试样的准备

试样裁剪以基布的纬向为基准方向，分别沿偏离基准方向的0°、22.5°、45°、67.5°和90°这5个方向裁取试样，每组的有效试样为3个。试样的外形尺寸为200 mm×50 mm，有效拉伸尺寸为中心的100 mm×50 mm。由于DIC系统测试试样泊松比的需要，试验前需要在试样的表面喷涂对比度明显的白底黑点的散斑。图2示出拉伸前喷好散斑的试样实物图。

2 结果与分析

2.1 织物拉伸性能分析

图3示出试样5个方向的拉伸载荷-位移曲线。由曲线可知试样的拉伸位移均大于400 mm，说明试样的延伸率可以达到400%。可以知道拉伸后期试样各个方向的载荷均保持在500 N左右，而此时材料内部的增强纤维已经断裂，说明复合材料内部的增强纤维断裂以后，该柔性复合材料仍然能够承受住一定的拉力，具有较低的危险系数。

2.2 织物模量分析

图4示出试样拉伸前段的应力-应变曲线。可看出45°方向的断裂强力最大，并且明显高于其他角度，初始模量也偏高。这主要是由于45°方向的增强纱线的质量最大。从图中还可看出，67.5°～90°方向初始模量也较大，90°方向的模量高。这是因为该方向的纱线经过整经，纱线排列平直程度高，因此达到相同的伸长率就需要更大的拉力，从而导致模量上升。 67.5°处于45°和90°之间，该方向试样内部斜向纱线多且长，导致拉伸初始阶段存在较大剪切力，从而使该角度的初始模量变大。

从图4的应力-应变曲线还可以看出，除0°方向外，其余角度的曲线在拉伸初始阶段都有1个明显的转折点。图5示出双折射计算泊松比的示意图。为了得到更精确的初始模量，除0°外，都采用双直线拟合，得到模量E1(初始模量)和E2(0到最大应力的80%)。图6示出各角度弹性模量的值。后文验证正交各项异性关系预测时用的是E1。

2.3 织物泊松比分析

图7示出DIC计算的应变云图。图7(a)为DIC重构的试样表面，重构图上的点是确定试样的初始位置的坐标原点，泊松比就是利用这些点坐标位置的改变来计算。图7(b)、(c)是试样整体拉伸1 mm时，X方向和Y方向的应变云图。可以看出，X方向的形变是不均匀的，从蓝色部分得知试样中心区域收缩较快，而边缘的收缩相对较慢。还可以看出Y方向试样的形变相对X方向均匀，但也不完全均匀，因此试验在计算泊松比时选取了DIC重构图上获得的所有横向线段和纵向线段进行计算。

图8示出未拉伸时试样DIC重构的侧视投影图。在拉伸前试样不平直，且由于材料运输及夹具原因不可避免，因此在计算织物实际应变时不仅需要考虑x,y平面位移的变化，还需考虑z方向的位移。故本文计算泊松比的方法为：根据DIC输出试样上全部点的三维坐标位置，计算所有横向线段缩短的平均值和纵向线段伸长的平均值，相除后取绝对值，经拟合得到试样的泊松比，结果见表1。

3 正交各向异性材料模型

正交各向异性材料满足以下方程式[9-10]：

(1)

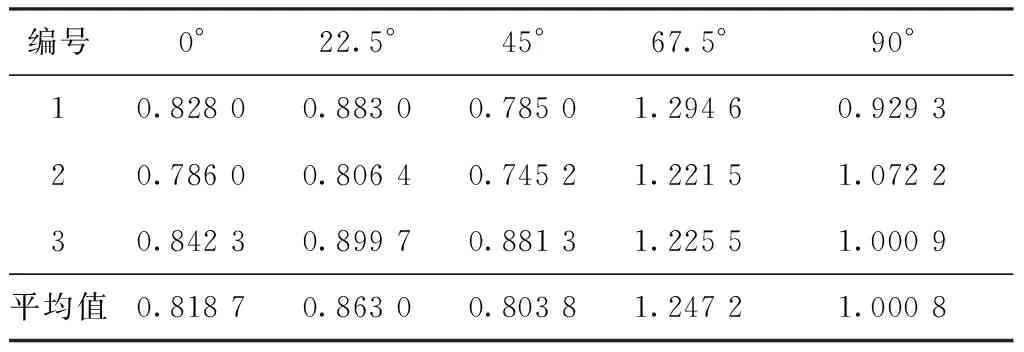
表1 试样的泊松比Tab.1 Poisson′s ratios of specimens

式中：1、2代表材料的主轴方向；x、y分别代表加载的方向；E，ν和G分别代表弹性模量，泊松比和剪切模量。G未知，但是可用45°方向的模量和泊松比代替。让E3=E45°，ν3=ν45°，因此有:

(2)

利用式(2)即可预测出22.5°和67.5°方向的初始模量和泊松比。表2所示为初始模量的预测结果。表3为泊松比的预测结果。

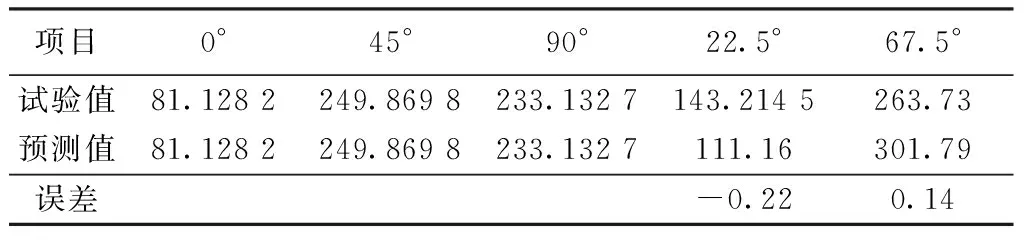
表2 弹性模量的预测结果Tab.2 Predicted results of elastic modulus

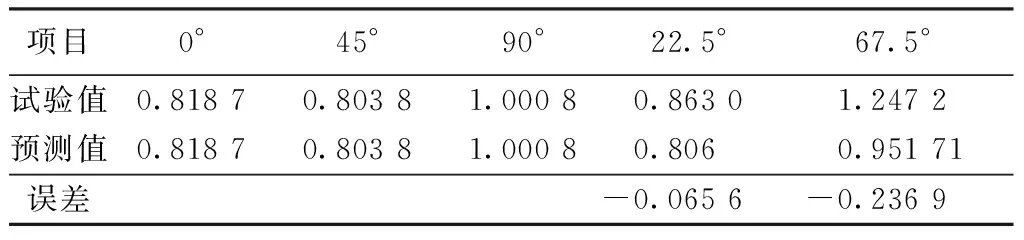
表3 泊松比的预测结果Tab.3 Predicted results of Poisson′s ratios

由表2得出22.5°和67.5°弹性模量预测结果的误差分别为-22.38%和14.43%。由表3得出22.5°和67.5°泊松比预测结果分别为-6.56%和-23.69%。高强工业涤纶丝弹性大，纱线柔软，使得增强纱铺层规整程度低，在拉伸过程中容易受到其他角度纱线及表面膜材的影响，不同试样计算得到的弹性模量的离散程度较大。所以，22.5°和 67.5°方向的弹性模量和泊松比的预测结果误差都小于23.69%。说明正交各向异性模型对材料弹性模量和泊松比有良好预测。

4 结 论

1)由多轴向经编柔性材料的拉伸曲线可知，材料是各向异性的，拉伸强力与材料的方向及该方向的纱线密度有关。

2)由模量可知，67.5°方向的初始模量最大，说明斜向纱线多而长时剪切力对材料初始模量影响较大。

3)通过DIC记录结果得知初始阶段材料的横向变形是不均匀的，中间区域变形快，边缘区域变形慢；但纵向拉伸形变相对横向比较均匀。

4)通过正交各向异性模型预测的22.5°和67.5°方向弹性模量和泊松比的误差绝对值都在23.69%以内，属可接受范围。说明通过单轴拉伸试验得到的柔性多轴向经编织物的弹性常数和泊松比符合正交各向异性关系。

FZXB

[1] 周荣星,陈明珍. 经编多轴向技术及其在复合材料中的应用[J]. 武汉纺织工学院学报,1999(3):81-85,90. ZHOU Rongxing, CHEN Mingzhen. MWK(multi axial-warp-knitting)technology and its application in composite[J].Journal of Wuhan Textile University, 1999(3):81-85,89.

[2] 蒋高明,顾璐英. 多轴向经编技术的现状与发展[J]. 纺织导报,2009(8):53-56. JIANG Gaoming, GU Luying. Status-quo and develop-ment of the multi-axial warp-knitted technology[J]. China Textile Leader, 2009(8):53-56.

[3] 苏丹,缪旭红. 多轴向经编增强材料的拉伸性能[J]. 纺织学报,2011,32(10):61-65. SU Dan, MIAO Xuhong. Tensile properties of reinforced multi-axial warp knitted fabrics[J]. Journal of Textile Research,2011,32(10):61-65.

[4] 陈南梁. 多轴向经编增强复合材料拉伸性能的研究[J]. 东华大学学报(自然科学版),2001(2):99-101. CHEN Nanliang. Tensile properties of multi-axial warp knitted reinforced material [J]. Journal of Donghua University(Natural Science Edition), 2011(2):99-101.

[5] 宁煜,陈南梁. 涤纶多轴向经编织物增强柔性复合材料拉伸性能的研究[J]. 产业用纺织品,2005(8):19-22,30. NING Yu, CHEN Nangliang. Research on the tensile properties of the composite reinforced with multi-axial warp-knitted fabrics of the PET fibers[J].Industrial Textiles,2005(8):19-22,30.

[6] 高金花,李炜. 多轴向经编针织增强材料的几何模型[J]. 东华大学学报(自然科学版),2008(2):149-154. GAO Jinhua, LI Wei. Geometric model of multi axial warp-knitting reinforcement materials[J]. Journal of Donghua Textile University(Natural Science Edition), 2008(2):149-154.

[7] 顾璐英,蒋高明,缪旭红,等. 多轴向经编复合材料预制件的几何模型[J]. 纺织学报,2011,32(11):42- 48. GU Luying, JIANG Gaoming, MIAO Xuhong, et al. Geometric model of multi-axial warp knitted composite perform[J]. Journal of Textile Reasearch,2011,32(11): 42-48.

[8] JIANG G M, GU L Y, CONG H L, et al. Geometric model for multi-axial warp-knitted fabric based on NURBS[J]. Fibres & Textiles in Eastern Europe, 2014, 22(3): 91-97.

[9] 邹宗勇,韩建,刘杭锋，等. PVC建筑膜材拉伸异向性能研究[J]. 浙江理工大学学报,2010(2):186-190. ZOU Zongyong, HAN Jian, LIU Hangfeng, et al. Orthotropic behavior of PVC architectural membrane materials under tensile loading[J].Journal of Zhejiang Sci-Tech University,2010(2):186-190.

[10] CHEN S H, DING X, YI H L. On the anisotropic tensile behaviors of flexible polyvinyl chloride-coated fabrics[J]. Textile Research Journal, 2007, 77(6): 369-374.

[11] 易洪雷,丁辛,陈守辉. PES/PVC膜材料拉伸性能的各向异性及破坏准则[J].复合材料学报,2005(6):98-102. YI Honglei, DING Xin, CHEN Shouhui. Orthotropic behavior and strength criterion of PES/PVC[J].Acta Materiae Compositae Sinica,2005(6):98-102.

[12] PINTO J M T, TOUCHARD F, CASTAGNET S, et al. DIC Strain measurements at the micro-scale in a semi-crystalline polymer[J]. Experimental Mechanics, 2013, 53(8): 1311-1321.

[13] KRAFT S M, MOSLEHY F A, BAI Y, et al. Characterization of the orthotropic elastic constants of a micronic woven wire mesh via digital image correla-tion[J]. Experimental Mechanics, 2014. 54(4): 501-514.

Tensile properties of polyurethane-coated multi-axial warp knitted fabric

GUO Nangkuo1， LI Lihui2, DAI Fangyin1, CHEN Yang3， JING Lingxiao1,4

(1. College of Textiles and Garments， Southwest University, Chongqing 400715, China； 2. College of Mathematics and Statistics, Southwest University, Chongqing 400715, China; 3. College of Aeronautics and Astronautics, Chongqing University, Chongqing 400044, China; 4. College of Textiles, Donghua University, Shanghai 201620, China)

In order to study on the reinforcement properties of PU-coated multi-axial warp knitted fabric, five directions with 0°, 22.5°, 45°, 67.5° and 90° of this material were cut for uniaxial tension experiment. The tensile curves and the elastic modulus were analyzed. The deformation behaviors were observed and Poisson′s ratios were calculated by utilizing the digital image correlation (DIC) system. Lastly, orthotropic model was used to predict the elastic modulus and Poisson′s ratio in 22.5° and 67.5° directions. It is found that this coated fabric has a great elongation with more than 400%in five directions. And the closer to 67.5° is, the greater of the elastic modulus is. At the beginning of tensile, it can be obtained by the DIC system that the transverse shrink deformations are inhomogeneous, it shrinks faster in the center but slower at the edge of the specimens, but the longitudinal tensile deformation is relatively uniform. There is a good prediction of the elastic modulus and Poisson′s ratio by using orthotropic model, and the absolute error value is less than 23.69%.

multi-axial warp knitted; coated fabric; tensile property; orthotropic anisotropy

10.13475/j.fzxb.20150706405

2015-07-28

2016-07-21

中央高校基本科研业务费专项资金资助项目(XDJK2013C132，XDJK2014C127)

郭囊括(1992—)，女，硕士生。主要研究方向为多轴向经编复合材料的力学性能。李丽辉，通信作者，E-mail: llhlx@swo.edu.cn。

TB 332

A