基于WLCS-ALA模型的建设项目投资估算研究
段晓晨, 吕 倩, 张小平, 王玉满
(1. 石家庄铁道大学 经济管理学院,河北 石家庄 050043; 2. 河北地质大学,河北 石家庄 050031)
近年来,我国已进入建设项目投资高峰期,建设项目的投资、建设以及后期的运营,对于我国的经济增长具有直接和间接的推动作用。“十二五”期间,我国市政公用基础设施投资总额达7万亿左右;预计到2020年,全国铁路营业里程将达12万km以上。如此巨大的建设规模和投资,其投资管理的意义和重要性可想而知。目前,建设项目投资管理领域依然还存在着“三边三超”“马拉松”“短命建筑”等现象,造成了对投资的严重浪费。究其主要原因是目前我国建设项目仍然普遍采用传统的定额概预算编制方法进行投资估算,针对已有类似分项通常采用概预算定额和估算指标进行估算,针对无类似分项通常采用比较分析、经验判别等方法进行估算,定额指标本身存在静态性和计划性的特点,导致不能准确有效估算投资额度,估算准确性得不到有效保障[1],并且传统的估算方法采用简单线性估算,不能满足建设项目本身所具有的复杂特性。
全生命周期造价理论,在欧美等发达国家发展已经基本成熟,应用领域广泛,包括环保、能源、军事国防以及建筑领域。具体到国内的发展,2000年,戚安邦[2]提出了应用全生命周期理论对工程项目造价进行管理;丁士昭探讨了建立建设全生命周期工程项目的信息管理系统,从而解决工程项目决策阶段投资额度控制情况等相关问题[3]。
人工生命系统是由Andrew和Norman首先提出,是一个人工生命群落的模型。人工生命理论通过利用达尔文进化论的原理,在计算机中设计与生命类似的实体,并设计一些行为规则算法,来指导进化过程,该过程使生命由简单到复杂、由低级到高级渐进演化,逐步完善自身的适应性,其原理是进化计算在计算机仿真学上的全新应用,进化是生命存在与发展的具体过程。国内学者张军[4]构建了一种基于遗传算法的人工生命的进化模型;谢汝林[5]仿真模拟了他构建的人工生命体的行为选择及其进化模型;高睿等人详细介绍了人工生命算法的基本原理、改进措施、算法应用[6]。
可以发现,全生命周期造价理论和人工生命系统都是相对成熟的理论体系,被国内外学者应用在不同的领域。但二者相结合来进行建设项目投资估算的研究较少。因此,针对建设项目投资建设复杂性特点,采用非线性方法进行投资估算,通过运用建设项目全生命周期造价WLC(whole life cost)和显著性成本CS(Cost-Significant)理论以及人工生命进化理论来构建WLCS-ALA(Whole Life Cost-Significant-Artificial Life Algorithm)模型,进行建设项目投资估算,将人工生命算法应用于投资预测问题,准确拟合已完工程历史数据,以解决其存在的静态性、延时性和滞后性等问题,尽可能达到减少工作量,提高准确性的目的。在保证工期质量的前提下[7],控制政府投资项目的投资额度,为决策管理和实施部门提供决策依据。
1 构建全生命显著性造价人工生命进化模型
1.1 全生命周期造价WLC(Whole Life Cost)
全生命周期造价确定模型采用NPV法,使用以下模型[8]
( 1 )
式中:COm为备选方案m的最初成本;T为项目全生命周期;dOmt为项目运营成本的折现值;dMmt为项目养护成本的折现值;dSAVm为项目期末回收净值的折现值。
式( 1 )可以计算整个工程项目的全生命周期造价,但同时可以预见到计算工作量会非常繁琐巨大。本文将显著性成本理论应用于WLC中,可以简化全生命周期造价计算过程,即[9]
( 2 )
式中:C(csi)mt为项目全生命周期内的显著性成本;d为项目期望折现率;D为项目最终弃置后的净值;csf为项目的显著性因子;n为显著性项目的个数;NPVm为项目全生命周期造价的现值之和[10]。
1.2 人工生命进化算法ALA(Artificial Life Algorithm)
人工生命进化算法是通过研究生物个体进化自然选择规律,对工程技术领域或其他领域进行优化计算、预测和数字寻优的一种数学模型。其本身具有自组织、自学习、自进化等优点,在全局范围内具有良好的收敛性能和鲁棒性[8-11]。

X={x∈Rn|xmin≤x≤xmax}
( 3 )
每个生命体Xs有邻域C,Xs的邻域C是一种欧几里德空间,可描述为
C={x∈Rn|‖x-xs‖2≤D}
( 4 )
式中:xs表示人工生命体当前的位置;D为人工生命体的活动区域,人工生命体在这个区域内移动、繁殖。每个坐标点都分布着食物能量源和一定数量的人工生命体。在每次演化中,它们可以在这个区域内发现资源和其它人工生命体。通常把D作为一个常数用于循环过程,有时也定义为一个变量随着循环次数增加而变化。
在前期迭代中,人工生命体搜索的邻域范围广阔,它们有更多的机会找到优化解。随着迭代进行,它们将搜索优化解的区域范围由初始的广阔区域转为一些较小的优化解区域,因此可以做到全范围优化解。
把人工生命体生存的环境视为目标优化问题的求解空间,在这个求解空间中的人工生命体可以进行交互活动。对人工生命体的生存繁衍规则进行定义,该定义使其具有搜索特性,可以求解目标优化问题的极值,在求解空间中与优化函数极值区域形成有效突现聚类。
1.3 全生命显著性造价人工生命进化模型优化过程[13-15]
Step1初始化:初始混合编码,产生POPSIZE个人工生命体,并将其随机性的分布在人工系统中。定义每个人工生命体初始能量为IE。
Step2搜索资源:每个人工生命体在人工系统REGION内寻找可以进行代谢的资源。
Step3移动:如果人工系统内具有距离人工生命体很近并且为人工生命体所需要的资源,那么人工生命体就向该资源移动;否则人工生命体会在邻域内进行随机移动。
Step4代谢:人工生命体向符合条件的资源移动,通过进食和代谢,最终增加能量值WE。
Step5增加年龄:通过初始化、搜索资源、移动和代谢,人工生命体的年龄加一。
Step6繁殖下一代:最后当人工生命体年龄达到生育年龄RA和获得一定的能量值后,就符合繁衍条件,在人工系统内与相同种类的人工生命体进行繁殖活动,后代会继承父代的基因和知识等遗传信息。
Step7减少能量:在这一过程中,系统内的全部人工生命体都会降低内在能量,当人工生命体的内在能量值低于最低的能量阈值MSE时,那么这个人工生命体就会灭亡,最终会从环境中消亡[16]。
Step8增加代:在这一过程中增加一代,返回步骤Step2。参数说明见表1。

表1 参数说明
2 研究案例
本文收集大量相关的已完公路工程历史数据作为基础数据,并利用净现值法求各工程的WLC(折现率设定为5%),在进行数据分析前,需要消除时间差距和地区差距,进行降噪处理,利用造价指数进行时间和地区调整,将数据都转化为基期为1995年、基准地为北京地区的统一数据。
2.1 确定拟建工程特征量化值
参考相关资料,根据专家经验并分析高速公路项目中路基项目的特点以及施工工艺特征,总结出路基的工程特征类目[17],高速公路路基工程的特征量化描述见表2。
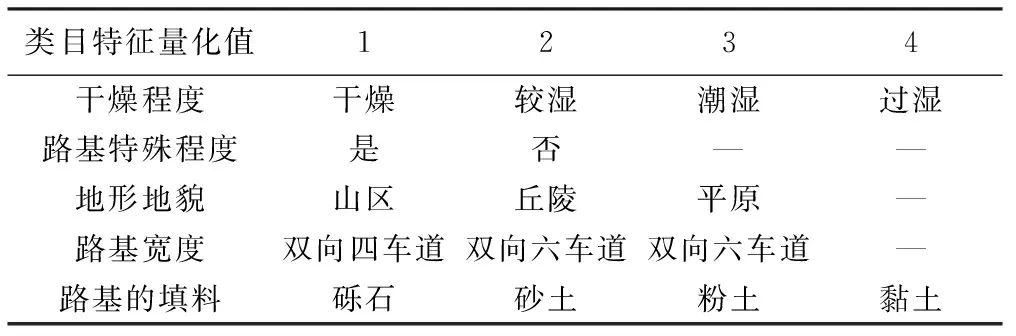
表2 高速公路路基工程的特征量化描述
所选取的拟建工程的路基分部工程特征量化值为(2,1,2,1,3),以此为筛选条件,在历史数据中寻找具有此类特征的路基工程,即为需要的类似工程。在此找到了10项类似工程。
2.2 CS理论数据挖掘
全生命周期造价包括初始的建造成本和未来的运营及维护成本,所寻找的全生命显著性成本项目就是在建设成本和运营维护成本中寻找。初始建设成本采用工程量清单中的成本,运营维护成本采用公路管理处所提供的维护数据,即在工程量清单和运营维护数据中寻找显著性项目。
2.3 利用CS理论处理数据
(1) 以已寻找到的10项类似工程为研究对象,分别计算得出路基分部的各分项工程的全生命成本,利用均值理论找出显著性项目CSIs。
(2) 消除数据的时间差异和地区差异,通过式( 1 )计算整个工程的全生命周期造价。
(3) 计算显著性因子,根据式( 2 )csf由每个CSIs的造价CCSIs除以全生命周期造价得出。
通过以上的数据处理步骤进行处理后得出类似工程的路基全生命周期的显著性项目见表3,显著性造价、显著性因子、全生命周期造价表示见表4。

表3 路基全生命周期造价的CSIs

表4 样本数据表 万元/m
根据表3,可以看出在工程造价中存在着显著现象,显著性项目的数量占总数量的20%左右,而显著性项目的总造价确是全生命周期造价的80%左右,符合显著性理论。并可知同类工程具有比较相似的显著性项目和比较一致的显著性因子。
2.4 ALA-WLC投资预测模型设计
本文采用matlab语言形式设计一个人工生命模型[18-20],该模型符合人工生命体模式,构建的优化函数即为人工生命体的适应度函数[21]。用Artificial Life1.4.0小程序软件进行JAVA模拟演示,数据的仿真通过Matlab语言实现。
表4中LJ1~LJ9为测试样本,LJ10为预测样本。通过求出类似工程的历史显著性造价的均值和显著性因子均值,确定寻优数据空间作为人工生命进化模型优化的数据基础[22-23]。
Step1采用混合实数编码方式对人工生命体进行编码。
(1) 定义随机数据β,
β∈{0,0.01,0.02,…,0.1,0.11,0.12,…,0.2,…,1}。
(2) 计算xi=li+β(ui-li),重复N次(N为变量的个数)后,则产生一个人工生命体x={x1,x2,…,xN}。其中,N=2,x1为显著性成本项目造价,x2为显著性因子数值。
(3) 重复(1)、(2)M次(M为种群大小),则会产生一个包含M个人工生命体的初始化种群。
确定变量的求解空间,初始值是通过对同类工程的显著性项目造价和显著性因子求平均值得出的。li和ui由变量的初始值乘以0.8和1.2得出。
Step2适应度计算。
基于ALA算法的造价投资预测,实际上就是基于以往已知的类似工程造价基础上寻找更加准确的造价预测值,所以与实际值的误差越小,其适应度越高。本文以适应度越高越好来衡量个体的优劣。
算法描述如下

( 5 )
式中:Z为待寻优的变量x1和x2;E(Z)为目标函数;L、U为可行的解空间;x1为显著性项目造价;x2为显著性因子;O为目标值即实际造价。
Step3参数设置。
经试验测试,合理的参数设置见表5。

表5 参数设置
注:种群规模越大,算法耗费的时间越多。因此参数POPSIZE要求选取合理范围,才能确保增强算法收敛性能和运行的速度。REGION的设置必须考虑寻优区域的大小,将MAX定义为优化过程最高限额,将MIN定义为优化过程最低限额,通过一系列的实验过程,定义优化问题的维数N,则人工生命体的活动区域为N*(MAX-MIN)/10,在此区域内进行寻优就会取得比较好的效果。GENERATION对算法的影响是:50代到200代之间,随着世代增加,算法的寻优精度提高,但是,当算法运行到400代时,就会出现过拟合现象,算法寻优精度开始降低。根据经验总结,这种过度拟合现象一般发生在200代以上,因此设置迭代次数参数应在200代以内。
Step4根据构建的人工生命进化模型优化过程,进行结果分析。
(1) 迭代循环过程。图1中为人工生命系统经过200代循环后得到的分布图。

在算法的初始阶段,人工生命体在人工生命世界中随机分布,然后它们开始互相交流、学习,进行搜索行为;经过100代迭代后,优化解区域初步形成,多数人工生命体聚集在优化解区域;经过200代后,如图1示,人工生命体基本在优化解区域形成突现聚类,收敛于优化解。在此基础上,比较每个生命体的适应值,就可以得出最优解。
表6和图2显示了人工生命进化过程中系统逐步趋于稳定,各个个体都进化到较优状态,具有很好的收敛性能,在运行200代后突现,有效地达到优化结果。
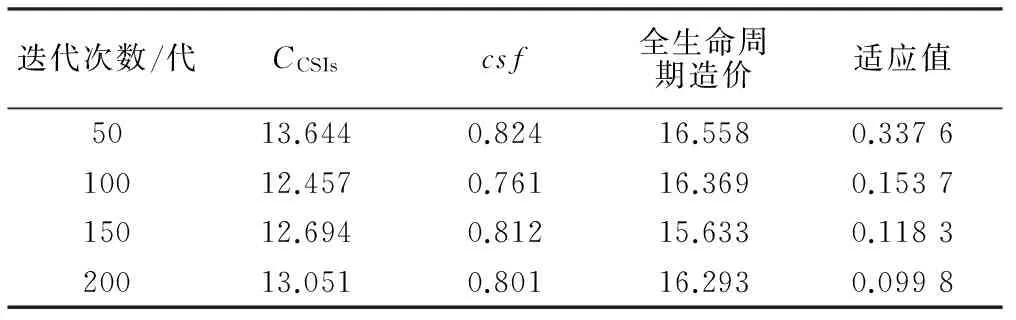
表6 各代最优个体的适应值变化
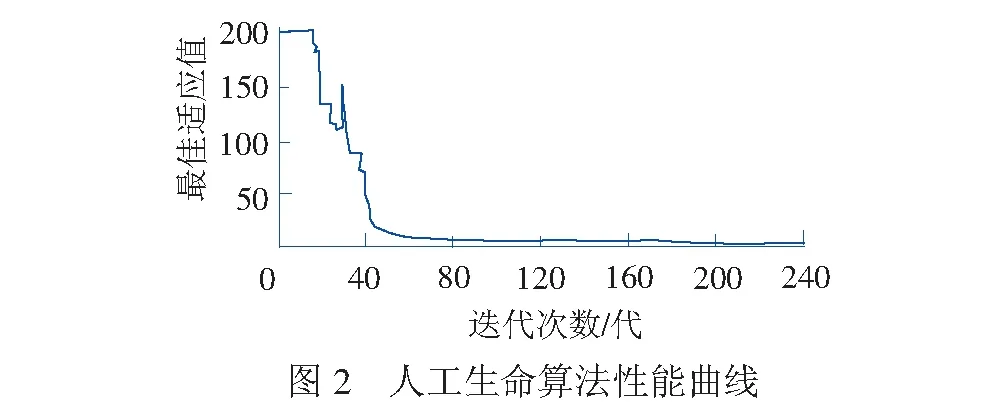
(2) 优化结果分析。
人工生命体在进化200代之后可以发现达到了较好的收敛效果,从而可以寻找出其最优生命个体,最优解见表7,Best这一行即为最优解,由此确定项目单位每米造价预测值为16.293万元。人工生命体与CS投资估算方法对比分析见表8,可以发现人工生命体预测误差在10%以内,表明这一投资预测有效可行。
用人工生命进化模型分别对显著性造价CCSIs和csf进行预测,表8对人工生命进化方法预测与CS方法预测的结果进行对比,可分析出:人工生命预测的全生命周期单位造价精确度远高于传统CS方法精确度,说明在投资决策领域应用人工生命进化方法会使投资预测更加精确。

表7 200代优化结果

表8 人工生命与CS投资估算方法对比分析
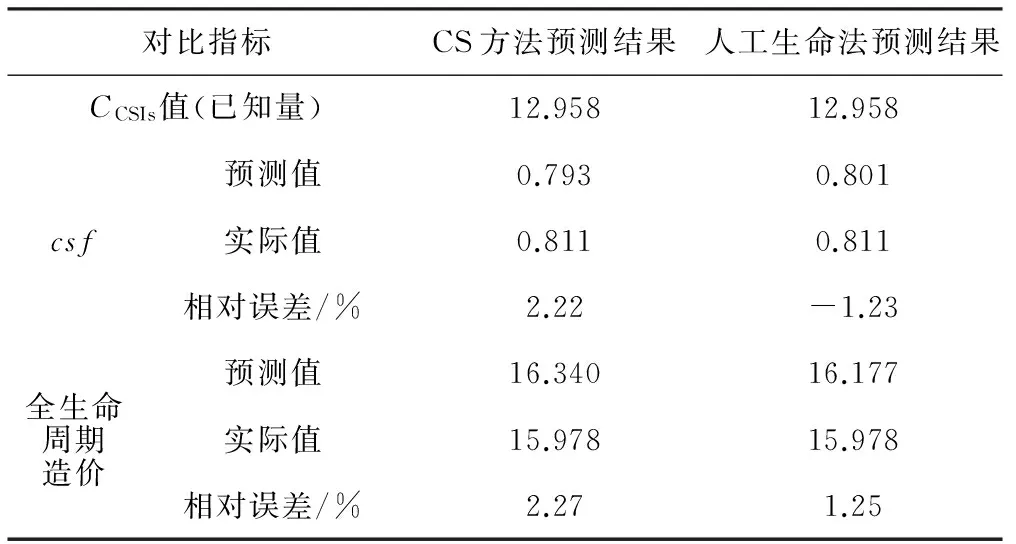
表9 设计阶段人工生命与CS方法预测对比分析
此预测模型也可用于施工图设计阶段的施工图预算,如表9即为进行施工图预算的结果,即用人工生命方法预测出csf,再根据同类工程确定拟建工程有哪些显著性CSI项目,根据拟建工程施工图纸据实算出CSI项目的造价,为12.958万元/m造价,再除以预测的csf,得出全生命周期造价。将结果与CS方法平均计算的csf的结果准确度比较,说明两种方法均达到要求误差3%。但人工生命方法比CS方法准确性提高。
3 结论
结合全生命显著性造价理论和人工生命进化算法理论,建立WLCS-ALA模型,本文构建的非线性投资估算预测模型,探讨人工生命进化算法在工程造价领域的应用。运用实际收集的工程数据验证了模型准确度,从而进行了实证分析。人工生命进化算法能够有效解决以前造价线性预测、均值预测、预测准确度低的问题,较好的拟合工程造价的非线性特性,因此具有较好的收敛性能,能在全局范围内搜索得出最优解,预测误差较小,因此造价预测具有较好的可行性和有效性。同时全生命显著性造价可以大大降低计算的工作量,提高工作效率,简化数据处理量。
工程造价受时间因素影响较大,具有动态性和不确定性。从建设项目的全生命周期角度,工程造价经历从最初的不确定到最终确定的过程,但前期不确定性阶段的投资控制对整个项目的投资预测起到了决定性和关键性作用。该阶段是投资估算信息最不充分和最模糊的阶段,其投资估算额是随后各个阶段投资控制的最高目标,它的准确与否对整个项目的各阶段投资控制起着决定性作用。通过CS理论有效挖掘基础数据并进行相关处理,从而为人工生命进化模型提供基础数据,通过非线性的方法更精确地进行造价预测。
同时,由于人工生命进化算法在国内发展还不太成熟,仍存在许多问题有待后续工作的进一步完善和发展。主要表现在:模型构建需进一步探讨更合适的编码方法和适应度函数;模型构建后需要进行编程运行求解,适合于模型运算的软件应进一步开发研究。
参考文献:
[1] 中华人民共和国国家统计局.中国统计年鉴[M].北京:中国统计出版社,2008.
[2] 戚安邦.工程项目全面造价管理[M].天津:南开大学出版社,2000.
[3] 丁士昭.工程项目管理[M].北京:中国建筑工业出版社,2006.
[4] 张军,郑浩然,王熙法.具有行为强化学习能力的人工生命进化模型设计[J].计算机工程,2000,26(10):11-13,50.
ZHANG Jun,ZHENG Haoran,WANG Xifa. Study of the Behavior Reinforcement Learning in Artificial Life Evolutionary Models[J]. Computer Engineering,2000,26(10):11-13,50.
[5] 谢汝林.人工生命体行为选择及其进化研究[M].重庆:重庆大学,2002.
[6] 高睿,周永华.人工生命算法综述[J].控制工程,2005,12(S2):153-156.
GAO Rui,ZHOU Yonghua. Overview of Artificial Life Algorithm[J]. Control Engineering of China,2005,12(S2):153-156.
[7] 段晓晨,张晋武,李利军,等.政府投资项目全面投资控制理论和方法研究[M].北京:科学出版社,2007.
[8] 董士波.全过程工程造价管理与全生命周期工程造价管理之比较[J].经济师,2003(12):136-138.
DONG Shibo. The Comparison of the Whole Life Cycle of the Whole Process of Project Cost Management and Engineering Cost Management[J]. Economist,2003(12):136-138.
[9] 段晓晨,郭兰英,张新宁.新建高铁工程非线性造价估算方法研究[J].铁道学报,2013,35(10):114-122.
DUAN Xiaochen,GUO Lanying,ZHANG Xinning. Research on Nonlinear Estimating Methods of Whole Life-cycle Cost for China High-speed Railway Project[J]. Journal of the China Railway Society,2013,35(10):114-122.
[10] 段晓晨.政府投资项目全面投资控制理论和方法研究[D].天津:天津大学,2006.
[11] LUO Lin,ESTER Van Der Voet,GJALT Huppes. Life Cycle Assessment and Life Cycle Costing of Bioethanol from Sugarcane in Brazil[J]. Renewable and Sustainable Energy Reviews,2009,13(6):1 613-1 619.
[12] GU-TAEK KIM,KYOON-TAIKIM,DU-HEON LEE,et al. Development of a Life Cycles Cost Estimate System for Structures of Light Rail Transit Infrastructure[J]. Automation in Construction,2010,19(3):308-325.
[13] HARIKRISHNA Narasimhan, CHEW M Y L. Integration of Durability with Structural Design:An Optional Life Cycle Cost Based Design Procedure for Reinforced Concrete structures[J]. Construction and Building Materials,2009,23(2):918-929.
[14] JAMIE E Padgett,KRISTINA Dennemann,JAYADIPTA Ghosh. Risk-based Seismic Life-cycle Cost-benefit(LCC-B) Analysis for Bridge Retrofit Assessment[J]. Stuectural Safety, 2010,32(3):165-173.
[15] 王玉满,张宇佳.全面显著性造价投资预测模型研究[J].硅谷,2011,4(2):92.
WANG Yuman,ZHANG Yujia. Research of the Whole Significant Investment Cost Prediction Model[J]. Silicon Valley,2011,4(2):92.
[16] 白冰.基于全生命周期理论的工程造价粗糙集估算方法研究[M].北京:中国地质大学,2010.
[17] 王安麟,马立新,赵群飞.复杂系统的分析与建模[M].上海:上海交通大学出版社,2004.
[18] 洪毅.进化算法中多种信息的利用[D].上海:上海交通大学,2008.
[19] 张仲明,郭东伟,曲明,等.使用人工生命模型解决时变优化问题[J].吉林大学学报(信息科学版),2004,22(5):485-488.
ZHANG Zhongming,GUO Dongwei,QU MING,et al. Solving Time-varying Optimization Problem using Artificial Life Model[J]. Journal of Jilin University: Information Science Edition,2004,22(5):485-488.
[20] 王亚钊.基于捕食策略的人工生命算法及在系统辨识中应用[M].南宁:广西大学,2007.
[21] 阎平凡,张长水.人工神经网络与模拟进化计算[M].北京:清华大学出版社,2005.
[22] 薛定宇,陈阳泉.高等应用数学问题的MATLAB求解[M].北京:清华大学出版社,2005.
[23] 张江,李学伟.用数字人工生命模型探索复杂适应系统[J].复杂系统与复杂性科学,2005,2(1):39-48.
ZHANG Jiang,LI Xuewei. Using Digital Artificial Life to Investigate Complex Adaptive System[J]. Complex Systems and Complexity Science,2005,2(1):39-48.

