政府投资建设项目群资源规划模型研究

乌云娜　肖鑫利　宋宗耘　远建平

摘要：在对政府投资项目群（GIPG）理论及实践研究的基础上，提出以资源利用率最大化为目标的资源规划模型，并引入改进萤火虫算法（Improved Firefly Algorithm）对模型求解。GIPG资源规划过程重点考虑项目管理者、专家群体及社会公众三方面，从而避免负面社会影响，提升公众满意度。最后通过工程算例进行模拟仿真，验证模型及方法的合理性。

关键词：GIPG；资源规划模型；改进萤火虫算法

DOI：10.13956/j.ss.1001-8409.2016.05.09

中图分类号：F205；F224.5 文献标识码：A 文章编号：1001-8409（2016）05-0040-05

Abstract：Based on the theories and practice of GIPG， this paper set up the resource programming model whose target was to maximize resource utilization， and introduced the IFA to solve the proposed model. When the resource of GIPG is programmed， the managers of project group， expert groups and the public were considered， in order to avoid negative social impact and then improve the public satisfaction. In the end， it carried out the simulation analysis of an engineering example to verify the rationality of the proposed model.

Key words：GIPG（government investment project group）； resource programming model； IFA（improved firefly algorithm）

1 引言

政府投资建设项目（GIP）在政府投资中占有重要比重，且具有很重要的社会作用。GIP是指为适应和推动国民经济或区域经济发展，满足社会公众需求，独资或合资兴建的固定资产投资建设项目，借此实现社会利益的最大化。出于对资金来源、社会影响等各方面的考虑，GIP受到社会各界的广泛关注[1]，且审核和建设过程均更加严格。因此，GIP资源规划及使用的合理性不仅受到项目管理者的关注，还是响应国家政策的体现。随着GIP规模和数量的不断扩大，对其实行项目群管理已经成为未来一种趋势。项目群就是一组具有相同战略目标，且需要统一分配资源的多个相互关联项目组成的集合，项目群管理就是针对这样一组项目进行统一的协调、管理，并最终获得单个项目无法获得的效益。项目群内各项目具有自身目标，但都是为项目群战略目标服务[2]。项目群资源规划过程需紧紧围绕战略目标，同时还需重点关注项目之间资源共享及冲突问题。GIPG资源优化规划问题，是在保证资源约束和优先关系的前提下，优化项目各项任务进度安排，从而实现项目群资源的充分利用。

基于相关理论分析，并参考我国社会现状，可知GIPG更加贴近实现经济发展与满足社会公众需求的目标，因此考核此类项目，应该主要从社会需求满足及公众满意角度出发，资源规划问题同样需关注这两个考核标准。目前的项目资源优化模式包括：资源有限、工期最短；工期固定、资源均衡。然而，实际建设项目中，还可能存在此类情形：既要保证项目工期、成本、质量，还需重点关注项目资源的充分利用。具体讲，政府投资项目由于资金来源的特殊性，需要在保证成本、质量、工期的前提下，实现资源的充分利用，避免资源浪费造成的不良社会影响。同时，项目群资源的合理、高效配置对工期产生重要影响，项目群内受限资源的合理配置是保证项目群工期的基础和前提[3]。多项目资源规划仅关注项目资源量和进度的安排，通常不考虑战略目标的影响，尚缺少从项目群角度对资源进行优化规划。虽然形式、解决办法与项目群资源规划问题相似，但两者最主要的差别体现在项目群战略目标是否与目标函数或约束条件产生联系。

基于以上分析，本文从资源利用角度研究GIPG的资源规划问题。由于公众更加关注政府投资效率，而资源的合理配置能从一定程度上体现GIP的投资效率，且资源合理配置更容易被公众直观体会。因此，本文通过合理安排项目工作，降低资源需求与供给能力之间的偏差，以实现项目群资源的持续、稳定供应，防止由于资源短缺导致的窝工及施工计划变更，从而提高政府投资效率，最终提升公众的满意度。具体来讲，本文以资源利用率最高为战略目标，即供给能力和需求之间的偏差最小，保证资源规划的合理、高效。同时，IFA在寻求全局最优方面的优势已在文献[4]中得到验证，因此本文选取改进萤火虫的算法对GIPG资源规划模型进行求解。

2 GIPG资源规划现状分析

目前项目群管理思想已经应用到大型建设项目、基础设施建设等领域[5，6]，但在政府投资领域应用还很少见。目前，针对资源受限多项目资源规划问题的研究，主要从多目标规划及群智能优化模型方法出发。关注点主要集中在多项目管理、多目标优化、资源均衡等方面[7～9]；针对项目资源规划优化方法及模型方面，文献[10]从项目之间资源的相互影响出发，引入微粒群算法，寻求最优的资源规划和整体项目效益；文献[11]结合层次分析方法与动态规划理论，提出了项目群资源管理的改进动态规划算法程序步骤。除此之外，还有学者将遗传算法、蜂群算法等方法应用到项目资源规划问题[12，13]。但是，尚未有研究针对GIPG资源规划问题构建具体模型及求解。

基于以上分析，本文对GIPG构建资源规划模型，并提出基于IFA的优化方法。萤火虫算法是2007年提出的仿生群智能算法[14]，且通过与莱维飞行算法结合后，与标准萤火虫算法、粒子群算法相比具有更强的全局搜索能力[4]。同时，萤火虫算法在解决非线性、复杂约束的多目标优化问题中被验证具有很大的优势[15，16]。除此之外，文献[17]、[18]分别对萤火虫算法在最优解搜索能力、精确性等方面进行验证。同时，萤火虫算法应用领域也在不断拓宽，如风电微观选址[19]、多地区电力系统自动化控制[20]等。研究证明，萤火虫算法在解决多目标规划、非线性规划中的持续、离散优化问题具有很大的优势。将其引入到GIPG资源规划问题中，具有一定借鉴意义。

3 资源规划模型构建

GIPG资源规划是在逻辑与资源约束下，对共享资源和任务进度进行合理分配和调整，从而实现资源的充分利用，最终提升社会满意度。本文立足GIPG自身特点，构建相对应的资源规划模型，即在保证质量、投资等目标的前提下，将战略目标设定为资源的充分利用，并将战略目标具体化为项目群共享资源的利用率最大化，即最小化资源供给能力与资源需求之间的方差。

3.1 资源规划流程

GIPG资源规划过程主要由两阶段构成。第一阶段首先由项目群管理者（Project Group Manager，PGM）邀请具有相关专业背景的专家构成专家组，负责信息处理及算法分析。此阶段，专家组收集国家、地区政策中有价值的信息，以及当地公众对拟建项目的意见，并用定性或定量方法，对收集到的信息进行筛选并提炼出较重要的目标信息，供PGM确定战略目标及项目目标。之后，专家组对PGM确定的各级目标进行合理性验证，对不合理目标提出相应的参考意见，供PGM进一步修正，直到各层级目标均能够验证合理，然后还需要将结果反馈给当地公众，以公众反馈意见为辅助进行目标的调整，此过程能够防止由于各方理解偏差导致的最终目标与初始政策、社会公众意见之间偏差过大。

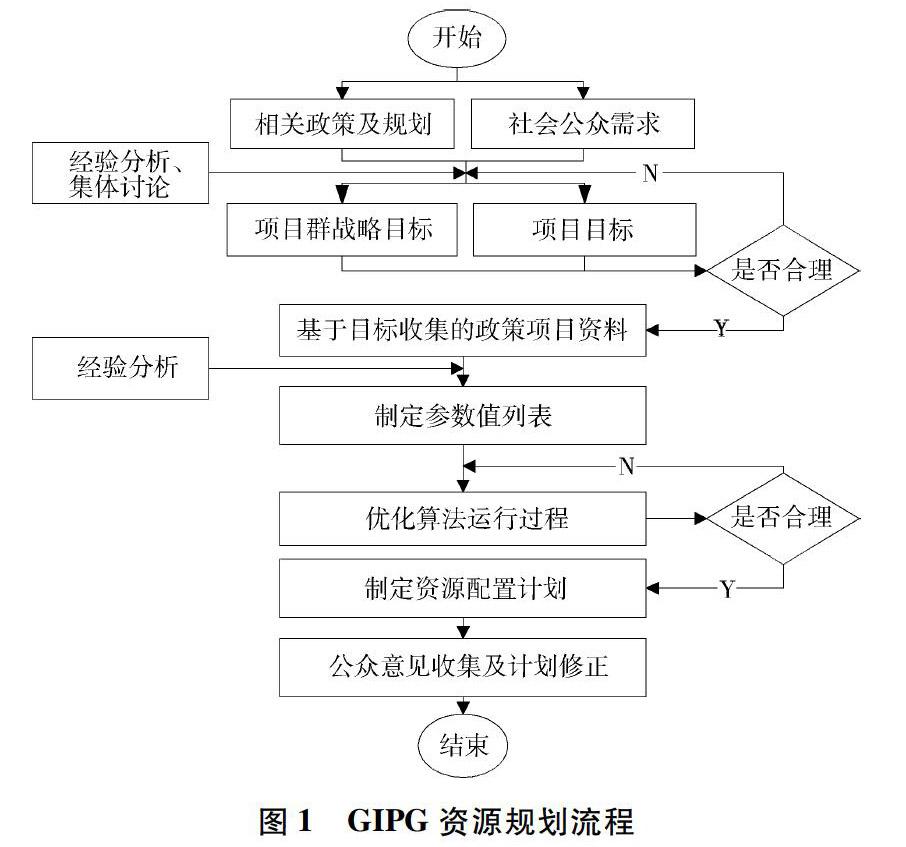
第二阶段为优化算法运行过程，包含从确定目标后项目信息收集、算法参数确定、算法运行、结果分析到方案制定等步骤。PGM根据各级目标收集相关政策及项目数据，以供专家组整理和分析，从而确定算法中各参数值，并通过算法对资源规划模型求解。之后，专家组需要对运行结果进行专业分析并配以一定的解释，以便于PGM依此制定资源配置计划。然后，还需将项目资源计划情况反馈给当地公众，并以公众反馈信息为辅助对结果进行适度调整。图1表示资源规划主要流程。

3.2 资源规划模型

在对项目资源规划进行研究时，确定的总资源能力、指定的截止日期和项目优先关系需要优先考虑[9]。具体讲，项目群资源规划主要受两方面约束：①多种优先关系，本文中仅考虑一种优先关系，即一项任务结束后其紧后工作才能开始；②共享资源可用量有限，但当一项任务被分配一定量资源时该项资源能够稳定供应[21]。除此之外，GIPG存在以下假设：①研究对象为项目群共享资源；②项目间资源配置不考虑地理限制；③资源数量限制内，资源能够稳定供给；④总的资源供给能力为给定值；⑤所有任务能够立即开始且能在规定时间内完成[22]；⑥质量、安全等方面均符合合同要求；⑦各项资源独立供给。

GIPG资源规划研究主要基于以上假设展开。通常，一个项目群包含几个战略目标，但考虑到GIPG自身特点，本文将战略目标设定为共享资源利用率最大化。GIPG由n个项目构成，各包含m项任务，具体数学表达如表1所示。

其中，目标函数求解资源供给与需求之间的资源方差最小值；式（2）和式（3）分别计算第t阶段需求资源总量并限制不超过该阶段资源供给能力；式（4）保证所有任务一旦开始将持续至完成，中间不间断；式（5）反映相同项目中任务的优先关系；式（6）保证所有项目完成时间不超过项目群总计划工期；式（7）和式（8）分别说明变量xijt，Rt，vij的范围。

4 改进萤火虫算法

群智能算法在处理GIPG资源规划这类具有高维、多峰等特点的问题时，容易出现过早收敛、优化精度不足等缺陷，萤火虫算法也不例外。因此，本文选取IFA对资源规划模型进行求解。

萤火虫通过发光特性在搜索范围内寻找伙伴，并向邻域内位置较优的萤火虫移动，从而实现位置优化。萤火虫算法存在三个假设条件：①所有萤火虫无性别差异；②萤火虫间吸引度与光强度成正比，且与距离成反比，如果萤火虫间亮度相同或邻域内无更亮的萤火虫，则随机移动；③光强度与待优化目标函数密切相关。

因此，萤火虫算法主要包含两个要素：光强度和吸引度。亮度大小体现出位置优劣且决定移动方向，吸引度决定萤火虫移动距离。萤火虫间的相对亮度、吸引度均与距离成反比。通过不断更新亮度和吸引度，实现目标优化。IFA的数学描述与分析如下[4]。

定义1：相对亮度公式为：

5 算例分析

为提高居民生活质量，H省计划在Q地同时建设多个保障性居民住宅楼，通过招投标后，Z建设公司担任项目总承包商。Z公司隶属于某中央企业，因此其公司战略需紧跟国家的政策变动。Z公司管理者对住宅楼项目采用项目群管理模式，对各项目进行管理并制定资源配置计划，从而实现项目群资源、进度的统一安排和管理。PGM主要由政策工作部、办公室、项目部、财务部、安全监察部、计划物资部及人力资源部等各部门1名部门领导和1名部门员工组成项目群管理办公室，同时指定1名办公室主任，直接管理各项目负责人。

首先，项目群管理办公室负责构建专家组，专家主要的研究背景包括工程、政府政策、社会学以及计算科学。专家组首先收集国家、地区政策及规划资料，如“十二五规划”。然后通过问卷调查，征求当地公众需求，问卷主要包括个人收入及现住房情况、对保障性住房态度及期望、对国家和地方政策了解程度、对拟建项目意见等内容；问卷发放对象为利益相关公众，具体为22～60周岁人群；问卷发放形式为抽样调查。通过对以上信息分析列出主要的战略目标，并将其呈递给PGM。基于此，PGM经讨论和表决确定战略目标为“提高资源利用率，建设资源节约型企业”。然后，将战略目标具体化为“资源供给和需求间方差小于0.5”，作为各项目管理目标之一，并将混凝土确定为项目群共享资源[23]。然后专家组对各层目标进行合理性验证，主要采取归纳分析和比较分析的方法，结果表明各层目标基本符合政策、公众的要求，且在项目成本、质量等方面均符合要求。

然后，PGM根据各目标，通过咨询项目负责人及实地考察，得到各项目的详细资料，以便于专家组确定优化算法中各项参数。经研究，IFA各参数值确定为：γ=1.0、β0=1.0、α=0.2。

本文借鉴文献[4]中的IFA与遗传算法和粒子群算法对比结果，分别用这三种算法对GIPG资源规划模型进行求解。本文中各算法运行环境相同：Matlab2012版软件；酷睿i3处理器；4G内存。寻优过程及结果如图2至图5所示。图中等目标函数值形成的闭合曲线为等高线，

等高线之间的等高线平距愈小，等高线排列越密，说明目标函数值变化愈快。

由图可知：PSO能够找到各最优值，但容易陷入局部最优解，且最终结果相对较差；GA更多集中在全局最优值处，但部分结果超出范围，存在偶然误差；IFA能够遍历全部极值点，且最终集中在全局最优值处，因此最终结果更优，即IFA具有更强的全局寻优能力。同时根据图5可知：PSO前期收敛速度较快，但后期较慢，且结果超出既定范围，因此被舍弃；GA能以较快的速度向最优值处收敛；由于更新寻优机制，IFA前期收敛速度较慢，但能够遍历全部极值且未陷入局部极值，最终收敛到全局最优值处。

基于以上结果，专家组对其进行合理性验证，确定结果是否符合预期设定的约束条件以及项目实际情况，如有问题继续进行修正直至运行结果符合要求。然后将结果呈递至PGM，经PGM进行可行性验证后，确定最终的资源配置方案。PGM根据专家组意见，最终选取IFA最优值对应的方案为最优资源配置方案。基于已得结果，PGM将资源规划及使用情况反馈给填写问卷调查的公众并征求意见，以公众反馈意见作为辅助条件对结果进行修正，得到最终的项目群资源规划结果，如图6所示。

6 结论

由于GIPG重要的社会地位以及资源规划在GIPG协调和管理过程中的重要地位，对GIPG的资源规划问题进行研究。首先，从GIPG特点出发，构建资源规划流程，充分考虑PGM、专家以及社会公众的意见，保证各项目时刻与政策及规划一致；通过战略目标的获得及逐步分解至项目目标，保证各层目标之间的一致性。同时，详细阐明GIPG资源配置流程，为PGM提供借鉴。然后，对资源规划模型进行公式化表示并将战略目标与目标函数、约束条件紧密联系，保证目标与公式间的一致性。最后，引入具有更强全局寻优能力的IFA，其在解决GIPG资源规划问题时，能够遍历最优值且获得更优的全局最优值。基于以上分析，本文中所构建的资源规划模型合理性得到验证，能够对PGM提供借鉴和参考。但是，本文尚存在一些问题，将是进一步研究的重点，即专家组在分析国家、地区政策时，如何以定量方法提炼出GIPG战略目标，保证政策与战略目标之间的一致性。

参考文献：

[1]黄霆， 申立银， 赵振宇等. 我国政府投资项目管理的现状分析[J]. 建筑经济， 2005 （1）： 16-20.

[2]颜红艳， 张飞涟， 唐文彬等. 建筑企业项目群选择的ANP群体决策模型[J]. 科技进步与对策， 2011， 28（13）：38-42.

[3]高朋， 冯俊文. 企业项目群管理模式研究： 基于战略的视角[J]. 科技管理研究， 2009 （6）： 301-302.

[4]Yang X S. Firefly Algorithm， Levy Flights and Global Optimization[M].Research and Development in Intelligent Systems XXVI. Springer London， 2010. 209-218.

[5]尹贻林， 刘艳辉. 基于项目群治理框架的大型建设项目集成管理模式研究[J]. 软科学， 2009（23）：20-25.

[6]崇丹， 李永奎， 乐云. 城市基础设施建设项目群组织网络关系治理研究——一种网络组织的视角[J]. 软科学， 2012（26）：13-19.

[7]李彦苍. 改进蚁群算法在海洋工程群项目资源调度中的应用[J]. 中国管理科学， 2007，15（5）： 83-87.

[8]寿涌毅， 傅奥. 多目标资源受限项目调度的多种群蚁群算法[J]. 浙江大学学报（工学版）， 2010，44（1）： 51-55.

[9]郭研， 李南， 李兴森. 多项目多资源均衡问题及其基于Pareto的向量评价微粒群算法[J]. 控制与决策，2010，25（5）：789-93.

[10]李诗娴， 王雪青. 微粒群算法在工程项目多目标多资源均衡问题中的应用[J]. 科技管理研究，2010（17）：224-6.

[11]张贤哲， 方俊. 项目群资源优化的改进动态规划算法[J]. 武汉大学学报： 工学版， 2012， 45（3）： 405-408.

[12]张汉鹏， 邱菀华. 资源约束下多项目调度的改进遗传算法[J]. 中国管理科学， 2007， 15（5）： 78-82.

[13]董晓蓉. 蜂群算法求解资源受限项目调度问题及仿真[J]. 计算机仿真， 2013， 30（7）： 337-340.

[14]Yang X S. Nature-inspired Metaheuristic Algorithms[M]. Luniver press， 2010.

[15]Yang X S. Multi-Objective Firefly Algorithm for Continuous Optimization[J]. Engineering with Computers， 2013， 29（2）： 175-184.

[16]Liang R H， Wang J C， Chen Y T， et al. An Enhanced Firefly Algorithm to Mlti-Objective Optimal Active/Reactive Power Dispatch with Uncertainties Consideration[J]. International Journal of Electrical Power & Energy Systems， 2015（64）： 1088-1097.

[17]Apostolopoulos T， Vlachos A. Application of the Firefly Algorithm for Solving the Economic Emissions Load Dispatch Problem[J]. International Journal of Combinatorics， 2010.

[18]Kanimozhi T， Latha K. An Integrated Approach to Region Based Image Retrieval Using Firefly Algorithm and Support Vector Machine[J]. Neurocomputing， 2015（151）： 1099-1111.

[19]Wagan A I， Shaikh M M， Abro R. Wind Turbine Micrositing by Using the Firefly Algorithm[J]. Applied Soft Computing， 2015（27）： 450-456.

[20]Sahu R K， Panda S， Padhan S. A Hybrid Firefly Algorithm and Pattern Search Technique for Automatic Generation Control of Multi Area Power Systems[J]. International Journal of Electrical Power & Energy Systems， 2015（64）： 9-23.

[21]Brucker P， Drexl A， Mhring R， et al. Resource-Constrained Project Scheduling： Notation， Classification， Models， and Methods[J]. European Journal of Operational Research， 1999， 112（1）：3-41.

[22]Be ikci U， Bilge， Ulusoy G. Multi-mode Resource Constrained Multi-Project Scheduling and Resource Portfolio Problem[J]. European Journal of Operational Research， 2015， 240（1）： 22-31.

[23]Feng J C， Lei L I， Yang N， et al. Critical Chain Construction with Multi-Resource Constraints based on Portfolio Technology in South-to-North Water Diversion Project[J]. Water Science & Engineering， 2011， 4（4）：225-236.

（责任编辑：冉春红）