“综合与实现”总复习

蒋明玉

在小学六年的学习中，我们学到了不少数学知识和数学方法，这些知识和方法之间有什么联系呢？它们与我们的日常生活有什么联系呢？你能将其运用到生活中吗？

“综合与实践”内容涉及面广，题型千变万化，并且都带有一定的综合性。因此，同学们要仔细审题，从数学的角度全面提取数学信息，合理筛选有用的信息。

【例1】一个底面周长是6.28分米的圆柱形玻璃杯内盛有一些水，恰好占杯子容量的。现将两个同样的小球沉入水中，这时水面上升了6厘米，刚好与杯口齐平（如右图）。

（1）一个小球的体积是多少立方厘米？

（2）这个杯子的容量是多少升？

【分析与解】解决问题（1），同学们首先得明白升高部分水的体积就是两个小球的体积，从而确定解决思路：根据底面周长（单位需转化），算出底面积，再求出6厘米高的水的体积（也就是两个小球的体积），除以2就是一个小球的体积。

6.28分米=62.8厘米

62.8厘米？.14？=10厘米

3.14？0？0？？=942（立方厘米）

解决问题（2），同学们首先得想到6厘米相当于整个杯高的（1-），由此可以算出整个杯高，再根据底面积求出容积。

6鳎？-）=10厘米

3.14？0？0？0=3140（立方厘米）

可以看到，解决这两个问题，除了用到体积公式，还用到了上升部分水的体积等于两个球的体积的转化思想，同时用到了用分数除法解决问题的相关知识。

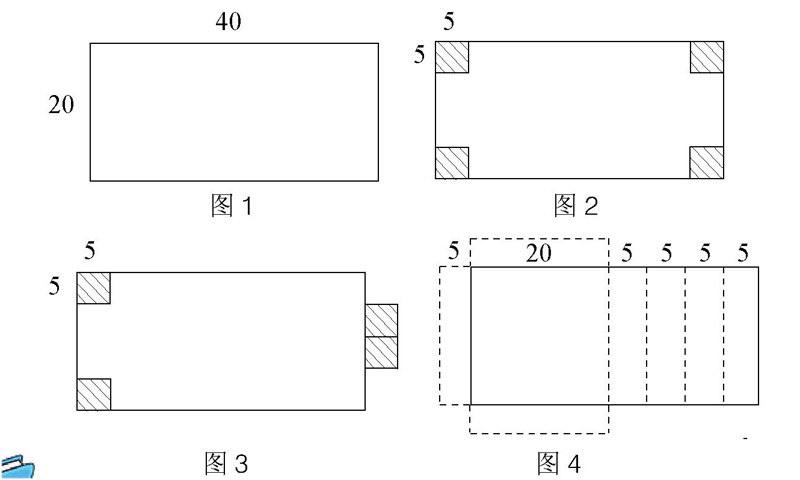
【例2】有一个长方形铁皮（如图1），长40厘米，宽20厘米。怎样将它做成一个高5厘米的无盖长方体盒子，并使它的容积变得最大？

图1 图2

图3 图4

【解法1】绝大部分学生这样思考：如图2，在铁皮的四个角上剪去4个边长是5厘米的正方形，然后做成长方体。这样做的体积是（40Ha5？）祝？0Ha5？）？=1500（立方厘米）。

【解法2】还有些学生这样思考：像解法1那样剪去4个小正方形，这样做太浪费了，如果像图3那样，将左边的两个小正方形铁皮割下来，然后补在右边，再做成一个长方体，那么它的体积是（40Ha5）祝？0Ha5？）？=1750（立方厘米）。

【解法3】少数善于创新的学生这样思考：如图4，将长方形的右边切下三个小长方形，分别补到长方形的上、下、左边，这样不仅材料无浪费，而且体积可以变得最大，即20祝？0-5？）？ =2000（立方厘米）。

【例3】一次，丁丁、宁宁、帅帅三位小朋友合租一辆出租车，讲好大家合理分摊车费。丁丁在全程的处下车，宁宁在全程的处下车，最后帅帅在终点下车。帅帅共付给司机90元钱。第二天，三人在一起算车费，丁丁、宁宁应给帅帅多少钱才合理呢？

【一般思路】丁丁、宁宁和帅帅所行的路程比为1∶2∶3，因此丁丁应付总钱数的，90？15（元）；宁宁应付总钱数的，90？30（元）；帅帅应付总钱数的。所以，丁丁、宁宁应分别给帅帅15元、30元。

【特殊思路】刚开始的路程，应付30元，应该由丁丁、宁宁、帅帅三人分摊，各人应付10元钱；中间的路程应付30元，应该由宁宁、帅帅两人分摊，各人应付15元钱；最后的路程应付30元，应该由帅帅一人拿出，应付30元钱。所以，丁丁应付给帅帅10元钱，宁宁应付给帅帅10+15=25（元）。

聪明的小读者，从数学的角度去分析，你认为哪一种方法更为合理呢？