自然数的四个属性

王建国

摘要：本文从人类对数的认识与发展，揭示了自然数的四个基本属性：数量属性；占位属性；进位属性；种属属性. 进而引出了一门新的数学——众数学及众运算，旨在从自然数的本质重新认识数学、诠释数学.

关键词：自然数；自然属性；众运算；众数学

人类对数的认识经历了漫长的历史过程：从一个人、一棵树、一株草、一只鸡、一条鱼、一头猪、一座山、一潭水、一把椅子、一张席子、一片森林…抽象出自然数“1”，标志着人类的文字记录、文明时代开始于对数的概念认识。从两只眼睛、两双手、两只胳膊、两条腿、两只脚…抽象出自然数“2”，使人类第一次认识到狩猎数量的增加与数的概念上数量增加是一致的对等的，从而使人类开始脱离于物质计数器（如贝壳、树枝、石子、竹片、结绳等），以纯粹的数字来计量计数。男女双方因喜悦组建家庭，女人分娩生产出小孩，导致家庭的人口数量增加到三个，随着人口数量的进一步再增加，形成了一个大家庭，同姓氏人口融合群居构成一个大家族，再由血缘关系、地域关系进而组成氏族、部落、公社或氏族联盟、部落联盟，最后形成独立于其它种族的一个个民族、一个个国家。一朵花、二朵花不能成为花园，三朵花以上便组成一个大花园；一棵树、二棵树不能成为一座森林，三棵树以上便可以组成一个大森林。所以独花不能开放，独木不能成林。人类便从物体的数量累加，抽象出自然数“3”。通过类比、延伸抽象出其它自然数：4、5、6、7、8…。那便是顺理成章的事。因此，老子在《道德经》中所言：“一生二，二生三，三生万物”。通过对自然数的重新认识，使我们知道自然数遵循物质的四个自然属性。

一、第一种属性是数量属性

这是自然数最本质的自然属性。自然数是一个抽象概念，独立于自然物质，有别于自然物质。具体体现在两点上：一是任何一个自然数都是由单位累积起来的；二是每一个自然数都有一个后继者。因此，1889年数学家皮亚诺以自然数的数量属性为基础，建立起了有关自然数的五条公理，这里限于篇幅略去。

自然数的数量属性，使物质集合（野兽、石子、花果、种子等）与数量集合建立起了一一对应的对等关系，标志着人类认识走向了数量化的认识之路，即数学之路。

自然数是人类认识事物、认识世界的一大进步。正因为有了自然数的这个数量属性（即与物体的数量对等性），使人类开始大面积地从宏观上把握认识事物、世界、宇宙。由于狩猎数量的增多、物品的剩余，人类开始思考如何按人进行分配物品，引发了“分数”的概念。古希腊毕达哥拉斯学派的成员希帕索斯（Hippias）发现了边长为1的正方形（单位正方形）的对角线与边长的不可公度性，被毕达哥拉斯学派集体封杀，据说把希帕亚斯抛入大海葬身鱼腹，但他的伟大认识和发现，没有被淹没，却载入了史册。后来，人们在解方程的问题上，提出了“负数”的概念，完成了无理数到实数再到复数的数的扩充，再由复数把数扩充到多元数、向量、矩阵、张量…体现了人类由有限到无限的认识过程。但是不符合唯物辩证法的认识过程：有限→无限→有限。也就是说数扩充后没有从无限认识回到有限认识中来，仅仅是向无穷方向层层推进。与复数有联系的多元数、向量、矩阵、张量等不是数，但是有运算，也是层层向无穷延伸逐步推进。

下面罗列归结为：

从数的扩充以及到实数公理系统的确立，人类对数的认识缺少了——把数由无限认识再回到有限认识的一个环节，这是数学认识与哲学认识共同缺失的链节。我们要做的就是建立一种新的数论来弥补上这个缺失，即在后面提出并建立的一门新的数学——众数学。这门新的数学可以完成数学由有限到无限的认识，再由无限到有限的认识。这与哲学上经常讲的“从实践中来，再到实践中去”，是一脉相承的。所以，数学老师以及数学书籍常常强调数学，“来源于生活，用之于生活”，是有着深刻的道理的。

二、第二种属性是占位属性

原始社会是狩猎、捕鱼、种植的农耕时代。每天打下的野兽、捕到的鱼、采摘的果实不仅有物品之分、数量之分，还要进行分配。否则，剩余要进行仓储管理、占据一定空间。其实，自然数在形成之初就具备了这种天然基因——自然占有空间位置。如243个人、243只鸡、243条鱼，抽象出数量“243”，如何再分配给每一个人呢？笔者通过认识思考发现：如果把每一个位置上的数字从整体上考虑，你就会发现把243各位数字相加得到一个新的数量结果，即2+4+3=9。

当然，你把243这个数字轮换变成了234、324、342、423、432。其各位数字相加得到的结果仍然是“9”。不妨你试试。这是巧合吗？这是偶然吗？显然，抛开这6个数字的形式，我们发现这6个数只是与2、3、4三个数有关。因为这三个数相加的结果就是：2+3+4=9。

在这里把243的各位数字相加得到的结果的运算，称之为“众数和”运算。

234的各位数字相减得到的结果是：-2-3-4=-9；把243这个数字轮换变成234、324、342、423、432，其各位数字相减得到的结果仍然是“-9”。

在这里把243的各位数字相减得到的结果的运算，称之为“众数差”运算。

234的各位数字相乘得到的结果是：2×3×4=24，再把24的各位数字相加得到的结果是：2+4=6；24的各位数字相减得到的结果是：-2-4=-6；24的各位数字相乘得到的结果是；2×4=8。把243这个数字轮换变成234、324、342、423、432，这五个数字的各位数字相加、相减、相乘得到的结果与234一样。

在这里把243的各位数字相乘得到的结果的运算，称之为“众数积”运算。把各位数字相除得到的结果的运算，称之为“众数商”运算。在这里，把众数和、众数差、众数积、众数商的几种运算，统称为“众运算”，其建立的数学统称为“众数学”。在这里暂且不讨论众数学的众运算规律与法则，有兴趣的读者可阅读笔者即将出版的《众数学》有关章节内容。

三、第三种属性是进位属性

同一个数可以用不同的进位制来表示。如：十进数35（10），可以用二进制表示为100011（2），可以用三进制表示为1022（3），可以用五进制表示为120（5），可以用八进制表示为43（8），可以用十六进制表示为23（16）。

一般情况下，整数运算的加减乘除是十进制运算，而对整数进行众数和运算，发现整数又是遵循严格的精准“九进制”运算，不重复、不遗漏。如观察整数1～45的众数和是1、2、3、4、5、6、7、8、9，这里是指最小的众数和，其中“9”相当于十进制中的“0”，只起占位和进位意义。

不同的进位制在不同的领域有着不同的用途。如二进制广泛应用在计算机方面；三进制主要用在军队编制方面；八进制广泛应用在计算机方面；十进制最为常用，主要应用在人们的日常生活中；十二进制主要应用在计算月份、时辰、天干地支；二十进制被玛雅文明使用过；六十进制主要应用在计算时间上（秒、分）。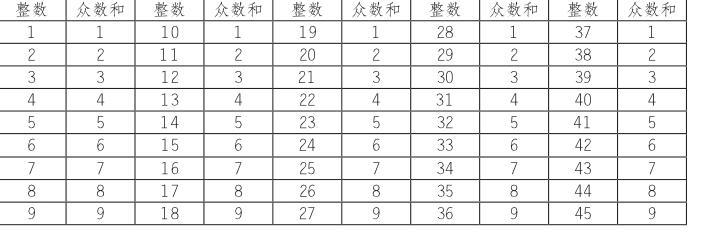

四、第四种属性是种属属性

不同民族不同国家曾使用过不同的进位制，但目前几乎所有国家均采用十进制。原始社会由于人们的认识水平低，对事物的划分比较肤浅。如按照性别把人分为男人与女人；按照事物的数量分为多与少；按照拥有物品把财产分为有与无财产；按照天气的温度分为冷与热。按照人的品格把人分为好人与坏人。按照数的奇偶性把整数分为奇数与偶数。按照数的大小性把整数分为正数与负数…

人类社会早期，人们认识到同一事物内部存在着相互对立的两个方面。如有无、多少、大小、方圆、曲直、繁简、聚散、长短、疏密、动静、虚实、刚柔、正负、高低…在一定范围内也存在着相互对立的事物或势力。如男与女、宾与主、敌与我、好人与坏人…无论多么复杂的物质或现象，这种普适规律——对立统一关系都存在。这种认识是朴素的、简单的、直接的，是一分为二的，这种既对立又统一的观点，在中国古代用阴阳二字来概括，称之为阴阳学说；在西方称之为对立统一规律。一分为二的阴阳概念抽象为集合概念，能分析揭示出自然界对立事物的根本变化原因及其根本规律。同样，用阴阳关系来代替对立事物的关系以及矛盾双方的相互关系，似乎很有概括性，一直沿用了中国上下几千年，并影响左右着中国传统文化以及世界文化。故《类经阴阳类》说：“阴阳者，一分为二也”。哲学上的“阴阳观”、“一分为二”的观点，与数学上的二进制算术系统相对应相联系，是哲学系统与数学系统的相互联系与统一。

参考文献

[1] 吴振奎，吴旻.数学的创造[M]。哈尔滨：哈尔滨工业大学出版社，2011.

[2] 张楚廷.数学与创造[M]。山东：大连理工大学出版社，2008.

[3] 探索学科科学奥秘丛书编委会.探索数学的奥秘[M].广州：广东世界图书出版公司，2009，10.

[4] （法）塞尔（Jean-Pierre Serre）.数论教程[M].丘成桐编，冯克勤译。高等教育出版社，2007，4.

[5] 林夏水.数学的本质·认识论·数学观[J].数学教育学报，2002，11（3）：26—30.

[6] 许啸天编著.老子[M]。北京：光明日报出版社，1995，1.