学习视角下创新型中小企业协同成长的粒子群优化分析

管仕平 商波

摘要：运用标准粒子群优化分析了不同类型学习因子对创新型中小企业协同成长的影响。结果表明：非对称线性学习因子对创新型中小企业协同成长有积极影响，但潜藏的知识流向断链可能会阻滞协同成长的持续性；惯性权重与学习因子的线性关系比非线性关系对创新型中小企业协同成长具有指引作用，同时，提出知识虚拟链接信息渠道有助于实现群体智能化学习，保持协同成长的稳定性；权重与学习因子的余弦函数关系说明了外界环境的剧烈变化不适宜创新型中小企业的协同成长。

关键词：学习因子；创新型中小企业；协同成长；粒子群优化

DOI：10.13956/j.ss.1001-8409.2016.08.07

中图分类号：F272 文献标识码：A 文章编号：1001-8409（2016）08-0029-05

1引言

中小企业作为社会经济单元的基本构成单位，在推动社会经济稳定发展方面起着不可替代的作用。企业发展过程的思维产生的氛围、资源的整合利用、寻求新组合以及承担和共享风险[1]的动态能力是企业获得自身成长优势的表现。而在创新型社会中，经济的转型发展主要依靠创新型中小企业，因为创新型中小企业是中小企业以持续性创新作为生存动力和发展目标的特殊群体[2]。

随着国家一系列创新政策的出台，创新型中小企业的异军突起有力地推进了国家创新经济的转型升级，而经济转型发展的持久性与创新型中小企业的成长密不可分。创新型中小企业考虑自身实际运营和发展状况，选择最佳的市场来提升融资效率[3～5]，融资创新对中小企业成长起重要作用[6]。与金融支持相关的创新环境政策是激励创新型中小型企业成长活力的重要外部因素[7，8]。而张玉明等认为知识和资本的双链要素是创新型中小企业成长的基因结构之一[9]，通过知识的积累和运用能够提高企业的创新水平[10]，它是为创新型中小企业持续成长制定政策的重要依据，并以科学规范的方法构建了创新型中小企业成长评价体系[11]。

已有研究从先验性理论和实证检验的视角研究了创新型中小企业成长的融资效率、经济环境与政策、成长结构以及评价体系等，也为本文提供了理论支撑和实践指导性。但这些研究更多地关注了创新型中小企业个体内部成长的本质特征，而在现实运营环境中，以知识为载体的中小企业个体成长关乎群体中的企业成长，并依企业个体的成长学习能力及群体之间的互动性来提升创新型中小企业的成长速度和竞争水平。基于此，本文从学习视角分析了环境中群体创新型中小企业的协同成长问题，并尝试运用粒子群优化方法与创新型中小企业的协同成长结合起来，对协同成长的过程及趋势进行仿真。

2创新型中小企业协同成长的标准PSO算法分析

粒子群优化（Particle Swarm Optimization， PSO）算法是在模拟鸟群或鱼群觅食过程中发展起来的群体协作的随机迭代搜索算法。PSO算法首先初始化一群随机粒子，设群体粒子数为m，在迭代时刻t，第i个粒子在d维空间以一定的位置Xi=（x1i，x2i，…，xdi）和速度Vi=（v1i，v2i，…，vdi）进行搜索，粒子搜索历史最优位置（pbest）和群体最优位置（gbest）分别表示为pi=（p1i，p2i，…，pdi）和pg=（p1g，p2g，…，pdg），i=1，2，…，N 。粒子在t+1时刻搜索到pbest和gbest时根据下式来调整自己的速度和位置。

vdi（t+1）=ω·vdi（t）+c1r1[pdi（t）-xdi（t）]+c2r2[pdg（t）-xdi（t）]（1）

xdi（t+1）=xdi（t）+vdi（t+1）（2）

其中，惯性权重ω描述了惯性对粒子搜索速度的影响，ω≥0；c1和c2为粒子向自身和群体学习的加速因子，c1，c2≥0；r1和r2为（0，1）的均匀随机数。当惯性权重ω，加速因子c1和c2为常数时，称为标准PSO算法。

为验证改进PSO算法在创新型中小企业协同成长分析上的性能，本文选择sphere函数作为粒

子的适应度函数，表达式为f（x）=∑ni=1x2i。一般而言，知识密集型企业的成长在受自身软条件约束时，促使企业之间产生需求特征的合作，尤其是领域内的劣势企业，合作化的研发行为为创新型中小企业提供从同伴企业中获得外部知识资源。伴随企业对知识的吸收、消化、模仿、运用的学习能力的提升，借助外部知识力量弥补技术劣势能力得到强化，新知识的跃迁促进企业对高技术产品研发独立性的形成，降低合作中对知识的过度依赖而造成额外损失。首先利用标准PSO算法分析创新型中小企业中粒子群的规模和迭代次数对创新型中小企业协同生长结果的影响。

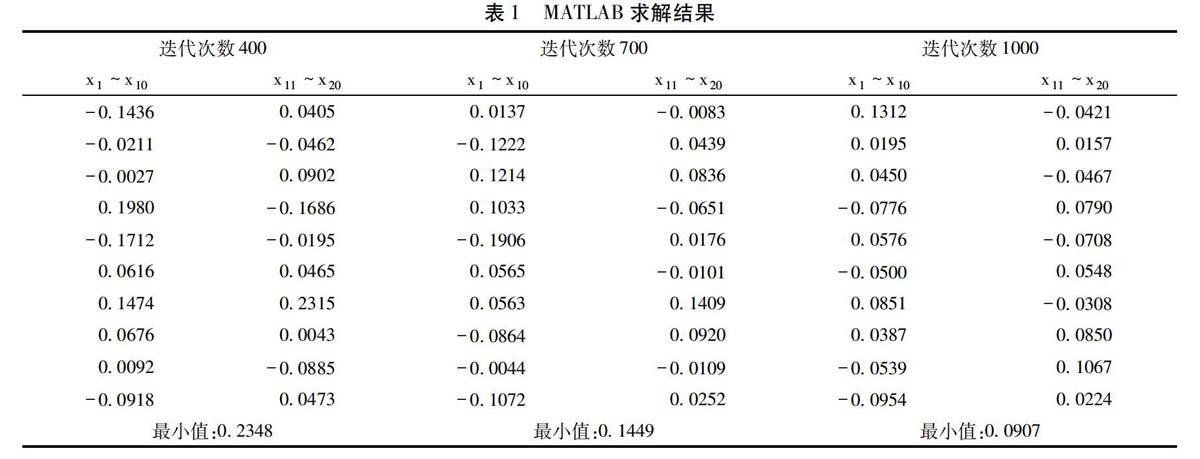
（1）粒子群迭代次数对创新型中小企业协同成长的影响。假设粒子群的规模N=20，权重ω=05，学习因子c1=c2=2，最大迭代次数分别为400，700，1000。运用MATLAB R2014a对结果进行分析，所得结果如表1所示。在参数不变情况下，一般随着迭代次数增加，求解的精度也不断提高，说明创新型中小企业与领域内优势企业保持长久稳定的战略合作伙伴关系，对创新型的小型企业的成长具有较好的协调性，中型创新企业的知识学习能力以及成长的独立性逐渐形成。在企业规模一定条件下，随着迭代次数的增加，不同层次企业之间成长的协同特征趋于明显，特别是对于知识和技术联系比较密切的科技创新型企业共同体，持续的相互协作是企业协同成长的基础。因为群体企业协作而产生的创新效益是集体效率的结果[12]。

（2）粒子群规模对创新型中小企业协同成长的影响。假设粒子群规模N=30，50，80，权重ω=05，加速因子c1=c2=2，最大迭代次数为100。对同一组参数重复运行20次，取仿真平均次数作为最终模拟结果，仿真如图1所示。不同粒子规模的函数适应度值差异较为显著，在迭代20次之前，规模较大的粒子群收敛速度较快，规模较小的粒子群收敛速度较慢，在迭代后期所有粒子规模的收敛速度趋于稳定。可见，在迭代次数一定前提下，规模对全局最优解有不同程度影响。对创新型中小企业而言，规模较大的企业群体，群内企业的技术人员、教育层次、研发经费等基础资源参差不齐，领域内的优秀企业较多，在协作前期具有较强的领袖能力，创新型中小弱势企业在此阶段学习能力较强，成长机会潜力大；在协作后期对集群中的其他企业有较强的协同能力，同时培养了企业成长的独立性。

3不同学习类型的创新型中小企业协同成长仿真与分析

以上是在学习因子和权重固定取值时粒子迭代次数和规模对创新型中小企业协同成长的影响。但企业在实际协同中的学习能力具有较大偏差，差异性学习对创新型中小企业协同成长的关键性是本文关注的焦点。在现有文献对标准粒子群改进学习因子研究的基础上，本文将讨论具有不同类型学习因子的企业学习能力对创新型中小企业协同成长过程的影响。这里不同类型的学习因子包括不含权重和带有权重函数的学习因子。

33不同学习类型的创新型中小企业协同成长分析

（1） 前面已经分析，固定学习因子整体寻优能力较非对称性学习因子较差，且非对称性学习因子最后一组取值最优。在创新型中小企业具有较强的自我改善和学习能力的条件下，企业内部个体之间的互动通过相互学习并以一定的技术支持形式实现协同思维的聚集[16]，对中小企业个体和创新型中小企业都会产生经济双赢的结果，协同成长也随之上升为创新型中小企业的战略性目标，以此为导向的中小企业协同成长的社会学习能力也得到加强。图2的自知学习比例在减少的同时社会学习比例在不断增加，这将弥补企业自身学习能力的缺陷而获得企业协同成长的优劣互补的外在优势，同时保持了群体的多样性，群体的多样性也决定了企业在专业化合作领域的协同成长前景。在先进和持续增长的领域中，大型企业占很小比例，而以创业精神为导向的中型企业的比没有创业和创新精神的小型企业成长速度要快，因为小型企业不具备资本、技术和能力在市场与之竞争。协作的双赢性和市场的竞争劣势使小型创新企业认识协作的主动性和保持持续吸引力，实现小型企业的创新与协同成长。然而对创新型中小企业而言，协同的持续性受到潜藏的知识要素的限制，知识的不足制约了协作的多变性，导致不同层次的中小型企业在协作和创新成长的过程中缺乏弹性，中型企业和小型企业在知识流向环节出现断链现象，协同成长可能出现阻滞，这也强调个体学习能力转向社会其他创新型企业学习的必要性。

（2） 带有权重函数的学习因子对创新型中小企业的协同成长有明显差异的影响。学习因子与权重的线性关系和非线性关系优化效果比较显著，如前文分析。创新型中小企业在初期呈非线性成长，企业成长并不会完全经过企业生命周期的每个阶段[17]，不同中小企业之间的协同思维的聚集程度通常处于无序状态，非线性权重使企业个体和社会学习能力出现非平衡状态，企业之间可能出现快速成长，也可能出现停滞甚至是衰败等不可预测的现象，因此，非线性惯性权重学习因子对创新型中小企业的协同性呈现不同的成长方式。本文认为中型和小型创新企业需要认识知识转移和创新的必要性，这种创新源于企业类型的多样性并实现知识信息的共享，企业协同多样性也实现了创新性，中型创新企业引领提升小型创新企业以保持他们之间协同多样性，最终实现持续的协同创新成长并保持成长的相对稳定性，对非线性权重学习因子具有较好的指引作用。但潜在的知识流向断链可能会阻碍企业的协同成长，而知识的虚拟链接渠道能够解决小型创新企业知识获取问题，打破地理空间屏障的缺陷，依赖现代网络化技术，建立知识传递的信息渠道，实现群体的智能化学习。余弦函数关系惯性权重学习因子模拟效果最差，惯性权重受到外界环境压力而出现震荡，导致学习因子失衡严重，在搜索中出现不稳定状态，难以实现创新型中小企业的协同成长。

4结论

本文基于学习视角，运用粒子群优化算法分析了创新型中小企业的协同成长过程。其中，标准粒子群优化算法分析了粒子群规模和迭代次数如何影响创新型中小企业的协同成长，但学习能力差异性在标准粒子群优化中并未得到充分体现，因此本文基于现有文献对优化算法的改进研究了不同学习类型创新型中小企业的协同成长，并得到以下结论：

（1） 非对称性学习因子使小型创新企业自我学习能力转向社会其他创新型企业学习，来弥补因个体知识的不足出现知识流向断链而制约企业协同成长持续性的缺陷。

（2） 非线性权重使企业个体学习能力和社会学习能力出现非平衡状态，因此，非线性惯性权重学习因子对创新型中小企业的协同性呈现不同的成长方式。

（3） 从长期看，线性关系的惯性权重学习因子对非线性关系的惯性权重学习因子有较好的导向性，并且知识虚拟链接的信息渠道也保证了群体智能学习的优势，有利于避免协同成长停滞的困窘，保持创新型中小企业协同成长的稳定性。

（4） 余弦函数关系的惯性权重学习因子受外界环境的波动不利于创新型中小企业协同成长。

参考文献：

[1]Bouncken R B， Plüschke B D， Pesch R， Kraus S. Entrepreneurial Orientation in Vertical Alliances： Joint Product Innovation and Learning from Allies[J]. Review of Managerial Science， 2014 （4）： 1-29.

[2]Nonaka I. The Knowledge Creating Company[J]. Harvard Business Review， 1991 （11-12）： 96-104.

[3]闻岳春， 王婧婷. 科技创新型中小企业的资本市场融资策略研究[J]. 科学管理研究， 2010， 28（2）： 107-112.

[4]秦军. 科技型中小企业自主创新的金融支持体系研究[J]. 科研管理， 2011，32（1）： 79-88.

[5]李芳， 王超. 创新型中小企业融资效率评价体系构建[J]. 统计与决策， 2014 （2）： 172-175.

[6]Cassia L， Colombelli A.Growth Factors in Medium-sized Enterprises： The Case of an Italian Region[J]. International Entrepreneurship and Management Journal 2010，6（4）：437-458.

[7]庄越， 李燕冰， 秦远建. 创新环境激励与企业成长：基于中部创新型企业的实证[J]. 科技进步与对策， 2012， 29（1）： 86-90.

[8]汪锋， 方炜俊. 促进我国科技型中小企业成长的对策研究[J]. 宏观经济研究， 2014 （11）： 20-29.

[9]张玉明， 段升森. 创新型中小企业基因结构模型实证研究[J]. 山东大学学报（哲学社会科学版），2013 （4）：1-9.

[10]Tan J. Innovation and Risk-Taking in A Transitional Economy： A Comparative Study of Chinese Managers and Entrepreneurs[J]. Journal of Business Venturing， 2001，16（4）： 359-376.

[11]张玉明， 梁益琳. 创新型中小企业成长性评价与预测研究——基于我国创业板上市公司数据[J]. 山东大学学报（哲学社会科学版）， 2011 （5）：32-38.

[12]Schmitz H. Collective Efficiency： Growth Path for Small-Scale Industry[J]. The Journal of Development Studies，1995，31（4）：529-566.

[13]Suganthan P N. Particle Swarm Optimizer with Neighborhood Operator[A]. Proceedings of the 1999 Congress on Evolutionary Computation[C]. Piscataway： IEEE， 1999. 1958-1962.

[14]Ratnaweera A， Halgamuge S. Self-Organizing Hierarchical Particle Swarm Optimizer with Time-Varying Acceleration Coefficients[J]. Evolutionary Computation， 2004， 8（3）： 240-255.

[15]赵远东， 方正华. 带有权重函数学习因子的粒子群算法[J]. 计算机应用， 2013， 33（8）： 2265-2268.

[16]Clark K A. Human Centered Design[M]. Berlin： Springer-Verlag GmbH Berlin Heidelberg， 2011.

[17]Gupta P D， Guha S， Krishnaswami S S. Firm Growth and Its Determinants[J]. Journal of Innovation and Entrepreneurship， 2013 （1）： 2-15.

（责任编辑：冉春红）