基于遗传算法优化的RBF神经网络在MBR膜污染仿真预测中的研究

汤佳 李春青

1 引言（Introduction）

水污染的预防和治理已成为当今世界日益严重的热点问题。膜生物反应器（MBR）作为一种将膜分离技术和生物反应技术相结合的新型高效污水处理技术，已被广泛应用于生活污水、有机废水处理等领域[1，2]。膜污染会影响MBR膜分离单元的性能，缩短膜的使用寿命，增加MBR系统的运行成本。因此研究膜污染的机理和预测控制方法，保证膜生物反应器能够在稳定的低耗能条件下获得较大膜通量是促进MBR推广应用的关键[3，4]。

目前在MBR膜污染领域，常用的多种预测模型都存在一些缺陷，如对膜污染机理分析不够透彻，预测精度差等问题。人工神经网络在预测领域有比较成熟的应用，而相比较传统的BP神经网络，RBF网络具有唯一最佳逼近的特性且无局部极小值的问题，可以做更精准高效的预测分析[5-7]。再引入遗传算法优化RBF神经网络的相关参数，弥补单一径向基网络模型的缺陷，就可以实现对膜污染更精准的预测。

2 RBF神经网络（RBF neural network）

人工神经网络（Artificial Neural Network，即ANN），是由人工建立的，以有向图为拓扑结构的动态系统，它从信息处理角度对人脑神经单元网络进行抽象化，建立简单模型，按不同的连接方式组成不同网络。人工神经网络以其特有的非线性适应性信息处理能力，使之在模式识别、自动控制、人工智能、预测估计等方面都有成功的应用，表现出了良好的智能特性。

径向基函数（RBF）神经网络是一种高效的前馈式神经网络，它由输入层、隐含层和输出层构成，具有其他前向网络所不具有的最佳逼近性能，并且结构简单，训练速度快。该神经网络采用RBF作为隐单元的“基”构成隐含层空间，将输入矢量直接映射到隐空间而不需要权值连接。当RBF的中心点确定后，映射关系也就随之确定。隐含层空间到输出空间的映射是线性的。

径向基神经网络的网络结构如图1所示。

RBF网络的激活函数采用径向基函数，以输入和权值向量之间的距离作为自变量，常见的隐含层节点的核函数为高斯函数。

（1）

其中，σ称为基函数的扩展常数或宽度，σ越小，径向基函数的宽度越小，基函数就越有选择性。

3 遗传算法（Genetic algorithm）

遗传算法（Genetic Algorithms，简称GA或GAs）是由密歇根大学Joho H.Holland教授及其学生于20世纪60年代末到70年代初提出的一种经典的智能算法。遗传算法是一种基于群体寻优的方法，具有全局搜索能力，初值无关性以及较快的收敛速度。具体过程如下：

Step1：采用随机的方法或者其他方法产生一个初始种群。

Step2：根据问题的目标函数构造适值函数（Fitness Function）适值函数用来表征种群中每个个体对其生存环境的适应能力。

Step3：根据适应值的好坏，不断选择和繁殖，基因通过交叉和变异得到更新。

Step4：若干代后得到适应值最好的个体即为最优解。

4 遗传算法优化的RBF神经网络（Optimization of

RBF neural network based on genetic algorithm）

RBF神经网络具有最佳逼近性和全局最优性，可以实现对MBR膜通量较为精确的预测。但是为了更好地选取相关参数，引入遗传算法对RBF神经网络的参数进行合理优化，其中包含四个参数，分别是误差、训练速度、最大神经元数目以及神经元的间隔，经过遗传算法寻优后得到的最优个体即为进行RBF神经网络训练涉及的最优参数。GA-RBF神经网络模型完成网络训练后，再采用仿真数据检测评估该网络的优化性能。

5 建立基于PCA的GA-RBF膜污染仿真预测模型

（A simulation model of GA-RBF membrane

pollution based on PCA is established.）

5.1 采用PCA进行模型输入参数选取

主成分分析（Principal Component Analysis，PCA）是一种掌握事物主要矛盾的统计分析方法，它通过矩阵特征值分析对初始数据进行线性空间投影，从多元事物中解析出主要影响因素，从而达到简化复杂的问题的目的。

膜污染的影响因素众多，通过减少RBF网络的输入数来简化RBF网络结构，从整体上提高RBF网络的性能。初选的六个膜污染影响因子为X={总阻力，MLSS，操作压力，COD，PH，温度}。

主成分分析法步骤为：

Step1：把初选的六个膜污染影响因子组成矩阵X。

Step2：对X数据标准化处理，得到标准化矩阵A。标准化后的数据阵每个列向量的均值为0，标准差为1，数据无量纲。

Step3：计算出协方差矩阵S。

Step4：计算协方差矩阵S的特征值λ与相应的特征向量u，然后将特征值由大到小排列得到特征值矩阵V和特征向量矩阵U。

Step5：对特征值矩阵V分析，计算出贡献率，确定主成分。通常选取贡献率为85%—95%的m个主成分进行综合分析。

通过计算选取出主成分贡献率在90%以上的三个污染因子即：MLSS、操作压力及温度，并以此作为RBF神经网络的输入层神经元。膜通量大小是表征膜污染程度的唯一指标，因此以膜通量作为RBF神经网络的唯一的输出层神经元。

5.2 建立基于GA-RBF的膜污染仿真预测模型

实验建立的GA-RBF膜污染预测模型如图2所示。

实验步骤如下：

Step1：对RBF神经网络的四个参数编码，为方便操作设定误差、训练速度为实数编码，最大神经元数目、神经元间隔为整数编码，所有编码得到的基因位串称为一个个体。

Step2：随机产生20个个体作为初始种群，构建初始的交配池。

Step3：执行RBF网络训练，得到误差百分比作为每个个体的适应度。个体间基因进行交叉和变异，保证基因多样性。

Step4：采用轮盘赌选择方式，筛选出适应度高的个体，淘汰掉适应度低的个体。

Step5：重复进行（3）直到结束循环，得到的个体为最佳个体。

Step6：训练完毕，最佳个体即为RBF网路最优的参数值，进行仿真测试，将实验数据与样本数据对比分析。

6 预测结果与实验结果对比分析（Comparison of

the predicted results with the experimental

results）

实验数据全部来自于石家庄市某MBR污水处理厂的实验以及工业生产的历史数据，统一采用的是孔径为0.2um的聚偏氟乙烯微滤膜处理污水方法。从实验数据中选取6组作为校验用样本，其余24组作为神经网络的训练样本。

遗传算法操作的初始参数为：选择种群规模：sizepop=20；最大进化代数：maxgen=10；交叉率：pcross=0.8；变异率：pmutation=0.5.RBF训练误差范围是1e-4-1e-3；最大神经元数目范围值是80—150；显示神经元间隔范围值是10—30；速度范围值是10—25。

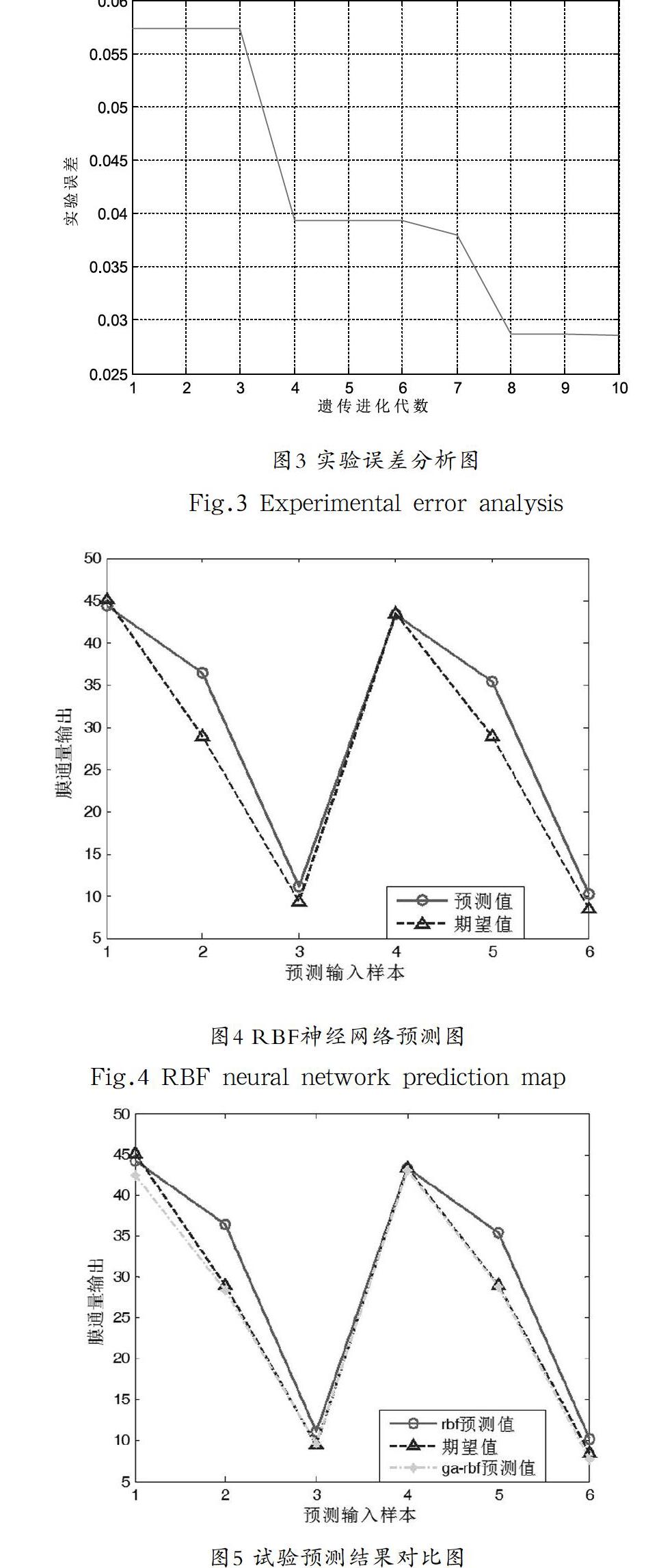
试验中得到遗传算法代数与误差曲线如图3所示。

图3显示了网络训练的误差随着遗传代数增加表现出来的变化趋势，随着进化代数增多误差降低，进化至第8代误差仅为0.02871，到第8代以后图像趋于缓和，基本已达到优化极限，实验收敛速度很快，优化效果明显。

为更好地体现优化效果，实验使用相同的样本数据进行测试，设置遗传算法进化到10代，分别对RBF网络和GA-RBF网络进行训练。首先得到基于RBF神经网络的预测结果，如图4所示，RBF网络的训练结果平均误差值为0.1130，已经能够完成初步的膜通量预测。然后再进行GA-RBF网络训练，预测结果对比如图5所示，经过GA优化参数之后的预测模型平均误差值仅为0.0275.准确度有非常明显的提高。实验结果表明，经过遗传优化过的RBF神经网络误差明显减小，得到的训练结果明显优于优化前的结果，预测精度较为理想。预测误差数据分析见表1。

7 结论（Conclusion）

由于膜污染过程具有非线性、参数时变性、随机干扰等复杂的机理，造成预测研究过程十分困难，本文在用主成分分析法简化输入参数的基础上，建立了RBF神经网络仿真模型，实验取得了良好的预测效果，误差符合实验标准。由于预测精度是否准确很大程度上取决于网络模型参数的选取，因此引入遗传算法，优化RBF网络相关参数，建立基于遗传算法优化的径向基函数神经网络预测模型并成功应用于MBR膜污染仿真预测中，研究结果表明，遗传算法优化后的RBF神经网络不仅提高了预测速度，还明显提高了预测精确度，从而能更好地实验对膜通量的检测和控制。整个实验过程具有一定的理论价值和实践意义，对MBR实际工程应该可以起到积极的指导作用。

参考文献（References）

[1] Yu Zhang，et al.Risk Assessment of Giardia from a Full Scale MBR Sewage Treatment Plant Caused by Membrane Integrity Failure[J].Journal of Environmental Sciences，2015（04）：252-258.

[2] Kun Li，et al.Advanced Treatment of Municipal Wastewater

by Nanofiltration：Operational Optimization and Membrane Fouling Analysis[J].Journal of Environmental Sciences，2016（05）：106-117.

[3] Hui Gong，et al.Membrane Fouling Controlled by Coagulation/Adsorption during Direct Sewage Membrane Filtration（DSMF）for Organic Matter Concentration[J].Journal of Environmental Sciences，2015（06）：1-7.

[4] 韩永萍，等.MBR膜污染的形成及其影响因素研究进展[J].膜科学与技术，2013（01）：102-110.

[5] 刘海萍.神经网络在CPI预测中的应用[A].中国管理现代化研究会.第五届（2010）中国管理学年会——市场营销分会场论文集[C].中国管理现代化研究会，2010：7.

[6] Guo ShengPeng，et al.Task Space Control of Free-floating Space Robots Using Constrained Adaptive RBF-NTSM[J].Science China（Technological Sciences），2014（04）：828-837.

[7] 王芹芹，雷晓云，高凡.基于主成分分析和RBF神经网络的融雪期积雪深度模拟[J].干旱区资源与环境，2014（02）：175-179.

作者简介：

汤 佳（1991-），女，硕士生.研究领域：MBR计算机模拟仿

真，大数据与云计算.

李春青（1962-），男，博士，教授.研究领域：MBR计算机模

拟仿真，大数据与云计算.