利用CORDIC算法提取脉内特征在FPGA上的实现

王炜珽 张文旭 陶东香

摘 要： 介绍了坐标旋转数字计算（CORDIC）算法的原理，给出了利用CORDIC算法提取信号脉内特征的迭代公式，在此基础上实现了用该算法的流水型迭代结构提取瞬时幅度、相位和频率的FPGA电路，解决了电路中的时钟与寄存器配置、数据的补码格式和相位累加等问题。通过在硬件芯片上的下载验证，表明电路结构合理、测试有效，满足设计要求。

关键词： 坐标旋转数字计算； 脉内特征； FPGA设计； 补码

中图分类号： TN79?34 文献标识码： A 文章编号： 1004?373X（2016）09?0001?05

Abstract：The principle of the coordinated rotation digital computer （CORDIC） algorithm is introduced. The iterative formula of the signal in?pulse characteristics extracted by CORDIC algorithm is proposed. On this basis， the FPGA circuit of extracting the instantaneous amplitude， phase and frequency by pipeline iterative structure of the algorithm was realized. The problems of clock and register configuration， data′s complementary code format and phase accumulation in the circuit were solved. The downloading verification on hardware chip shows that the circuit structure is reasonable， and test is effective. The circuit can satisfy the design requirement.

Keywords： coordinated rotation digital computor； in?pulse characteristics； FPGA design； complementary code

0 引 言

现代电子战中，提取辐射源信号脉内特征已成为许多电子侦查设备必备的功能，在此，仅以针对辐射源的测向技术为例，如比幅法需要知道脉冲的幅度信息、干涉仪法需要知道高精度的脉内瞬时相位和频率等。坐标旋转数字计算（Coordinated Rotation Digital Computer，CORDIC）算法是各种用来提取脉内特征的方法中较为常见的一种。该算法最早由J.Volder等人在1959年提出[1]，最初用它进行坐标变换。其基本思想是通过多次的迭代实现方向反复摇摆、数值逐次递减以逼近最终需要到达的角度，同时计算出与该角度有关的某些复杂函数运算结果。统一的CORDIC算法由J.S.Walther在1971年提出[2]，他将圆周、线性、双曲线三种算法和旋转、矢量两种模式统一到一个迭代方程中，为实现多模式共存的CORDIC算法硬件结构奠定了理论基础。CORDIC因能通过简单的移位和加减操作就能实现乘除、开方、三角变换、对数、指数等原本需要大量乘法器的运算，所以非常适合用FPGA设计实现[3?5]。

本文在分析圆周CORDIC算法原理的基础上，给出了利用CORDIC算法提取信号脉内特征的迭代公式，实现了用该算法的流水型迭代结构提取瞬时幅度、相位和频率的FPGA电路，在电路的设计过程中解决了电路中的时钟与寄存器配置、数据的补码格式和相位累加等问题。在信号分选、脉冲识别、辐射源定位等技术领域有一定的实用价值。

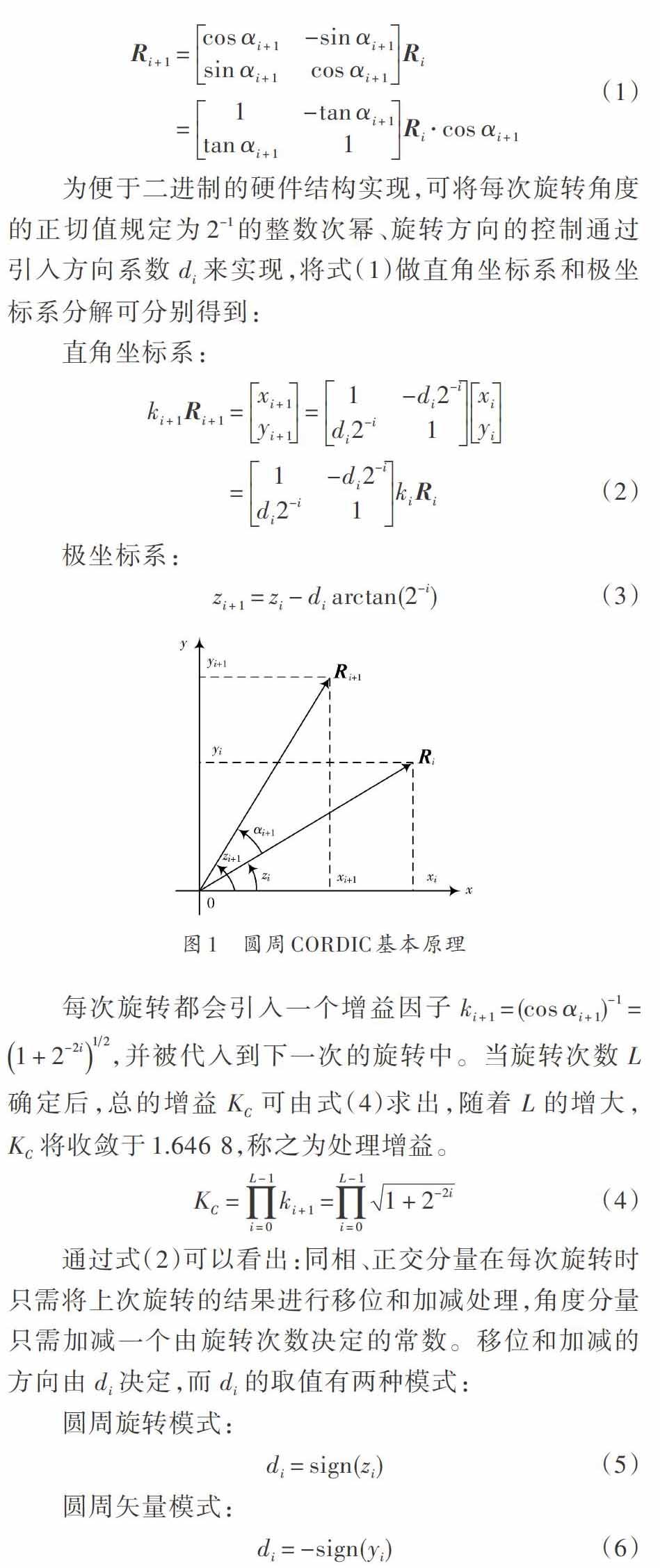
1 圆周CORDIC算法原理

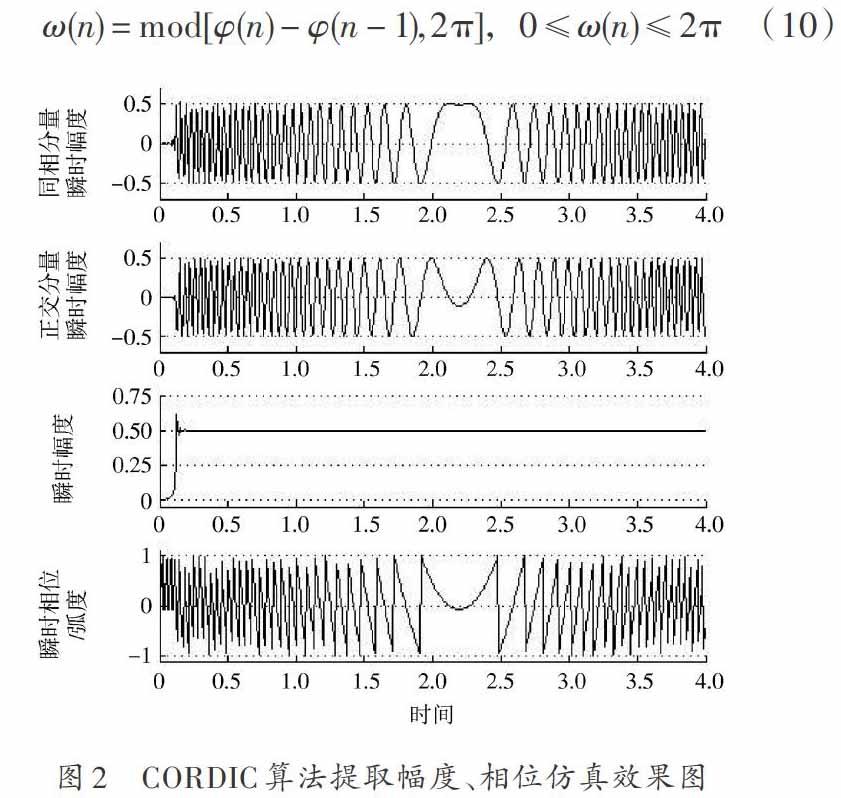
两种方法的主要区别在于：前者计算的瞬时频率仍在[-π，π]之间，但要加入判断电路；而后者的计算结果在[0，2π]之间，但在硬件电路中实现取模运算非常简单，有时甚至都不需要运算。由于圆周矢量模式CORDIC算法是对同相正交分量的计算，因此检测输出的频率可能出现负频率。这在硬件电路中用补码表示负数的方法即可解决，因为正余弦函数的周期对称特性使弧度在[0，2π]之间的取值本身就是其在[-π，π]之间取值的补码形式。分别利用式（9）和式（10）对2.1节仿真得到的瞬时相位求瞬时角频率，Matlab仿真结果如图3所示，其中图3（a）是存在相位卷绕的结果，图3（b）是用第二种方法解相位卷绕并将补码换算为正常负数的结果。从图3可见仿真结果正确地检测出了瞬时角频率，且符合上行LFM规律。

3 流水型CORDIC电路在FPGA上的实现

3.1 CORDIC算法迭代结构分析

CORDIC算法原理简单且易于理解和仿真，其难点在于如何设计合理的迭代结构来实现运算过程。迭代类算法通常有两种结构实现，即循环反馈型迭代结构（简称循环结构）和流水型迭代结构（流水结构）。循环结构是指通过单级算法单元实现多次迭代计算，将每次的计算结果反馈回本级进行下一次计算，如此循环[L]次以得到最终结果。流水结构是指通过多级算法单元实现多次迭代计算，将每级的计算结果输入到次级进行下一次计算，经过[L]级后得到最终结果。两种结构都必须在延迟[L]个时钟后完成计算。循环结构的优点是相对简单、硬件资源需求低；而流水结构恰恰相反。循环结构的缺点是每隔[L]个时钟才能进行一次计算，其运算速率是时钟频率的[1L；]流水结构没有此问题，其运算速率等于时钟频率。在实际应用中，应根据设计要求、结构特点，选择适当的实现结构[4]。圆周矢量模式CORDIC算法循环迭代结构如图4所示，其中符号“>>”表示移位。CORDIC算法的循环结构稍作改进即可作为流水结构的单级计算单元使用。

3.2 电路的具体设计

为保证提取的信号脉内特征的实时性，本文设计的CORDIC算法电路采用流水结构，设计过程中有以下三方面的技术问题需要重点解决：

（1） 时钟与寄存器的配置问题

考虑到一个时钟脉冲有两个边沿，当输入的同相正交数据在第0个脉冲上升沿到达时，为确保数据的稳定性，可利用第0个脉冲的下降沿承接并寄存输入数据，再到第1个脉冲上升沿到达时计算出结果并交给下一级的寄存器，此刻本级的寄存器便可准备好在第1个脉冲下降沿到达时承接新的数据。以此可实现数据的逐级流水计算，最终在延迟了[L]个脉冲上升沿后，CORDIC模块可输出与第0个脉冲上升沿数据对应的幅度和相位值。

由于VHDL语言规定一个寄存器只能受一个时钟脉冲边沿的控制，所以CORDIC模块每级运算单元设计了两个寄存器：一个是用来承接上级数据的流水寄存器，由下降沿控制；另一个是用来输出加减法结果的加法寄存器，由上升沿控制。差分模块同样需要两个寄存器，但他的输入数据寄存器可用CORDIC模块第[L]个加法输出寄存器替代，这也使差分模块只需CORDIC模块后的0.5个周期就可得到瞬时频率。各级寄存器与时钟的配置设计思路如图5所示。具体的实现电路中采取[L=12]的流水级，输出的幅度和相位数据相对于输入的同相正交数据延迟了12个时钟周期，瞬时频率数据则延迟了12.5个时钟周期。

（2） 实现用补码表示数据的问题

在大多数的A/D转换器和处理器中，负数都是用补码格式表示的[11]。补码的优点是做加定点数的减法运算时方便，无论正负数都可以直接相加，由于硬件电路中数的位数通常是固定的，所以加减运算时数据溢出会被直接去掉不影响最后结果[12]，这相当于做了一次求模运算。补码在表示负数和正数时均保持了数的单调增的变化规律，因此在做移位运算时要根据正负采取不同的方式。圆周矢量模式CORDIC算法每级迭代都是驱动正交分量[yi]向0逼近，所以对于正数采取数据右移并在高位补“0”的方法，对于负数仍是数据右移但在高位补“1”。其中[yi]可能在正负之间反复摇摆，所以对其移位要有判断程序，对[yi]正负的判断在求[di]时已经完成，拿来直接用即可。根据式（7）可知[xi]在第1级迭代结束后就已经被限定为正数了，且移位是从第3级迭代开始的，而其[xL]输出的是没有正负的幅度，因此对[xi]的移位都可按照正数执行。

对于[zi]而言，输入为0且没有移位的操作，只是根据[yi]的正或负逐级加上或减去一个相应的无极性原码表示的相位常数。由于弧度表示相位时本身就体现了补码的特性，用无极性的原码表示相位时可认为[φ（n）∈][0，2π]，用补码表示相位时可认为[φ（n）∈[-π，π]。]同理，对于差分模块的瞬时角频率也是如此，故无需做专门处理即可满足式（10）的要求。

针对输出数据的瞬时幅度采用无极性的原码表示，其值带有处理增益[KC，]且[KC]趋近于1.646 8，因此幅度的位数与[xi]的位数相同，本文所设计的电路不再做其他处理。

（3） 当[x0，y0]均为0时，瞬时相位的累加问题

可见，此时瞬时相位输出了一个非0的角度。对于同相正交分量来讲，[yi，xi]均为0的情况表示信号的瞬时幅度也为0，因此可引入一个幅度阈值，通过对比[xL]与阈值的大小消除该现象，同时该阈值可做噪声抑制门限用。

3.3 设计验证与分析

为适应更高的数据流速，实现运算速率与时钟频率的一致，本文针对图5所示的流水结构设计实现了FPGA电路并在Altera公司生产的EP4CE15F17C8芯片上进行了验证。该FPGA电路包括CORDIC和差分两个模块，均借助QuartusⅡ软件和VHDL语言设计[13]。

模块例化集成后的原理结构设计图如图6所示，其中CORDIC模块由12级流水单元构成。该电路输入端的[xi]（同相分量），[yi]（正交分量）和输出端的Aout（瞬时幅度）的位宽18位，输出端的pnout（瞬时相位）和fnout（瞬时频率）位宽20位，时钟clk外接100 MHz的频率源，与时钟异步的使能端en在高电平有效。[xi，yi，]pnout，fnout的数据格式为补码，Aout的数据格式是无极性的原码。

启动编译器，编译成功后得到的资源需求分析如图7所示，该电路结构占用了1 291个逻辑单元（LE），其中用到的寄存器为1 216个。

为了验证电路效果，输入仿真数据并利用Quartus Ⅱ自带的嵌入式逻辑分析仪（Signal Tap Ⅱ）进行数据的实时监测和采集。Signal Tap Ⅱ能够将测到的信号样本暂存在EP4CE15F17C8内嵌的RAM中，然后再通过JTAG端口将样本送回QuartusⅡ进行显示、分析，同时还能将采集的样本数据转换为txt格式文件输出，以供其他仿真软件如Matlab进行进一步的运算分析。输入数据如表2所示。

为了更好地观察时钟的上下边沿对模块的控制情况，利用一个数字锁相环将时钟倍频到200 MHz，每个clk时钟周期内包含2个样本采集点。启动Signal Tap Ⅱ，测试得到的波形效果如图8所示。图8中多位数据除Aout采用“Unsigned Line Chart”格式显示外，其他均采用“Signed Line Chart”格式显示。从波形效果上看，按表中数据依次循环的输入正交同相分量时，电路输出了瞬时的幅度、相位和频率。调幅信号的瞬时幅度为一频率较低的正弦信号，其他两种的瞬时幅度为一矩形脉冲信号。线性调频信号的瞬时相位、频率很好地体现了上行LFM的特点。从图8中还可以看出从同相正交分量数据输入到幅度、相位输出之间间隔24个样本采样点，即输出比输入延迟了12个clk时钟周期，但输出与输入数据的流速是相同的，这说明电路中实现了12级流水计算单元。

对比图9、图10可看出，图10中当[xi=0]且[yi=0]时，Aout输出为0，用其控制pnout输出为1（用于调试测试数据，使用时可设为0或其他值，阈值的选取视拟抑制的噪声幅度决定）。图10中当[xi=0]且[yi=0]时，输出补码格式的相位值为-495 666，折算成归一化弧度相位为-0.945 4π，这与式（12）一致。

4 结 论

本文设计的流水型结构电路实现了利用圆周矢量模式CORDIC算法检测中频脉冲信号的瞬时幅度、相位和频率，解决了时钟与寄存器配置、数据的补码格式和相位累加等问题。通过在硬件芯片上的下载验证，表明电路结构合理、测试有效，满足设计要求。

参考文献

[1] VOLDER J E. The CORDIC trigonometric computing technique [J]. IEEE transactions on computers， 1959， 8： 330?334.

[2] WALTHER J S. A unified algorithm for elementary function [C]// Proceedings of 1971 Spring Joint Computer Conference. [S.l.]： ACM， 1971： 379?385.

[3] 阎啸，秦开宇，高援开，等.基于CORDIC算法的频谱分析技术研究[J].电子科技大学学报，2006，36（3）：335?338.

[4] 张俊涛，王红仓.基于FPGA的CORDIC算法通用IP核设计[J].微计算机信息，2008，24（7）：238?240.

[5] 陈婧.改进型CORDIC算法的研究与实现[J].现代电子技术，2011，34（24）：165?167.

[6] 孔德元.针对正弦余弦计算的CORDIC算法优化及其FPGA实现[D].长沙：中南大学，2008.

[7] 金锋，佘世刚，王锴，等.基于System Generator的PM信号CORDIC算法鉴相的仿真与实现[J].现代电子技术，2013，36（5）：96?98.

[8] 闫温合，胡永辉，李瑾琳.应用于数字下变频中CORDIC算法的FPGA实现[J].时间频率学报，2014，37（1）：34?40.

[9] 胡爱明，胡可欣.一种雷达信号类型识别方法[J].现代电子技术，2006，29（14）：123?126.

[10] 张文旭.被动雷达导引头数字信道化接收机研究及实现[D].哈尔滨：哈尔滨工程大学，2009.

[11] 维纳 K 英格尔，约翰 G 普罗克斯.数字信号处理（Matlab版）[M].刘树棠，陈志刚，译.3版.西安：西安交通大学出版社，2013.

[12] 杜勇.数字滤波器的Matlab与FPGA实现[M].北京：电子工业出版社，2012.

[13] 陈欣波.Altera FPGA工程师成长手册[M].北京：清华大学出版社，2012.