Lyapunov stability and generalized invariance principle for nonconvex differential inclusions

Shu LIANG,Xianlin ZENG,Yiguang HONG

Key Laboratory of System s and Control,Academ y of Mathematics and System s Science,Chinese Academy of Sciences,Beijing 100190,China

1 Introduction

It is well-known that nonsmooth dynamics can be widely found in nature and engineering. On the one hand, various natural factors give rise to the nonsmoothness in systems modeling, such as mechanical friction and collision, hybrid or switching structure, and measurement constraints [1–4]. On the other hand, optimization and control in engineering design may yield nonsmooth structures, partially because nonsmooth systems often have more appealing dynamics and perform better to achieve desired goals, with representative examples, including sliding mode control, nonholonomic stabilization, and constrained optimization [5–8].

To study complicated nonsmooth dynamics, the socalled differential inclusion provides a fundamental and general theory [9], for definitions of nonsmooth solutions and their existence conditions as well as their convergence properties. Filippov was among the first to systematically study differential equations with discontinuous right hands with defining a class of nonsmooth solutions based on differential inclusions [10]. In fact,the key idea behind Filippov solutions is to introduce a convex differential inclusion determined by local vector fields.However,solutions in the Filippov sense may not be well-fitted for certain nonsmooth problem s,e.g.,stabilization of asymptotically controllable system s[11],which can be dealt with in the framework of general differential inclusions.There are also many other theories and tools for analyzing nonsmooth system s,such as differential-algebraic equations[12],differential variational system s[13],and projected dynamical system s[14].Among these,the differential inclusions p lay an effective role due to its flexible form and the capability to unify some other frameworks(see e.g.,[15]).

Stability is one of the most important dynamic properties for natural or engineering systems, and Lyapunovbased methods play a key and efficient role in stability analysis, which is related to invariance and attraction of the considered systems. It is known that various celebrated invariance principles further relax the technical requirement of the original Lyapunov’s theorem, and are applicable to systems with an equilibrium set. On the other hand, attraction analysis can provide convergence conditions and improve the estimation of the basin of attraction. Smooth Lyapunov functions are suitable candidates for a class of nonlinear systems (as a particular case for differential inclusions), indicated by a series of converse theories [16]. However, sometimes, at most Lipshcitz continuous rather thanC1Lyapunov functions can be guaranteed [17]. In order to deal with nonsmooth Lyapunov functions, nonsmooth analysis tools rather than the classical calculus have to be employed,such as the Dini derivative and upper contingent derivative [9]. Also, due to the set-valued characterization of the vector fields of nonsmooth systems and differential inclusions, a so-called set-valued derivative is developed to obtain a Lyapunov like stability criterion (see e.g., [18–20], and [21]). The key idea of these developments is to introduce the concept of Clarke generalized gradient (see [22] for definition and systematic introduction)to generate a quantitative characterization of the Lyapunov function along the system trajectories, which now becomes a standard technique called set-valued Lie derivative [2]. Moreover, corresponding extensions to the invariance principle have also been investigated (see e.g, works [19, 23, 24]). It is worthwhile to mention that most of these results are built on Filippov’s solutions and belong to the case of convex differential inclusions. Furthermore, they usually require the locally Lipschitz continuous Lyapunov function to be also regular or nonpathological [25]. In other words, in spite of rich theoretical developments built on convex differential inclusions or in the Filippov sense, most of the methods still suffer from certain restrictions

In practice,m any nonsmooth systems may give rise to nonconvex differential inclusions instead of convex ones.Furthermore,projection-embedded dynamics in advanced controller synthesis and/or continuous-time optimization algorithm s may also result in nonconvex differential inclusions.Although some works such as[9]have partially investigated such problem s,it proceeds the study by imposing continuous set-valued map assumptions that are very restrictive and could hardly be satisfied for many cases.Also,a Lyapunov stability criterion is presented in[9]for general nonconvex cases without any continuity assumption,w hose restriction is that it requires dominating the upper continent derivative of the Lyapunov function by another non-positive function.To our best know ledge,m any fundamental problem s with respect to stability analysis(particularly about invariance principles and attraction conditions)for general nonconvex differential inclusions remain to be solved.

with such a background,we are motivated to further investigate the stability problem s and focus on invariance principles and attraction conditions for nonconvex differential inclusions.In the nonconvex cases,we have to confront challenging technical obstructions in addition to the(convex)nonsmoothness.Note that many nice properties shared by the smooth nonlinear system s and convex differential inclusions do not hold any more in the absence of convexity.For example,the so-called solutions closure property[25]does not hold,which means that the limit of uniformly convergent sequence of system solutions may not belong to the set of solutions.Meanwhile,the continuous dependence of solutions on initial data,which is critical to characterize the limit property of solutions,can be hardly guaranteed,either.Additionally,how to qualify nonconvex differential inclusions of Lyapunov functions to analyze nonconvex differential inclusion system s is still a big challenge.These facts hinder us to develop a general invariance principle via routine techniques.

This paper is devoted to the study of above challenging problem s with respect to a class of nonconvex differential inclusions.We obtain a Lyapunov-based stability analysis,and then propose generalized invariance principle and attraction conditions.The contributions of our work include:i)a new stability criterion is derived by proposing a novel set-valued derivative in term s of simple directional derivatives,totally different from existing ones by using Clarke generalized gradients,which enables us to study locally Lipschitz continuous Lyapunov candidates without some well-known restrictions such as the function regularity;ii)a generalized invariance principle is proposed for nonconvex differential inclusions from a new viewpoint,and then is proved with overcoming the difficulties in the absence of convexity by means of refining the weakly invariance set as well as regularizing the stationary condition for a nonconvex differential inclusion with respect to the Lyapunov function;and iii)novel attraction conditions are given for the stability analysis for nonconvex system s,and the criteria may be used to estimate the attractive sets.Additionally,our results turn out to be consistent of some existing ones in a special case for the convex differential inclusions with regular Lyapunov candidates.

The rest of the paper is organized as follow s.Section 2 gives the basic concepts and problem formulation,while Section 3 provides the main results including the stability criterion,generalized invariance principle,and attraction conditions.Then Section 4 show s illustrative examples.Finally,Section 5 presents concluding remarks.

2 Preliminaries

In this section,we introduce concepts related to the solution and stability of differential inclusions and non-smooth derivatives(referring to[9,25]).

Consider a differential inclusion in the following form:

w hereFis an upper semicontinuous set-valued map from a domainD⊂Rninto subsets of Rnwith com pact values.Assume thatDis open and Br⊂Dfor somer＞0.

IfFis also with convex values,then(1)becomes a convex differential inclusion.Here we focus on the study of a class of nonconvex ones.

At first,we give a definition of the solution to a differential inclusion.

Definition 1LetI⊂R.A function φ(t):is said to be a solution to(1)onI,if φ(t)is absolutely continuous and˙φ(t)∈F(φ(t))for almost allt∈I.

For anyx0∈D,we denote bySx0the set of solutions to(1)with initial condition φ(0)=x0.SinceSx0may be empty set for somex0∈D,we denote byD0the set of all pointsx0renderingSx0≠ ∅.Then we make the follow ing basic assumption.

Assumption 1The setD0is dense inD,and any solution φ(·)is right maximal,i.e.,I=[0,+∞).

Next,we give definitions about various stability concepts for differential inclusions.

Definition 2Consider system(1).

a)A pointz∈DisLyapunov stableif,for every ε ＞0,there exists δ=δ(ε,z)＞0 such that

b)System(1)is said to besemistablewith respect toE⊂D,if for anyx0∈E∩D0and any φ(·)∈Sx0,the solution φ(t)converges to some Lyapunov stable point.

Rem ark 1In many engineering applications such as mechanical systems with rigid-body modes and consensus protocols for dynamical networks, the system dynamics have a continuum of equilibria. For systems possessing a continuum of equilibria, semistability [26]is a relevant stability notion. In fact, semistability is the property that every trajectory that starts in a neighborhood of a Lyapunov stable point converges to a (possibly different) Lyapunov stable point.

To study stability properties,we need to consider positive limit sets and weakly invariant sets.

Definition 3Letbe a measurable function andp∈X.

a)pis said to be apositive limit pointof φ(·)if there exists a sequence{tn},withsuch that

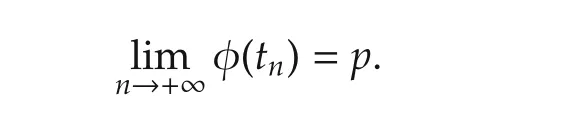
b)pis said to be analmost positive limit pointof φ(·)if

where μ is the Lebesgue measure in R.

Moreover,the set of all positive limit points of φ(·),denoted by Ωφ,is said to be thepositive limit setof φ(·).

The alternative namealmost cluster pointis used in[9].Any almost positive limit point is certainly a positive limit point.The converse becomes true when φ(·)is uniformly continuous as stated in Proposition 1[9,Page 312].The employment of almost positive limit point is for our analysis of attraction.

Definition 4A setMis said to be aweakly invariantset with respect to a system(e.g.,(1))if through each pointx0∈M,there exists a system solution lying inM.

Furthermore,we need a concept related to Lyapunov functions.

Definition 5A functionis said to be nonincreasing with respect to(1)if,for anyx0∈D0,φ∈Sx0and for allt1,t2∈[0,+∞),there holds

Moreover,Vis said to be a Lyapunov function if it is nonincreasing with respect to(1)and positive definite.

The following concept is required for the derivative of a Lyapunov function in our analysis.

Definition 6The right directional derivative of any functionVatxin the direction ofvis

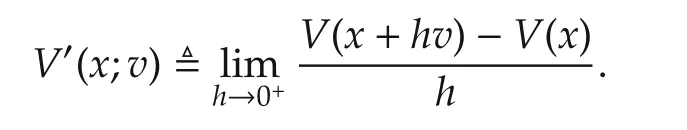
Let us define the following sets

whereF(x)is in(1).Note that the set ΘV(x),possibly empty,consists of all directional vectorsvsuch that bothV′(x;v)

,V′(x;−v)exist and satisfy the equation in(3).

In the stability studies,attraction analysis is important.Here we give the following preliminary know ledge for the related analysis.

Definition 7A set Γ⊂Rnof system(1)is said to beattractiveoran attractive setif its closure contains all possible positive limit sets.That is,

Or equivalently,for any φ∈Sx0,x0∈D0,

The following lemma is quite well-known.

Lemma 1(Proposition 5[9,Page 313])LetWbe a lower bounded,lower semicontinuous function from a bounded setL⊂Xto R.Ifx(·)is a measurable function from[0,+∞)toLsuch that

then any almost positive limit pointx＊ofx(t)satisfiesW(x＊)≤0.Moreover,ifW(·)is nonnegative,thenW(x＊)=0.

3 Main results

In this section,we show our theoretical results on stability and propose a generalized invariance principle of the nonconvex differential inclusion(1).Comparative analysis and possible extensions of existing results for the differential inclusion are also given.

3.1 Stability for nonconvex differential inclusions

In this section,we focus on the Lyapunov stability analysis of nonconvex differential inclusions,which is the cornerstone for the study of invariance and attraction of the considered dynamics.

The following lemma is very useful in the following analysis.

Lemma 2If there exists a continuous Lyapunov function for(1),then system(1)is Lyapunov stable atx=0.

ProofLetVbe the continuous Lyapunov function for(1).Given ε＞0,we can chooserε∈[0,ε)such that Brε⊂Dand moreover,there exist class K functions α1and α2,defined on[0,rє]such that

Define a set Ωβas

By choosing 0＜ β≤ α1(rε)andwe have

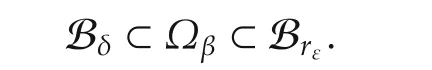
Then it follows from(2)that,for anyand any φ∈Sx0,there holds:

Then

Thus,system(1)is Lyapunov stable atx=0.□

According to Lemma 2,the system stability can be guaranteed if there exists a continuous(but possibly non-smooth)positive-definite function which is nonin-creasing with respect to the system solutions.It is preferable to characterize it in term s of the system vector field without actually solving φ(t).This observation gives rise to identify the monotonicity in(2)by checking the set-valued mapF.

The following result is related to the derivative of a Lyapunov function.

Lemma 3Letbe a solution to differential inclusion(1)and letbe a locally Lipschitz function.Then there exists a set Δ0of measure zero such that,for allt∈IΔ0,both˙φ(t)andexist.Moreover,we have

whereFVis in(4).

ProofSince both φ(·)andV(φ(t))are absolutely continuous,there is a set Δ0of measure zero such that,for allboth˙φ(t)andexist.BecauseVis locally Lipschitz continuous,we have that,fort∈IΔ0and a sufficiently sm allh＞0,there exists local Lipschitz constantl0＞0(depending ontandh)such that

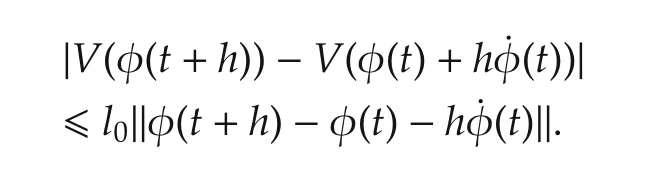
Then

which im plies that

Therefore,we have equality(5).Moreover,since

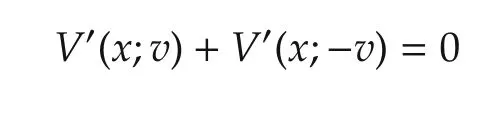
atx=φ(t),v=˙φ(t)forwe have inclusion(6).□

Rem ark 2It is true,in general,that locally Lipschitz continuousVmay have no directional derivative at som e pointx,renderingw here ΘV(·)is in(3).On the other hand,Lemma 3 tells us thatalmost everywhere.Furthermore,it is possible thatFV(x)=∅for somex,butholds fort∈Ialmost everywhere.

Throughout this paper,we define a new set-valued derivative ofVwith respect toFin(1)as

whereFV(x)is obtained fromF(x)through(4).

Now we are ready to state our stability criterion for system(1).

Theorem 1If there exists a positive definite,locally Lipschitz continuous functionsuch that,for allx∈D,

then system(1)is Lyapunov stable atx=0.

ProofIt follow s from Lemma3 and equation(5)that fort∈IΔ0,we have

Therefore,for anyt1≤t2,

ThenVis a Lyapunov function of(1),which im p lies that system(1)is Lyapunov stable according to Lemma2.□

Rem ark 3Theorem 1 asserts that the derivative criterion in(8)needs to be verified only at pointsx∈Rnwhereor equivalently,.In other words,points renderingcan be ignored without any danger for the stability test.This simplification will also sharpen the results as shown in Example 1.

Theorem 1 gives a stability criterion atx=0.For general concerns such as attraction and convergence,one needs to identify those attraction and/or convergence limit points,which may not necessarily be the only pointx=0.Thus we are motivated to develop invariance principles and attraction conditions for nonconvex cases in the following sections.

3.2 Generalized Invariance Principle for Nonconvex Differential Inclusions

Here,we present a generalized invariance principle with respect to the nonconvex differential inclusion(1).Before that,some lemmas are given in the following.

Lemma 4(Corollary 2[10,Page 77])LetFbe upper semicontinuous with com pact values.Then the limit of a uniformly convergent sequence of solutions to differential inclusion˙x∈F(x)is a solution to differential inclusion˙x∈co{F(x)}.

Lemma 5(Proposition 3,p.42,[9])LetFbe upper semicontinuous with com pact values.IfKis com pact,thenF(K)is com pact.

Now it is ready to present our result.

Theorem 2Letbe locally Lipschitz continuous,and nonincreasing with respect to(1),not necessarily positive definite.Suppose that,for somel＞0,the connected componentLlof level set{x∈Rn|V(x)≤l}such that 0∈Llis bounded.Let

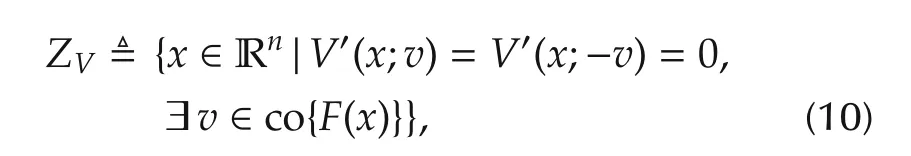
andMbe the largest subset ofwhich is weakly invariant with respect to co{F(x)}.Then the weakly invariant setMis also attractive.

ProofFor anyx0∈Ll∩D0and any φ(·)∈Sx0,it is to prove that

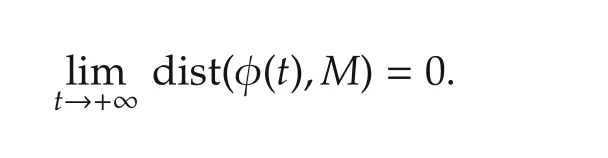
Let Ωφbe the positive limit set with respect to φ(t).It obviously follow s from the continuity of φ(t)and nonincreasing property ofV(φ(t))that φ(t)∈Ll.SinceLlis bounded,φ(t)is bounded.

Let us proveBecause of the definition ofLl,it holds Ωφ⊆Ll.It is left to verify Ωφ⊆clZV.

Firstly,we prove thatVis constant on Ωφ.Indeed,sinceV(φ(t))is decreasing and bounded from below(becauseLlis bounded),

for some constantc≥0.SinceV(·)is continuous,the image setis constant on Ωφ.

Second ly,we show that φ(t)is Lipschitz.Since φ(t)is bounded,is com pact.ThenF(K)is com pact according to Lemma 5.Hence,

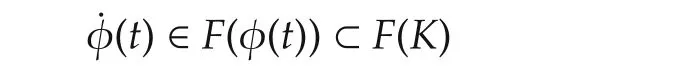
is bounded by some constant number ν ＞0.Since φ(t)is absolutely continuous,for anyt1,t2∈[0,+∞),we have

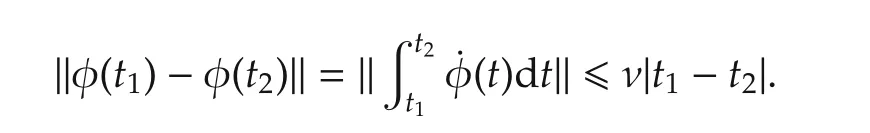
Third ly,for anyy∈ Ωφ,there existsuch thatLetFrom this definition and the fact that φ is bounded,{zn(t)}is uniform ly bounded.Besides,for any κ,τ ∈[0,+∞),there holds

which implies{zn(t)}is equicontinuous.Thus,there exists a subsequence{znk(t)}possessing a uniformly convergent limitz(t)according to the Arzela-Ascoli theorem.z(t)is also Lipschitz continuous according to(11),which implies that˙z(t)exists almost everywhere.It follow s fromz(0)=yandz(t)∈Ωφthat

almost everywhere.Moreover,recalling the differential inclusionit follows from Lemma 4 thatalmost everywhere.Therefore,from the definition ofZVin(10)and the above properties ofz(t),we havez(t)∈ZValmost everywhere.Letbe a sequence such thatz(τi)∈ZVfor alli.Sincez(·)is continuous,

As a result,Ωφ⊆clZV.

Finally,because

there holds Ωφ⊆M,which has completed the proof.□

Rem ark 4The key idea of our technique follow s from the fact that attraction property of a region/set is only determined by the system vector filed in the neighborhood of its boundary.Therefore,F(·)at stationary points as in(11)can be regularized via operations like co{·}operation to overcome technical difficulties in the lack of convexity.

Rem ark 5It follows from Lemma 3 that

holds almost everywhere.However,regarding to the invariance principle,it is not true in general to rep lace the co{F}in(10)byFor co{FV},becauseFmay have nonconvex values and co{FV}m ay be empty.

Next,we propose a semistability criterion to identify the convergence of solutions with respect to differential inclusion(1).

Theorem 3Given the setsLlandMin Theorem 2,if every point inMis Lyapunov stable,then(1)is semistable with respect toLl.

ProofIt follow s from Theorem 2 that for anyx0∈and any φ(·)∈Sx0,there holdsasand Ωφ⊂M,where Ωφbe the positive lim it set of φ.Since every point inMis a Lyapunov stable point of(1),we have thatz∈ Ω(φ(·))is Lyapunov stable.Then for any ε ＞0,there exists δ=δ(ε,z)＞0 such that for everyy∈Bδ(z)∩D0,any solutionof system(1)satisfies thatfor allt≥0.On the other hand,it follows fromz∈ Ω(φ(·))that there existsh=h(δ,z)＞0 such that φ(h)∈Bδ(z)∩D0.Therefore,φ(t)∈Bε(z)for allt≥h.Because ε ＞0 is arbitrarily taken,

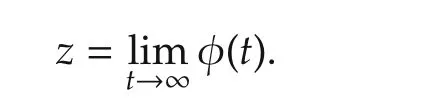
Hence,and Ω(φ(·))={z},wherezis a Lyapunov stable point.Sincex0∈Ll∩D0is chosen arbitrarily,it follow s from Definition 2 b)that(1)is semistable with respect toLl.□

3.3 Comparison and extension of existing results

To make a comparison,we first recall some notations with respect to Clarke generalized gradient utilized in Bacciotti’s results,and readers can refer to[19,22]for more details.

LetV:Rn→R be a locally Lipschitz continuous function.

Definition 8Clarke upper generalized directional derivative ofVatxin the direction ofv,denoted byV°(x;v),is defined as

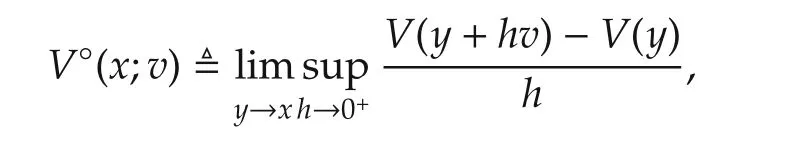
and Clarke lower generalized directional derivative,analogously denoted byV°(x;v),is

The next definition is about a well-known concept,regularity of functions.

Definition 9The locally Lipschitz functionVis said to be regular if the following two statements hold:

i)the right directional derivativeV′(x;v)exists for allv∈Rn,and

ii)there holds

The following two concepts are related to the derivatives of Lyapunov functions.

Definition 10Clarke generalized gradient ofVatxis the set

Definition 11Bacciotti’s set-valued Lie derivative ofVwith respect to a system vector field mapF(x)is defined as

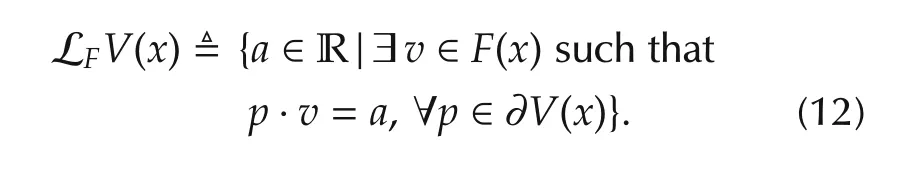
Bacciotti’s theorem for stability criterion of the convex differential inclusionis m axOn the other hand,our stability criterion in Theorem 1 is m axIt is in a position to give a comparison analysis.

Theorem 4IfVis locally Lipschitz and regular,thenfor allx∈Rn.

ProofSinceVis regular,there hold

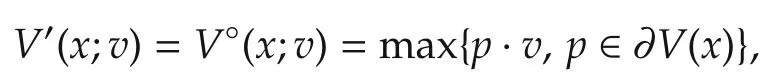
and

Therefore,the situation thatV′(x;v),V′(x;−v)exist and satisfya=V′(x;v)=−V′(x;−v)is consistent with In other words,if and only ifThus,allx∈Rn.□

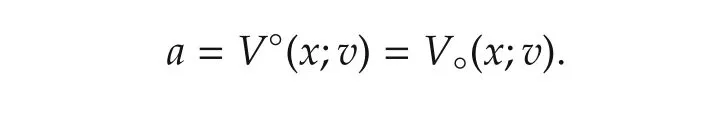
Rem ark 6Theorem 4 indicates that our stability result in term s of set-valued derivative(7)has indeed generalized Bacciotti’s stability criterion in terms of setvalued derivative(12)in two aspects.First,the result is applicable to both convex and nonconvex differential inclusions.Second,it removes the regularity restriction.If it is additionally assumed thatFis with convex values andVis regular,then Theorem 2 is consistent to the invariance principle in[19].

Finally,note that 1)the two set-valued derivatives LFV(x)andare equivalent under regularity condition,and 2)our results based on set-valued derivativeapply to noncovex differential inclusions.These two observations motivate us to explore whether the original stability criterion and invariance principle can be generalized for nonconvex differential inclusions and be still in term s of LFV(x).Actually,it is possible if the regularity is imposed,as shown in the follow ing corollaries.

Corollary 1The nonconvex differential inclusion(1)is Lyapunov stable atx=0 if there exists a positive definite,locally Lipschitz continuous,and regular functionV:D→R such that,for allx∈D,

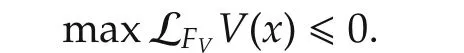
Corollary 2Letbe locally Lipschitz continuous,regular,and non-increasing with respect to(1),not necessarily positive definite.Suppose that,for somel＞0,the connected componentLlof level setsuch that 0∈Llis bounded.Takeand φ(·)∈Sx0.Let

andMbe the largest subset ofwhich is weakly invariant with respect to co{F}.Then the weakly invariant setMis also attractive.

Moreover,if every point inMis Lyapunov stable,then system(1)is semis table with respect toLl.

The proofs are omitted since they are similar to that for Theorem 4.

3.4 Attraction analysis

In the preceding subsections,we have presented a generalized invariance principle for nonconvex differential inclusions(1).However,as w e know,invariance set analysis is not the same as attraction analysis,and some essential difficulties caused by the lack of convexity have been overcome by regulations such as convex hull operation in(10).Then conservatism may result from these regulations.In special situations,clearer description about attractive set can be obtained under some strong conditions.Here,we focus on the case whenVis regular and the case when the derivative ofVis dominated by another functionW.

The following lemma is known for non-smooth analysis.

Lemma 6(Proposition 1.1[22,Page 70])LetVbe locally Lipschitz,then the Clark generalized directional derivativeV°(x;v)is upper semicontinuous as a function of(x,v).

The next lemma is important to our main result in this section.

Lemma 7Letx(·)be a bounded solution to system(1).Then,for any positive limit pointx＊ofx(t),there existsv＊such that

a)v＊∈F(x＊);

b)v＊is an almost positive limit point of˙x(t).

ProofSincex(·)is absolutely continuous,it is also uniformly continuous.Thusx＊is also an almost positive limit point ofx(t).That is,

Considering the time intervalwe have μ(In)=∞and

It follows from the similar proof of Theorem 4[9,Page 313]that there exists an almost positive limit pointv＊,nofx˙(t),anddue to the compactness.n

Since{v＊,n}is a bounded sequence,we take a subsequence{v＊,nk},whereassuch that

For any ε＞0,there isN＞0 such thatThen

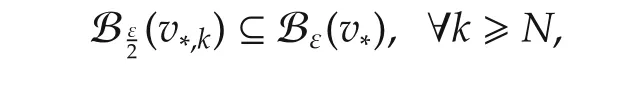
which im plies

Therefore,v＊is an almost positive lim it point of˙x(t).

Clearly,we can taketk∈Inkandassuch that

Note that the graph ofFis closed due to upper semicontinuity,we havev＊∈F(x＊),which completes the proof.□

It is ready to present our attraction result.

Theorem 5Consider the nonconvex differential inclusion(1),and let functionVand setsMandLlbe the same as given in Theorem 2.

a)IfVis regular and satisfies m axthen the setis attractive,where

b)IfVis not necessarily regular,but there exists a nonnegative lower semicontinuous functionWsuch that

Then the setM∩S2is attractive,where

Moreover,if every point in the identified attractive set(M∩S1and/orM∩S2)is Lyapunov stable,then system(1)is semistable with respect to the setLl.

ProofFirstly,letx(·)be any solution of(1),which is bounded according to Theorem 1.According to Lemma 7,for any positive limit pointx＊ofx(t),there existsv＊∈F(x＊)being an almost positive limit point of˙x(t).

Secondly,it follows from(9)that

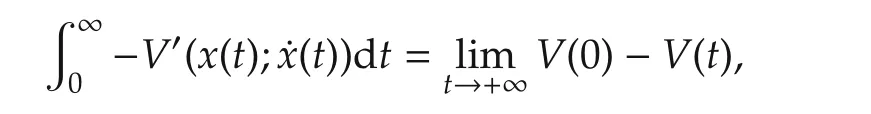
which is finite.IfVis regular,then−V′(x;v)=−V°(x;v),which is lower semicontinuous according to Lemma 6.Then,due to Lemma 1,V′(x＊;v＊)≥0.

Thirdly,since

which is upper semicontinuous with respect to(x,v),it is clear that

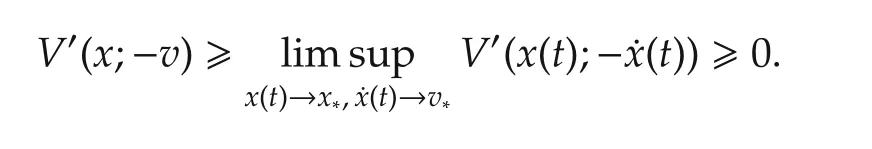
Thus,statement(a)holds.

Next,we move to(b).Due to(13),we have

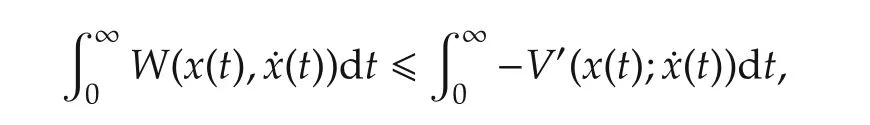
which is finite.According to Lemma 1,W(x＊,v＊)=0.

Finally,if any point in the attractive set is Lyapunov stable,then the semistability of system(1)can be guaranteed by a proof similar to that of Theorem 3.Thus,the proof is completed.□

Rem ark 7The criteria in Theorem 5 are in term s ofv∈F(x),different from the one in Theorem 2 withv∈co{F(x)}.Obviously,the former one is less conservative to estimate the attractive set.

4 Illustrative examples

In this section,we give two examples to illustrate our theoretical results.

Exam p le 1(Exam p le 1 of[19])

Consider differential inclusion(1)withF(x)in the following non-smooth form:

where

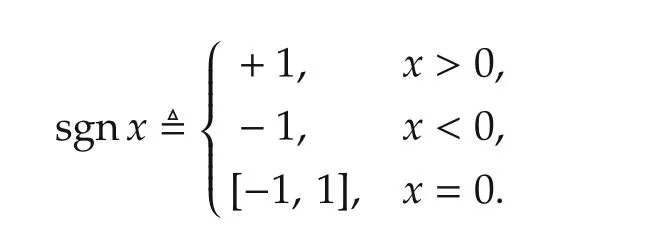
Let us considerV(x1,x2)=|x1|+|x2|.We have

and

Then there holds

SinceV′(x;v)≤0,system(1)is Lyapunov stable atx=0.As remarked in[19],the upper right Dini directional derivative atx=(0,x2),v=(−1,1)isD+V(x;v)=2＞0,by which the test is inconclusive.

Exam p le 2Consider differential inclusion(1)withF(x)as follows:

where

ThenF(x)is upper semicontinuous with compact values,and nonconvex at(0,0).Let us considerV(x)=|x1|+|x2|.We haveV′(x;v)as same as in Example 1,and

Then

Sincesystem is Lyapunov stable.In addition,we obtain

and

Thus,it is verified thatas Theorem 4 states.In addition,point(0,0)is attractive,which can be identified by Theorem 2.

5 Conclusions

In this paper,we considered a class of nonconvex differential inclusions with providing a stability result for locally Lipschitz continuous Lyapunov functions.Especially,we paid much attention to a generalized invariance principle and attraction conditions for the nonconvex dynamics.To solve the problem s,w e introduced a set-valued derivative for non-smooth system s and non-smooth Lyapunov functions.Also,we demonstrated that our results are consistent with the existing ones in the case of convex differential inclusions with regular Lyapunov functions.These achievements show potential applications of our results in a broad range of science and engineering fields.

References

[1]D.E.Stewart.Rigid-body dynamics with friction and impact.SIAM Review,2000,42(1):3–39.

[2]J.Cortes.Discontinuous dynamical system s:A tutorial on solutions,non-smooth analysis,and stability.IEEE Control System s Magazine,2009,28(3):36–73.

[3]G.Shi,Y.Hong.Global target aggregation and state agreement of nonlinear multi-agent system s with switching topologies.Automatica,2009,45(5):1165–1175.

[4]M.S.Branicky,V.S.Borkar,S.K.Mitter.A unified framework for hybrid control:model and optimal control theory.IEEE Transactions on Automatic Control,1998,43(1):31–45.

[5]D.Feijer,F.Paganini.Stability of primal-dual gradient dynamics and applications to network optimization.Automatica,2010,46(12):1974–1981.

[6]V.Utkin.Sliding Modes in Control Optimization.Berlin:Springer,1992.

[7]R.W.Brockett.Asymp totic stability and feedback stabilization.Differential Geometric Control Theory.R.W.Brockett,R.S.Millmann,H.J.Sussmann,eds.Boston:Birkhauser,1983:181–191.

[8]P.Yi,Y.Hong,F.Liu.Distributed gradient algorithm for constrained optimization with application to load sharing in power system s.System s&Control Letters,2015,83:45–52.

[9]J.P.Aubin,A.Cellina.Differential Inclusions.Berlin:Springer,1984.

[10]A.F.Filippov.Differential Equations with Discontinuous Righthand Sides.Boston:Kluwer Academic Publishers,1988.

[11]F.H.Clarke,Y.S.Ledyaev,E.D.Sontag,et al.Asymptotic controllability implies feedback stabilization.IEEE Transactions on Automatic Control,1997,42(10):1394–1407.

[12]K.E.Brenan,S.L.Campbell,L.R.Petzold.Numerical Solution of Initial-value Problem s in Differential-algebraic Equations.New York:North-Holland,1989.

[13]J.S.Pang,J.Shen.Strongly regular differential variational systems.IEEE Transactions on Automatic Control,2007,52(2):242–255.

[14]A.Nagurney,D.Zhang.Projected dynamical System s and Variational Inequalities with Applications.New York:Springer,1995.

[15]B.Brogliato,A.Daniilidis,C.Lemar´echal,et al.On the equivalence between complementarity system s,projected system s and differential inclusions.System s&Control Letters,2006,55(1):45–51.

[16]H.K.Khalil.Nonlinear System s.3rd ed.Upper Saddle River:Pearson Education,2002.

[17]L.Rifford.Existence of Lipschitz and semiconcave control–Lyapunov functions.SIAM Journal on Control&Optim ization,2000,39(4):1043–1064.

[18]D.Shevitz,B.Paden.Lyapunov stability theory of non-smooth system s.IEEE Transactions on Automatic Control,1994,39(9):1910–1914.

[19]A.Bacciotti,F.Ceragioli.Stability and stabilization of discontinuous system s and non-smooth Lyapunov functions.Esaim Control Optimisation&Calculus of Variations,1999,4:361–376.

[20]E.Moulay,W.Perruquetti.Finite time stability of differential inclusions.IMA Journal of Mathematical Control&Information,2005,22(4):465–475.

[21]A.Bacciotti,L.Rosier.Lyapunov Functions and Stability in Control Theory.2nd ed.Berlin:Springer,2005.

[22]F.H.Clarke,Y.S.Ledyaev,R.J.Stern,et al.Nonsmooth Analysis and Control Theory.New York:Springer,1998.

[23]R.G.Sanfelice,R.Goebel,A.R.Teel.Invariance principles for hybrid systems with connections to detectability and asymptotic stability.IEEE Transactions on Automatic Control,2007,52(12):2282–2297.

[24]N.Fischer,R.Kamalapurkar,W.E.Dixon.LaSalle-Yoshizawa corollaries for non-smooth systems.IEEE Transactions on Automatic Control,2013,58(9):2333–2338.

[25]A.Bacciotti,F.Ceragioli.Nonpathological Lyapunov functions and discontinuous Carath´eodory system s.Automatica,2006,42(3):453–458.

[26]S.P.Bhat,D.S.Bernstein.Nontangency-based Lyapunov tests for convergence and stability in system s having a continuum of equilibria.SIAM Journal on Control&Optimization,2003,42(5):1745–1775.