山区复杂大流域地貌发育阶段判识方法及应用

段书苏, 姚令侃,2,3, 郭沉稳

(1.西南交通大学 土木工程学院，610031 成都； 2.抗震工程技术四川省重点实验室 道路与铁道工程抗震技术研究所，610031 成都；3.高速铁路线路工程教育部重点实验室，610031 成都)



山区复杂大流域地貌发育阶段判识方法及应用

段书苏1, 姚令侃1,2,3, 郭沉稳1

(1.西南交通大学 土木工程学院，610031 成都； 2.抗震工程技术四川省重点实验室 道路与铁道工程抗震技术研究所，610031 成都；3.高速铁路线路工程教育部重点实验室，610031 成都)

摘要:为确定山区复杂大流域的地貌发育阶段及其在地震、暴雨等触发条件下的灾害区域严重程度. 基于地貌循环理论和山区复杂大型流域的分阶段发育的理论，将斯特拉勒积分的计算方法与坡降指标(SL指标)结合，以确定山区复杂大流域的发育阶段. 利用DEM(digital elevation model)和ArcGIS技术，计算发育阶段并据此评价崩塌滑坡在触发条件具备时的区域严重程度. 在山区复河流复杂大流域内，分支小流域的斯特拉勒积分的变化点，SL指标的突变点均可以作为发育阶段的分界点；在同一发育阶段内，斯特拉勒积分值分布集中，整个发育阶段的斯特拉勒积分可以作为处于这一发育阶段的所有分支小流域发育阶段的代表值. 处于幼年晚期和壮年期的流域，斯特拉勒积分处于0.45～0.6之间，崩塌滑坡最严重.

关键词:侵蚀循环理论;河流分阶段发育理论;斯特拉勒积分;坡降指标SL;地震触发崩塌滑坡

2008年5月12日四川省汶川县发生Ms8.0级大地震，2013年4月20日，四川雅安芦山县发生Ms7.0 级强震. 2015年4月27日，尼泊尔发生Ms8.1级大地震. 地震触发的崩塌滑坡灾害的研究引起了各国学者的重视. 触发滑坡的自然因素主要有两种，其一是水的作用，其中降雨滑坡约占该类滑坡的90%，是较为常见的灾害现象；其二是地震，可在短时间内触发大量、密集的崩塌滑坡，但具有发生频率低的特点. 例如，根据国土资源部和中国地质调查局始于1999年的地质灾害调查表明，四川省雅安市雨城区、名山县、荥经县、宝兴县地区降雨滑坡共计245处[1]；但在2013年的“4.20”芦山地震时，一次性引发了1 754处滑坡(震区包含了上述4个县市以及天全县和芦山县的大部分地区). 地震触发崩塌滑坡的分布，现在普遍认为主要受到发震断层、地形地貌、岩性这三大因素的控制[2]. 国内外很多学者根据实震资料的统计结果，依据综合指标法、确定性系数分析法、Newmark累计位移法等，得出了上述因素对崩塌滑坡的影响作用. 其中，1980年美国学者Keefer[3]、Rodriguez等[4]对世界范围内的滑坡进行统计，归纳了地震滑坡分布与震中距、岩性等之间的关系；2000年，乔建平、王余庆等[5-7]等运用综合指标法对影响地震滑坡的各种因素进行了区分和定量化，进而对区域地震滑坡进行评价分级；许冲等[8-9]利用ArcGIS技术平台，采用综合指标法对玉树、汶川地震滑坡危险度进行了评价. 这些均是从统计层面开展的研究工作，研究结论反映了历史地震崩坍滑坡的统计特性，成果的普适性受统计样本代表性的限制. Newmark累计位移法[10]是从力学层面研究斜坡稳定性的最具代表性的成果. 此方法利用滑坡产生的累计位移与临界加速度、Arias强度之间的相关关系，获得研究区域内任意坡体的近似累计位移量值，用于地震触发的崩塌滑坡的危险性评估. 但Newmark模型不但依赖统计样本代表性，而且所需要的参数较多(包括滑坡深度及滑动面形状、滑动面粘聚力、内摩擦角等).

上述地形地貌对滑坡分布的影响只停留在现象统计的阶段或者要依赖于现象统计建立回归模型，并没有相应的理论解释. 本文利用地貌学大型河流的多级分阶段发育的原理，解释在一复杂大型流域内地形的不同发育阶段. 结合处于某一发育阶段的流域内坡体偏离临界坡的程度不同而定性地评估流域内斜坡重力灾害的严重性. 进而解释地形地貌对崩塌滑坡灾害的控制性作用,并为线路选线提供参考.

1河流流域的发育理论

1.1地貌的侵蚀循环理论

基于发生学的理论，Davis在1899年首次创立了侵蚀循环学说(theory of the cycle of erosion)，将循环过程中的地形发展分为3个阶段：地形起伏不大，河间地广阔平坦的幼年期，地面主要由谷坡和狭窄的分水岭组成的壮年期，和具有残丘的准平原的老年期[11].

按照Davis绘制的河流地貌发育图式，地貌发育循环过程中的地形变化如图1所示. 图中横轴表示时间轴，纵轴表示海拔高度，曲线BDFH、ACEG分别代表原始地面的河谷的平均高度和分水岭的平均高度随时间的变化. 虚线表示地壳短暂快速的抬升阶段，则AB表示原始地形的起伏程度. 由图可知，整个幼年期阶段直至壮年中期，河谷强烈迅速下切，河谷平均海拔持续下降，而河谷之间由比较宽广的分水地发展为分水岭，平均海拔高度没有显著变化，因此原始地面的起伏程度迅速增加，至壮年中期，起伏程度达到最大，分水岭与河谷之间的高差达到最大值EF. 壮年期晚期和老年期阶段，河谷已经接近侵蚀基准面，高程基本上没有太大变化，分水岭受到外营力的侵蚀而不断的降低，分水岭变得浑圆低矮，直至准平原.

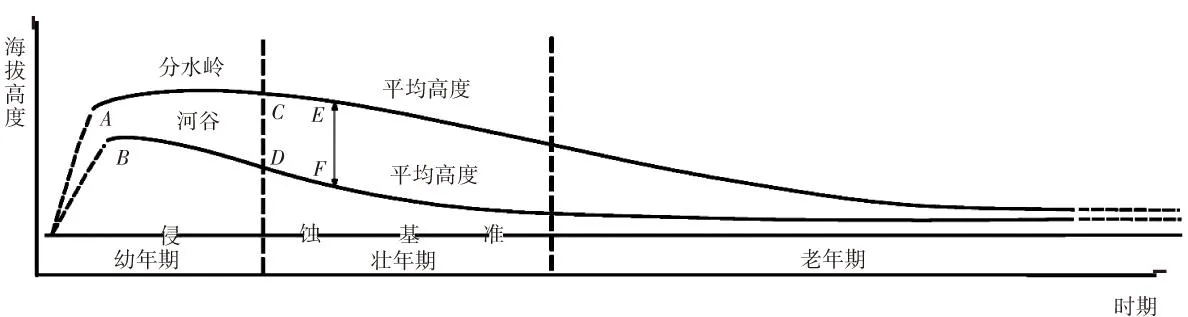
图1　Davis河流地貌发育图(根据W. M. Davis)

地貌的形成和发展是内、外营力相互作用的结果，两者彼此消长、相互作用、相互影响. 内营力趋向于使山体隆升，增强区域起伏程度，使山体愈发陡峻；外营力趋向于使山体高度降低、削平，减弱区域起伏程度，使山体愈发浑圆低矮. 内营力是系统的，来自全球性的板块构造，其速度可以认为是确定的，而外营力是变化的. 在新构造运动强烈的山区，山地隆升速度每年可达几毫米至十几毫米，山体剥蚀降低的速度小于地块隆升速度；但随着山体高度的上升，带来侵蚀基准面的降低，进而加大地表物质的重力作用和水流的下切侵蚀与搬运作用，外营力效应随之增强. 外营力效应绝对量的增加必将导致内外营力作用的相对差距缩小，当地貌演化处于内外营力相当的阶段时，由于二者对山地地貌塑造的反向效应，山体坡度最大只能达到一个特定值，即所谓的临界坡度(对应于图1的EF时期). 这就是在一个侵蚀循环内，地貌经历幼年期、壮年期、老年期的同时，流域内的坡体相应经历向临界坡度发展、达到临界坡、偏离临界坡的演变过程的物理机制.

从构造地貌学角度，临界坡是一个区域内斜坡系统能相对长期保持的极限坡度；从工程角度，对于滑坡工点，即为下滑力与抗滑力处于极限平衡状态时对应的坡度. 处于临界坡的斜坡系统，在地震、降雨等外界扰动下，极易发生失稳破坏，造成大规模的崩坍滑坡；反之，坡度小于临界坡时，斜坡系统就具有了一定的安全裕度，而且偏离临界坡度越远，安全裕度越大，发生崩塌滑坡可能性越小.

1.2山区复杂大流域的分阶段发育

上述的戴维斯(W. M. Davis)侵蚀循环学说，描述了特定构造条件下河流地貌随时间演化的过程. 但是，对于山区大型流域的不同区段，并不是同时发育的，也就是说在同一时期，同一流域内存在不同发育阶段组合的现象. 与此相对应的，各个河段形态组合而成的纵剖面也就具有相应的形态[12-13]，本文用纵剖面的组合形态说明这一过程. 假设构造抬升之前始准平原上先成河的纵剖面、支沟剖面均处于均衡状态下，如图2中曲线0所示. 当构造抬升，侵蚀基准下降，始准平原上面的河流，从河口开始逐渐下切，开始进入幼年期，如图2中曲线1所示. 而尚未被侵蚀到的河段，仍处于均衡状态. 河口段不断下切，形成溯源侵蚀波向上游推进，使河口以上的各个河段依次进入幼年期，如图2中曲线2所示. 这一过程中，持续下切的河段，山高谷深，坡陡流急，显现出典型的高山峡谷地貌. 越向上游，进入下切期的历时越短，谷坡渐低缓，河谷渐宽展，比降减小的反常现象. 在我国，青藏高原内部平坦缓丘、宽谷、山脉、湖泊相间，周边则是高山环绕，峡谷深切. 从青藏高原发源并流出高原的河流，大都是这种类型.

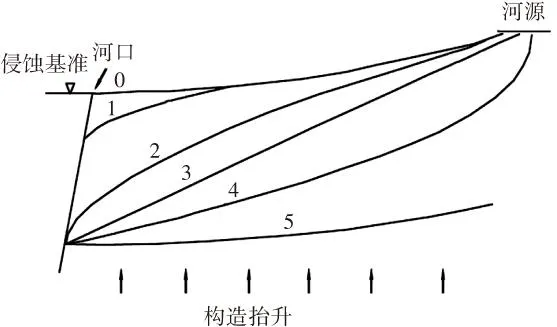
图2　大型河流的分阶段发育

若抬升停止以后，河口段停止下切. 在河口以上的河段溯源侵蚀仍继续向上游推进，直到源头后退，河谷向均一纵坡的直线型剖面发展，如图2中曲线3所示. 侵蚀基准长期稳定以后，河口段率先向壮年期和老年期进化，越向上游，进入循环的时间越短，越倾向于深切，处于幼年期，如图2中曲线4所示. 随着时间的推移，中上游段也要依次进入侧蚀盛行的壮年期和宽谷缓丘的老年期，流域地貌最终演化为准平原，如图2中曲线5所示.

2基于斯特拉勒积分和SL指标的发育阶段确定方法

本节根据斯特拉勒积分推定计算流域的发育阶段，根据SL指标判定发育阶段的分界点.

2.1确定地貌发育阶段的面积-高程分析方法

50年代美国理论地貌学家斯特拉勒提出侵蚀流域的面积-高程分析方法,可以定量地推求Davis的地貌发育阶段[14]. 面积-高程曲线(area-altitude curve)分析法是描述一定高度范围内的面积随相对高度变化所表示的曲线及其所围成的面积，相对高度可以确定侵蚀过程的强度，而残留的面积可以代表这种强度下地貌的保持能力，因此，可以说面积-高程曲线提供了地貌的发育信息[15].

记流域内等高线的值和最低点之间的高差为h，每条等高线以上的面积为a，又设全流域面积为A，流域内最高点和最低点之间的高差为H，分别以

(1)

为横坐标和纵坐标画图,得到曲线

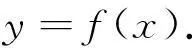
(2)

也就是面积-高程曲线，也称为斯特拉勒曲线(the Strahler’s Curve).

设定积分

(3)

上述积分即表示斯特拉勒曲线与坐标轴包围的面积，称为斯特拉勒积分(the Strahler’s integral). 可以用这个积分值推求侵蚀流域地貌演化阶段, 即

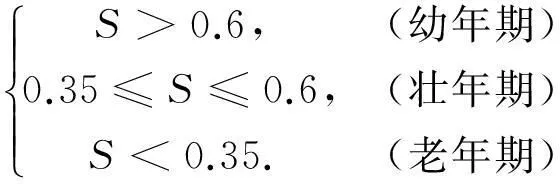
(4)

由于斯特拉勒积分为无量纲参数，因此曲线可以描述和比较不同规模的流域，但是这必须是在流域内处于同一发育阶段的前提下.

2.2确定分阶段发育的SL指标

河流的坡降指标(SL指标)经常被用来突出河流纵剖面中的坡度变化. 同时，也可以反映不同河段的抗侵蚀能力、构造运动等各种因素的差异[16]. 因此，河流的纵剖面可以清楚地反应流域地貌的演化历史. 定义k=SL或者S=kL-1, 则Hack剖面可表示为

(5)

其中：H为纵剖面的某点的高度；L为河流源头到某点的距离； C为常数；k为SL指标.

如1.2节所述，在地质构造相同、岩性均一和气候不变的条件下，河流发展到最终的均衡状态时，河床的纵剖面将呈现一个圆滑的曲线. 反应至Hack剖面中，就是从河流源头到流域出口点连成一条直线(均衡剖面)，如图3所示. 但是自然界中的河流Hack曲线都是坡折变化的. 如: 构造运动可以使整个河流发生升降或者使流域内局部地区发生变化，改变纵剖面；岩性的不同，岩石抵御侵蚀能力的差异而造成的差别侵蚀，也可以在坚硬的岩层地段形成岩槛或跌水. 这些都可以影响到Hack剖面的变化.

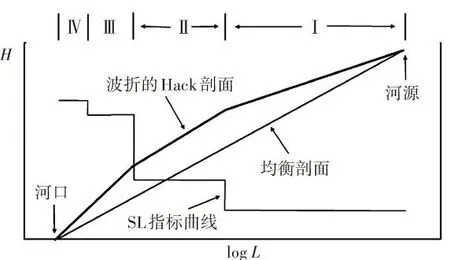
图3　河流的Hack剖面和SL指标

对于大型的山区河流，不同的发育阶段的分界点可以在Hack曲面中显现出来. 那么，可以根据Hack曲面的变化来划分同一流域中的不同发育阶段. 然后结合斯特拉勒积分，计算各个不同的发育阶段，进一步预测地震触发崩塌滑坡的灾害严重性.

3山区复杂大流域地貌发育阶段判识的案例分析

现以本世纪以来中国发生的7级以上3次大地震(玉树地震、汶川地震、芦山地震)所在的流域(通天河流域、岷江流域、青衣江流域)为例，对该理论进行验证，同时，利用这3次地震的震害现象对3个流域的发育阶段验证.

3.1流域分阶段斯特拉勒积分的计算

震区所在计算流域的斯特拉勒积分的计算步骤如下：

第1步，划定研究区域，提取研究区域的DEM. 2010年4月14日，玉树县发生Ms7.1地震,主要水系包括通天河、扎曲、巴曲等，地形以高海拔、低起伏为主. “5·12”汶川大地震和“4·20”芦山地震两次地震的主震区均属于龙门山地区，分别位于青衣江流域、岷江流域范围内,提取相应流域的DEM.

第2步，计算流域内各级分支小流域的斯特拉勒积分，绘制河流的HACK剖面. 将通天河，岷江，青衣江3条河流的流域提取，将流域的所有次级流域划分开，分别计算每个次级流域的斯特拉勒积分，如图4、5所示. 这里假设在每个次级流域内，地貌的发育阶段是相同的. 提取每条河流的纵剖面，进行数据处理得到HACK剖面和SL指标，如图6、7所示. 斯特拉勒积分可以根据HI=(Hmean-Hmin)/(Hmax-Hmin)[17]确定.

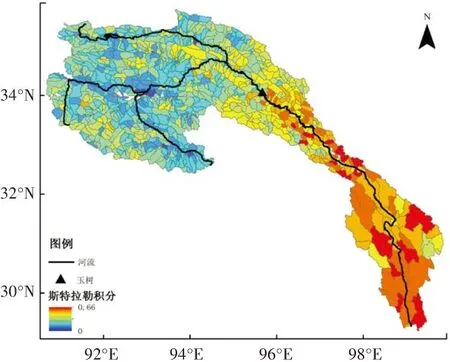
图4　通天河流域所有分支流域的HI值

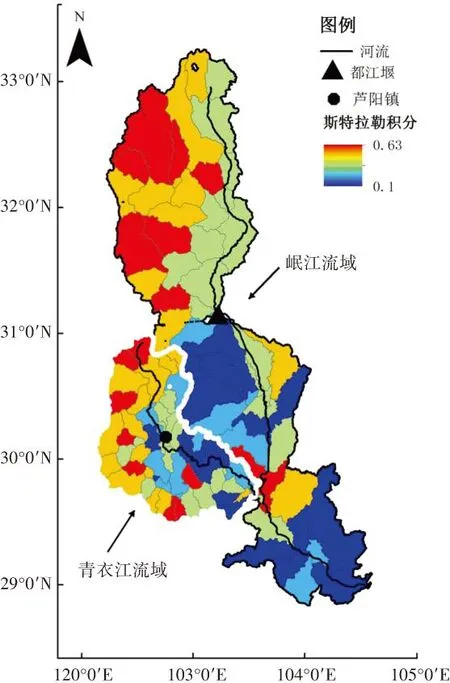
图5　岷江和青衣江流域所有分支流域的HI值

其中Hmean、Hmax、Hmin分别代表流域内高程的平均值、最大值、最小值. 目前青藏高原普遍存在着高原面、盆地面两级夷平面. 盆地面是青藏高原形成于上新世纪初至上新世纪末的第二级夷平面，盆地面内平坦开阔，切割微弱. 位于玉树以上的金沙江上游谷地是溯源侵蚀尚未达到的地方，这一地区的盆地面保存完整，较少切割；而裂点以下的金沙江河谷位于中国地形最为陡峻的横断山区，河流切割成深邃的峡谷；裂点上、下游两个地貌单元差异明显[18]. 由图4可以看出，由上游至下游，斯特拉勒积分逐渐增加，在玉树上方，斯特拉勒积分都小于0.35，属于老年期发育阶段；而在玉树下方，斯特拉勒积分逐渐增加至0.6左右，属于壮年期和幼年晚期发育阶段. 斯特拉勒积分变化趋势是与上述地貌现象吻合的.

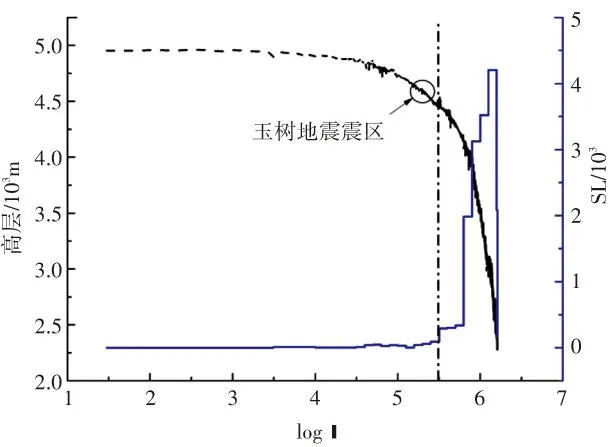
图6　通天河的Hack剖面和SL指标

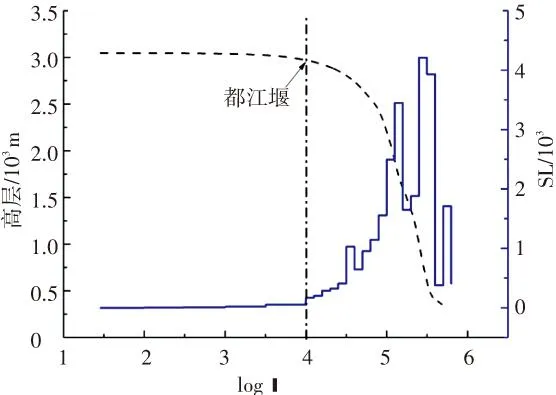
(a)岷江的Hack剖面和SL指标

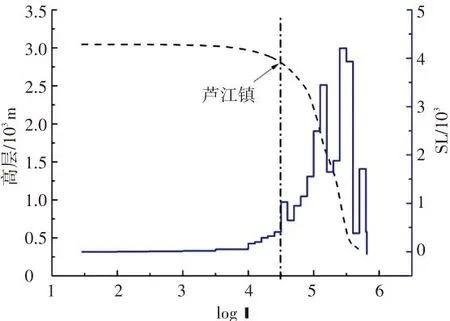
(b)青衣江的Hack剖面和SL指标

根据通天河的HACK剖面和SL指标(见图6)可以发现，SL指标的突变点在玉树处，在突变点前后，河流的SL指标突然急剧增大. 这个分界点，上述斯特拉勒积分变化的分界点，地貌现象变化的分界点，是吻合的. 青衣江与岷江同属于龙门山、岷山等一系列的山脉处于青藏高原东缘的地形陡变带中，河流走向多与龙门山垂直，以深切河谷为主要特征，进入四川盆地后河流弯转曲折，流速缓慢. 由图5可以看出，两条河流均是上游的斯特拉勒积分大，而下游的斯特拉勒积分小. 岷江以都江堰为分界点，上游的斯特拉勒积分在0.4～0.6之间，处于地貌循环的壮年期；下游的斯特拉勒积分在0.1～0.35之间(其中有一个分支小流域为0.5)，处于地貌循环的老年期. 青衣江流域以芦阳镇为分界点，上游的斯特拉勒积分在0.4～0.55之间(其中有一个分支小流域为0.35)，处于地貌循环的壮年期；下游的斯特拉勒积分在0.1～0.35之间(其中有一个分支小流域位0.5)，处于地貌循环的老年期. 岷江与青衣江的斯特拉勒积分的变化趋势与上述的地貌现象也是吻合的. 根据岷江和青衣江的HACK剖面和SL指标(见图7)，SL指标的突变点分别为都江堰和芦阳镇，这与斯特拉勒积分变化的分界点，地貌现象变化的分界点也是吻合的.

分支小流域的斯特拉勒积分的变化点，SL指标的突变点都可以作为发育阶段的分界点. 而在相同的地貌发育阶段内，斯特拉勒积分的变化并不大. 因此，本文根据SL指标的变化来划分河流的发育阶段，用发育阶段的的斯特拉勒积分代表这个发育阶段的斯特拉勒平均值.

第3步，绘制斯特拉勒曲线，计算斯特拉勒积分. 分别以玉树、都江堰、芦阳镇为通天河、岷江、青衣江流域的分界点，直接计算分界点以上的流域的整体的Strahler积分，分别为0.34、0.52、0.46，如图8 所示.

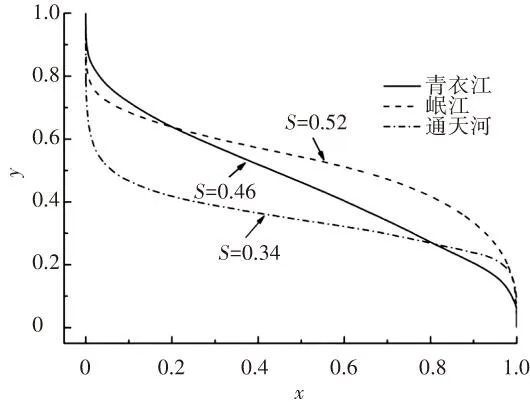
图8　青衣江、通天河、岷江流域的斯特拉勒曲线及积分

3.2计算结果与实震坡体资料对比

3.3.1芦山地震崩塌滑坡概况

芦山地震震中位于北纬30.3°、东经103°，震源深度约13 km，主震区沿龙门山断裂带分布，呈东北—西南走向，南起凉山州甘洛县，往东北经汉源、荥经、芦山至大邑县，主要位于雅安市境内,震中烈度达Ⅸ度.

利用震后遥感影像资料进行人工目视解译是大面积获取震区崩塌滑坡信息的主要方法. 芦山地震后的半年时间里，通过多种途径收集了震区航空、航天遥感影像资料，包括：1)中科院遥感与数字地球研究所提供的3批航空遥感数据，覆盖芦山、宝兴、邛崃等县市约5 000 km2. 第1批航片获取时间为2013年4月20日10:30—12:40时，分辨率为0.6 m；第2批航片获取时间为4月20日15:00—17：00时，包括0.4 m和2 m两种分辨率；第3批航片获取时间为4月21日上午，包括0.4 m和2 m两种分辨率. 2)四川省测绘地理信息局芦山地震信息发布平台公布的芦山震中区的航片影像资料(影像获取截止时间为4月25日，分辨率为0.5 m)；3)国家测绘局公布的龙门乡、太平镇、宝盛乡三地的航片影像资料(影像获取时间为4月20日18:28，分辨率为0.16 m)；对以上遥感影像资料进行几何纠正、融合、拼接、图像增强等数据处理，获得芦山震区的遥感覆盖面积为208 km2，覆盖整个IX度区. 由于震区植被发育较好，多为常年生灌木，根据崩塌滑坡造成地表破坏的新鲜与否，判断是否为本次地震造成的. 结合野外300余处灾害点的实地考察，最终确定灾害点1 754处，分布如图9所示.

3.3.2三场地震之间的对比

2008年发生了震级为Ms8.0的汶川地震，2013年发生了震级为Ms7.0的芦山地震，两次地震震区分别处于岷江流域和青衣江流域，Strahler积分分别为0.52和0.46，均处于壮年中期，地貌基本由陡峻的坡面组成(见图10、11)，谷坡处于临界坡状态. 谷坡具备地震触发大规模崩坍滑坡的条件；2010年发生了Ms7.1的玉树地震，玉树震区位于通天河流域，Strahler积分为0.34，处于老年期，宽谷缓丘是主要地貌(见图12)，谷坡已偏离临界坡，谷坡不具备地震触发大规模崩坍滑坡的条件.

选取Ⅸ度烈度区的崩塌滑坡密度作为比较指标(玉树、芦山地震最大烈度均为IX度). 芦山地震、汶川地震和玉树地震在Ⅸ度烈度区崩塌滑坡密度分别为2.5、1.0～1.5[2]、0.4[19]个/km2，可知，芦山地震、汶川地震均触发了大量的崩坍滑坡，而玉树地震次生灾害相对弱得多. 这与芦山地震、汶川地震震区具备地震触发大规模崩坍滑坡的条件，而玉树地震震区不具备此条件的评判结论是吻合的.

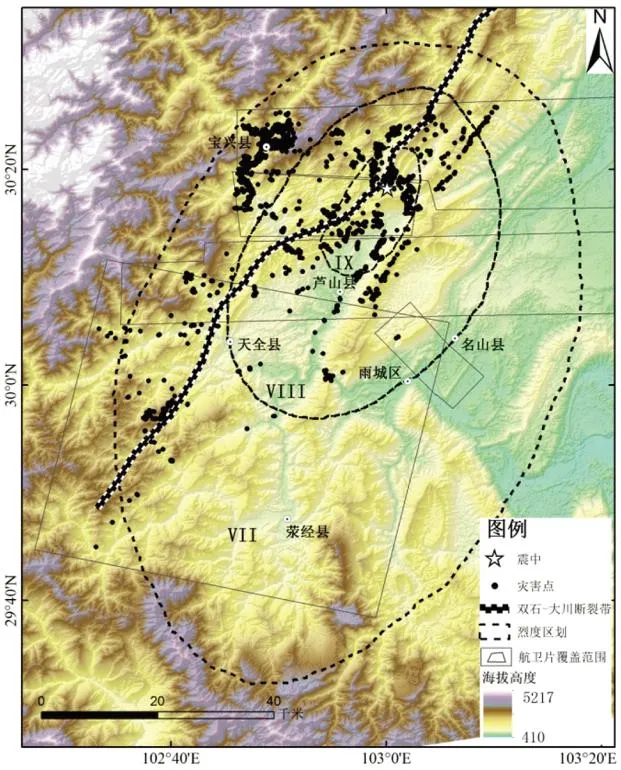
图9　芦山地震滑坡空间分布区域

图10　5·12汶川大地震岷江左岸(Ⅸ度区)山体崩塌

图11　“4·20”庐山地震IX度区宝盛乡山体崩塌

图12　玉树震区(N33°03′18.6″，E96°51′15.2″) 地貌状态[19]

4结论

1)基于地貌循环理论和山区复杂大型流域的分阶段发育的理论，将斯特拉勒积分的计算方法与SL指标结合，确定山区复杂大流域的发育阶段. 并根据发育阶段评价崩塌滑坡在降雨、地震等触发条件具备时的区域严重性. 所提出的方法亦可为其他诱因的区域性山地灾害危险性预测提供借鉴.

2)高地震烈度山区的铁路选线，是在节省工程投资和减轻未来地震灾害风险的矛盾中起着统筹规划作用的多目标决策过程，线路原则方案的选择是风险调控的首要环节. 在交通部门，对于新建线路，对预测地震触发崩塌滑坡灾势严重的路段，可通过隧道穿越方案与大范围绕避方案的经济技术比较，选择合理方案. 对于既有线路，一般采用工程措施治理降雨滑坡灾害点；但对于地震触发崩塌滑坡，由于其低频大灾的特点，大范围地修建防护工程是不现实的，建议先采取安装地震警报仪等非工程措施，控制人员车辆损失的风险.

参考文献

[1] 中国地质环境监测院.中国典型县(市)地质灾害易发程度分布图集：西南地区卷[M]. 北京: 科学出版社,2011:122-132.

[2] 黄润秋.汶川地震地质灾害研究[M]. 北京:科学出版社, 2009: 203-254.

[3] KEEPER D K.Landslides caused by earthquakes [J]. Geological Society of America Bulletin，1984, 95 (4): 406-421.

[5] 乔建平，蒲晓虹. 川西南滇北接壤带地震滑坡概述[J]. 山地研究，1987(3): 181-186.

[6] 王余庆，辛鸿博，高艳平，等. 预测岩土边坡地震崩滑的综合指标法研究[J]. 岩土工程学报，2001, 23(3): 311-314.

[7] 丁彦慧，王余庆，孙进忠，等. 地震崩滑预测方法及其工程应用研究[J]. 工程地质学报，2000, 8(4): 475-480.

[8] 许冲，徐锡伟，于贵华. 玉树地震滑坡分布调查及其特征与形成机制[J]. 地震地质, 2012, 34(1): 47-62.

[9] 许冲，戴福初，陈剑，等. 汶川Ms8.0地震重灾区次生地质灾害遥感精细解译[J]. 遥感学报，2009, 13(4): 745-762.

[10]NEWMARK N. Effects of earthquakes on dams and embankments [J]. Geotechnique，1965, 15(2): 139-160.

[11]DAVIS W M. The geographical cycle[J]. The Geographical Journal, 1899, 14(5): 481-504.

[12]蒋忠信. 滇西北三江河谷纵剖面的发育图式与演化规律[J].地理学报,1987,42(1):16-27.

[13]蒋忠信.帕隆藏布河流纵剖面演化的最小功模式[J]. 山地学报,2002,20(1):26-31.

[14]STRAHLER A N. Hypsometric (area-altitude) analysis of erosional topography [J]. Geological Society of America Bulletin，1952, 63 (11): 1117-1142.

[15]艾南山. 侵蚀流域系统的信息熵[J]. 水土保持学报,1987,1(2): 1-8.

[16]HACK J T. Stream-profile analysis and stream-gradient index[J]. Journal of Research of the US Geological Survey, 1973, 1(4): 421-429.

[17]PIKE R J, WILSON S E. Elevation-relief ratio, hypsometric integral and geomorphic area-altitude analysis [J].Geological Society of America Bulletin, 1971, 82: 1079-1084.

[18]中国科学院青藏高原综合科学考察队.西藏地貌[M].北京: 科学出版社, 1983:30-31, 200-210.

[19]中国地震局地震现场应急工作队.玉树7.1级地震断层地表破裂带和地质灾害调查报[R/OL]. (2010-04-26)[2014-12-25]. http://www.mlr.gov.cn/tdzt/zdxc/qt/ysdz/dzzl/201004/t20100426_146692.htm.

(编辑魏希柱)

Tendency prediction of collapse-landslide caused by earthquake based on the erosion cycle theory

DUAN Shusu1, YAO Lingkan1,2,3, GUO Chenwen1

(1. School of Civil Engineering, Southwest Jiaotong University, 610031 Chengdu, China; 2. Road and Railway Engineering Research Institute, Sichuan Key Laboratory of Seismic Engineering and Technology, 610031 Chengdu, China;3.MOE Key Laboratory of High-speed Railway Engineering，610031 Chengdu, China)

Abstract:A method of determining the stage of geomorphic development is built up in complicated mountainous river basin, which can also be used to regional assessment of the regional severity of collapse-landslide caused by earthquake or heavy rainstorm. Based on the theory of the erosion cycle and the theory of river’s developing by stages, the stage of geomorphic development is estimated by combining the Strahler’s integral (HI) and the stream-gradient indices (SL indices). Then regional severity of collapse-landslide is estimated by development stage with DEM (digital elevation model) and ArcGIS technique. Both of the change point of HI of branch basins and the breakpoint of SL indices can be the cut-off point of development stage. In the same development stage, HIs are very similar. HI of the whole same development stage can be the representative HI of all the HIs of branch basins. The basins in development stage of late youth and maturity have the severest regional disasters, with HI change from 0.45～0.6.

Keywords:erosion cycle theory; theory of river basin development by stage; Strahler’s integral (HI)； stream-gradient indices (SL indices)；collapse-landslide caused by earthquake

中图分类号:U211.9

文献标志码:A

文章编号:0367-6234(2016)03-0147-07

通信作者:姚令侃，yaolk@swjtu.edu.cn.

作者简介:段书苏(1988—)，女，博士研究生;

基金项目:国家自然科学基金面上项目(41172321)；

收稿日期:2004-11-11.

doi：10.11918/j.issn.0367-6234.2016.03.025

国家自然科学基金重点项目(41030742)；

中国铁路总公司科技研究开发计划课题(2013G014-A).

姚令侃(1953—)，男，教授, 博士生导师.