多商品流三层供应链网络均衡模型构建

赵国甫

内容摘要：本文研究的供应链网络均衡模型考虑了风险管理因素，可以有效降低风险损失，提高竞争优势。该供应链由生产商、零售商、需求市场的三层结构组成，分析了损失函数表达供应链中的中断风险特征及生产商、零售商、需求市场的行为优化条件，最终形成了基于风险发生概率的动态供应链网络均衡不等式模型，并采用修正投影方法求解不等式。本文通过电动车厂商案例，阐述了厂商的趋近均衡解过程。

关键词：三层供应链网络均衡模型 变分不等式 修正投影法

供应链管理被称为“企业第三利润源”，企业作为一个核心，通过与制造商、零售商、物流公司等相关部门的合作，构建供应链，并对供应链进行管理。随着全球竞争越来越激烈，企业的供应链管理成为企业界的关注热点，成为学术界的研究热点。因此探究怎样提高供应链的整体效率、怎样构建供应链结构以及对供应链内部成员之间的竞争进行协调和探究供应链的均衡，显得尤为必要。

文献综述

关于供应链网络变分不等式均衡模型已经取得了一定的研究成果。Nagurney通过对变分不等式技术的运用，对供应链网络成员之间的关系与决策行为进行了研究，并推出了单一商品流供应链网络模型，进而更深层次地探讨了多商品流供应链网络均衡模型，但是其研究以单一商品流动为主，现实中的多商品流动一般性更高；张宁采取多项式Logit分析方法对不同产地与不同品牌的跨区域市场模型进行研究，指出跨区域市场均衡是在已知供求区域、供求函数、区域间的运输成本函数的情况下，各区域产品供求与区域间运输达到的平衡，弹性供求下产销平衡运输问题为其本质；张宁与卢兴普对随机选择情况下的单个需求市场、一种类型、多种规格均衡模型进行了研究，但是其研究角度并非为供应链，而由多个生产商、零售商与需求市场组成的供应链网络均衡是在供给市场实现生产商竞争均衡、在需求市场实现供需平衡、在零售市场实现零售商竞争均衡；张铁柱等基于变分不等式的方法构建了确定性需求下的多商品流供应链网络均衡模型；徐兵等利用Logit模型及变分不等式方法探究了在随机产品选择下的多商品流供应链网络均衡模型等。在上述文献中，关于供应链的模型构建未涉及风险系数对供应链网络的影响。因此本文研究了基于风险系数的多商品流三层供应链网络均衡的变分不等式模型。

供应链风险管理的主要研究内容

通常情况下，风险都与不确定性相联系。供应链企业进行合作时，会有各种内生和外生不确定因素的存在。不确定性的存在会从主观层面上导致供应链中出现各种各样的风险。

风险可以这样定义：在一定的时期内，各种内外部因素的复杂性与变动性可能会给特定主体带来的利益损失变动。由这一定义可以引出供应链风险的定义：在整个供应链的上下游合作企业中，由于不确定性的合作关系变动导致供应链中部分成员企业甚至整个供应链可能面临的利益损失变动。

企业在进行供应链风险管理之时，会考察风险因素给企业绩效带来的影响，同时利用组织的哲学思想以及对待风险的态度设计出特定的战略决策，以对风险或者风险为企业带来的恶劣影响进行有效的控制，这是其风险管理的目的。这一目的的实施与实现过程如图1所示。

图1所示的供应链风险管理共有三个部分：一是供应链的描述与分析，二是供应链风险的识别与评估，三是供应链风险的处理。风险分析主要借助于供应链的绩效评估来对其运行状况及潜在风险水平予以把握；风险评估则倾向于對影响供应链风险的因素以及影响因素的作用机制进行分析；风险处理在评估结果的基础上对风险减小、分担、转移及规避的方式进行设计，主要涉及到供应链结构重组、制定新的供应链合作规范或激励约束机制等。在供应链风险来源中，外部因素也发挥了很大的作用，因此在进行供应链风险管理之时还应加强对外部环境影响的关注度。

三层供应链网络均衡模型构建分析

（一）问题概述

假设供应链由L个需求市场、J个零售商、I个生产商三层结构组成，对产品S进行生产、销售和消费，l代表需求市场，j代表零售商，i代表生产商，s代表生产商生产的产品。由于供应链中可能存在多个生产商，因此，对生产的产品进行假设，假设这些产品为完全同质产品，只存在产地和品牌差异。生产商和零售商都追求利益的最大化，不同的生产商及不同的零售商之间都属于合作竞争关系。生产商根据利润最大化目标确定不同产品的生产量和不同地区零售商的产品供给量，零售商根据利润最大化目标确定不同需求市场的产品供给数量及对每个产品订购量，供给市场均衡和零售市场均衡分别表现为I个生产商之间的竞争Nash均衡及J个零售商之间的竞争Nash均衡。

（二）生产商行为及优化条件

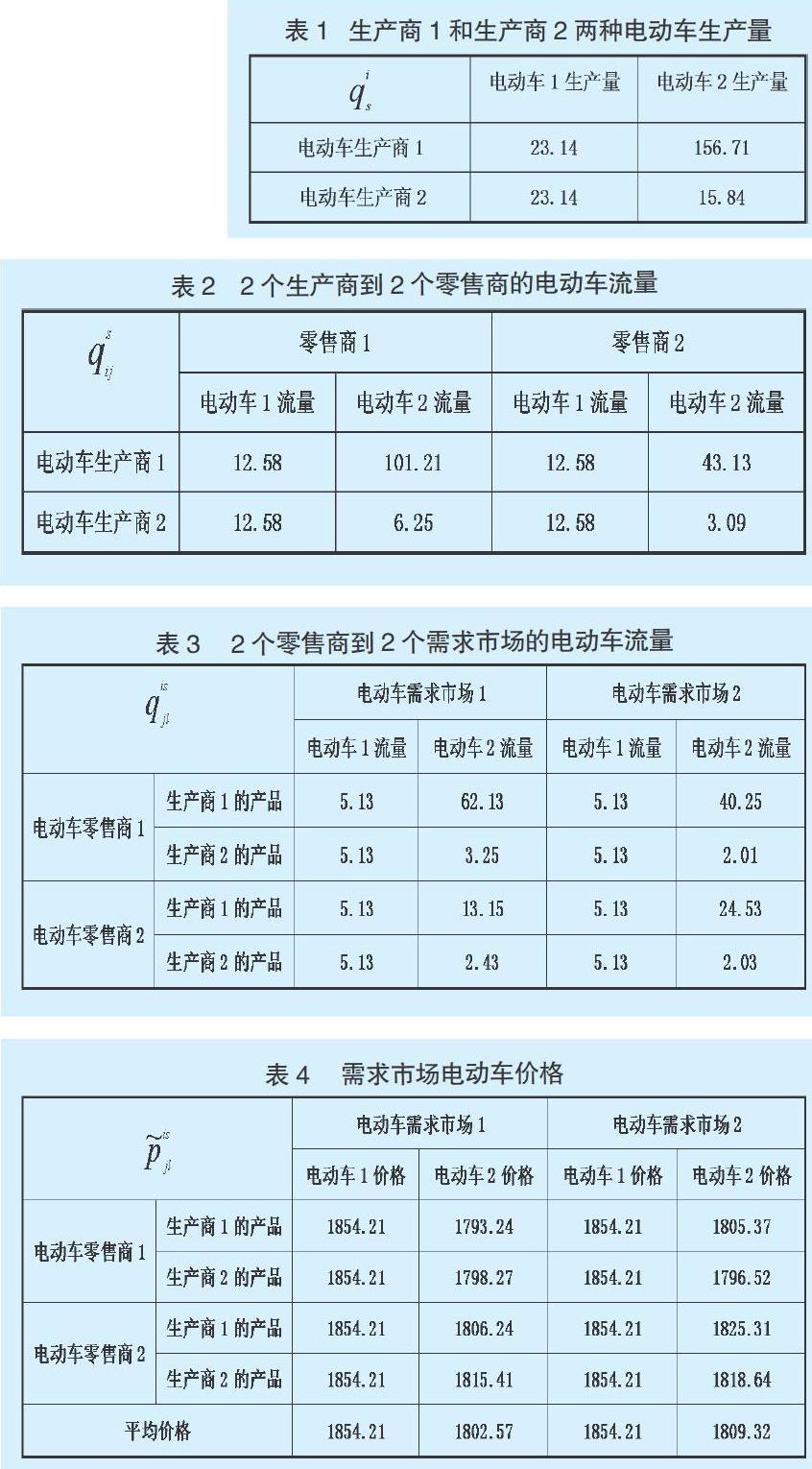
1.均衡分析。由于修正投影算法的精确度较高，本文采用Matlab7.0软件对电动车的整个销售过程进行分析，设定收敛精度ε0=0.001，步长ρ=0.01，迭代次数11次，得到的电动车供应链网络均衡结果如表1、表2、表3、表4所示。

通过表1、表2、表3、表4的分析结果可知，电动车1的供应链网络结构呈对称结构，其流量和产量达到网络均衡时呈现均匀对称分布状态，生产商1和生产商2生产的电动车1的数量相同，同一个零售商和生产商1、生产商2之间的电动车交易数量相同，2个需求市场中电动车1的价格相同，两个零售商的电动车1交易量也相同。对电动车2来说，生产商1的生产效率远远高于生产商2，电动车的生产商1和零售商1交易的边际成本比零售商2成本低，因此生产商1更倾向于和零售商1进行交易，交易量提高；需求市场1中的零售商1的电动车储存和展示边际成本比在需求市场2上的成本低，因此零售商1倾向于在需求市场1进行销售，销售量显著提高；消费者在需求市场1上购买电动车时，到零售商1处购买电动车1的单位边际交易成本低，因此消费者倾向于在零售商1处购买，提升购买量；电动车2的生产商1、零售商1、需求市场1供应链最有效，对应的电动车销售价格也最低，该供应链的电动车销量也最大。

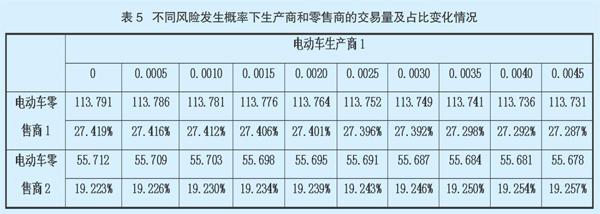
2.敏感性分析。设电动车生产商1和零售商1、零售商2发生中断风险的概率（ε0）的取值分别为0，0.0005，0.0010，0.0015，0.0020，0.0025，0.0030，0.0035，0.0040，0.0045，不同中断风险概率下，生产商与零售商之间的交易量及交易量占比发生变化，以此分析其变化的敏感性情况，结果如表5所示。

由表5可知，随着ε0的提高，电动车生产商1和零售商1之间交易量逐渐降低，其交易量占比逐步减少，而电动车生产商1和零售商2之间的运输量占比逐步加大，主要是因为生产商1和零售商1之间的交易量大，所以发生中断风险之后承担的损失也随之提高，因此为了避免过多损失，伴随ε0的提高，电动车生产商1需要调整电动车在不同零售商之间的交易量，实现整体收益最大化的目标。从整体上进行分析，节点间交易量较大的链接，随着中断风险概率的加大，需要相应减少该节点的运输量，而相应提高其他节点的运输量。

3.趋近均衡点的博弈过程分析。用修正投影方法对电动车生产商1和零售商1之间的运输量均衡过程进行分析。图2描述了生产商1和零售商1的整个运输量均衡过程。由图2可知，在初始X=0时，迭代到11次，生产商1和零售商1上的运输量基本收敛于均衡点，达到最优运输量。

结论

本文建立了基于风险管理多种商品流动三层供应链（生产商、零售商和需求市場）网络均衡变分不等式模型，并用具体算例进行求解，丰富了风险系统下的供应链管理内容。但是此供应链由于研究时间较短，还存在一定的不足之处，需要进一步进行研究。应该考虑相关经济现象及供应链网络中风险系数及风险管理方法手段，准确地对供应链网络的鲁棒性进行测评与分析。

参考文献：

1.林涛，刘文芳.服装外贸企业供应链管理模式分析[J].商业经济研究，2015（15）

2.Nagurney A，June D.Supernetworks：Decisionmaking for the information age[M].Cheltenham，England：Edward Elgar Publishing，2002

3.Nagurney A.Network economics：A variational inequality approach[M].Kluwer Academic Publishers，1993