异方差模型两阶段估计的一种新方法

崔 蕾， 张晓琴

(山西大学 数学科学学院, 山西 太原 030006)



异方差模型两阶段估计的一种新方法

崔 蕾， 张晓琴

(山西大学 数学科学学院, 山西 太原 030006)

异方差是线性回归模型中经常出现的问题, 解决异方差问题的一个常用的方法是两阶段最小二乘法.当样本容量较小时,通过分组产生重复数据,将会损失大量样本信息,使得两阶段最小二乘法得到的估计结果不具有精确性和有效性.利用正交表将样本容量扩大,并通过分组产生重复数据,进而对数据进行两阶段估计.结果表明,该方法大大降低了估计的误差,得到了更准确的拟合模型.

异方差; 两阶段最小二乘法; 分组; 正交表

0 引言

同方差性是经典线性回归模型中的一个重要假设, 它是指在回归模型中,所有的随机误差项都具有相同的方差.然而在经济、地理、医药等领域中,由于遗漏解释变量、测量误差以及随机因素的影响,大部分案例是不满足这个假设的,也就是说,模型具有异方差性[1,2].当线性模型中存在异方差时,普通最小二乘法[3]得到的估计不具有有效性,甚至不是渐进有效的,此时无法对模型参数进行显著性检验.这样,我们需要对异方差问题进行深入研究.

解决异方差的基本思路有两个:一个是变异方差为同方差[4],另一个是降低模型异方差性[5].其中加权最小二乘法[6]和原模型变换法[7]将原异方差问题转换为同方差问题解决,而模型的对数变换[8]仅仅降低了异方差的程度.对于特定的一些回归模型,原模型变换法是解决异方差问题的一个有效方法,其中随机误差项的方差估计是异方差的一个核心问题.常用的估计方法包括贝叶斯估计法[9]、极大似然估计[10]、两阶段最小二乘估计[11]等.

计量经济学中,一些无法观测的数据常常留在回归模型的误差项中,导致模型有内生的解释变量,这时两阶段最小二乘法成为一个良好的、稳健的估计方法.施三支和宋立新[12]研究了函数部分对模型的影响,首先忽略参数部分,利用部分多项式求得函数,然后根据两阶段估计,使用最小二乘法估计了参数项,并推导了参数的渐近性.欧阳志刚[13]利用两阶段最小二乘法和联立方程,首先估计国民收入、消费、投资、净出口值,并把该值作为相应的工具变量代入联立方程,其次用普通最小二乘法估计了模型参数,分析了政府支出对经济的贡献.

叶阿忠[14]于2002年提出了非参数计量经济中联立模型的局部线性两阶段最小二乘估计,并于2004[15]年对此方法进行推广,提出两阶段最小二乘变窗宽估计,他利用大数定理及中心极限定理证明了两种估计都具有渐进正态性和一致性.2006年,张荷观[11]提出了分组数据的异方差检验,并分别给出了一元及多元异方差模型的两阶段估计方法.但是,通过控制每组的样本量,会改变分组情况,不同的分组将会导出不同的参数估计和回归模型,进而使得预测误差也各不相同.特别是当样本容量较小时,分组将会损失一部分样本信息,使得回归模型精确度降低.

对于异方差,Zhang X Q等[16]提出了一个基于正交表的非参数估计方法,该方法利用正交表产生重复数据,并通过加权最小二乘法得到参数的估计.考虑到正交表是一个常用的实验设计方法,它可以将样本容量扩大,我们将对两阶段最小二乘的第一阶段进行改进,使得该方法在应对样本量较少的情况时也可以产生好的估计效果.

本文结构如下:第1节为引言,第2节介绍异方差模型中,利用混合正交表对两阶段估计法的改进,第3节从模拟和实例两方面,通过和原方法进行对比,表明改进后的方法可以降低误差,参数估计也更精确,第4节对全文进行概括和总结.

1 两阶段最小二乘改进

本节首先简单介绍张荷冠提出的两阶段估计,然后用正交表作为工具对该方法进行了一些改进.

1.1 分组数据两阶段估计

张荷冠[11]通过分组对异方差模型做了两阶段估计.对于多元线性回归模型,设(x1i,x2i,…,xpi,yi),(i=1,2,…,n)为样本数据,首先将多元线性回归模型转化为多个一元线性回归模型,并分别对每个一元线性回归模型进行异方差性检验,这里不妨设第一个自变量x1是引起模型异方差的主要因素, 然后对该数据进行下列操作:

(1)将样本数据按照自变量x1从小到大排序, 其他自变量和因变量保持原来的对应关系;

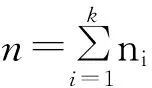
(3)假设分组数据(x1i,x2ij,…,xpij,yij)满足多元回归模型

(1)

对原模型做变换, 等式两端同除以σi,则误差项εij/σi变为同方差;

1.2 两阶段估计法的改进

当样本容量较小时, 通过分组产生重复数据会导致大量样本信息损失, 使得回归模型精确度降低. 张晓琴[16]等提出利用正交表产生重复数据的方法, 我们可以将此方法应用到分组数据中, 对两阶段估计法的第一阶段进行改进.

假设样本数据(x1i,x2i,…,xpi,yi),i=1,2,…,n满足下列回归模型:

(2)

且设x1是引起模型异方差性的主要原因,这里我们不妨设p=3,并通过正交表L9(34)产生重复数据,然后对数据分组,进行两阶段估计.具体步骤如下:

(1)根据正交表L9(34)及张晓琴[16]提出的方法,第i个样本变换后产生的重复数据记为:

(x1i,x2i,x3i)→

其中Δ=0.01;

(2)对于每个因变量的观测值yi,从正态分布N(yi,θ2)中产生9个随机数,记为yij,i=1,2,…,n,j=1,2,…,9,其中θ2=0.01,并把yij与(x1ij,x2ij,x3ij)相对应;

(3)对第i个样本产生的9个观测值(x1ij,x2ij,x3ij,yij)(j=1,2,…,9)按第一个自变量从小到大排列,其他自变量及因变量保持原对应关系,记与第i个样本相关的排序后的数据为第i组(i=1,2,…,n),并记该组中第一个自变量的组中值为x(1i),则分组后的数据记为(x(1i),x(2ij),x(3ij),y(ij));

(4)分组数据仍满足多元回归模型(2), 对模型进行变换, 得同方差模型

(3)

2 模拟与实例

2.1 随机模拟

本小节将通过模拟数据, 将改进后的方法和两阶段估计法进行比较. 假设回归方程为:

yi=0.2+1·x1i+1·x2i+1·x3i+εi,

i=1,2,…,n.

(4)

表1 均匀分布两阶段估计法与 改进后方法误差比较

表2 正态分布两阶段估计法与 改进后方法误差比较

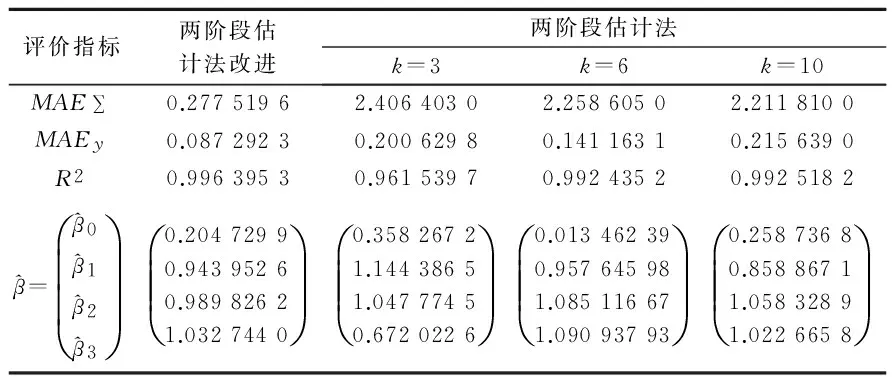
表3 指数分布两阶段估计法与 改进后方法误差比较

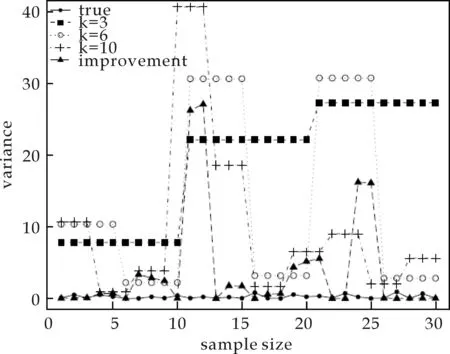
(a)均匀分布U(0,10)

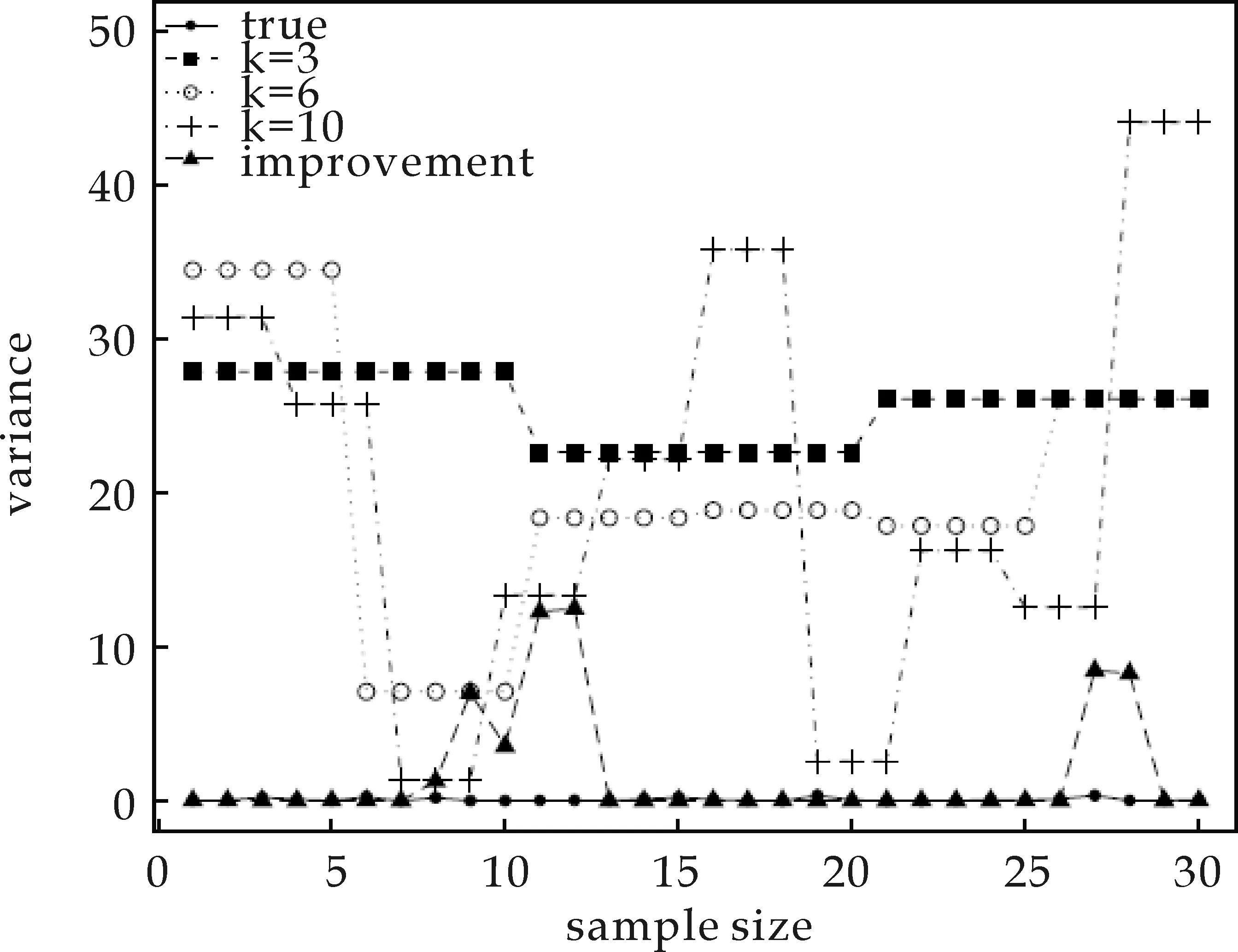
(b)正态分布N(0,10)

(c)指数分布Exp(1)图1 随机误差项方差实际值与 两方法估计值比较

图1中三条阶梯形虚线“k=3”,“k=6”和“k=10”表示的是不同分组时两阶段法得到的方差估计,“improvement”代表的是改进后方法得到的方差估计,“true”表示的是随机误差项方差的实际值.由图1可得,改进后的方法基本与实际方差重合.因此,基于分组的两阶段法并不适用于求解随机误差项估计量,而改进后的方法不管是估计误差项方差还是因变量值,都表现出良好的适应性.

2.2 实例分析

这里仍利用文献[11]的数据,将改进后的方法和原文献的方法进行对比.由于文献中数据包括一个因变量:消费性支出,以及三个自变量:收入、食品支出和文化服务支出.因此,这里需要对这些数据进行回归分析.文献[11]已经对31个地区城镇居民家庭全年人均数据进行了检验,并得出该数据具有异方差性.故我们只列出原方法和改进后方法的参数估计,并给出相应的因变量的平均绝对误差MAEy和测定系数R2.结果如表4所示.

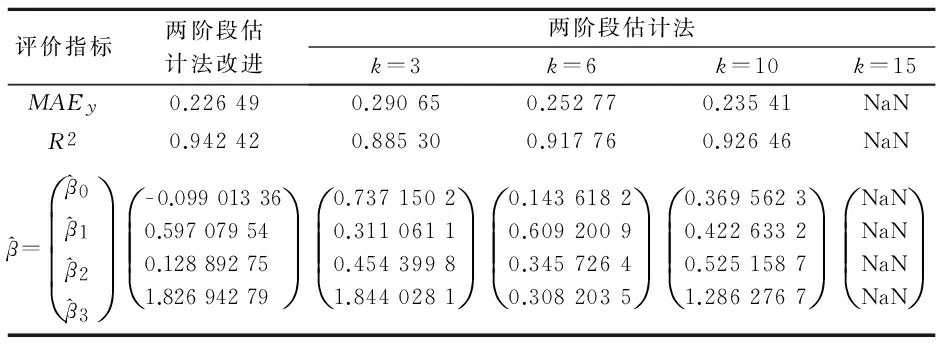
表4 城镇居民人均数据两阶段估计法与 改进后方法误差比较

3 结论

经济学中,由于样本的测量误差会随着时间的推移而不断改变,地区间抽样技术的先进程度也各不相同.因此,常常导致回归模型中随机误差项具有异方差性.而两阶段最小二乘法是计量经济学中常用的异方差估计方法,该方法需要重复数据进行估计,对样本分组是产生重复数据的一种方法.然而,不同的分组方法将导致两阶段估计法得到的估计结果各不相同.特别是样本容量较少时,组数过少将导致样本信息大量损失,组数过多,每组的样本个数降低,导致两阶段估计法不具有有效性.而本文中改进的方法通过正交表将每个样本数据扩大为一组,然后再进行两阶段估计避免了该情况的发生.

通过模拟数据和实例分析,结果表明:不管从平均绝对误差还是拟合的测定系数来看,改进后的两阶段法可以得到更优的参数估计和拟合模型,比原方法更精确,更有效.

尽管改进后的方法在估计随机误差项的方差以及模型系数中都表现出良好的适应性.但由于利用正交表扩大自变量样本后,因变量的产生具有随机性,这会影响误差项方差的估计,进而使模型拟合精度降低.且对于扩大后的每组样本,用第一个因变量的组中值代替本组中所有该因变量的观测值,也并不是完全合理的.因此在今后的研究中,我们需要从这两方面作进一步探索.

[1] Pelenis,Justinas.Bayesian regression with heteroscedastic error density and parametric mean function[J].Journal of Econometrics,2014,178(3):624-638.

[2] Cao C Z,Lin J G,Zhu X X.On estimation of a heteroscedastic measurement error model under heavy-tailed distributions[J].Computational Statistics & Data Analysis,2012,56(2):438-448.

[3] 李子奈,潘文卿.计量经济学[M].北京:高等教育出版社,2000.

[4] Kwanho C,In Kwon Y,Richard A,et al.Asymptotic theory for Box-Cox transformations in linear models[J].Statistics & Probability Letters,2000,51(4):337-343.

[5] 王红瑞,林 欣,钱龙霞,等.基于异方差检验的水文过程隐含周期分析模型及其应用——Ⅱ应用[J].水利学报,2008,39(12):1 296-1 301.

[6] Wang C,Qi F,Shi G M,et al.A linear combination-based weighted least square approach for target localization with noisy range measurements[J].Signal Processing,2014,94:202-211.

[7] Feng Z H,Wang T,Zhu L X.Transformation-based estimation[J].Computational Statistics & Data Analysis,2014,78:186-205.

[8] Packard G C.Multiplicative by nature:Logarithmic transformation in allometry[J].Journal of Experimental Zoology,2014,332(4):202-207.

[9] 鄢伟安,宋保维,段桂林,等.威布尔部件的经验贝叶斯评估[J].系统工程理论与实践,2013,33(11):2 980-2 985.

[10] Fortin M,Daigle G,Ung C H,et al.A variance-covariance structure to take into account repeated measurements and heteroscedasticity in growth modeling[J].European Journal of Forest Research,2007,126(4):573-585.

[11] 张荷观.基于分组的异方差检验和两阶段估计[J].数量经济技术经济研究,2006,23(1):129-137.

[12] 施三支,宋立新.部分线性回归模型中的广义似然比检验[J].吉林大学学报(理学版),2007,45(1):56-62.

[13] 欧阳志刚.我国政府支出对经济增长贡献的经验研究[J].数量经济技术经济研究, 2004,21(5):5-10.

[14] 叶阿忠.非参数计量经济联立模型的局部线性两阶段最小二乘估计[J].运筹与管理,2002,11(5):19-23.

[15] 叶阿忠.非参数计量经济联立模型的局部线性两阶段最小二乘变窗宽估计[J].数学的实践与认识,2004,34(1):13-18.

[16] Zhang X Q,Hao H X,Liang J Y.A new nonparametric estimation method of the variance in a heteroskedastic model[J].Hacettepe University Bulletin of Natural Sciences & Engineering,2015,44(1):239-245.

【责任编辑：陈 佳】

陕西科技大学5项科技成果荣获陕西省2015年度科学技术奖

2016年9月22日，陕西省科技创新大会在西安召开，陕西科技大学5项科技成果荣获陕西省2015年度科学技术奖.陕西省委书记娄勤俭、省长胡和平、副省长张道宏等领导出席会议并讲话，陕西科技大学校长姚书志参加了会议.陕西科技大学独立主持完成的4项科技成果荣获陕西省科学技术奖二等奖，与他人合作完成的1项成果荣获陕西省科学技术奖三等奖.具体获奖科技成果如下：

张美云、李金宝、蒋学、徐永建、修慧娟、马兴元、曹力君、贺行、张向荣完成的“基于高性能微晶纤维素制备的麦草高值利用技术与应用” 科研成果获得陕西省科学技术奖二等奖；汤伟、董继先、王博、王樨、赵延惠、刘权茂、董超、李虎完成的“中高速卫生纸机全集成自动化控制系统”科研成果获得陕西省科学技术奖二等奖；张安龙、王森、罗清、杜飞、景立明、任建华、王猛、郝建昌完成的“高效厌氧好氧二级生化加芬顿氧化技术用于有机废水处理的技术推广” 科研成果获得陕西省科学技术奖二等奖；曹丽云、欧阳海波、李嘉胤、许占位、孔新刚、介燕妮、卢靖、费杰、李翠艳完成的“锂离子电池材料湿化学合成研究及应用”科研成果获得陕西省科学技术奖二等奖；陕西咸阳宇迪电子有限公司与陕西科技大学张方辉、范应娟、孙立蓉、张麦丽、牟强合作完成“高性能LED线光源技术研究”科研成果获得陕西省科学技术奖三等奖.

陕西省科学技术奖是陕西省人民政府设立的省级最高科技奖，每年评选一次，以表彰奖励在科学技术进步活动中做出突出贡献的科技工作者.与以往不同，2016年大会首次颁发了陕西省基础研究重大贡献奖，奖金为80万元，专门用于奖励为基础研究做出重大贡献的卓越人士，旨在进一步调动全省基础研究科研人员的积极性和创造性，持续增强陕西基础研究领域的竞争能力.2015年度，陕西全省共有256项成果获得陕西省科学技术奖.其中，一等奖36项、二等奖109项、三等奖111项.

A new method of two-stage estimation about heteroscedastic model

CUI Lei, ZHANG Xiao-qin

(School of Mathematics Science, Shanxi University, Taiyuan 030006, China)

Heteroscedasticity is a problem that often appears in the linear regression model,two-stage least squares method is a common method to solve this problem.When the sample size is small,grouping the samples to produce repeated data will lose a lot of information,and this will lead to the loss of accuracy and effectiveness for the estimation of two-stage least squares method.In this paper,we will expand further samples using orthogonal array,and grouping them to obtain repeated data,finally we can get the estimate by two-stage estimation.Results show that this method will reduce the error of estimation,and get a more accurate fitting model.

heteroscedastic; two-stage least squares method; grouping; orthogonal array

图1 陕西科技大学田径场 图2 陕西科技大学实验楼群

2016-06-24

山西省自然科学基金项目(2015011044)； 山西省国际合作与交流项目(2015081020)； 山西省高等学校教学改革项目(J2014006)

崔 蕾(1991-)，女，山西晋城人，在读硕士研究生，研究方向：异方差模型

1000-5811(2016)05-0179-05

O212.1

A