数控加工中NURBS曲线的小线段离散方法

李建刚，孙喜庆，王　琳，郑德鹏

(1．哈尔滨工业大学深圳研究生院，518055深圳; 2．上海大屯能源股份有限公司选煤中心，221611江苏徐州)



数控加工中NURBS曲线的小线段离散方法

李建刚1，孙喜庆1，王琳2，郑德鹏1

(1．哈尔滨工业大学深圳研究生院，518055深圳; 2．上海大屯能源股份有限公司选煤中心，221611江苏徐州)

摘要:针对将NURBS曲线离散成连续小线段轨迹问题，提出局部等弦长、等弦差、偏转角可控的离散算法．分别对等弦长、等弦差离散算法进行仿真，验证这两种算法的优缺点;结合弦长、弦差和偏转角之间的耦合关系，提出对NURBS曲线进行区域分割，实现离散后的小线段轨迹局部等弦长、等弦差，轨迹相对光顺．利用平面光栅进行实验验证，实验结果表明:利用该算法，离散后的小线段轨迹可以很好地逼近原NURBS曲线，并且保证轨迹相对光顺．

关键词:NURBS曲线;离散算法;连续小线段轨迹;等弦长;等弦差

目前，多数CAD/CAM系统是采用NURBS参数曲线曲面形式来表达复杂的零件表面，如汽车模型、飞行器模型、涡轮叶片等［1－2］．加工曲面的轨迹有两种输出形式:

第一种是针对传统的CNC机床只能实现直线插补和圆弧插补，CAM必须根据各种设定误差，将NURBS曲线离散成小线段，用连续小线段轨迹近似NURBS曲线．针对参数曲线的离散方式主要有等弦长和等弦差两种方法．等弦长离散是保证离散后的小线段长度近似相等［3－4］;等弦差法是指离散后的小线段相对于原曲线弦差近似保持不变［5］．但上述两种离散算法主要针对曲线离散的弦差和计算的快速性方面进行研究，并没有考虑离散后的小线段轨迹中的线段长度、段间夹角等对数控系统中的插补、速度规划以及控制的影响，例如过长或过短的小线段轨迹容易使机床产生较大的速度波动，不利于机床的平稳运行;而如果线段间的夹角过大，则容易导致加工工件表面不够光顺．

第二种是直接输出NURBS曲线形式的刀具轨迹，这种轨迹因为没有各种近似误差，加工出的工件表面非常光滑．目前，国外许多高档的数控系统如FANUC、SIEMENS支持NURBS曲线插补方式．同时，已经有很多学者提出了NURBS曲线插补器设计的相关算法文献．但是，这些算法因为计算量较大或者支持的NURBS曲线有一定要求，很难在实际系统中被广泛采用［6－12］．

为了在不支持NURBS曲线插补器的数控机床上加工出符合要求的光滑曲面，又避免第一种轨迹带来的问题．本文提出在CAD/CAM软件中输出NURBS曲线轨迹，将NURBS曲线离散成为微小直线段的算法和后续数控加工特性相结合，在原有算法的基础上，提出对连续NURBS曲线在局部范围的等弦长、等弦差、偏转角可控的离散算法，使曲线离散后的小线段轨迹在局部是等弦长、等弦差，更有利于进行后续的数控加工，同时算法考虑了段间夹角，保证了离散后的轨迹相对光顺．

1　NURBS曲线及其离散

1．1 NURBS曲线的定义和性质

一条k次NURBS曲线可以表示为一分段有理多项式矢函数［13］．

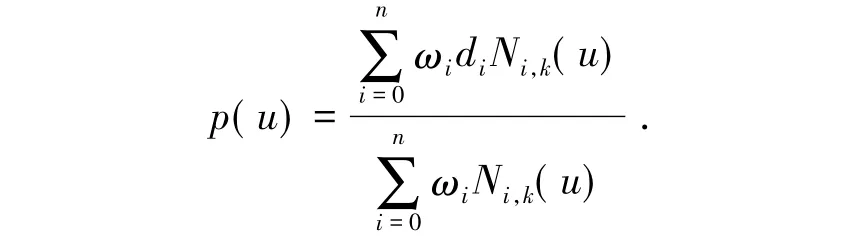
式中:ωi(i=0，1，2，…，n)称为权重因子(weights)，各自与控制点di(i=0，1，2，…，n)相关联．首末全因子ω0，ωn＞0，其余ωi≥0．且顺序k个权因子不同时为零．Ni，k(u)是由节点矢量U=［u0，u1，…，un+k+1］按照德布尔－考克斯递推公式决定的k次规范B样条基函数:

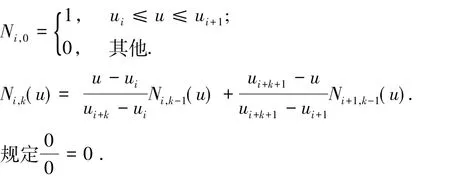
对于NURBS开曲线，常将两端节点的重复度取为k + 1，且在大多数的应用里，端节点值分别取0和1，因此，曲线定义域u∈［uk，un+1］=［0，1］．对于k次NURBS曲线上参数u∈［ui，ui+1］的一点p(u)，至多与k + 1个控制点dj及相联的权因子ωj，j=i－k，i－k + 1，…i有关，与其他的顶点及权因子无关;若移动k次NURBS曲线的一个控制顶点di或改变所联系的权因子ωi，将仅影响定义在区间［ui，ui+k+1］⊂［uk，un+1］上那部分曲线的形状，对曲线的其他部分不产生影响．

1．2 NURBS曲线离散

1．2．1等弦长离散

等弦长离散方法保证了曲线离散后小线段长度L的固定［14］．

等弦长离散有一个弊端，如图1所示，A区域曲率变化较小，应用等弦长方法可以满足离散要求; 但B、C区域曲率改变较大，应用等弦长法进行离散改变了原曲线的形状．

1．2．2等弦差离散

等弦差离散是指将曲线离散成连续小线段时，使整条曲线的弦差保持固定不变或不超过所规定的范围．在计算弦差E时，引入轮廓误差的概念，如图2所示，由于曲线线段很小，因此近似地将轮廓误差作为弦差．

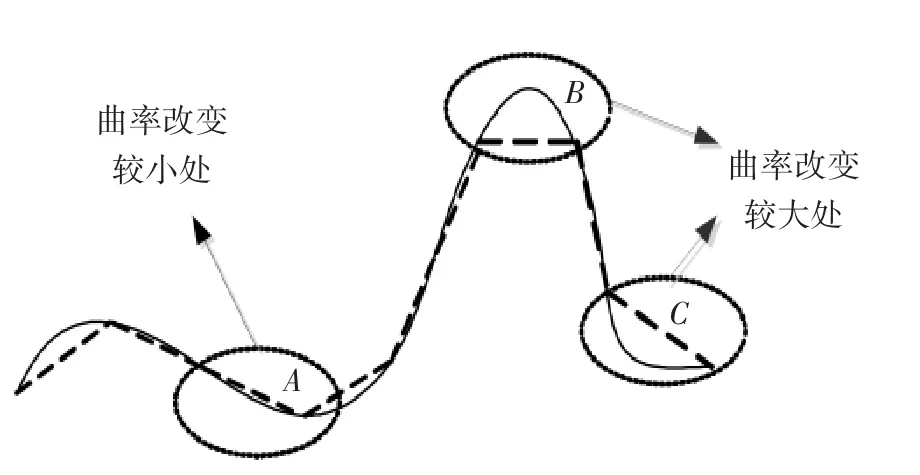
图1　曲率与等弦长离散的关系

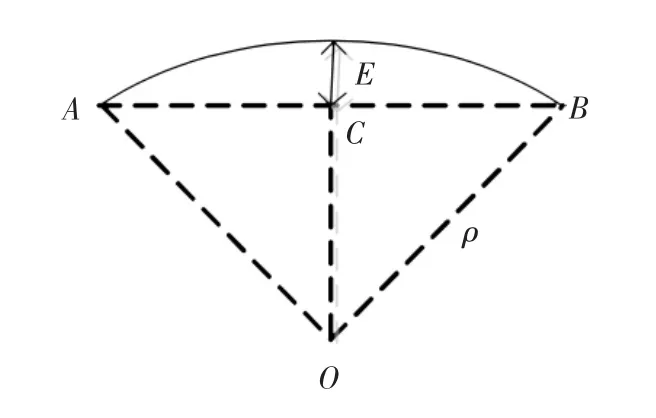
图2　轮廓误差示意

误差的计算公式如下:

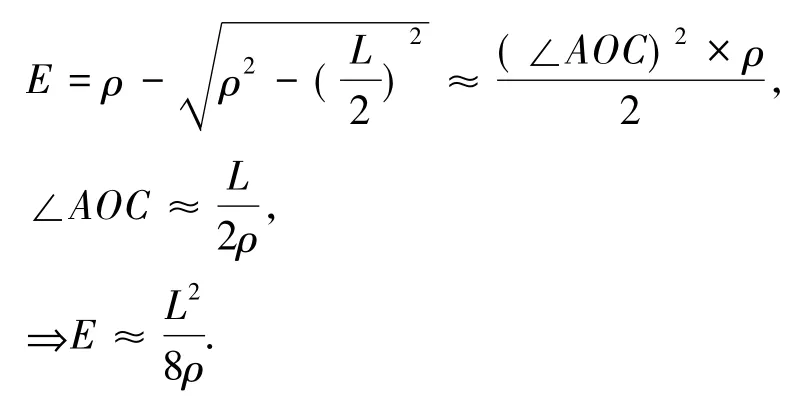
其中ρ是曲线的曲率半径．

但这种离散算法也有它的弊端，如图3所示．

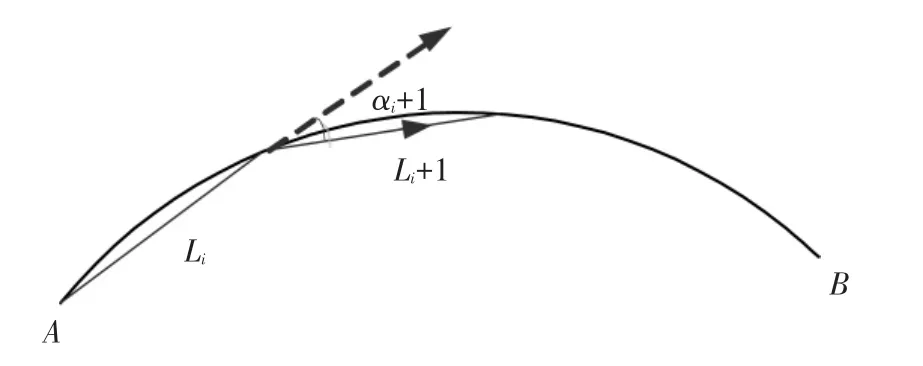
图3　偏转角定义

Li、Li+1是利用等弦差逼近曲线产生的连续小线段的长度，这里称αi是相邻连续小线段之间的偏转角．当保证弦差不变时，偏转角αi可能过大，从而造成尖角的产生．

2　局部等弦长、等弦差、偏转角可控的NURBS离散

本文的算法主要是对NURBS曲线进行局部划分，保证曲线离散后局部等弦长、等弦差、偏转角可控．图4是一条连续的NURBS曲线，在u∈［um，un］局部区间内对曲线进行离散．保证小线段轨迹弦长L1、弦差e不变、偏转角α大小可控．

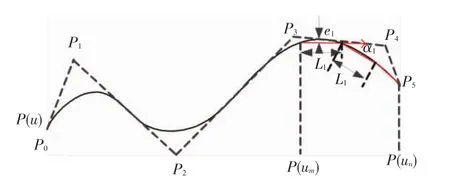
图4　局部等弦长、等弦差、偏转角可控的离散算法示意

分析弦长L、弦差e、偏角α之间的关系如下:

对于一段曲线段，当离散弦长L增大时，则离散点的数目减少，弦差e增大，前后两段的小线段偏转角α增大，离散后的连续小线段轨迹保型性降低;

当弦差e增大时，弦长L相应的增大，离散的数据点数降低，偏转角α增大，离散后轨迹保型性降低．

由以上分析可知，弦长L、弦差e、偏转角α之间有相互制约、相互耦合的关系，因此在离散时要考虑这3个变量之间的相互影响．

参考文献从［15］可知:针对曲线采用伸缩步长法进行离散时，离散前后的弦差主要受到弦长的影响，为了保证离散后的弦差不变，因此引进前后弦差比f这一参数，如图5所示．

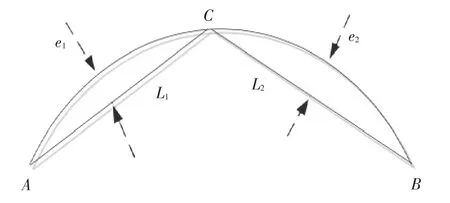
图5　前后弦差比定义

设曲线段AB为某一参数曲线上一段，被两条小线段离散，C为两小线段的交点．各段离散的弦差分别为e1、e2，弦长为L1、L2，则

设参数a，b，其中a＜1＜b．

1)当f＞b时，则L2对应的弦差较前一段弦差过大，因此缩短L2．

2)当f＜a时，则L2对应的弦差较前一段弦差过小，因此伸长L2．

3)当a＜f＜b，则前后线段弦差近似相等，弦长L2满足离散条件．

实际应用中，一般取a=0．8，b=1．2，具体视情况而定．因此，在控制离散弦长不变的前提下，检验f满足上述哪种情况就可以确定NURBS曲线的分割点;然后通过验证离散后小线段的偏转角是否满足要求，精确地定位到曲线的分割点．

离散过程如下:设变量前一段起点终点为Ps1、Pe1，后一段起点终点为Ps，Pe，前一段弦差为e1，后一段弦差为e，两段偏转角αe1e．

1)首先初始化最大离散弦长Lmax、最初离散弦长L、离散误差E、偏角α、以及弦长的伸缩步长λs，Ps=Pe=P(0)．

2)以L为弦长，计算离散的第一个数据点．判断此时的弦差e是否满足离散误差E，如果满足，转到3)．否则，缩短L，且L=L－λs，重复执行2)．

3) Ps1=Ps，Pe1=Pe，Ps=Pe，e1=e，输出Pe，记录此时L，转到4)．

4)以L为弦长，计算离散的第一个数据点．判断此时的弦差e是否满足离散误差E，如果满足，转到5)．否则，缩短L，且L=L－λe1e，重复执行4)．

5)计算此时f．

当f＞1．2，表明此段弦差较前一段弦差较大，计算出来的为区域分割点，因此缩短弦长L=L－λs，跳转至4) ;

当f＜0．8，表明此段弦差较前一段弦差较小，计算出来的该点仍为区域分割点，因此伸长弦长L=L +λs，如果弦长L≥Lmax，则令L=Lmax，跳转至4) ;

当0．8＜f＜1．2，表明此时前后两段的离散线段弦长近似相等，弦差近似相等;

进一步判断前后两段的偏转角αe1e;

如果αe1e＞α，表明此时对于该段曲线，选取的弦长过大，由于已经满足等弦长等弦差，所以，此时弦长的伸缩步长要选择小一点，为了精确的计算，这里按照L=L－0．1*λs计算，跳转4) ;

如果αe1e＜α，则表明此点满足等弦长、等弦差、偏角可控的要求．输出Pe．

6)依次循环计算至最后一点．

设3次NURBS曲线，节点矢量

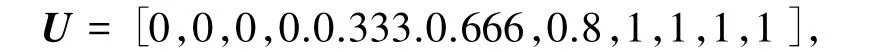
控制点{ (0，0)，(1，1)，(3，2)，(4，1)，(5，－1)，(6，－1．5)，(7，－1．9) }，权重因子均为1，设离散弦长为0．01，弦差上限为0．001，偏转角为2°．仿真结果如图6所示．

由仿真结果可以看出，经过该方法对NURBS曲线进行离散后，弦长和弦差的变化为阶梯状，即说明离散后的小线段轨迹弦长和弦差在局部范围内是近似相等的，同时离散后的轨迹偏转角在设定的范围内，说明了离散后的轨迹具有较高的光顺性;从而在离散精度和光顺度满足要求的前提下，使离散后的连续小线更有利于直接进行CNC加工．

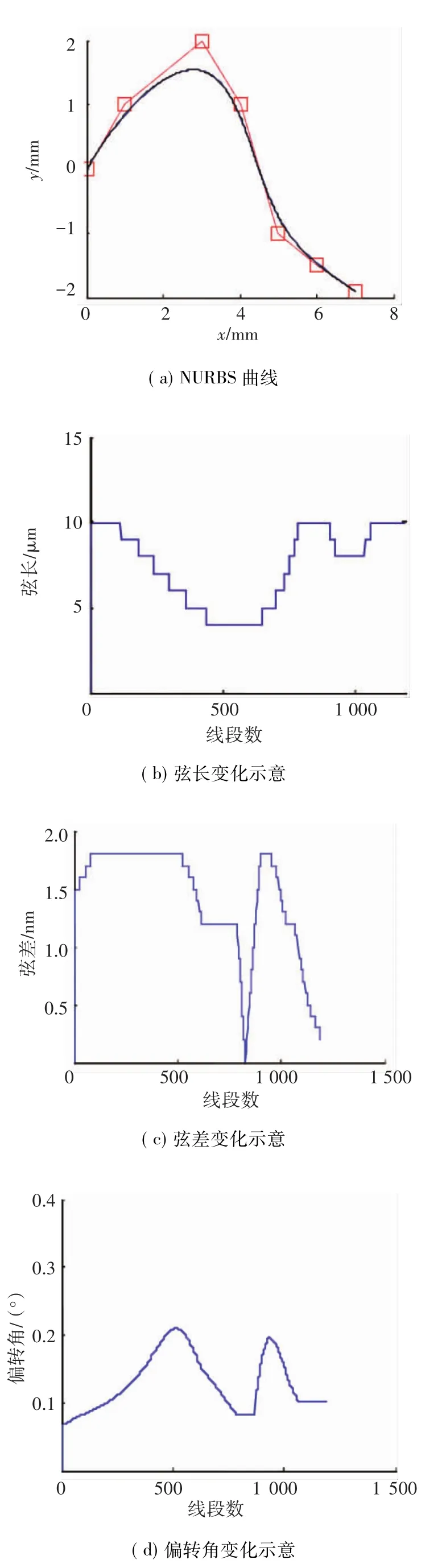
图6　NURBS曲线局部等弦长、等弦差、偏转角可控的离散仿真

3　实验验证与分析

实验主要仪器是海德汉公司生产的KMG181型号平面光栅，该仪器是一种非接触式、利用光学知识进行运动检测的装置．该仪器主要包括光栅平面、测头、机盒以及用于数据采集和分析的ACCOM软件．

实验的目的是为了验证关于NURBS曲线离散算法的可行性和优良性，并将该算法和原有的算法进行对比实验．具体实验方法如下:

1)以一条NURBS曲线为例，对曲线进行离散，分别利用等弦长、等弦差和本文提出的离散算法形成3条轨迹．

2)利用平面光栅实验仪器，测量上述3条轨迹在实际运动过程中的偏离误差，由于机床误差是一定的，不同的轨迹会产生不同的运动偏差，从而对比了不同轨迹优化算法的差别．

实验采用3次NURBS曲线，控制点p={ (0，0)，(2，5)，(8，5)，(12，0)，(8，－8)，(0，－18) (－8，－18)，(－12，0)，(－8，5)，(－2，5)，(0，0) } k=3U=［0，0，0，0，0．1，0．2，0．3，0．6，0．7，0．8，0．9，1．0，1．0，1．0，1．0］，Mat-lab绘图如图7，其曲线曲率分布如图8所示．

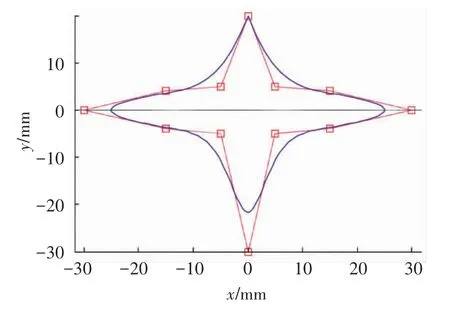
图7　实验待测NURBS曲线

图8　待测曲线曲率分布

从图8可以看出，实验所选的NURBS曲线共有3处曲率改变较大的地方，从前面的分析可知，对于曲率改变较大处，等弦长离散和等弦差离散都不能满足要求，因此该曲线具有一定的代表性，可以验证本文所提算法的优越性．将上述轨迹导入平面光栅中，启动机床．统计实验运行结果，最大轨迹偏差和速度偏差值如表1所示．

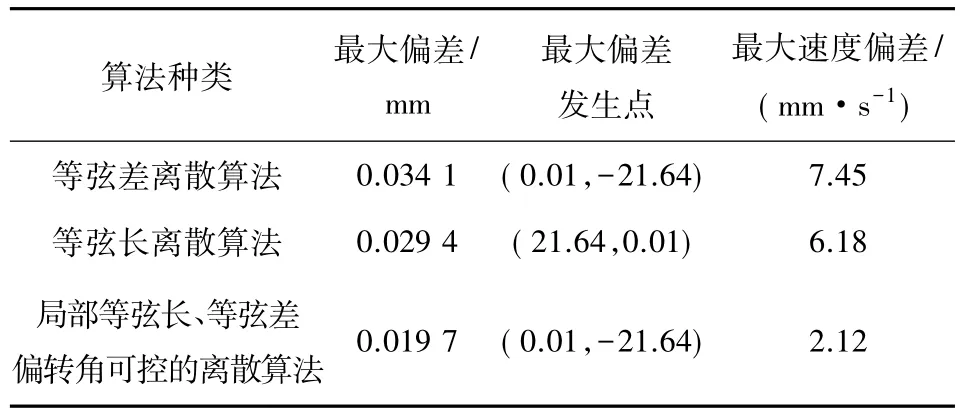
表1　轨迹运行状态表

从以上实验结果可以看出，等弦差和等弦长离散算法的最大运动偏差近似相近，均是在曲率改变较大处产生最大偏差;局部等弦长、等弦差、偏转角可控的离散算法会产生较小的最大偏差，并保证轨迹在曲率较大处可以平稳的过渡．3种轨迹优化算法的最大速度偏差都不是很大，本文提出的离散算法虽然开始时会产生最大的速度偏差，但到后期会产生较平稳的速度变化，这主要是因为该算法在起初要设定初始的离散弦长，然后根据弦差和偏转角的限定因素，逐步的去调整弦长的参数，从而达到类似于自整定的过程，实现弦长、弦差和偏转角3个参数的合理配置．实验结果表明，本文所提的离散算法和拟合算法可以进行平稳的加工，因此，本文所提出的算法是可行、有效的．

4　结　论

1)分析了利用传统的曲线离散算法如等弦长或等弦差法产生的小线段轨迹在数控加工中的不足．

2)讨论了弦长、弦差和离散后的段间夹角之间相互制约的关系，在原有算法的基础上提出局部等弦长、等弦差、偏转角可控的曲线离散算法，保证离散后的轨迹更适合于数控系统的后续加工，并进行算法仿真．

3)利用平面光栅，验证本文提出的离散算法，实验结果表明，该算法避免了在曲线曲率改变较大的地方出现尖角或过大偏差的缺点，产生的轨迹相对光顺，机床运行速度相对于传统的离散算法更加平稳，证明了该离散算法更有利于CNC的加工．

［1］周杨，刘瑛．数控加工中非圆曲线离散方法的误差分析［J］．机械研究与应用，2012，25(4) : 54－56．

［2］蔡永林，孙卫青．一种新的平面曲线圆弧插补节点获取方法［J］．工程图学学报，2002，23(1) : 97－103．

［3］文豪，高健．数控系统等误差直线逼近节点算法分析与改进［J］．机械设计与制造，2013 (9) : 217－219．

［4］范云霄，郑轶．等误差直线逼近非圆曲线的节点计算及刀具轨迹模拟［J］．工具技术，2002，36(8) : 30－32．

［5］乐英，韩庆瑶，王璋奇．NURBS曲线数控加工中的一种逼近方法［J］．机床与液压，2007，35(1) : 63－64．

［6］LI J，ZHANG T，LI Z．An adaptive off-line NURBS interpolator for CNC machining［J］．The International Journal of Advanced Manufacturing Technology，2012，63 (5/6/7/8) : 719－729．

［7］LUO Fuyuan，YOU Youpeng，YIN Juan．Research on the algorithm of NURBS curve bidirectional optimization interpolation with S-type acceleration and deceleration control［J］．Journal of Mechanical Engineering，2012，48 (5) : 147－156．

［8］DU D．An accurate adaptive parametric curve interpolator for NURBS curve interpolation［J］．The International Journal of Advanced Manufacturing Technology，2007，32 (9/10) : 999－1008．

［9］LAURENT-GENGOUX P，MEKHILEF M．Optimization of a NURBS representation［J］．Computer Aided Design，1993，25(11) : 699－710．

［10］MEEK D S，WALTON D J．Approximating quadratic NURBS curves by arc splines［J］．Computer-Aided design，1993，25(6) : 371－376．

［11］任秉银，梁兆东，孔民秀．机械手空间圆弧位姿轨迹规划算法的实现［J］．哈尔滨工业大学学报，2012，44(7) : 27－31．

［12］LIU Yu，ZHAO Bo，DAI Li，et al．Feedrate system dynamics based interpolaor for NURBS curve［J］．Journal of Mechanical Engineering，2009，45 (12) : 187－191．

［13］PIEGL L，TILLER W．The NURBS Book(Monographs in Visual Communication)［M］．Berlin Heidelberg: Springer，1997．［14］边玉超．CNC系统中NURBS曲线实时插补算法研究［J］．机械制造与自动化，2003(6) : 36－39．

［15］王学颖，任鹏．数控机床等弦长拟合优化算法的实现［J］．沈阳师范大学学报(自然科学版)，2010(4) : 499－502．

(编辑杨波)

NURBS curve separation algorithm for CNC machining

LI Jiangang1，SUN Xiqing1，WANG Lin2，ZHENG Depeng1
(1．Harbin Institute of Technology Shenzhen Graduate School，518055 Shenzhen，China; 2．Shanghai Datun Energy Resources Co．，Ltd Coal preparation center，221611，Xuzhou，Jiangsu，China)

Abstract:A new method is proposed to solve the problem of NURBS curve separation．Firstly，both of the equal chord length and the equal error separation algorithms are simulated to verify the advantages and disadvantages．Given the relationships among chord length，error and deflection angle，the separation of the NURBS curve is proposed．The algorithm guarantees the chord length and error remaining unchanged，and the deflection angle stays in a feasible range．Then some simulations are carried out to test the correctness of the algorithm．At last，the plane grating is used to make an experience to verify the algorithm．Experimental results indicate that the continuous line segments can approach the NURBS curve with the proposed algorithm accurately and the fitting location is smooth．The proposed approach can discrete the NURBS curve into the continuous line segments effectively．

Keywords:NURBS curve; separation algorithm; continuous segments location; constant chord; constant error

通信作者:李建刚，jiangang_lee@ 163．com．

作者简介:李建刚(1976—)，男，教授，硕士生导师．

收稿日期:2014－12－26．

doi:10．11918/j．issn．0367-6234．2016．01．008

中图分类号:TH164

文献标志码:A

文章编号:0367－6234(2016) 01－0053－05