TATB晶体的状态方程与振动性质的密度泛函理论研究

蒋文灿， 陈 华， 张伟斌

(1. 中国工程物理研究院化工材料研究所，四川 绵阳 621999； 2. 中国工程物理研究院研究生部，四川 绵阳 621999)

1 引 言

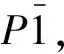
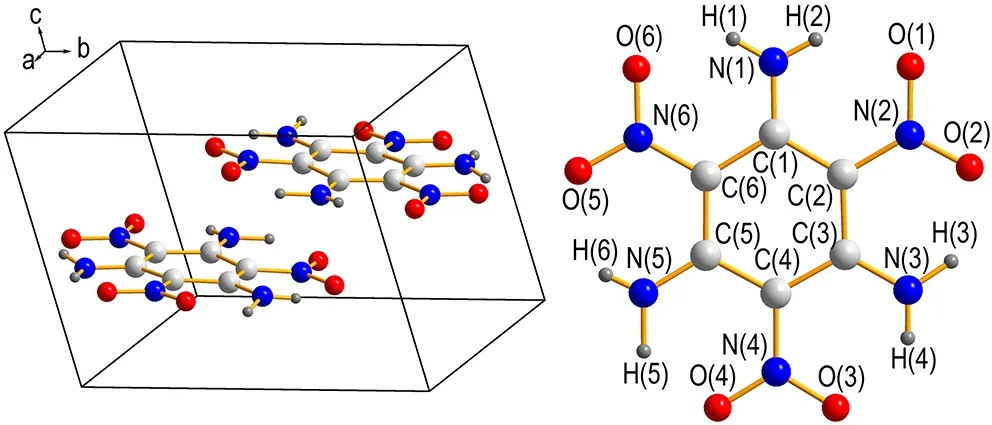
a. crystal structure b. molecule structure

图1 TATB晶体与分子结构

Fig.1 Crystal and molecule structure for TATB

2 计算方法

理论计算运用VASP软件[26]进行，初始晶体结构XRD实验数据[1]，基于广义梯度近似(GGA)的投影缀加平面波(Projector augmented wave，PAW)赝势，引入vdW-DF2修正范德华力。截断能设置为600 ev，k点取为2×2×2，截断能和k点选择保证每个原子最大受力变化不超过0.01 eV/Å，结构优化以及状态方程计算电子弛豫的标准为1×10-6eV/atom，原子弛豫标准1×10-5eV/atom，振动频率通过DFPT方法[27]计算，收敛标准进一步提高，电子弛豫标准为1×10-8eV/atom，原子最大受力不超过0.001 eV/ Å。

3 结果与讨论

3.1 TATB晶体状态方程

TATB晶体状态方程(p-V曲线)拟合考虑两种半经验状态方程，即Vinet方程[28]和三阶方程[29]，状态方程形式如下:

(1)

(2)

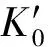
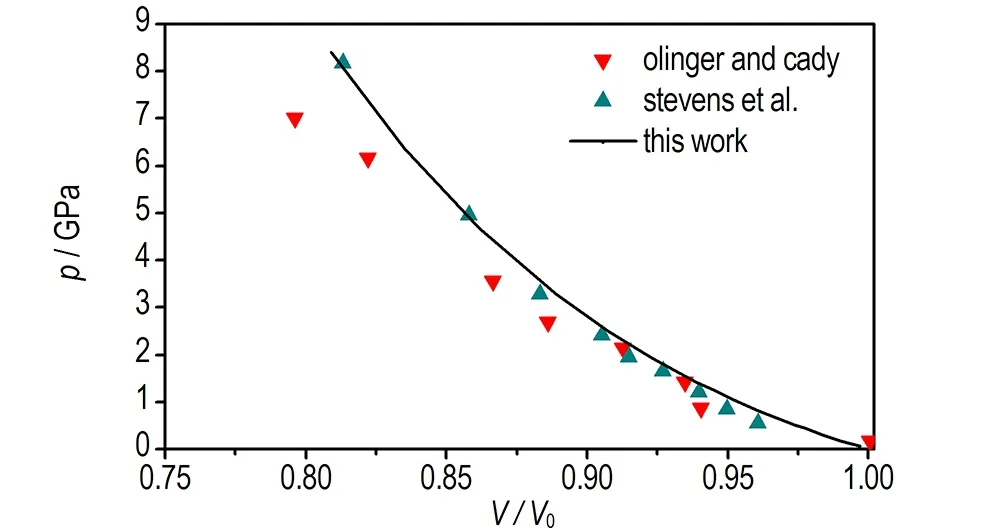
a. equation of state for TATB crystal

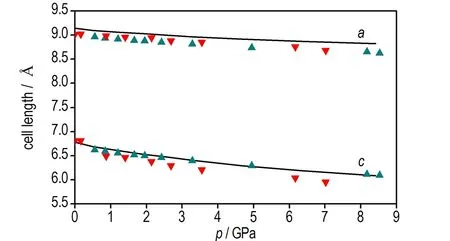
b. cell length of a axis and c axisas a function of pressure

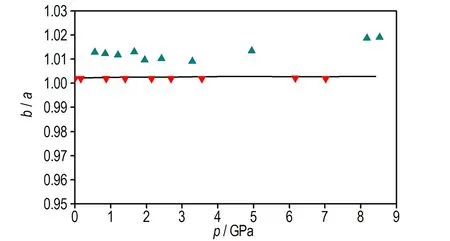
c. the ratio of cell parameters of b axisto a axis as a function of pressure

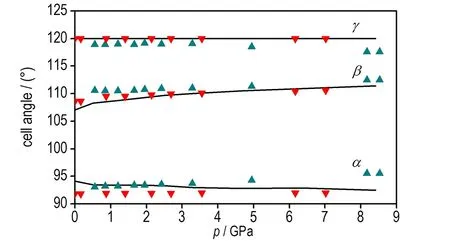
d. cell angle for α、β and γ as a function of pressure

图2 本文计算的TATB晶体状态方程以及晶胞参数与Olinger和Cady[30]以及Stevens等[4]实验数据的对比

Fig.2 Comparison of the equation of state and cell parameters for TATB determined by Olinger and Cady[30], Stevens et al[4]and calculated by this work

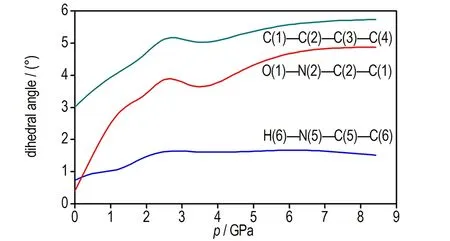
图3 TATB分子二面角随压力变化曲线

Fig.3 Dihedral angle of TATB molecular as a function of pressure

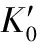
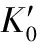
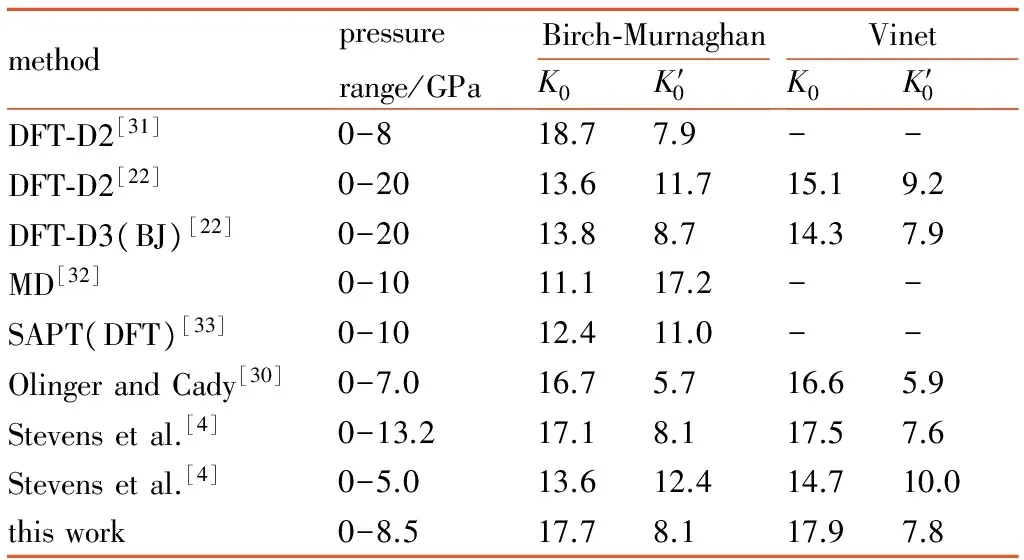
methodpressurerange/GPaBirch⁃MurnaghanK0K′0VinetK0K′0DFT⁃D2[31]0-818．77．9--DFT⁃D2[22]0-2013．611．715．19．2DFT⁃D3(BJ)[22]0-2013．88．714．37．9MD[32]0-1011．117．2--SAPT(DFT)[33]0-1012．411．0--OlingerandCady[30]0-7．016．75．716．65．9Stevensetal．[4]0-13．217．18．117．57．6Stevensetal．[4]0-5．013．612．414．710．0thiswork0-8．517．78．117．97．8

由图2d可见，加压过程中TATB晶体β和γ晶胞角几乎不变，由图2b可见c轴晶胞参数压缩性高于a轴，图2c可见a轴和b轴晶胞参数压缩率为常数，这与Olinger和Candy[30]以及其他理论计算结果[22,31]相符，表明Olinger和Candy[30]提出的两个假定是合理的。Ojede和Cagin[6]利用DFT计算结果发现加压过程在1.5 GPa附近TATB晶体内c轴方向氢键作用数明显增加，本研究统计c轴方向相邻层氢键作用数发现(截断半径2.5 Å)，8.5 GPa时氢原子与相邻层氧原子最近距离由3.040 Å变化为2.686 Å，表明氢键接触数量并没有增加。但随着压力进一步增大，c轴方向氢键作用数可能会增多。由图3可见0～8.5 GPa加压过程中苯环二面角C(1)—C(2)—C(3)—C(4)由3°变为5.7°，表明压力将会引起碳原子垂直苯环平面的扭转(即折叠)。另外，加压过程中氧二面角O(1)—N(2)—C(2)—C(1)由0.4°变为4.9°，而氢原子二面角H(6)—C(5)—N(5)—C(6)变化较小，由0.7°变化为1.5°，表明压力引起氧原子平面外扭转。在2 GPa附近二面角出现拐点，拐点出现原因有待进一步探索。以上计算结果表明，TATB在加压过程中出现了两处微结构变化，使TATB分子相互弯曲靠近。

3.2 TATB晶体振动性质

3.2.1 零压TATB晶体振动性质

TATB晶体中含有48个原子，根据群论相关知识[34]，共有144种振动模，其中72种拉曼振动模和72种红外振动模，由于红外光谱[7]能观察到的振动峰较少，而拉曼实验可以给出TATB晶体大部分振动峰[35]，且低频段普遍存在晶格振动与分子振动耦合现象，因此对振动频率高于250 cm-1的拉曼振动模式进行了分配，振动模式指认结果见附表(附表可查阅本刊网站)。表2列出了与Liu等[15]分配结果出现差异的振动模式以及下文高压振动性质研究中重点关注的振动模。分析表2发现，Q39和Q42处Liu等[15]对TATB分子指认结果分别为C—NO2伸缩振动与NO2摆动(表2中未列出)，但对TATB晶体分配结果为NO2摆动和C—NO2伸缩振动(见表2)，振动形式完全相反，而本文指认结果与Liu等[15]对Q39和Q42处TATB分子振动指认结果一致。Q50处振动模式除Liu等[15]观察到的NH2摆动以外，还出现了NO2摆动，因此振动情况更加复杂。Q65处振动模式与Liu等[15]结果完全不同，指认结果为苯环扭动。Q70处与Liu等[15]振动分配出现区别，为苯环面外变形振动，而随着振动频率进一步增加，Q72和Q74处苯环面外变形振动变弱，而NH2面外弯曲振动加强并逐渐变为主要振动形式，此计算结果与Liu等[15]不同，但与Sui等[10]红外实验对730 cm-1处振动分配结果相符(Q72)。Sui等[10]实验观察到783 cm-1附近振动主要为NO2剪切振动，Liu等[15]结果为NO2扭曲振动，而本文结果为NH2平面外弯曲振动和NO2剪切振动(Q80，Q81和Q84)，与Sui等[10]实验结果符合更好。1120 cm-1处(Q100)Sui等[10]人红外实验结果表明为C—NO2伸缩振动，本文指认结果为C—NO2伸缩振动，与Sui等[10]人实验结果相符，而Liu等[15]指认结果为NH2和NO2振动。另外，TATB晶体内振动耦合情况明显，如Q88，Q89，Q91，Q94，Q95指认结果表明，Q88和Q89在NH2摆动和NO2剪切振动基础上，可能还含有C—NO2伸缩，而随着振动频率增加，在Q91、Q94和Q95中出现了明显的C—NO2伸缩振动，而苯环伸缩振动也逐渐变得明显，逐渐变得复杂的振动耦合使振动模分配结果与Liu等[15]以及Sui等[10]实验对振动模式分配结果出现差异。如1030 cm-1处(Q94)，本文分配结果为NH2摆动、NO2剪切振动以及C—NO2伸缩振动，可能还含有苯环伸缩振动，Liu等[15]结果为NH2摆动和C—NO2伸缩振动，Sui等[10]和Town等[12]均为苯环伸缩振动。更加复杂的振动模式出现在1086～1300 cm-1之间，主要表现为苯环振动与NH2和NO2振动耦合，如Q105处振动同时包含苯环伸缩振动、NH2剪切振动、NH2摆动以及C—NO2伸缩振动， Q107处振动模式指认结果为苯环伸缩，C—NO2伸缩振动，C—NH2伸缩振动与摆动，可能还含有NO2的反对称伸缩振动，而这种复杂振动也可能是多种基频模发生费米共振引起[10]，随着外界压力增加，这种复杂的振动耦合很可能引起组分变化并导致振动峰劈裂与合并，并在加压和减压过程可能表现为不可逆变化。另外，3000～4000 cm-1振动频率与实验数据[35]相差较大(见附表)，最大偏差达到157 cm-1，而Liu等[15]DFT-GGA计算结果在3000～4000 cm-1之间与实验相比也出现了130 cm-1左右的偏差，这种偏差可能与DFT方法有关。

表2 TATB晶体部分拉曼活性模振动频率及其分配

Table 2 Part of Raman active vibration frequencies and their assignment in TATB crystal

modevibrationfrequency/cm-1Liu，etal[15]thisworkQ30291ringtwistringtwistQ36362ringdefromationringdefromationQ39381NO2rockC—NO2stretchQ42384C—NO2stretchNO2rockQ50522NH2rockNH2rock+NO2rockQ65700C—NO2stetchringtwistQ70711C—NO2torsionringdistortionQ72729C—NO2torsionNH2wagQ74753ringdistortion+NH2wagNH2wagQ76758C—NH2torsionringdistortion+NH2wagQ78791NH2wagNH2wagQ80794NH2twistNH2twist+NO2scissorQ81797C—NH2stretchNH2twist+NO2scissorQ84805NH2twistNH2twist+NO2scissorQ86817NH2twistNH2twistQ88849NH2rock+NO2scissorNH2rock+NO2scissor+C—NO2stretchQ89852NH2rock+NO2scissorNH2rock+NO2scissor+C—NO2stretchQ911000NH2rock+C—NO2stretchNH2rock+C—NO2stretch+NO2scissorQ941003NH2rock+C—NO2stretchNH2rock+C—NO2stretch+NO2scissorQ951087C—NO2stretchNH2rock+C—NO2stretch+NO2scissorQ1001120ringstretch+C—NH2stretchringstretch+C—NH2stretch+NH2scissorQ1071164ringstretchringstretch+C—NO2stretch+NH2rock+C—NH2stretch

3.2.2 加压TATB晶体振动性质

由于高压拉曼实验仅给出100～900 cm-1振动频率随压力变化结果，又因为1000～2000 cm-1振动形式比较复杂，本文分析了290～900 cm-1加压过程振动耦合情况，为了便于比较，使拉曼实验[9]观察到的振动频率数目与理论计算结果数量一致，结果如图4。对比发现，250～900 cm-1频段理论计算振动频率与实验数据符合较好。为了探究压力对TATB晶体振动频率的影响，分析了Q30、Q36、Q50、Q65和Q81处振动模式同时对250～900 cm-1频段其他振动频率处振动模式进行了指认，对0～8.5 GPa加压过程振动模式分析发现，随着压力增加，除Q39，Q42，Q86，Q76和Q78以外，其余振动频率处振动形式基本保持不变，加压过程在290～900 cm-1之间并未发现振动频率突变。对Q39和Q42振动模式分析发现，加压过程中在1.24 GPa时Q39由C—NO2伸缩振动变为NO2摆动，在8.5 GPa时，Q39变为苯环变形振动，Q42处振动模式在1.93 GPa由硝基摆动变为C—NO2伸缩振动，之后随着压力增加，振动形式不变。需要注意的是，Q39和Q42处均出现了苯环振动，但这种振动可能由NH2伸缩振动或者NO2摆动引起，也可能在Q42处和Q39处苯环与其余振动耦合在一起。Q76处在零压时为NH2面外摆动和面外弯曲振动与苯环面外扭曲振动，在1.42 GPa时苯环振动减弱，而在6.38 GPa时变为NH2面外摆动和NH2面外弯曲振动，含有NO2剪切振动，但并不明显，在8.5 GPa时NO2剪切振动变得明显。Q78处(如图5)在零压时为NH2面外摆动，但在0.5 GPa时还出现了NH2面外弯曲振动和NO2剪切振动，但并不明显，在1.24 GPa时NH2面外弯曲振动和NO2剪切振动变得明显。Q86处振动模式变化比较明显，在零压时为NO2面外弯曲振动，在4.67 GPa时为NH2面外弯曲振动和NO2剪切振动耦合。分析以上振动模式变化情况发现，随着压力增加，NH2面外弯曲振动或摆动与NO2剪切振动耦合，而对TATB分子结构分析结果表明在加压过程中相邻层分子相互弯曲靠近，表明TATB这种微结构变化导致了振动耦合，分子间氢键作用增强。

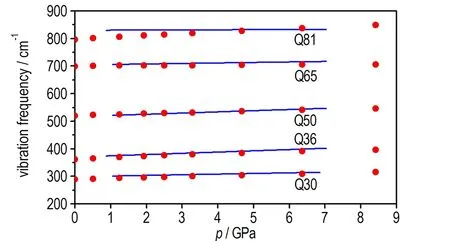
图4 加压过程中TATB晶体振动频率的计算结果(红色圆点)与实验结果[9](蓝色线)的对比

Fig.4 Comparison of the calculated values (the red dot) and the experimental ones[9](the blue line) for the vibrational frequencies under pressure process of TATB crystal

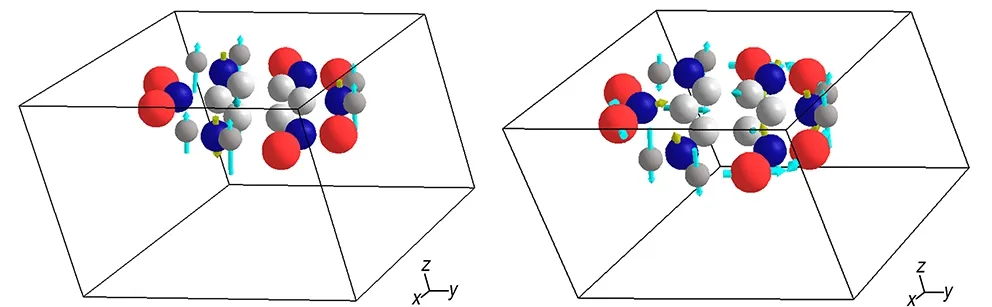
a. 0 GPa b. 8.5 GPa

图5 TATB晶体0 GPa和8.5 GPa时791 cm-1处振动模指认结果(图中红色代表氧原子，蓝色代表氮原子，白色代表氢原子，黑色代表碳原子)

Fig.5 The identification results of the vibration mode of TATB crystal at 0 GPa and 8.5 GPa at 791 cm-1. The red ball in picture represents oxygen atom. The blue ball represents nitrogen atom. The white ball represents hydrogen atom. The black ball represents carbon atom

4 结 论

利用vdW-DF2研究了TATB晶体状态方程以及振动性质，理论计算结果与实验符合较好，表明vdW-DF2能够较好地表征TATB晶体结构与性质。对状态方程研究发现，加压过程中TATB出现了两处微结构变化，即苯环折叠与硝基扭转，随着压力增加两者的变化程度增大，并在2GPa附近出现拐点。对TATB晶体部分分子内振动模式进行了重新分配，研究结果表明在1100～1500 cm-1波数之间TATB晶体振动尤其复杂，氨基与硝基和苯环振动耦合。结合理论拟合的TATB晶体状态方程，研究了压力为0～8.5 GPa，波数为290～900 cm-1，TATB晶体振动耦合情况以及分子间相互作用过程，研究发现，随着压力增加，TATB相邻层分子相互弯曲靠近，引起氨基平面外弯曲振动或摆动与硝基剪切振动耦合，表明分子间氢键作用增强。

参考文献:

[1] Cady H H, Larson A C. The crystal structure of 1, 3, 5-triamino-2, 4, 6-trinitrobenzene[J].ActaCrystallographica, 1965, 18(3): 485-496.

[2] Phillips DS, Schwarz RB, Skidmore CB, et al. Some observations on the structure of TATB[C]∥Shock compression of condensed matter-1999. AIP Publishing, 2000: 707-710.

[3] Kolb J R, Rizzo H F. Growth of 1,3,5-triamino-2,4,6-trinitrobenzene (TATB) I. Anisotropic thermal expansion[J].Propellants,Explosives,Pyrotechnics, 1979, 4(1): 10-16.

[4] Stevens L L, Velisavljevic N, Hooks D E, et al. Hydrostatic compression curve for triamino-trinitrobenzene determined to 13.0 GPa with powder X-ray diffraction[J].Propellants,Explosives,Pyrotechnics, 2008, 33(4): 286-295.

[5] Manaa M R, Fried L E. Nearly equivalent inter- and intramolecular hydrogen bonding in 1,3,5-triamino-2,4,6-trinitrobenzene at high pressure[J].TheJournalofPhysicalChemistryC, 2011, 116(3): 2116-2122.

[7] Pravica M, Yulga B, Liu Z, et al. Infrared study of 1, 3, 5-triamino-2, 4, 6-trinitrobenzene under high pressure[J].PhysicalReviewB, 2007, 76(6): 64102.

[8] Pravica M, Yulga B, Tkachev S, et al. High-pressure far-and mid-infrared study of 1, 3, 5-triamino-2, 4, 6-trinitrobenzene[J].TheJournalofPhysicalChemistryA, 2009, 113(32): 9133-9137.

[9] Davidson A J, Dias R P, Dattelbaum D M, et al. “stubborn” Triaminotrinitrobenzene: unusually high chemical stability of a molecular solid to 150 GPa[J].TheJournalofChemicalPhysics, 2011, 135(17): 174507.

[10] Sui H, Zhong F, Cheng K, et al. IR vibrational assignments for 1, 3, 5-triamine-2, 4, 6-trinitrobenzene (TATB) based on the temperature-dependent frequency shifts[J].SpectrochimicaActaPartA:MolecularandBiomolecularSpectroscopy, 2013, 114(10): 137-143.

[11] 刘红，赵纪军，龚自正，等. 原子与分子物理学报，2007, 24 (2), 291-297.

LIU Hong, ZHAO Ji-jun, GONG Zi-zheng, et al. Crystal structure of the TATB crystal under high pressure[J].JournalofAtomicandMolecualrPhysics, 2007, 24(2): 291-297.

[12] Towns TG. Vibrational spectrum of 1,3,5-triamino-2,4,6-trinitrobenzene[J].SpectrochimicaActaPartaMolecularSpectroscopy, 1983, 39(9): 801-804.

[13] Sorescu DC, Rice BM. Theoretical predictions of energetic molecular crystals at ambient and hydrostatic compression conditions using dispersion corrections to conventional density functionals (DFT-D)[J].TheJournalofPhysicalChemistryC, 2010, 114(14): 6734-6748.

[14] 刘红. 含能材料的高压行为和光谱学特性的原子模拟[D] . 四川: 西南交通大学，2006.

[15] Liu H, Zhao J, Ji G, et al. Vibrational properties of molecule and crystal of TATB: a comparative density functional study[J].PhysicsLettersA, 2006, 358(1): 63-69.

[17] Grimme S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction[J].JournalofComputationalChemistry, 2006, 27(15): 1787-1799.

[18] Lee K, Murray É D, Kong L, et al. Higher-accuracy van der waals density functional[J].PhysicalReviewB, 2010, 82(8): 81101.

[19] Grimme S, Antony J, Ehrlich S, et al. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu[J].TheJournalofChemicalPhysics, 2010, 132(15): 154104.

[20] Dion M, Rydberg H, Schröder E, et al. Van der waals density functional for general geometries[J].PhysicalReviewLetters, 2004, 92(24): 246401.

[21] Grimme S, Ehrlich S, Goerigk L. Effect of the damping function in dispersion corrected density functional theory[J].JournalofComputationalChemistry, 2011, 32(7): 1456-1465.

[22] Fedorov IA, Zhuravlev YN. Hydrostatic pressure effects on structural and electronic properties of TATB from first principles calculations[J].ChemicalPhysics, 2014, 436(7): 1-7.

[23] Shimojo F, Wu Z, Nakano A, et al. Density functional study of 1, 3, 5-trinitro-1, 3, 5-triazine molecular crystal with van der waals interactions[J].TheJournalofChemicalPhysics, 2010, 132(9): 94106.

[24] Berland K, Hyldgaard P. Analysis of van der waals density functional components: binding and corrugation of benzene and C 60 on boron nitride and graphene[J].PhysicalReviewB, 2013, 87(20): 205421.

[25] Dobson JF, Gould T. Calculation of dispersion energies[J].JPhys:CondensMatter, 2012, 24(7): 73201.

[26] Kresse G, Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set[J].PhysicalReviewB, 1996, 54(16): 11169.

[27] Baroni S, De gironcoli S, Dal corso A, et al. Phonons and related crystal properties from density-functional perturbation theory[J].ReviewsofModernPhysics, 2001, 73(2): 515.

[28] Vinet P, Ferrante J, Smith J, et al. A universal equation of state for solids[J].JournalofPhysicsC:SolidStatePhysics, 1986, 19(20): L467.

[29] Birch F. Finite elastic strain of cubic crystals[J].PhysicalReview, 1947, 71(11): 809.

[30] Olinger BW, Cady HH. Hydrostatic compression of explosives and detonation products to 10 GPa (100 Kbars) and their calculated shock compression: results for PETN, TATB, CO2, and H2O[R]. Los Alamos Scientific Lab., N. Mex.(USA), 1976.

[31] Budzevich M, Landerville A, Conroy M, et al. Hydrostatic and uniaxial compression studies of 1, 3, 5-triamino-2, 4, 6-trinitrobenzene using density functional theory with van der waals correction[J].JournalofAppliedPhysics, 2010, 107(11): 113524.

[32] 金钊, 刘建, 王丽莉, 等. 物理化学学报，2014, 30 (4): 654-661.

JIN Zhao, LIU Jian, WANG Li-li, et al. Development and validation of an all-atom force field for the energetic materials TATB, RDX and HMX[J].ActaPhysico-chimicaSinica, 2014, 30(4): 654-661.

[33] Taylor DE. Intermolecular forces and molecular dynamics simulation of 1,3,5-triamino-2,4,6-trinitrobenzene (TATB) using symmetry adapted perturbation theory[J].TheJournalofPhysicalChemistryA, 2013, 117(16): 3507-3520.

[34] 吴国祯. 分子振动光谱学[M]. 北京: 清华大学出版社，2001: 98-110.

[35] Mcgrane S, Shreve A. Temperature-dependent raman spectra of triaminotrinitrobenzene: anharmonic mode couplings in an energetic material[J].TheJournalofChemicalPhysics, 2003, 119(12): 5834-5841.