基于范例推理的边坡失稳风险评估

黄国林， 韦秉旭

(1.新疆北新路桥集团股份有限公司， 新疆 乌鲁木齐　830011；　2.长沙理工大学 交通运输工程学院， 湖南 长沙　410114)



基于范例推理的边坡失稳风险评估

黄国林1， 韦秉旭2

(1.新疆北新路桥集团股份有限公司， 新疆 乌鲁木齐830011；2.长沙理工大学 交通运输工程学院， 湖南 长沙410114)

摘要：利用已经成熟的范例推理理论对14个边坡失稳案例进行分析，并用其结果对某国道K1694+830～K1694+960段边坡的稳定性进行评估。研究结果表明：圆弧形滑坡的主要诱因是边坡过陡、岩体的不利产状、软弱夹层的力学性能差和降雨入渗导致孔隙水压力增大和岩土体的强度参数劣化，从而使岩土体更易屈服失稳；某国道K1694+830～K1694+960段边坡范例推理的滑坍风险大，建议采取必要的措施进行加固和防护。

关键词：边坡失稳； 范例推理； 风险评估； 相似度

0引言

我国国土面积大约70%为山区，是世界上滑坡比较严重的国家之一，每年因滑坡等地质灾害造成的经济损失达100～200亿元人民币。因此，滑坡的预防和治理是我国岩土工程地质领域中重大课题之一。有效地治理和预防滑坡就必须对边坡的稳定性进行科学的评价和预测。目前，对于边坡稳定性的研究主要集中在采用刚性极限平衡法和数值模拟的方法，但是这些方法一般都是针对个别案进行分析处理，并且要求建立合适的物理模型和大量的数学推导，使用者需要具有一定的力学和数值计算的基础。边坡失稳的不确定性太多、机理复杂，难以求得适合的模型，应用起来不太方便[1]。对于边坡失稳这样频繁发生的突发性事故，如何采用简单有效的方法进行科学的预测是值得研究的课题。

为此，本文利用已经成熟的范例推理理论对已有的边坡失稳案例进行统计分析，并用其结果对某国道K1694+830～K1694+960浙江开化段边坡的稳定性进行评估。

1范例推理(CBR)理论

1.1范例推理理论介绍

基于范例推理是人类推理的一种重要形式。1982年Roger Shonk在《Dynamic Memorg》中提出范例推理(Case based reasoning，CBR)的理论。此后，CBR技术广泛应用于各个领域。

在范例推理中，把需要解决的问题作为目标范例(Target case)，把已知的相似问题作为源范例(Base Case)。范例推理的基本原理就是从源范例库中挑出与目标范例最相似的范例，对源范例进行对比修正，然后对目标范例进行评估，从而得到适合的解决方案。范例推理常包括四个过程[1]： ①检索(Retrieve)，根据目标范例的信息，从源范例库中检索相似的范例集； ②重用(Reuse)，从检索到的一组相似范例中找到与目标范例相符的范例，重用该方案； ③修改(Revise)，根据修正规则对相似源范例进行修正，使之符合目标范例的条件； ④存储(Retain)，将新范例存储到范例库中，进一步完善源范例。

1.2范例推理的检索方法

范例推理的成功与否取决于目标范例与源范例的相似程度，因之相似度是检索过程的关键。

1.2.1相似度的确定

范例一般是由许多属性组成，范例间的相似度是根据属性之间的相似度定义的。通常用距离来计算相似性度，典型的有绝对值距离、欧氏距离、海明距离、切比雪夫距离和麦考斯基距离等。在此采用海明距离对边坡稳定性范例检索中的相似度进行计算，其计算公式如下：

(1)

式中：diT为目标范例T与源范例库中第i个范例之间的相似度。diT的计算结果有正有负，距离绝对值最小，则目标范例与此源范例最相似。正值表示表示目标范例比源范例边坡稳定性好；反之，负值则表示目标范例比源范例边坡稳定性差。n为范例属性总数；wh为范例属性权重值；vi(h)为范例库中第i个范例的第h个属性值；vT(h)为目标范例T的第h个属性值。

1.2.2数据归一化处理

在进行相似度计算时，不同指标因素有不同的量纲，不同参数间存在不可共度性，为防止具有较大初始值域的属性与具有较小初始值域的属性相比，权重过大，同时为了体现“奖优罚劣”[2]的原则，引入归一化效应函数，对原始数据进行归一化处理[3]。

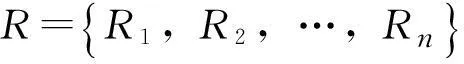
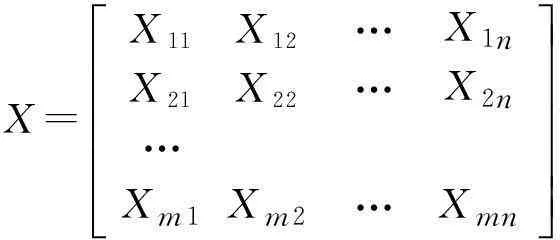
X=X11X12…X1nX21X22…X2n…Xm1Xm2…Xmnéëêêêêêùûúúúúú

(2)

对效益型指标，记中间变量Mij：

(3)

(4)

1.2.3权重值确定

因为目标范例由多个属性构成，每个属性对范例的影响程度不尽相同，常需要用权重来衡量各属性的相对影响程度。权重的评估方法较多，主要包括专家咨询法(Delphi)、主成分分析法(PCA)、特征向量法、AHP层次分析法、熵值法(Entropy)、因子分析法(Factor Analysis)和人工神经网络法等[4]。

本文用特征向量法评估权重值。具体计算方法如下：假设有n个目标范例，各有m个指标，得矩阵M：

M=X11X12…X1nX21X22…X2n…Xm1Xm2…Xmnéëêêêêêùûúúúúú

M×MT可以得到一个m阶的方正A：

A=a11a12…a1ma21a22…a2m…am1am2…amméëêêêêêùûúúúúú

则第i个指标的特征向量li为：

由归一化处理得：

2边坡稳定性分析

以往边坡稳定性研究结果表明，影响边坡稳定性的因素主要包括内因与外因两个方面。内在因素主要包括：边坡的岩土特性、岩土结构、地形地貌、地质构造、地应力场、植被条件等；外在因素主要包括：地表水与地下水相互作用、气候条件、地震情况、施工方法(爆破等)。

2.1岩土特性及结构

边坡的岩土特性及结构是影响边坡稳定的主要内因之一，不同岩土间的节理发育程度不同，所表现的力学性质及破坏机理也不相同，软硬相间，并有软化、泥化或易风化的夹层时，最易造成边坡失稳。

2.2地形地貌

深河谷地区边坡易发生松动破裂、蠕动、崩塌、滑坡等情况，前缘开阔的山坡、铁路、公路和工程建筑物的边坡等也易发生滑坡。一般来说，坡度越陡，坡高越大，对边坡稳定越不利。

2.3地质构造

地质构造关系到岩体结构面的发育程度、规模、连通性、充填程度和充填物成分，以及结构面的产状。组成斜坡的岩土体被各种构造面切割分离成不连续状态时，易导致边坡失稳。

2.4外在诱发因素

在发展农业节水方面，晋城市引入了“利用就是保护”煤矿排水利用新理念，市政府出台了《关于利用煤矿废水发展农业节水灌溉的实施办法》，要求煤矿企业要支持兴建蓄水工程，收集煤矿排水，就近发展农业节水园区，简称“一矿一池一园区”工程。为促进项目的落实，各级水利部门编制了采煤排水利用规划，实行以工补农、以煤补水的优惠政策，采取各类农水、农业资金捆绑运作，分级配套实施。该项目的实施，遏制了地下水无序排放，提高了资金使用效率和水资源利用率。

2.4.1自然因素

地震可以引起岩土体结构和强度的变化。

水使岩土软化或溶蚀，降水一方面恶化边坡围岩的力学性能，另一方面降低围岩的有效应力，从而更易屈服失稳。

2.4.2人为活动

施工中的爆破行为、刷破、开挖等，都会引起岩土力学性质的相应改变，诱发边坡失稳。

3边坡失稳突发事件统计及范例推理评估

影响边坡稳定性的因素众多，但对某一区域或某一类型的边坡稳定性，并非上述所有影响因素都对其起重要作用，为便于范例推理的应用，需对影响因素作一定取舍和细化。根据英国专家Stead1984年对露天矿失稳边坡统计结果，影响岩石边坡稳定性的主要因素一般不超过5个[5]。

3.1边坡失稳突发事件统计

采用文献[6]中14个圆弧形滑坡的实例进行，对目标范例进行范例推理，以岩土容重、边坡高度、内摩擦角、内聚力、边坡角、孔隙水压力、边坡稳定系数作为边坡稳定性的主要影响因素。边坡稳定性范例统计如表1。

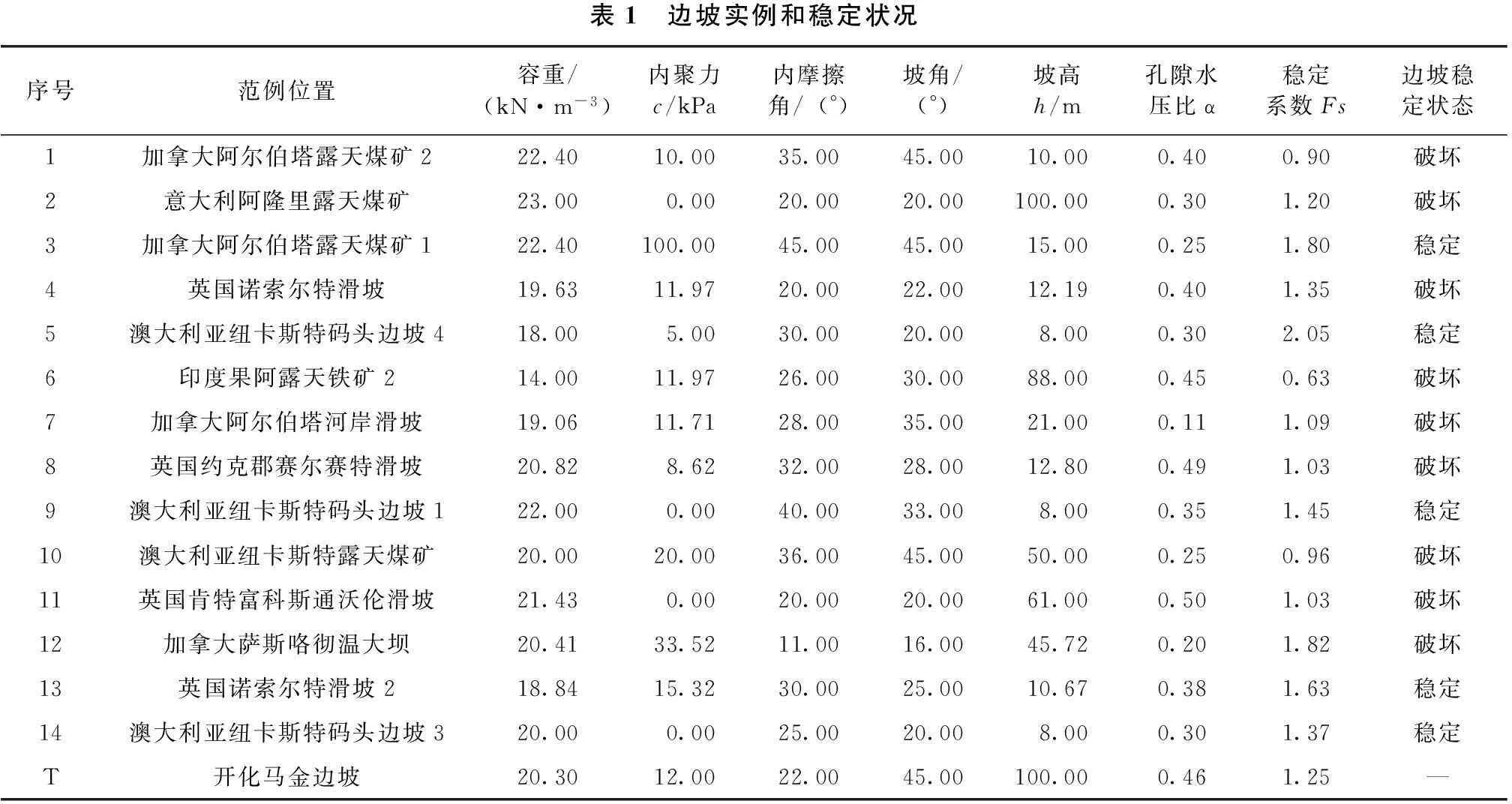
表1 边坡实例和稳定状况序号范例位置容重/(kN·m-3)内聚力c/kPa内摩擦角/(°)坡角/(°)坡高h/m孔隙水压比α稳定系数Fs边坡稳定状态1加拿大阿尔伯塔露天煤矿222.4010.0035.0045.0010.000.400.90破坏2意大利阿隆里露天煤矿23.000.0020.0020.00100.000.301.20破坏3加拿大阿尔伯塔露天煤矿122.40100.0045.0045.0015.000.251.80稳定4英国诺索尔特滑坡19.6311.9720.0022.0012.190.401.35破坏5澳大利亚纽卡斯特码头边坡418.005.0030.0020.008.000.302.05稳定6印度果阿露天铁矿214.0011.9726.0030.0088.000.450.63破坏7加拿大阿尔伯塔河岸滑坡19.0611.7128.0035.0021.000.111.09破坏8英国约克郡赛尔赛特滑坡20.828.6232.0028.0012.800.491.03破坏9澳大利亚纽卡斯特码头边坡122.000.0040.0033.008.000.351.45稳定10澳大利亚纽卡斯特露天煤矿20.0020.0036.0045.0050.000.250.96破坏11英国肯特富科斯通沃伦滑坡21.430.0020.0020.0061.000.501.03破坏12加拿大萨斯咯彻温大坝20.4133.5211.0016.0045.720.201.82破坏13英国诺索尔特滑坡218.8415.3230.0025.0010.670.381.63稳定14澳大利亚纽卡斯特码头边坡320.000.0025.0020.008.000.301.37稳定T开化马金边坡20.3012.0022.0045.00100.000.461.25—

3.2基于范例推理的边坡失稳突发事件风险评估

某国道K1694+830～K1694+960段边坡，位于浙江省开化县马金镇西北方向约15km处，岭里-毛凹一带，边坡高100m，区域内工程地质和水文地质条件复杂多变，土层比较杂乱，碎石含量不均。地层主要为第四系残坡积含碎石粘性土、含粘性土碎石，最大厚度23.6m，下部地层为花岗岩，边坡的坡角为45°，根据地质部门提供的边坡潜在滑动面岩土体的物理力学参数，容重20.3kN/m3，内聚力12kPa，内摩擦角为22°，孔隙水压比为0.46，稳定性系数为1.25。2008年公路改扩建，路堑边坡受到扰动，产生了蠕动变形，需要判断该段边坡是否稳定。

将范例库中前14组数据作为源范例，开化马金边坡数据作为目标范例，根据公式(2)、(3)、(4)对边坡稳定性范例统计表进行归一化处理得表2，对于边坡的稳定状态(评价结果的属性值)进行量化处理，当边坡破坏时为0，稳定时为1。

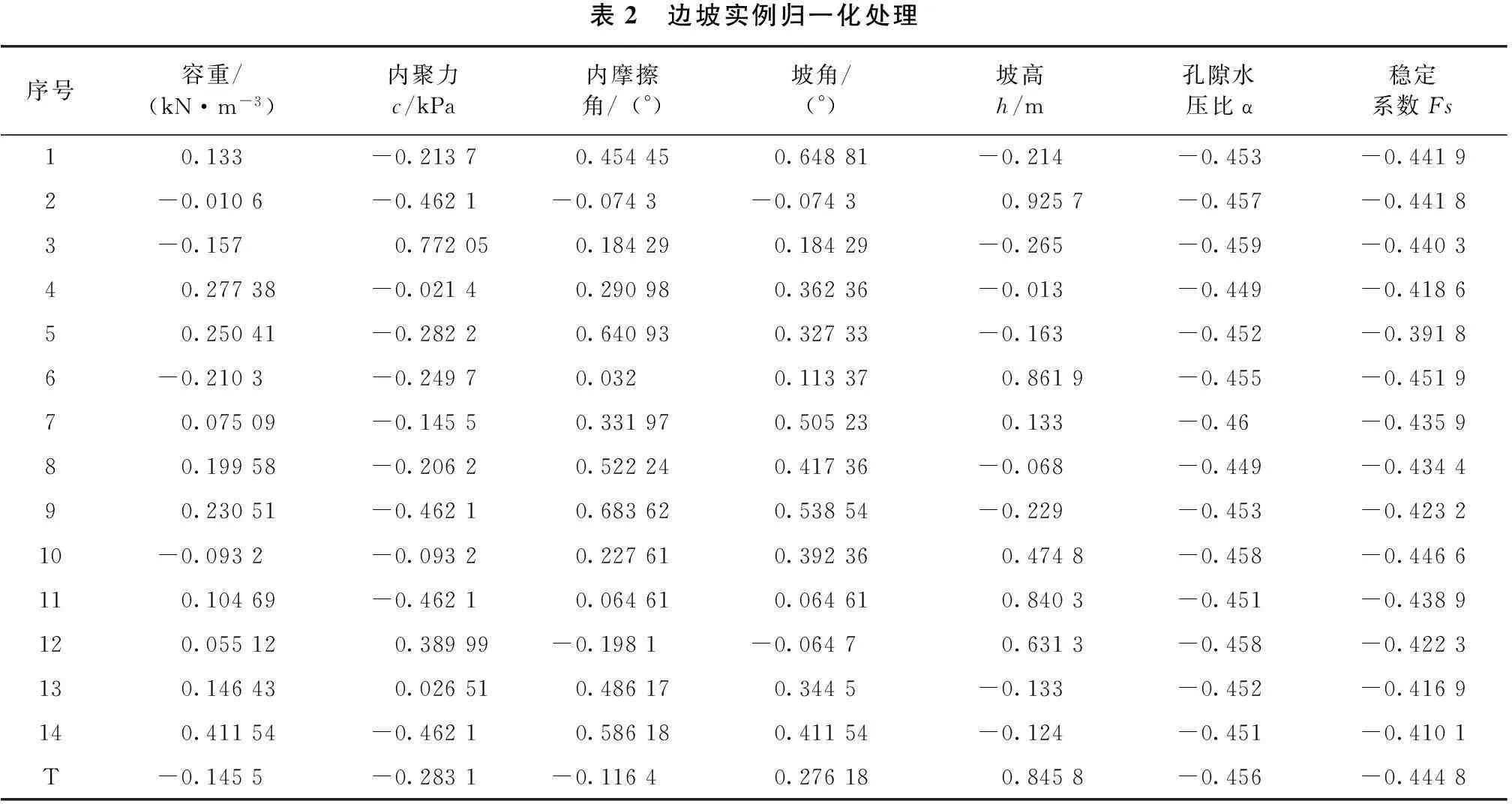
表2 边坡实例归一化处理序号容重/(kN·m-3)内聚力c/kPa内摩擦角/(°)坡角/(°)坡高h/m孔隙水压比α稳定系数Fs10.133-0.21370.454450.64881-0.214-0.453-0.44192-0.0106-0.4621-0.0743-0.07430.9257-0.457-0.44183-0.1570.772050.184290.18429-0.265-0.459-0.440340.27738-0.02140.290980.36236-0.013-0.449-0.418650.25041-0.28220.640930.32733-0.163-0.452-0.39186-0.2103-0.24970.0320.113370.8619-0.455-0.451970.07509-0.14550.331970.505230.133-0.46-0.435980.19958-0.20620.522240.41736-0.068-0.449-0.434490.23051-0.46210.683620.53854-0.229-0.453-0.423210-0.0932-0.09320.227610.392360.4748-0.458-0.4466110.10469-0.46210.064610.064610.8403-0.451-0.4389120.055120.38999-0.1981-0.06470.6313-0.458-0.4223130.146430.026510.486170.3445-0.133-0.452-0.4169140.41154-0.46210.586180.41154-0.124-0.451-0.4101T-0.1455-0.2831-0.11640.276180.8458-0.456-0.4448

根据权值公式计算各属性的权重值wi，得w1=0.055 5；w2=0.104 3；w3=0.149 0；w4=0.144 2；w5=0.167 4；w6=0.194 8；w7=0.184 8。

最后利用相似度公式(1)计算diT，得表3。从表3可以看出该边坡与范例库中第6个源范例的相似度绝对值最小，且为负值，所以开化马金边坡比最相似的源范例边坡稳定性差。因为第6个源范边坡破坏，开化马金边坡有可能出现较大坍方，建议采取必要的措施进行加固和防护，避免滑坡。

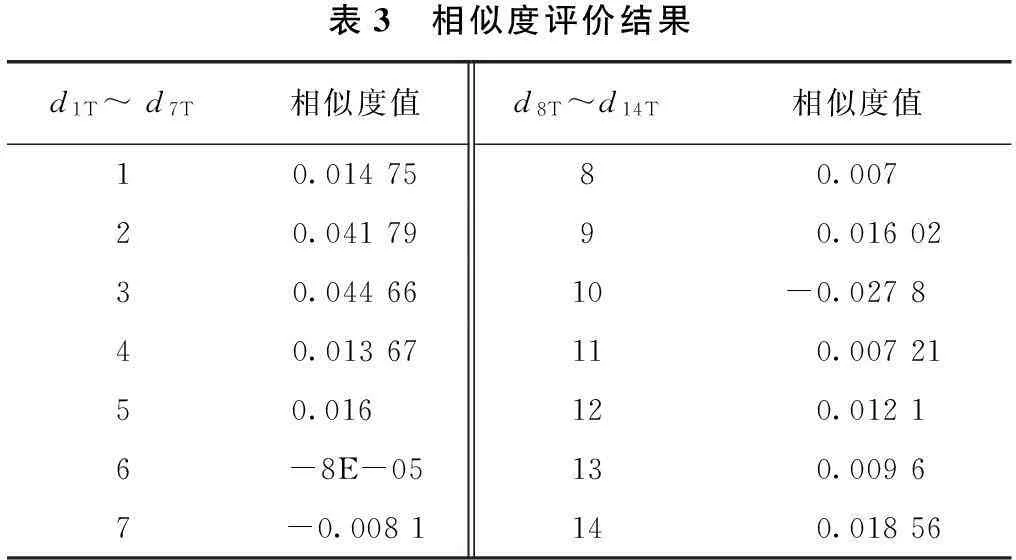
表3 相似度评价结果d1T～d7T相似度值d8T～d14T相似度值10.0147580.00720.0417990.0160230.0446610-0.027840.01367110.0072150.016 120.01216-8E-05130.00967-0.0081140.01856

4结论

1) 范例推理不需要明确的模型，可以应用于没有明确模型的领域，使用方便简单。

2) 边坡过陡、地下水入渗导致空隙水压力增大以及岩土体强度劣化使开化马金边坡存在失稳的风险。建议采用有效支挡结构、削坡减载及封闭坡面对边坡进行处治。

参考文献：

[1] 夏元友，李梅.边坡稳定性评价方法及发展趋势[J].岩石力学与工程学报，2002，21(7)：1087-1091.

[2] 戴文站.基于三层BP网络的多指标综合评估方法及应用[J].系统工程理论与实践，1999，19(5)：29-40.

[3] 夏元友，李梅，谢全敏.基于实例类比推理的边坡稳定性评价方法[J].岩土力学，2003，24：300-303.

[4] 倪志伟，贾瑞玉，李龙澎.基于神经网络的范例推理[J].微机发展，2001(5)：3-7.

[5] 刘瑞华，黄光庆.国道321线七宝莲边坡失稳机制与整治措施[J]，热带地理，2001，21(1)：41-44.

[6] SahN K，Sheorey P R，Upadhyaya LN.Maximum likelihood estimation of slope stability[J].International Journal of Rock MechanicsMining Science & GeomechanicsAbstract，1994，31(1)：47-53.

中图分类号：U 416.1+4

文献标识码：A

文章编号：1008-844X(2016)01-0028-04