空间点群目标相似度计算模型及应用
梁哲恒,谢辉荣,谢刚生
(1. 广东南方数码科技股份有限公司,广东 广州 510665; 2. 华南农业大学,广东 广州 510640)
空间点群目标相似度计算模型及应用
梁哲恒1,谢辉荣2,谢刚生1
(1. 广东南方数码科技股份有限公司,广东 广州 510665; 2. 华南农业大学,广东 广州 510640)
Study on the Calculation Model of Spatial Grouped Point Object Similarity and Its Application
LIANG Zheheng,XIE Huirong,XIE Gangsheng
摘要:为了研究点群目标的相似性问题,整合了与点群目标有关的拓扑关系、方向关系、距离关系、分布范围和分布密度5种要素,这5种要素是影响点群目标相似度的主要因子。根据这5种因子的特点,提出了各个因子相似度的计算模型,最后得到了点群目标之间相似度的总体计算模型。经过验证,该方法能准确地计算点群目标之间的相似程度,符合人们的日常认知。
关键词:空间关系;相似性;点群目标
空间目标的相似性在人类认知过程中具有重要的作用,是进行归纳、分类和类比的基础。空间目标的相似性在空间认知中起着同样的作用[1]。同一尺度空间下的不同目标之间,相似性的研究可以提供空间数据的查询和检索[2]、数据集成和互操作[3]、数据挖掘等方面的应用;并在不同尺度空间下的同一目标进行匹配和综合质量评价[4]。
在心理学和认知科学中,相似关系研究得较多,但在地理空间中的应用,相似关系一直以来研究得较少。一方面由于空间相似关系比较复杂、可计算性差[5],地理空间的相似关系的计算要考虑的因素很多,如空间关系、空间分布、几何特征、语义特征等[1]。空间相似关系研究与模式识别、图像检索密切相关。模式识别中主要针对单一目标的相似性研究[6],图像检索主要是以栅格图像为主[7]。国内外学者作了诸多探讨和研究,如Bruns等引入心理学中的变换模型[8];Li等在此基础上引入拓扑关系、方向关系和距离关系,并提出计算模型[1]。
点群目标是空间目标的重要组成部分,有一定的研究价值[9]。本文考虑到视觉识别的Gestalt原则,以及影响空间点群目标的拓扑关系、距离关系、方向关系、分布范围和分布密度,对空间点群目标相似度进行整体度量,并以试验验证结果的可靠性。
一、点群信息与点群相似度
1. 相似度的定义
Holt在考虑了空间尺度和空间上下文关系之后,对空间目标相似度的定义如下:在某一特定的粒度(比例尺)和内容(专题属性)上被认为是相似的两个区域。但该定义过于笼统和模糊,文献[4]用集合学的方法对空间相似性进行了定义,具有清晰的数学描述。
2. 点群信息
空间目标可以从目标属性、空间变量和几何特征[9]等几个角度认识。点群目标的信息普遍由统计信息、专题信息、拓扑信息、度量信息[10]决定,但根据Bruns提出的观点,空间目标的几何特征中拓扑关系、方向关系和距离关系是最关键的几个因素[11],应该突出某些参数的重要性。因此,本文分别从空间拓扑关系、空间方向关系、空间距离关系、点群分布范围、点群分布密度[8]几个方面进行研究,最后得到计算点群相似度的公式。
二、点群目标相似度的计算方法
点群目标具有聚合的性质,其分布轮廓与凸壳有密切联系,因此用凸壳来逼近点群的全局结构[11]。凸壳是覆盖点群目标的最小凸图形,在实际的应用中,凸壳起着重要作用,如公路规划中,各个乡、镇、村建立点集凸壳,可科学规划环形公路;且凸壳直径具有一定的方向性,符合人们的日常认知。本文对点群目标建立凸壳,计算凸壳的直径,并通过凸壳直径确定定长值K;以凸壳直径与水平方向的夹角来表示方向;在此基础上,用凸壳的面积与点群的点的个数计算点群的分布范围和分布密度。如图1、图2所示。
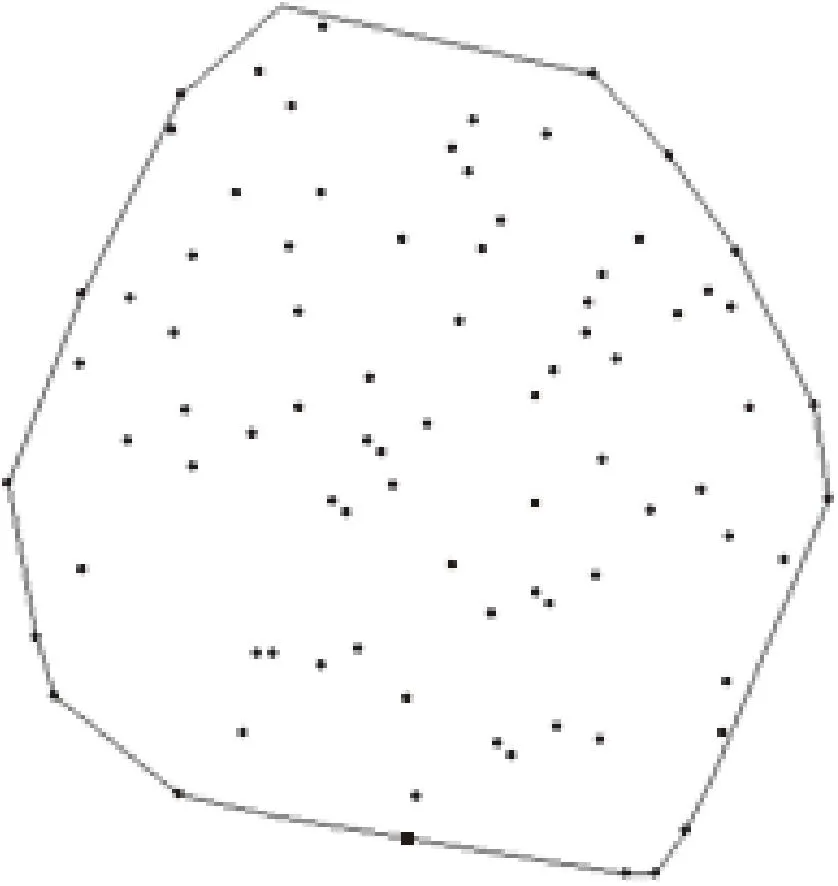
图1 点群目标的凸壳

图2 凸壳直径
1. 拓扑相似度
点群之间的拓扑关系可以用点的邻居来表示,如图3所示。点的邻居可以是定长距离邻居、k个最近邻居、Voronoi邻居等。选择定长距离邻居作为点群拓扑信息的描述参数,主要是由于可以根据实际情况设定邻居的长度。通过尝试不同的定长距离d,记录每个点的拓扑邻居个数,拓扑相似度的计算公式为
(1)
式中,D为点群目标邻居的数量;n为点群目标点的个数。
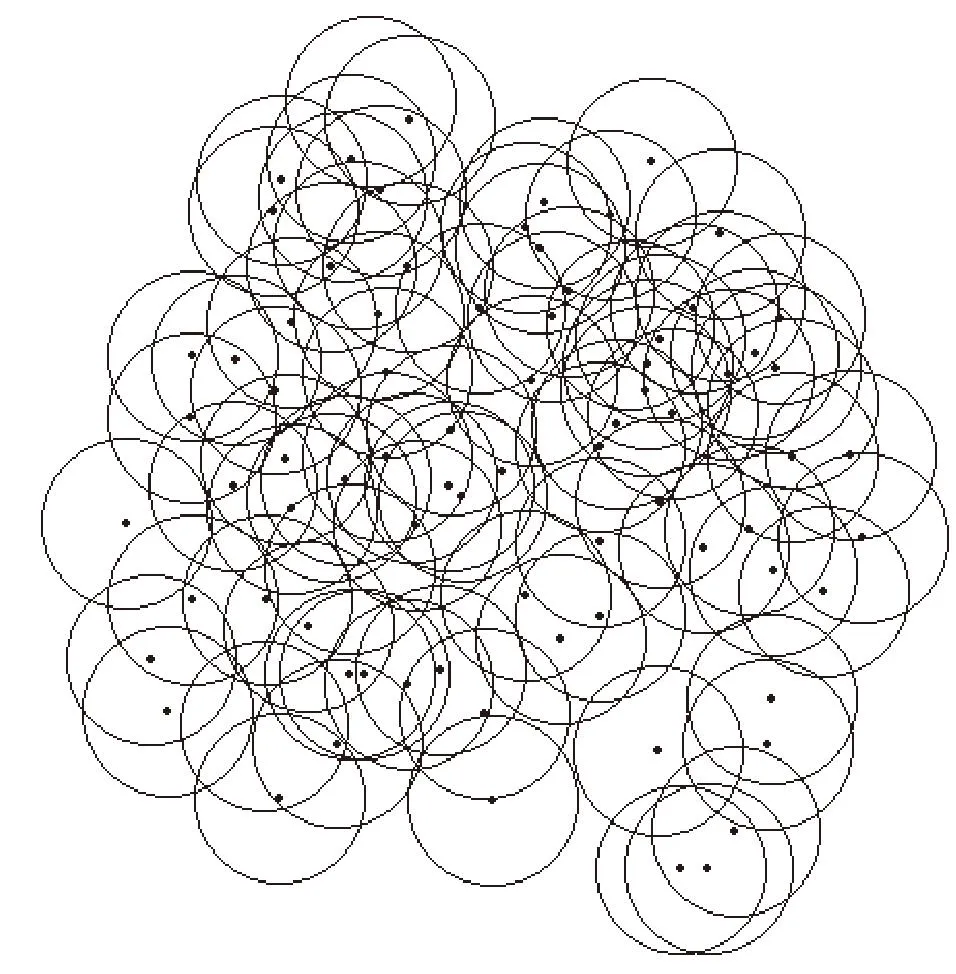
图3 点群的拓扑邻居
2. 方向关系相似度
点群的方向可以表示点群目标分布的大体趋势,点群凸多边形的直径可以看成点群分布的主要方向,用凸壳多边形的直径与水平线之间的夹角θ表示点群目标分布的方向,θ取值范围为[0,π]。当两凸壳直径夹角相差180°时,两目标的相似度为1,这符合人们的认知。其相似性的公式为
(2)
式中,θ1、θ2分别为点群目标凸壳直径与水平线的夹角。
3. 分布范围相似度
在点群周围构建凸壳,凸壳的面积大致能够反映点群的分布范围。点群目标的分布范围大致上可以用凸壳的面积S计算,其公式如下
(3)
式中,S为点群的凸壳面积。
4. 点群分布密度相似度
点群目标的分布密度可以表示点群分布的疏密程度。点群密度的计算公式为点群数目与凸壳面积的比值。其点数与凸壳面积的比值大致上表示点群的分布密度,因此,可以用以下公式表示点群的分布密度相似度
(4)
5. 距离关系相似度
计算点群目标的距离相似度,本文借助的是最小外接矩形(minimum bounding rectangle, MBR)。点群目标的最小外接矩形能够大致反映点群目标分布的形状及集中程度,如图4所示。做出点群目标的最小外接矩形,求出外接矩形的长和宽,由此可求得
(5)
式中,A、B为MBR的长和宽。其中MBR长和宽的比值反映了点群目标的分布的密集程度。

图4 最小外接矩形
6. 点群目标相似度的计算
考虑到点群目标的几何特征,对点群目标进行总体计算,其计算公式如下
(6)
上式为点群目标相似性的整体计算模型。根据数值分析和概率论的研究,几何平均值要比算术平均值在处理差异性方面更加具有稳定性,因此,对点群目标的总体相似性应用几何平均值。
三、试验和结论
为了验证点群相似程度算法的正确性,选择某公交站点的分布情况。图5为几年前的公交车站的分布情况,图6为现在公交车站的分布情况,图7为不相关的某些点集。分别对这3个点群求各个因子的相似度及总体相似度,结果见表1、表2。

图5 点群1

图6 点群2

图7 点群3
由表1可知,点群1和点群2之间的各因子的度量结果都比较接近,点群1与点群3之间、点群2与点群3之间的各个度量值差距比较大。

表1 各因子的统计结果

表2 点群各影响因素的相似度及总体相似度
由表2的计算结果可以得到以下结论:
1) 点群1和点群2之间各个因素的相似度都很高,说明同一点群目标在一定的时间段内的变化不大。
2) 点群1与点群3之间,点群2与点群3之间的各要素相似程度都很小,说明互不相关的点群目标之间相关程度很小。
3) 点群1和点群2之间的分布密度相似度很小,由于在同一区域,点群数目的变化比较大,而点群目标的影响范围变化不大,导致计算点群目标之间的分布密度相似度时,出现不一致性。
4) 此结果符合人们的日常认知,可以作为比较两个点群目标之间相似度的一般方法。
四、结束语
本文提出点群目标之间相似度的计算模型,并通过试验证明了此算法可以较为准确地计算点群目标之间的相似程度,为同一尺度下的不同目标之间的数据查询、互操作、数据挖掘方面提供支持,希望对实际的计算分析能提供一定的参考。
参考文献:
[1]LI B,FONSECA F. TDD-A Comprehensive Model for Qualitative Spatial Similarity Assessment[J]. Spatial Cognition & Computation an Interdisciplinary Journal,2006,6(1):31-62.
[2]GOODCHILD M F, EGENHOFER M J, KEMP K K, et al. Introduction to the Varenius project.[J]. International Journal of Geographical Information Science, 1999, 13(8):731-745.
[3]FRONTIERA P, LARSON R, RADKE J. A Comparison of Geometric Approaches to Assessing Spatial Similarity for GIR[J]. International Journal of Geographical Information Science, 2008, 22(3):337-360.
[4]闫浩文,褚衍东.多尺度地图空间相似关系基本问题研究[J].地理与地理信息科学,2009,25(4):42-44.
[5]陈春希,凌子燕,廖超明.基于遥感与GIS技术的景观格局自相似性的尺度效应研究——以防城港市为例[J].测绘通报,2012(5):50-52.
[6]陈飞,张荣,何华贵.城市多尺度空间数据库的实现方法[J].测绘通报,2014(S2):252-255.
[7]郭仁忠.空间分析[M].北京:高等教育出版社,2001:240-244.
[8]ARKIN E M, CHEW L P, HUTTENLOCHER D P, et al.An Efficiently Computer Metric for Comparing Polygonal Shapes [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1991, 3(13):209-215.
[9]WANG J Z, LI J, WIEDERHOLD G. Simplicity: Semantics-Sensitive Integrated Matching for Picture Libraries[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2001, 9(23):947-963.
[10]BRUNS H T, EGENHOFER M J. Similarity of Spatial Scenes[C]∥Seventh Symposium on Spatial Data Handling.London:[s.n.], 1998:31-42.
[11]刘涛,杜清运,闫浩文.空间点群目标相似度计算[J].武汉大学学报(信息科学版),2011,36(10):1149-1153.
[12]LI Z L, HUANG P Z. Quantitative Measures for Spatial Information of Maps[J]. International Journal of Geographical Information Science, 2002, 16(7):699-709.
[13]毋河海.凸壳原理在点群目标综合中的应用[J] .测绘工程,1997,6(1):1-6.
[14]郝燕玲,唐文静,赵玉新,等.基于空间相似性的面实体匹配算法研究[J].测绘学报,2008,37(4):501-506.
中图分类号:P208
文献标识码:B
文章编号:0494-0911(2016)03-0111-04
作者简介:梁哲恒(1977—),男,硕士,工程师,主要研究方向为GIS软件开发管理。E-mail:zheheng.liang@southgis.com
收稿日期:2015-11-16; 修回日期: 2016-01-07
引文格式: 梁哲恒,谢辉荣,谢刚生. 空间点群目标相似度计算模型及应用[J].测绘通报,2016(3):111-114.DOI:10.13474/j.cnki.11-2246.2016.0100.

