一种基于单接收机旋转的北斗快速精确定向新方法
张成军,许其凤,王永明,杜国成,王慧静
(1. 第二炮兵装备研究院,北京 100095; 2. 信息工程大学,河南 郑州 450001)
一种基于单接收机旋转的北斗快速精确定向新方法
张成军1,许其凤2,王永明1,杜国成1,王慧静1
(1. 第二炮兵装备研究院,北京 100095; 2. 信息工程大学,河南 郑州 450001)
A New Approach of BDS Fast and Accurate Orientation Based on a Single Rotaing Receiver
ZHANG Chengjun,XU Qifeng,WANG Yongming,DU Guocheng,WANG Huijing
摘要:利用1台北斗接收机以一定的臂长和角速率围绕固定中心旋转,解决了定向中北斗卫星导航系统中5颗GEO卫星静止不动和观测时间短造成的观测方程复共线性问题,推导了定向的基本原理,并概要设计了定向系统。仿真结果表明,在3 min时间内定向精度可优于10 s;在利用GPS接收机进行物理仿真时,实现的外符合定向精度优于80 s。
关键词:北斗卫星导航系统;大地方位角;定向精度;物理仿真
传统的卫星定向技术一般是利用两台GNSS接收机架设于空间两点形成短基线,由基线矢量直接得到其大地方位角[1-6]。在军事上由于地形大小、载车长度等因素影响[7-8],基线长度受限,这直接影响了GNSS定向的精度;对于北斗卫星导航系统而言,在地固系下GEO卫星几乎是静止不动的,IGSO卫星的角速度也较传统的MEO卫星小,当接收机静止时,接收的载波相位观测值变化微弱,需较长的初始化时间才能准确分离整周模糊度参数[9-12],影响定向的速度。本文利用1台北斗接收机以固定臂长和角速率围绕旋转中心旋转,以解决上述难题,利用角度测量的精度约束提升虚拟基线的定向精度,通过主动运动促使接收机观测值变化,减弱观测方程病态,提升解算速度[13];该方法可精确解算出角度传感器(如经纬仪)度盘零点的大地方位角,使用时只需照准目标,读取水平度盘的方向观测值,然后将二者相加即可给出照准方向的大地方位角。
一、定向原理
设有1台北斗接收机,它绕P点以臂长R为半径作匀速运动。此时,测站坐标系设为北东天坐标系,即X轴指向正北方向,Z轴指向天顶,Y轴垂直于XOZ平面并与X轴和Z轴成左手坐标系(如图1所示)。
卫星S到接收机瞬时位置Pi的观测方程可写为
(1)
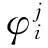

图1 接收机旋转状态下载波相位观测值

(2)
在北东天坐标系中,Δρj又可写为

(3)
将式(3)和式(2)代入式(1)中,可得

(4)
式中,Δx、Δy和Δz为旋转中心至接收机天线相位中心的3个分量。接收机旋转时,其运动状态如图2所示。
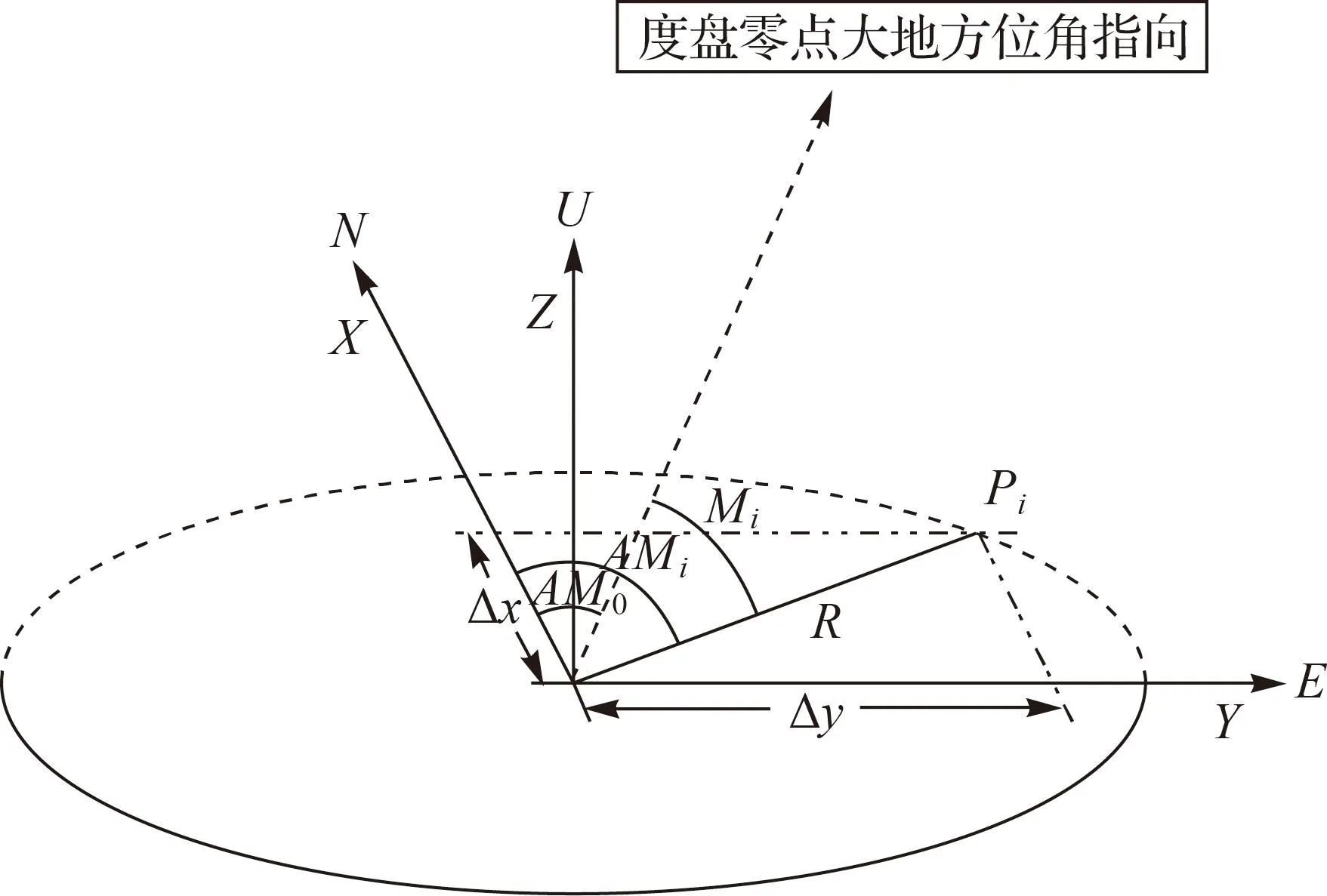
图2 接收机旋转时大地方位角变化
图中,AM0为角度传感器(如经纬仪)度盘零点的大地方位角,Mi(ti)为ti时刻角度传感器的度盘读数,AMi为ti时刻角度传感器对应的大地方位角,R为旋转的半径。
则Δx、Δy、Δz可表示为
(5)
于是有

(6)
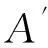
(7)
式中,d为需要解算的度盘零点大地方位角修正值;dr臂长修正值。
当仪器整平时,ΔZ=0,整理可得
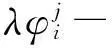
(8)
式(8)即是快速定向的数学模型,式中有3种未知参数,即测站到卫星j的载波相位观测值的整周模糊度Nj,臂长修正值dr和角度传感器零点大地方位角修正值d,共n+2个(n为观测到的卫星个数)。因此,在卫星信号不发生跳变时,只需两个历元数据就可以解算出定向结果。
二、定向系统概要设计
根据上述定向原理,可设计1台快速定向系统,该定向系统可由1台可接收北斗载波相位观测值的GNSS接收机和1台全站仪组成(如图3所示),其中全站仪作为角度传感器实时记录GNSS接收机的旋转角度,北斗接收机接收北斗卫星导航系统载波相位数据。

图3 定向系统设计
三、定向仿真
1. 定向原理可行性评估
为评估基于北斗单接收机旋转的算法的可行性,仿真时选择北斗卫星导航系统中5颗地球同步轨道卫星(GEO)和3颗倾斜轨道地球同步卫星(IGSO),其运行周期为24 h,不同时间其卫星空间分布不同,为使其具有代表性,将全天均匀分为36个测段,每个测段进行36次采样,每次采样观测时间为3 min。仿真点位选在位于东南沿海北纬20°、东经120°位置处,旋臂初值设为1 m。具体仿真条件见表1。仿真结果如图4所示。

图4 定向可行性精度分析
从图4可以看出,利用提出的新方法可以正确解算出结果,且定向的精度较高(标准差STD仅为9.51 s)。

表1 不同地区定向仿真条件
2. 北斗覆盖重点区域内定向精度评估
同一测段不同地区观测的卫星空间分布不同,同样条件其解算精度也会有所不同。为了考察不同地区的定向精度,选择我国北斗卫星导航系统的重点覆盖区域(北纬10°—55°,东经75°—150°),以2°×2°的地理分辨率进行仿真,每个点进行同样条件的36测段×36次仿真,如图5所示。

图5 北斗导航系统重点覆盖区内定向精度分析
可见,在我国北斗卫星导航系统覆盖区域内,仿真的定向标准差都小于40角秒,并且在重点覆盖区域内绝大部分的标准差都优于10角秒;非重点覆盖区域内定向仿真精度不高,这主要是因为在非重点覆盖区内可见卫星数较少,且其空间几何分布状态也较差所致。
3. 观测时间对定向精度影响分析
观测时间长度不同,北斗卫星在空中的几何分布不同,并且用于解算的数据量也不相同,其定向精度也必然有所不同。为有效地克服缩短观测时间与提高定位精度这一对矛盾,需要确定合理的观测时间。在仿真中,其他条件不变,仅将观测时间进行变化,仿真结果如图6所示。
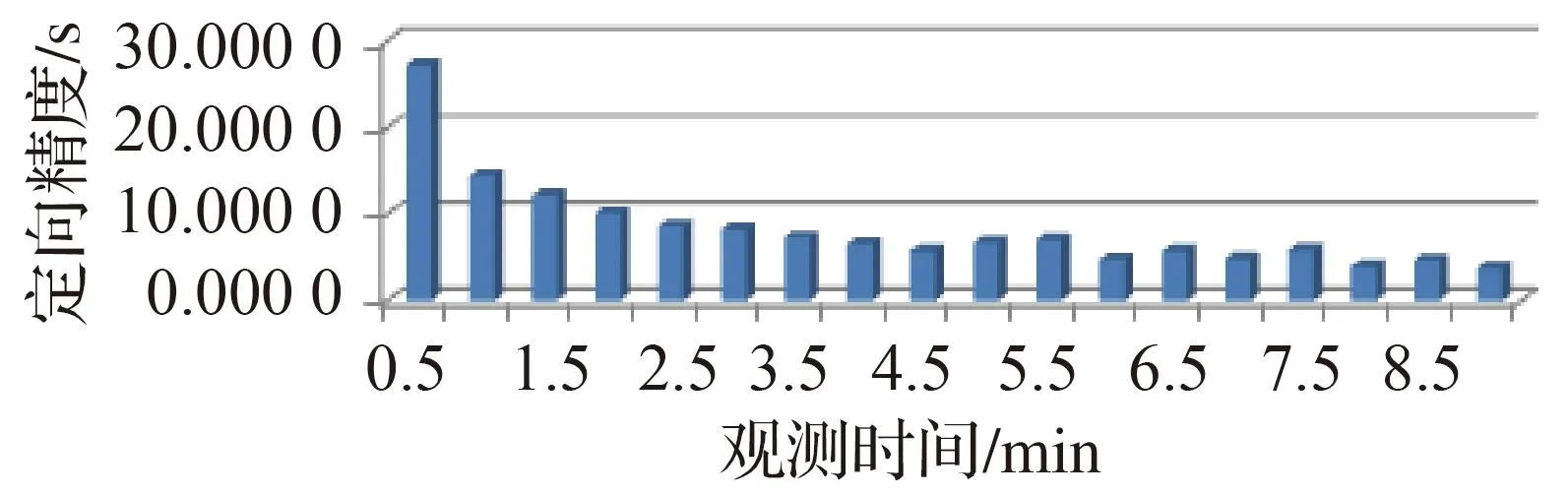
图6 不同观测时间对定向精度影响
由图6可知,当观测时间延长至3 min以后,定向的精度变化不大,因此建议采用的观测时间为3 min,不仅可以保证精度,还可以体现出速度。
4. 旋臂长度对定向精度影响分析
由定向原理可知,旋臂长度与定向的精度成反比,旋臂越长定向精度越高。但旋臂太长对设备的制造工艺要求高,且容易引入其他误差,因此必须确定合理的旋臂长度。仿真中,将表1中的其他条件不变,仅改变旋臂长度,得到的仿真结果如图7所示。

图7 旋臂长度对定向精度影响
从图7中可见,定向精度随着臂长的增长而提高,但在很多应用中10 s的定向精度已经足够使用,因此综合考虑建议臂长选用为1 m左右即可。
5. 物理仿真
为验证算法的正确性和可行性,设计了一台原型样机,由于GPS系统与北斗导航系统具有高度的相似性,样机中的接收机采用GPS接收机代替,如图8所示。

图8 基于GPS接收机的样机
利用上述原型样机进行了大量试验,将定向结果与基准值比较,得到如图9所示的结果。

图9 物理仿真示例
从图9中可知,定向的外符合精度均优于80 s,经统计其标准差为19 s,满足各种运动载体对定向的需求。
四、结束语
利用1台GNSS接收机结合角度传感器进行定向的新方法,可以克服观测时间短及北斗导航系统中GEO卫星静止等带来的复共线性问题。仿真结果表明,该方法正确可行,在3 min的时间内定向精度可达10 s,当观测时间为3 min、臂长为1 m时,可获得较理想的定向结果;利用设计的样机,在GPS环境下观测3 min,定向的外符合精度优于80 s。该方法可运用于载体的快速定位定向,具有重要的意义。
参考文献:
[1]胡国辉,范胜林,袁信.GPS定位定向系统的研究[J].宇航学报,2000,21(4):111-116.
[2]张成军,许其凤.GPS定向中大地方位角解算问题研究[J].测绘通报,2008(12):8-10.
[3]周江华.贝塞尔大地反解问题的高效率算法[J].测绘学报,2002,31(2):108-111.
[4]熊建明. GPS短边方位测量的精度分析[J].测绘通报, 2000(11):18-20.
[5]王银华,胡小平.GPS精密定向研究的实验[J]. 宇航学报,2001,22(1):70-74.
[6]尤红建,苏林.基于双GPS接收机的精密定向研究[J].中国空间科学技术,2003(3):47-51.
[7]严恭敏.车载自主定位定向系统研究[D].西安:西北工业大学,2006.
[8]白云超,张晓明,吕妍红.一种发射车快速精确定位定向技术的研究[J].测绘科学,2009(2):81-84.
[9]康国华,刘建业,赵伟.基于基线延长的高精度北斗双星系统快速定向算法研究[J].宇航学报,2006,27(6):1191-1195.
[10]逯亮清,胡小平,吴美平.利用旋转基线方法进行双星快速定向[J].宇航学报,2004,25(2):158-162.
[11]唐卫明,李笛,迟凤明.北斗卫星导航系统单历元定向算法研究[J].武汉大学学报(信息科学版),2013,38(9):1014-1017.
[12]李征航,刘万科,楼益栋,等.基于双频GPS数据的单历元定向算法研究[J].武汉大学学报(信息科学版),2007,32(9):753-756.
[13]张成军.基于BD2的快速精确定位定向关键技术研究[D].郑州:信息工程大学,2011.
中图分类号:P228
文献标识码:B
文章编号:0494-0911(2016)03-0018-04
作者简介:张成军(1976—),男,博士后,主要从事卫星导航系统的应用研究。E-mail:zcj218@126.com
基金项目:中国博士后科学基金(2013M542460)
收稿日期:2015-03-05; 修回日期: 2015-11-02
引文格式: 张成军,许其凤,王永明,等. 一种基于单接收机旋转的北斗快速精确定向新方法[J].测绘通报,2016(3):18-21.DOI:10.13474/j.cnki.11-2246.2016.0076.

