采用序列二次规划求解的稳健波束形成新算法

虞泓波,冯大政,解 虎

(西安电子科技大学雷达信号处理国家重点实验室,陕西西安 710071)



采用序列二次规划求解的稳健波束形成新算法

虞泓波,冯大政,解 虎

(西安电子科技大学雷达信号处理国家重点实验室,陕西西安 710071)

摘要:利用尽可能少的先验信息进行导向矢量估计的稳健波束形成方法利用半正定松弛算法求解,面临可能存在性能损失、计算复杂度高的问题,针对该问题提出一种采用序列二次规划求解的新算法.首先利用一阶泰勒级数将原始模型线性近似为凸优化问题,然后对该子凸优化问题进行迭代求解.此外,还考虑了协方差矩阵失配问题,提出最坏情况性能最优的序列二次规划算法提高序列二次规划算法的性能.理论分析和仿真实验表明,序列二次规划算法收敛速度较快,收敛点逼近原始问题最优解,与现有半正定松弛算法相比,能够有效降低计算量,该算法在小参数值时即可有效改进序列二次规划算法的性能.

关键词:导向矢量估计;稳健波束形成;序列二次规划;线性近似;最坏情况性能最优

自适应波束形成是阵列信号处理中的一项重要任务,为了提高波束形成器的性能,近年来稳健的波束形成方法得到深入研究.文献[1]提出了基于最坏情况性能最优(Worst-Case)的稳健自适应波束形成方法;文献[2]针对非相干散射信号源稳健波束形成问题,提出了一种均匀线阵下通用信号模型稳健波束形成算法;文献[3]基于导向矢量失配模型,提出一种迭代求解算法,以估计期望信号导向矢量;文献[4-5]提出了基于协方差矩阵重构的稳健波束形成方法,通过重构干扰和噪声协方差矩阵提高了协方差矩阵的有效性,但这类算法目前计算量很大,需要进一步研究降低计算量的方法;文献[6]对文献[3]中的算法进行改进,提出一种半正定松弛(Semi-Definite Relaxation,SDR)算法进行导向矢量估计,与文献[3]中的算法相比,增大了系统自由度,因而具有更高的输出信干噪比(Signal to Interference and Noise Ratio,SINR);文献[6-7]指出SDR算法的先验信息依赖性低于传统的稳健波束形成算法(如文献[1-2]中的算法).

然而,利用SDR算法求解依然面临一些问题.首先,只有当原始问题的解惟一时,松弛后的问题才总会有秩1的最优解[6],但原始问题最优解的惟一性不一定总是成立,这样采用SDR算法求解有可能会造成性能损失;其次,经过松弛后需要对N阶矩阵变量进行凸优化,计算复杂度很高,不利于工程实际应用.文中提出采用序列二次规划(Sequential Quadratic Programming,SQP)对原始问题进行求解,首先利用一阶泰勒公式将原始问题线性近似为一个子二阶锥规划(Second-Order Cone Programming,SOCP)问题,然后迭代求解子SOCP问题,此外,还考虑了协方差矩阵失配问题,提出最坏情况性能最优的序列二次规划(SQP-WC)算法来提高SQP算法的性能.

1 采用SQP求解的稳健波束形成

1.1 SQP算法

假设一个阵列包含N个阵元,空间远场处有P个信号源,则阵列的接收数据矢量可以表示为

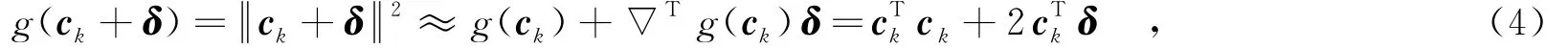
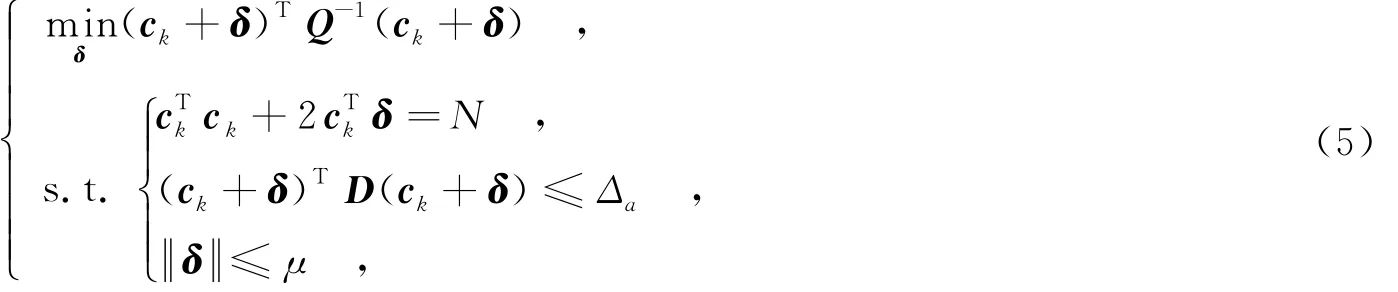
将ck+δ代入代价函数式(3)中,并结合式(4)可以得到代价函数,即增加变量δ的模约束,是为了使得每次更新的δ不至于过大.容易看出,代价函数式(5)为一个SOCP问题,利用内点法容易求解.因此,假设经过k次迭代得到ck后,可以利用代价函数式(5)求解增量δ,然后将ck+1= ck+δ作为新的初值进行求解.综上所述,文中所提SQP算法的计算步骤可以概括为:

(1)给定初值c0及迭代停止参数β,0＜β≪1;

(2)将ck-1代入代价函数式(5),求解凸优化问题式(5),得到最优解δk;

继续执行步骤(2)至(3).

1.2 SQP-WC算法

假设R是真实协方差矩阵,那么采样协方差矩阵与真实协方差矩阵的失配关系可以描述为[8]

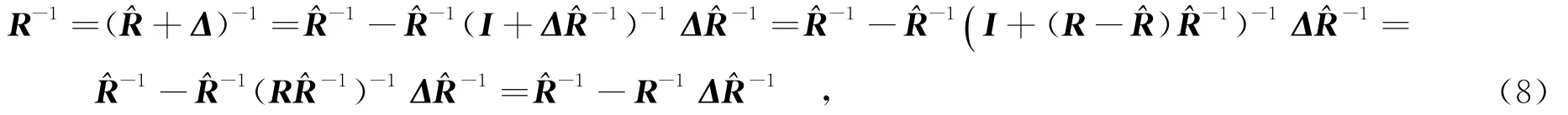
其中,I为N阶单位矩阵.观察式(8)容易发现,由于R与^R均为Hermit矩阵,令Δ1= -R-1Δ^R-1,则逆矩阵失配量Δ1必为Hermit矩阵,根据Cauchy-Schwartz不等式,有

这里利用了R为固定值这一信息.类似于文献[8],最坏情况性能最优的导向矢量估计方法可以写为

利用文献[8]中的结果,最坏情况性能最优序列二次规划算法(SQP-WC)经过k次迭代后的线性近似为

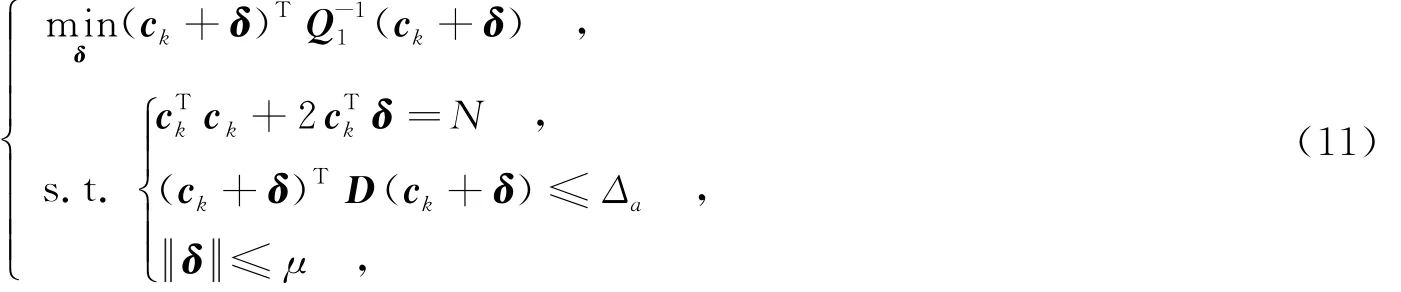
2 初始值的选取

从第1节模型推导过程中可以看出,初始值离最优解越近,在一定的增量模上限下其收敛速度会越快.虽然假定导向矢量与真实导向矢量之间存在失配,但通常考虑的失配量相对较小,因此假定导向矢量已经比较接近真实的导向矢量,由此,代价函数式(5)与式(11)的一个较好的初值可以由假定导向矢量¯a得到,即

所以文中SQP与SQP-WC算法中,可以将假定的导向矢量分别作为两种算法的初值.

3 收敛性说明及计算复杂度分析

需要说明的是,由于文中算法是对约束中的非凸约束进行线性逼近,因此,会收敛到一个局部最优解[8],但从第4节的系列仿真实验可以看出,文中方法求得的解非常接近文献[6]中SDR方法的解.从仿真实验可以看出,经过6步左右,文中方法即可收敛,这样,SQP算法的计算复杂度将远小于文献[6]中的SDR算法.由文献[9]可知,SDR算法的计算复杂度为O( N4.5log(1/ε)),其中ε＞0,为求解精度,而文献[10]综合考虑求解精度的影响,认为SDR算法的计算复杂度甚至高达O(N6),如此高的计算复杂度限制了SDR算法在实际工程中的应用.文中算法的计算复杂度主要在于每次迭代需要求解的子SOCP问题,文献[11]指出求解SOCP的计算复杂度为O(N3.5),那么,文中方法的计算复杂度为O(6N3.5),显然有

由式(13)可知,SQP及SQP-WC算法相对于SDR算法能够有效降低计算复杂度、提高计算效率.

4 仿真实验与性能分析

仿真实验考虑10个阵元的均匀线阵,阵元间距均为半个波长.假设空间远场处存在两个点干扰,分别位于30°与50°,干噪比(Interference and Noise Ratio,INR)均为30 dB,按照文献[8]中方法,加载因子根据=进行设置,其中u称为相对调整因子,符号tr{·}表示求矩阵的迹.仿真实验中将主要考虑两种导向矢量失配场景,一种是波达方向失配,一种是局部相干散射引起的导向矢量失配,由于在实际应用中阵元幅相误差难以避免,因此,在两种场景中都考虑了阵元幅相误差,假设各个阵元幅相误差均服从零均值高斯分布,方差均为0.01.实验中采用100个样本来估计协方差矩阵,除图2和图3外,其余仿真图均为100次实验取平均值的结果.文中所提SQP与SQP-WC算法中增量δ的模上限均设为μ=0.3(对于模增量上限的选取参考了文献[8],在此不作过多讨论),迭代停止参数设为β=0.001.

实验1 假设真实目标信号方向为6°,而假定目标信号方向为3°,也就是说导向矢量存在3°失配.文中算法、SDR算法均选取期望信号角域Θ=[θt-5°,θt+5°]=[-2°,8°].如第3节所述,文中算法的初始值选取为3°时的目标信号导向矢量.

图1给出了4种算法输出SINR随输入信噪比(Signal-to-Noise Ratio,SNR)变化曲线,其中加入经典的Worst-Case[1]算法与对角加载算法(加载采样矩阵求逆(Loading Sample Matrix Inversion,LSMI))进行性能对比,Worst-Case算法的误差界设为εw=0.3N=3,LSMI算法加载量为噪声功率的10倍.从图1可以看出,提出的SQP算法与SDR算法性能曲线几乎吻合,这说明了SQP算法求解原始问题的有效性.图2给出了SQP算法在信噪比为10 dB时的目标函数值随迭代次数变化曲线,从图中可以看出,经过5～6步迭代SQP算法开始收敛,这说明SQP算法求解原始问题需求解较少个数的SOCP问题,相对于SDR算法有效提高了计算效率.

图1 输出SINR随输入SNR变化曲线(实验1)

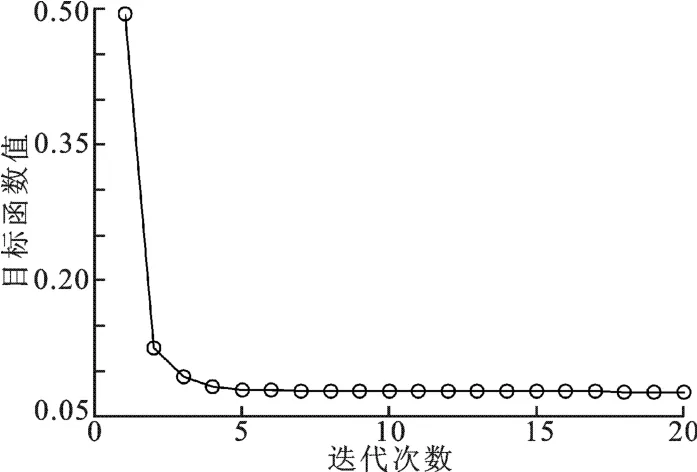
图2 SQP算法收敛曲线,SNR为10 dB(实验1)

图3给出了SQP-WC算法在参数u取不同值时的性能曲线,从图中可以看出,参数u在取得较小值的情况下就可以对SQP算法的性能有一定的改进,在参数u的值较大时SQP-WC算法的性能相当,可以看出,在u=0.5与u=1时,两条曲线几乎吻合.

图4给出了SNR为10 d B时,4种算法输出SINR随样本数变化曲线,样本数变化范围为10到200.从图5可以看出,在整个样本数区间,SQP算法与SDR算法样本收敛曲线几乎重叠,这说明了文中SQP算法收敛点逼近原始问题最优解的特性不随样本数而变化.

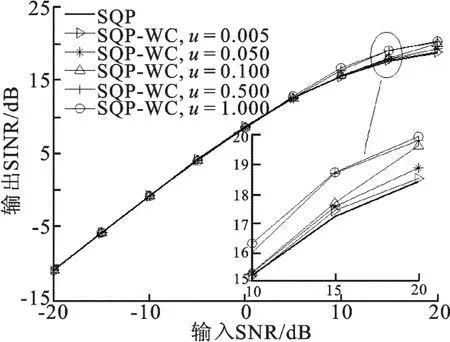
图3 SQP-WC算法在不同参数u下的性能(实验1)

图4 4种算法输出SINR随样本变化曲线(实验1)

实验2 考虑由局部相干散射引起的失配问题,真实的导向矢量由5个信号路径构成,即

其中,a(θ0)表示主路径导向矢量,θ0=3°,a(θi)表示相干散射路径导向矢量,θi,i=1,2,3,4,均在区间[0°,6°]内服从均匀分布,φi,i=1,2,3,4,相互独立且均服从[0,2π]内均匀分布.文中算法与SDR算法的期望信号角域选取如同实验1.图5给出了SQP算法的迭代收敛曲线,从图中可以看出,经过6步迭代算法收敛.图6给出了4种算法输出SINR随输入SNR变化曲线,从图中可以看出,文中SQP算法与SDR算法的曲线几乎重叠,这说明了SQP算法的收敛点逼近原始问题的最优解.图7给出了SQP-WC算法在参数u不同取值情况下的性能,从图中可以看出,u设置为较小值时即可有效改进SQP算法的性能,在u=0.5与u=1时,两条曲线几乎吻合,说明在u取值较大时,SQP-WC算法性能相当.

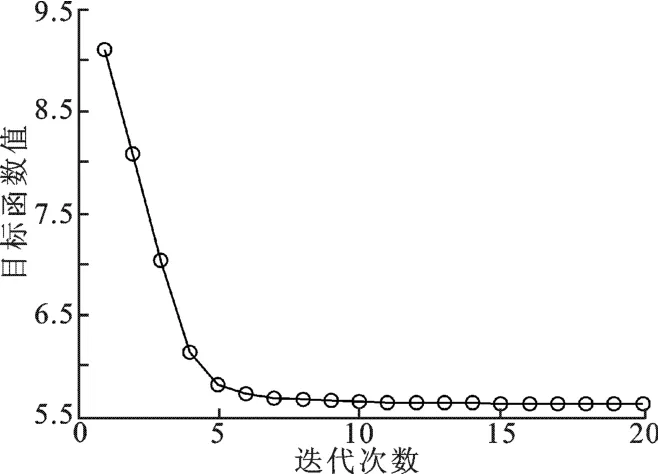
图5 SQP算法收敛曲线,SNR为10 dB(实验2)

图6 输出SINR随输入SNR变化曲线(实验2)

图7 SQP-WC算法在不同参数u下的性能(实验2)

5 结束语

笔者针对传统SDR算法可能存在性能损失及计算复杂度高的问题,提出一种SQP算法来求解原始非凸问题.通过将原始问题中等式非凸约束线性化进而将原始问题转化为一个SOCP问题,然后采用迭代求解子SOCP问题来逼近原始问题最优解,从而降低了SDR算法的计算复杂度,更利于工程应用,仿真实验验证了SQP算法的有效性.此外,文中还考虑了协方差矩阵失配问题,提出另一种SQP-WC算法进一步改进SQP算法的性能.仿真实验说明,在加载参数较小时,即可有效改善SQP算法的性能.

参考文献:

[1]VOROBYOV S A,GERSHMAN A B,LUO Z Q.Robust Adaptive Beamforming Using Worst-Case Performance Optimization:a Solution to the Signal Mismatch Problem[J].IEEE Transactions on Signal Processing,2003,51(2): 313-324.

[2]刘成城,丁永超,赵拥军,等.均匀直线阵下通用信号模型稳健波束形成算法[J].西安电子科技大学学报,2014,41 (5):166-172.LIU Chengcheng,DING Yongchao,ZHAO Yongjun,et al.Robust Beamforming Algorithm for General Signal Models Based on the ULA[J].Journal of Xidian University,2014,41(5):166-172.

[3]HASSANIEN A,VOROBYOV S A,WONG K M.Robust Adaptive Beamforming using Sequential Quadratic Programming: An Iterative Solution to the Mismatch Problem[J].IEEE Signal Processing Letters,2008(15):733-736.

[4]GU Y J,GOODMAN N A,HONG S H,et al.Robust Adaptive Beamforming Based on Interference Covariance Matrix Sparse Reconstruction[J].Signal Processing,2014,96(PART B):375-381.

[5]LI J,WEI G,DING Y H.Adaptive Beamforming Based on Covariance Matrix Reconstruction by Exploiting Interferences’Cyclostationarity[J].Signal Processing,2013,93(9):2543-2547.

[6]KHABBAZIBASMENJ A,VOROBYOV S A,ABOULNASR H.Robust Adaptive Beamforming Based on Steering Vector Estimation With as Little as Possible Prior Information[J].IEEE Transactions on Signal Processing,2012,60 (6):2974-2978.

[7]VOROBYOV S A.Principles of Minimum Variance Robust Adaptive Beamforming Design[J].Signal Processing,2013,93(12):3264-3277.

[8]LIAO B,TSUI K M,CHAN S C.Robust Beamforming with Magnitude Response Constraints Using Iterative Secondorder Cone Programming[J].IEEE Transactions on Antennas and Propagation,2012,59(9):3477-3482.

[9]LUO Z Q,WONG K M,SO A M C,et al.Semidefinite Relaxation of Quadratic Optimization Problems[J].IEEE Signal Processing Magazine,2010,27(3):20-34.

[10]李杰.稳健波束形成与稀疏空间谱估计技术研究[D].广州:华南理工大学,2013.

[11]ZHANG W,WANG J,WU S L.Robust Capon Beamforming against Large DOA Mismatch[J].Signal Processing,2013,93(4):804-810.

(编辑:王 瑞)

Novel robust beamforming algorithm using sequential quadratic programming

YU Hongbo,FENG Dazheng,XIE Hu
(National Key Lab.of Radar Signal Processing,Xidian Univ.,Xi’an 710071,China)

Abstract:Aiming at the probably existing performance loss and high computational complexity of the robust beamforming based on steering vector estimation with as little prior information as possible which is solved by the semi-definite relaxation(SDR)approach,a novel robust beamforming algorithm using sequential quadratic programming (SQP)is proposed.The original non-convex problem is linearly approximated to a convex subproblem using the first order Taylor’s series,and the optimal solution is found out by solving the convex subproblem iteratively.Moreover,considering the mismatch of the sample covariance matrix,the SQP-WC method based on worst-case performance optimization is presented to improve the performance of the proposed SQP method.Theoretical analysis and simulation results show that the proposed SQP algorithm can converge fast and its convergence point approximates the optimal solution to the original problem,which indicates that the SQP method can effectively reduce the computational complexity compared with the SDR method,and furthermore,the SQP-WC method can effectively improve the performance of the SQP method with a small parameter.

Key Words:steering vector estimation;robust beamforming;SQP;linear approximation;worst-case performance optimization

作者简介:虞泓波(1988-),男,西安电子科技大学博士研究生,E-mail:beyond_hongbo@126.com.

基金项目:国家自然科学基金资助项目(61271293)

收稿日期:2014-09-25 网络出版时间:2015-05-21

doi:10.3969/j.issn.1001-2400.2016.02.008

中图分类号:TN958.92

文献标识码:A

文章编号:1001-2400(2016)02-0041-05

网络出版地址:http://www.cnki.net/kcms/detail/61.1076.TN.20150521.0902.005.html