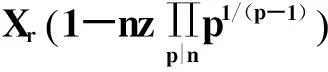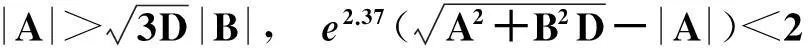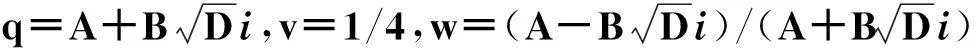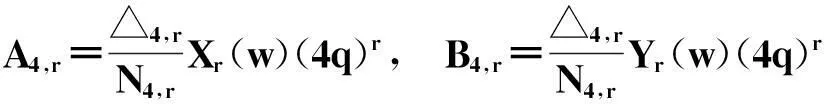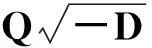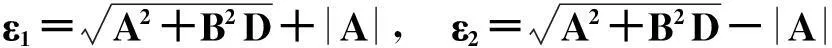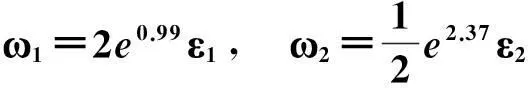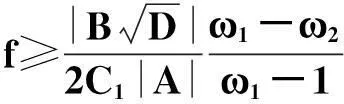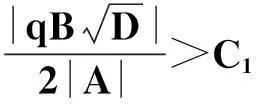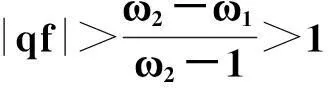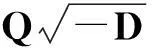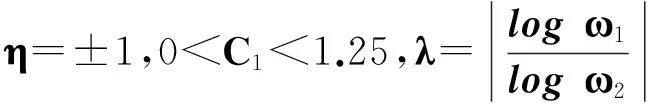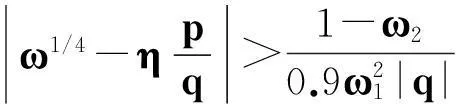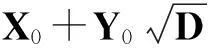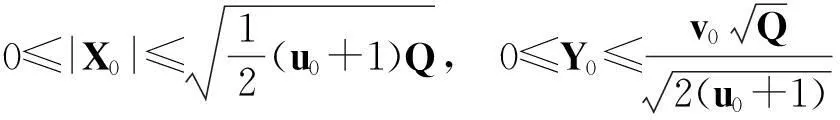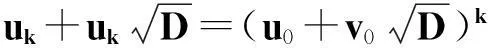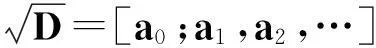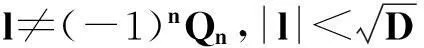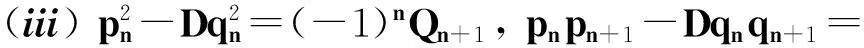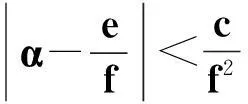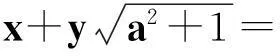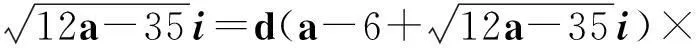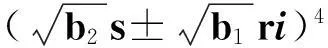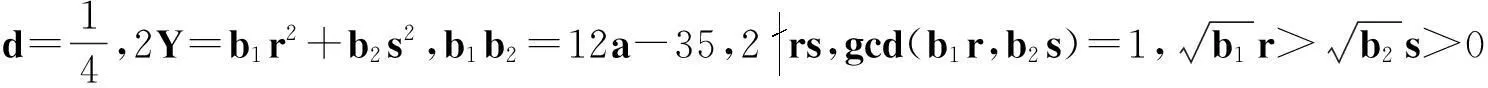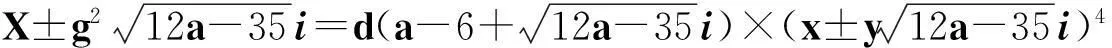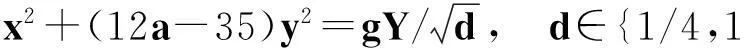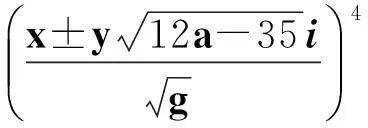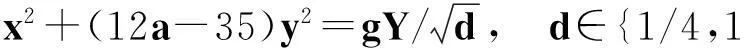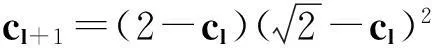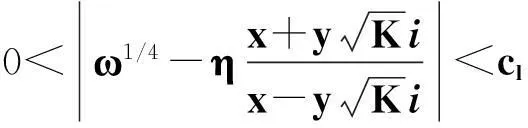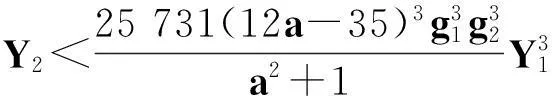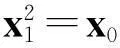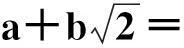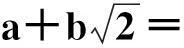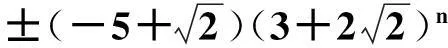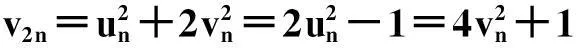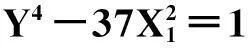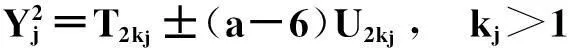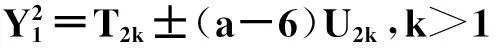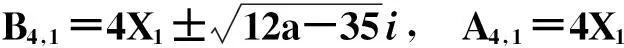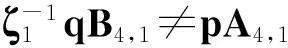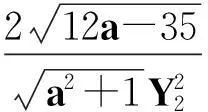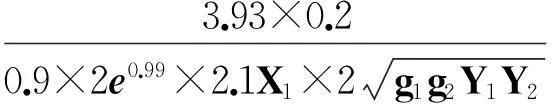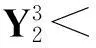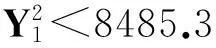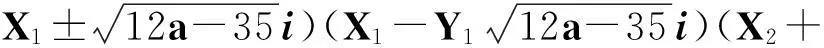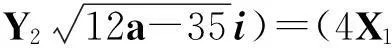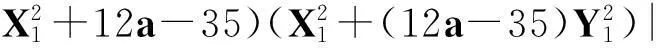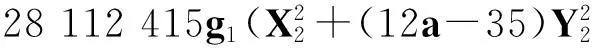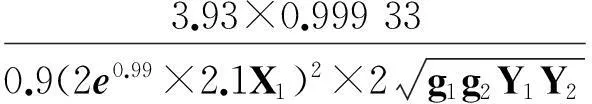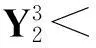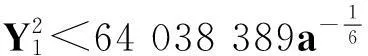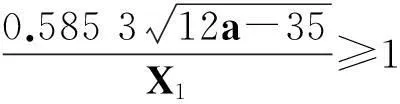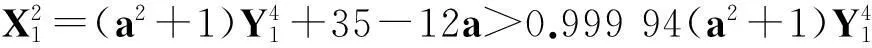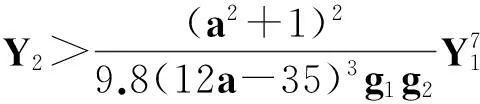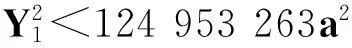关于丢番图方程X2-(a2+1)Y4=35-12a的讨论
管 训 贵
(泰州学院 数学系, 江苏 泰州 225300)
关于丢番图方程X2-(a2+1)Y4=35-12a的讨论
管 训 贵
(泰州学院 数学系, 江苏 泰州 225300)
摘要:设a是正整数,证明了当a=1时,方程X2-(a2+1)Y4=35-12a仅有正整数解(X,Y)=(5,1);当a=2时,该方程仅有正整数解(X,Y)=(4,1)和(56,5);当a=3时,该方程仅有正整数解(X,Y)=(3,1);当a=4时,该方程仅有正整数解(X,Y)=(2,1)和(202,7);当a=5时,该方程仅有1组互素的正整数解(X,Y)=(1,1);当a=6时,该方程无正整数解(X,Y);当a≥7且12a+1为非平方数时,该方程最多有3组互素的正整数解(X,Y);当a≥7且12a+1为平方数时,该方程最多有4组互素的正整数解(X,Y).
关键词:四次方程;虚二次域;丢番图逼近;解数;上界
GUANXungui
(Department of Mathematics, Taizhou University, Taizhou 225300, Jiangsu Province, China)
0引言
设D,k是正整数且D无平方因子,方程
X2-DY4=-k
(1)
是一类基本而又重要的4次丢番图方程,其相关结果尚不多[1-6].
文献[1]在认真研究4次域的单位数后,证明了D=2,k=1时,方程(1)仅有正整数解(X,Y)=(1,1),(239,13);文献[2]用类似的方法证明了当D=5,k=4时,方程(1)仅有正整数解(X,Y)=(1,1).
本文利用超几何函数、代数的有效逼近和Pell方程解的性质给出了一般性的结果.
定理方程
X2-(a2+1)Y4=35-12a.
(2)
(i)当a=1时,仅有正整数解(X,Y)=(5,1);
(ii)当a=2时,仅有正整数解(X,Y)=(4,1)和(56,5);
(iii)当a=3时,仅有正整数解(X,Y)=(3,1);
(iv)当a=4时,仅有正整数解(X,Y)=(2,1)和(202,7);
(v)当a=5时,仅有1组互素的正整数解(X,Y)=(1,1);
(vi)当a=6时,无正整数解(X,Y);
(vii)当a≥7时,若12a+1为非平方数,则除(X,Y)=(a-6,1)外,最多还有2组互素的正整数解(X,Y);若12a+1为平方数,则除(X,Y)=(a-6,1)和(12a2+a+6,(12a+1)1/2)外,最多还有2组互素的正整数解(X,Y).
1超几何函数、代数数的有效逼近与若干引理
设α,β,γ为复数,且γ≠0或负整数.超几何函数F(α,β,γ)定义为复变量z的幂级数,即
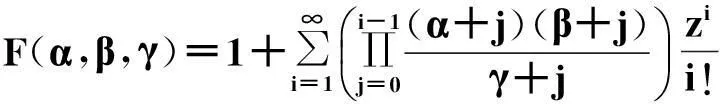
令r为正整数,v为实数且满足0 Yr(z)=F(-r-v,-r,1-v,z), Xr(z)=zrYr(z-1), 以及 这里积分路径不过0,并且当u=0时,有 (1-u)-r-1+v=1. 且C1,f为实数,满足0 (3) (4) (ii)若r0=1且η-1qB4,1≠pA4,1,η=±1,则 (iii)若r0=1且η qB4,1=PA4,1,η∈{±1,±i},则 (i) um+n=umun+Dvmvn,vm+n=umvn+unvm; 引理4[8]设D≥3是整数,则方程x2-Dy4=-1最多有一组正整数解(X,Y). 引理5[9]方程x2-5y4=11仅有正整数解(X,Y)=(4,1)和(56,5). 引理7[11]设pm/qm是无理数α的连分数展开式的第m个渐近分数.若e和f是互素的非0整数且存在正实数c,使得 则(e,f)=(rpm+1±spm;rqm+1±sqm),其中m是某些非负整数,r,s是正整数,满足rs<2c. 引理8设a≥7为整数,则方程 x2-(a2+1)y2=35-12a 的所有互素的整数解由 证明根据引理4(iii)和引理5可得. 引理9[6]设a≥7,若(X,Y)≠(a-6,1)为方程(2)的一组互素的正整数解,则 引理10设a≥7,若(X,Y)≠(a-6,1)为方程(2)的一组互素的正整数解,则有正整数x,y,g使得g2<12a-35且 (5) (6) 证明令g=min{b1,b2}.由gcd(b1,b2)=1,b1b2=12a-35≥49知,b1≠b2,故g2<12a-35. 当g=b1时,令x=b1r,y=-s;当g=b2时,令x=b2s,y=r.于是由引理9可得 即有式(5)成立,且满足式(6).引理10得证. 若 则 引理12设a≥7.若(X,Y)为方程(2)的一组互素的正整数解,Y2=T2k±(a-6)U2k,k>1,则 (i) k=2时,Y2>4(12a+1)a2,且 T4-(a-6)U4=48a3+4a2+24a+1, T4+(a-6)U4=16a4-48a3+12a2-24a+1; (ii) k=3时,Y2>4(48a3+4a2+48a+3)a2,且 T6-(a-6)U4=192a5+16a4+192a3+ 12a2+36a+1, T6+(a-6)U6=64a6-192a5+80a4-192a3+ 24a2-36a+1; (iii) k=4时,Y2>8(96a5+8a4+144a3+10a2+60a+3)a2,且 T8-(a-6)U8=768a7+64a6+1152a5+80a4+ 480a3+24a2+48a+1, T8+(a-6)U8=256a8-768a7+448a6-1152a5+ 240a4-480a3+40a2-48a+1; (iv) k≥5时,Y2>3072a9. 证明由递推关系,有 T2(k+1)=(2a2+1)T2k+2a(a2+1)U2k, U2(k+1)=2aT2k+(2a2+1)U2k. (7) T4=8a4+8a2+1,U4=8a3+4a. 此时结论成立. (ii) k=3时,由式(7)可得 T6=32a6+48a4+18a2+1,U6=32a5+32a3+6a. 此时结论成立. k=4和k≥5时,由式(7)同理可证得结论成立.根据引理10和引理11,类似文献[6]中引理3.9和引理3.11的证明方法,可得下述引理13和引理14. 引理13设a≥7,若(Xj,Yj),Yj>1(j=1,2,3)为方程(2)的3组互素的正整数解,则存在j1,j2∈{1,2,3}使得 引理14若(Xj,Yj)(j=1,2,3)为方程(2)满足 的3组互素的正整数解,则存在2组互素的正整数解,不妨设为(X1,Y1),(X2,Y2),Y2>Y1,使得η1/η2=±1,且 其中当kj=2时,a≥10;kj≥3时,a≥4. 2定理的证明 (i)当a=1时,方程(2)成为 X2-2Y4=23. (8) 首先考虑方程 a2-2b2=23. (9) 根据引理2,方程(9)的一般解可由以下2个非结合类给出: 或 若方程(8)有整数解,必存在n使得Y2=±(un+5vn)或Y2=±(un-5vn)=±(u-n+5v-n). 当n≥0时,un+5vn>0;当n<0时,un+5vn<0.因此可归结为 Y2=un+5vn,n≥0 (10) 或 Y2=-un+5vn,n>0. (11) 由引理3可得下列关系: un+2=6un+1-un,u0=1,u1=3; (12) un+2=6vn+1-vn,v0=0,v1=2; (13) v2x=2unvn; (14) un+2km≡(-1)kun(modum), vn+2km≡(-1)kvn(modum). (15) 对式(11)~(13)模8得剩余序列周期为4,且当n≡0,1,2,3(mod4)时,-un+5vn≡7,7,3,3(mod8)均为模8的平方非剩余,故式(11)不成立. 对式(10)~(13)模8得剩余序列周期为4,且当n≡1,2(mod4)时,un+5vn≡5,5(mod8)为模8的平方非剩余,故排除,剩n≡0,3(mod4). 对式(10)~(13)模3得剩余序列周期为4,且当n≡3(mod4)时,un+5vn≡2(mod3)为模3的平方非剩余,故排除,剩n≡0(mod4). 若n≠0,可设n=2s(2k+1),s≥2,则由式(10),(14)和(15)可知 Y2≡±(u2s+5v2s)(modu2s)≡ ±5v2s(modu2s). (16) 考虑到u2k≡1(mod8),令2t‖v2k,由式(16)可得 即 (17) 由于un模5的剩余序列周期为6,2S模6的剩余序列周期为2,故s=2,3.此时u2s≡2,2(mod5)为模5的平方非剩余.这说明式(17)不可能成立.因此n=0,可得方程(8)仅有正整数解(X,Y)=(5,1). (ii)当a=2时,方程(2)成为 X2-5Y4=11. (18) 由文献[6]知,方程(18)仅有正整数解(X,Y)=(4,1)和(56,5). (iii)当a=3时,方程(2)成为 X2-10Y4=-1. (19) 根据引理4,方程(19)仅有正整数解(X,Y)=(3,1). (iv)当a=4时,方程(2)成为 X2-17Y4=-13. (20) 仿(i)可证明方程(20)仅有正整数解(X,Y)=(2,1)和(202,7). (v)当a=5时,方程(2)成为 X2-26Y4=-25. (21) 仿(i)可证明方程(21)仅有1组互素的正整数解(X,Y)=(1,1). (vi)当a=6时,方程(2)成为 X2-37Y4=-37. (22) (vii)当a≥7时,假定(Xj,Yj)(j=1,2,3)为方程(2)3组互素的正整数解,满足 由Y1(ω)=F(-5/4,-1,3/4,ω)=1+5ω/3,X1(ω)=ωY1(ω-1)=ω+5/3,△4,1=3和N4,1=8,知 的正整数.以下分3种情形讨论. 因此, 由引理13知 故 情形2r0=1,ηqB4,1=pA4,1以及η∈{±1,±i}.此时 令gcd(X1,12a-35)=l,由gcd(X1,Y1)=1知 l|(a2+1),故l|12(a2+1)-a(12a-35)=35a+12,从而l|12(35a+12)-35(12a-35)=1 369.因此可推得 (23) 由式(23)及引理10可得 (24) 又由引理1(iii),知 于是, (25) 由g1g2<12a-35,并结合式(24)和(25)得 当a≥86时,与引理12矛盾.7≤a≤85的情况将在后面一并讨论. 情形3r0>1.由r0的定义知,ω2|qf|≥1,故 (26) (27) 根据引理14,结合式(27)和g1g2<12a-35,可得 (28) 若k≥5,则由a≥7知Y2>2 529 924 096a2,与式(28)矛盾,于是k=2或3或4. 若k=4,7≤a≤10,则可分别算出:T8-(a-6)U8=109·6 052 573,857·1 943 657,109·5431·6 379,18 731·419 651;T8+(a-6)U8=5·601·291 869,7·11·35 906 309,107·1 733·40 543,199·91 732 279.它们皆非平方数,故a≥11.此时Y2>126 172 488a2,亦与式(28)矛盾,于是k=2或3. 若k=3,7≤a≤86,则由Maple9.5计算可知,T6±(a-6)U6皆非平方数,故a≥87.此时Y2>126 570 396a2,仍与式(28)矛盾.于是k=2. 若k=2,7≤a≤2 603 192,则由Maple9.5计算可知,T4±(a-6)U4皆非平方数,故a≥2 603 193.此时Y2>124 953 268a2,同样与式(28)矛盾. 最后,讨论k=1的情形. 假定(X,Y)≠(a-6,1)为方程(2)的一组互素的正整数解,满足Y2=T2±(a-6)U2,则Y2=2a2+1±(a-6)·2a,故有Y2=4a2-12a+1及Y2=12a+1.前式解出a=3,与a≥7矛盾,后式对应的X=12a2+a+6. 定理得证. 注运用文中的方法还可以证明丢番图方程X2-(a2+1)Y4=k2-1-2ka在一定条件下最多只有2组互素的正整数解.限于篇幅,将另文介绍. 参考文献(References): [1]LJUNGGREN W. Zur theorie der Gleichungx2+1=Dy4[J].Avh Norsk Vid Akad Oslo,1942(5):1-27. [2]LJUNGGREN W. On the Diophantine equationAx4-By2=C(C=1,4)[J].Math Scand,1967,21(2):149-158. [3]袁平之,张中锋.丢番图方程X2-(a2+4p2n)Y4=-4p2n[J].数学学报:中文版,2014,57(2):209-222. YUAN Pingzi, ZHANG Zhongfeng. On the Diophantine equationX2-(a2+4p2n)Y4=-p2n[J]. Acta Mathematica Sinica: Chinese Series,2014,57(2):209-222. [4]STOLL M, WALSH P G, YUAN P Z. On the Diophantinc equationX2-(a2m+1)Y4=22m[J]. Acta Arith,2009,139(1):57-63. [5]YUAN P Z. Squares in Lehmer sequences and the Diophantine equationAx4-By2=2[J]. Acta Arith,2009,139(3):275-302. [6]YUAN P Z, ZHANG Z F. On the Diophantine equationX2-(1+a2)Y4=-2a[J]. Sci China: Ser A,2010,53(8):2143-2158. [7]柯召,孙琦.谈谈不定方程[M].上海:上海教育出版社,1980:30-31. KE Zhao, SUN Qi. On the Diophantine Equations[M]. Shanghai: Shanghai Education Press, 1980:30-31. [8]CHEN J H, VOUTIER P M. A complete solution of the Diophantine equationx2+1=dy4and a related family of quartic Thue equations[J]. J Number Theory,1997,62(1):71-99. [9]COHN J H E. Some quartic Diophantine equations[J]. Pacific J Math, 1968,26:233-243. [10]HUA L K, Introduction to Number Theory[M]. Translated by PETER S. Berlin, New York: Springer-Verlag,1982. [11]DUJELLA A, Continued fractions and RSA with small secret exponent[J]. Tatra Mt Math Publ,2004,29:101-112. [12]孙琦,袁平之.关于不定方程x4-Dy2=1的一个注记[J].四川大学学报:自然科学版,1997,34(3):265-268. SUN Qi, YUAN Pingzhi. On the Diophantine equationx4-Dy2=1[J]. Journal of Sichuan University: Natural Science Edition,1997,34(3):265-268. DiscussionontheDiophantineequationX2-(a2+1)Y4=35-12a.JournalofZhejiangUniversity(ScienceEdition), 2016,43(2):138-143 Abstract:Let a be an positive integer. We prove that if a=1, then the equation X2-(a2+1)Y4=35-12a has only one positive integer solution (X,Y)=(5,1); If a=2, then the equation has only two positive integer solutions, (X,Y)=(4,1) and (56,5); If a=3, then the equation has only one positive integer solution (X,Y)=(3,1); If a=4, then the equation has two positive integer solutions (X,Y)=(2,1) and (202,7); If a=5, then the equation has one coprime positive integer solution (X,Y)=(1,1); If a=6, then the equation has no positive integer solution (X,Y); If a≥7 and 12a+1 is a nonsquare positive integer, the equation has at most three coprime positive integer solutions; While if a≥7 and 12a+1 is a square, the equation has at most four coprime positive integer solutions. Key Words:quartic equations; imaginary quadratic fields; Diophantine approximations; number of positive integer solutions; upper bound 中图分类号:O 156.7 文献标志码:A 文章编号:1008-9497(2016)02-138-06 DOI:10.3785/j.issn.1008-9497.2016.02.003 作者简介:管训贵(1963-),ORCID:http://orcid.org/0000-0001-7612-2635,男,本科,教授,主要从事数论研究,E-mail:tzszgxg@126.com. 基金项目:江苏省教育科学“十二五”规划项目(D201301083);云南省教育厅科研项目(2014Y462);泰州学院教授基金项目(TZXY2015JBJJ002). 收稿日期:2015-06-01.