基于最小二乘法的暂培箱温度调控模型

孙祥+杨信廷+刘燕德+李莎

摘要： 为了对暂培箱温度进行更加合理的调控，设计1种探索性试验，通过向暂培箱注入热水来调节水温。在暂培箱初始水位相同，而外界温度不同时，通过向暂培箱内注入不同温度的水，观察其水温变化情况。通过最小二乘法拟合出温度变化的二次项模型和对数模型。2种模型在拟合中各有利弊，且暂培箱初始温度相近时可以用同一个模型表示。为了证明该模型能有效预测温度的变化情况，对其进行了验证试验。结果表明，可以利用有限个温度变化模型预测温度变化情况，为今后利用该方法获得的模型用于暂培箱温度调节打下了基础。

关键词： 暂培箱；温度调节模型；最小二乘法

中图分类号： S969.33 文献标志码： A 文章编号：1002-1302（2016）03-0426-05

在鱼的运输、酒店和超市销售鱼的过程中，都需要对鱼进行暂时的养殖，而观赏鱼鱼缸养殖也可作为暂养来对待。为了更好地对鱼进行暂养，其暂养环境必须要保证其正常活动。温度是影响鱼正常生长的关键因素，研究表面，低温会影响鱼摄食量和生长[1-2]。温度影响鱼的新陈代谢，从而影响鱼的正常活动[3-5]。必须要对温度进行调节，特别是对于家养观赏鱼。目前，对于温度温度的调节主要是升温调节，而升温调节中主要使用普通加热棒，而利用PID[比例（proportion）、积分（integral）、导数（derivative）]控制加热装置对温度进行调节相对而言控制更加准确。利用模糊控制加热装置对温度进行调节不需要建立复杂的数学模型，从而也有所应用[6]。而与传统的直接控制加热装置对暂培箱水温进行加热不同，本研究探讨1种通过向暂培箱内注入不同温度的水，对暂培箱水进行升温的方法，观察其温度变化情况，从而建立相关变化模型。

暂培箱在注水过程中的温度变化模型。根据传热学原理，热量的传递可分为热辐射、热对流和热传导[7]。所以暂培箱温度受环境温度、光照等影响，而在向暂培箱内注入水时，虽然主要是热对流，但其中也包括热传导。而且热传导分为稳态热传导和非稳态热传导。要想建立一个较为准确的数学模型是很难的，再加上热对流也非常复杂，只靠简单的模型很难准确表示其过程。，建立对象的数学模型可以采用解析法和测试法。解析法是通过分析其过程的机理来求取对象模型；而测试法是根据实际输入和输出的实测数据经过分析得出的模型。测试法不需要对过程进行详细了解，只需从输入输出上描述其动态特性。所以在这里采用试验的方法建立相关模型。

1 材料与方法

1.1 材料

通过向鱼缸内注入一定温度的水进行温度调节来观察其温度变化过程，材料包括：长60 cm、宽60 cm、高80 cm的鱼缸、温度记录仪、液位记录仪、水泵、软管、加热装置、水箱等。为了在不同外部环境温度下进行试验，试验在日光温室内进行。方法为在不同室温时，鱼缸水温也不同，通过向鱼缸中注入一定温度的水观察温度变化情况。本试验中外界温度选择分别为16、20、25、30 ℃，注入水的温度为30、35、40 ℃。

1.2 方法

以外界环境温度为16 ℃时进行温度调控的过程。首先让鱼缸内水位保持在一定值，即对一定量的水进行调控。然后将30 ℃的水注入浴缸内，观察温度的变化和水位。待环境温度、鱼缸水位、鱼缸水温都与30 ℃水进行试验前一致时进行35 ℃水的试验，通过恢复到初始值时进行40 ℃水的试验。

因为每次试验鱼缸温度都产生变化，为了试验的准确性，使外界温度和初始鱼缸水位与水温都保持一致，试验分多次进行，剔除不符合条件的试验。这样反复进行试验最后得到较为准确的试验值。

2 结果与分析

2.1 不同外界温度条件下鱼缸水温度变化

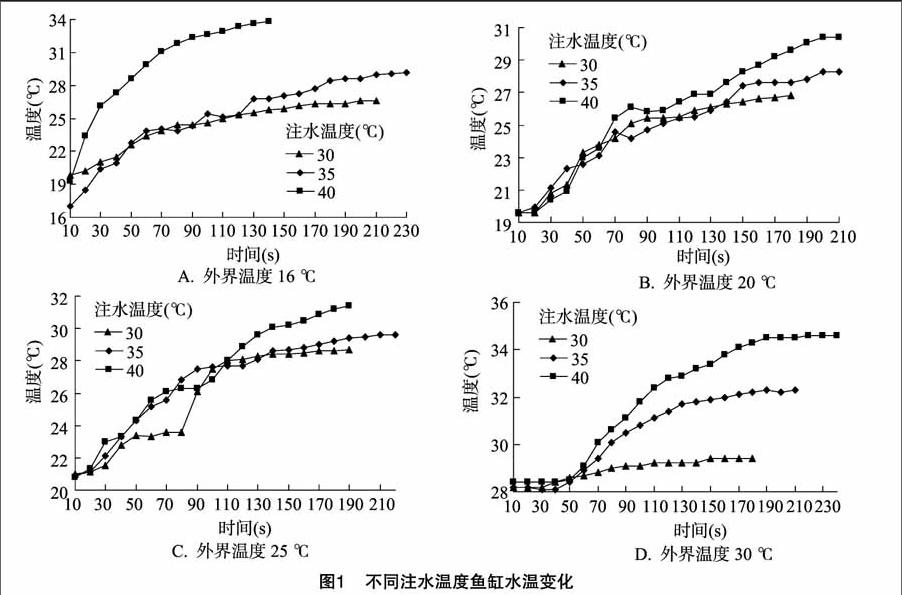
从图1-A可以看出，当外界温度为16 ℃进行试验时，3条曲线都是先快速上升，然后慢慢趋于平行。因初始鱼缸水位和水温都一样，所以因注入水的温度不同而不同；在刚开始注入水时其温度变化速率不同；30 ℃的水温度始终缓慢增长，其增长曲线接近直线；而35 ℃的水开始快速增长，但很快又缓慢增长，其增长速率比30 ℃的水稍快，但后续也接近平行。相对30、35 ℃的水，40 ℃的水变化较为特殊，30 ℃的水和35 ℃的水变化曲线非常接近，而40 ℃的水变化非常快速，且变化幅度大，其增长曲线接近对数增长形式。从开始1 min来看，30 ℃水时温度增加了4 ℃，35 ℃水时温度增加了6 ℃，而40 ℃水增加了11 ℃。

从图1-B可以看出，当外界温度为20 ℃进行试验时，3条温度变化曲线的总体变化趋势与16 ℃时相同，先快速增长，后趋于平缓，但不同的是3条曲线变化基本相同，不同于16 ℃时40 ℃的水温度变化更迅速，在1 min内基本相同增加了4 ℃，之后40 ℃的水温度开始升高然后趋于平缓，但始终高于30、35 ℃水。30、35 ℃的水温度变化在140 s后开始出现分离，35 ℃水继续缓慢增长，而30 ℃水增长更为缓慢。

从图1-C可以看出，当外界温度为25 ℃进行试验时，3条曲线总体上也是先快速增长然后趋于平缓，但3条曲线都出现了先快速增长然后平缓后又快速增长的过程，注入30 ℃水时表现尤为明显，35 ℃水次之。在40～100 s之间30 ℃的曲线相对于另外2条曲线表现较为反常。1 min内30 ℃的水温度增加3 ℃，而35～40 ℃的水增加5 ℃。在试验100 s后30、35 ℃的曲线基本相同，而40 ℃的曲线继续快速增长。

从图1-D可以看出，当外界温度为30 ℃进行试验时，35、40 ℃的曲线为先快速增长，然后趋于平缓，而30 ℃的曲线一直缓慢增长，这可能是由于鱼缸本身温度较高的原因。从图中可以看出3条曲线相差较大，在处理120 s时，30 ℃水温度增加1 ℃，35 ℃水温度增加3 ℃，而40 ℃水使温度增加5 ℃。

2.2 注水温度相同、外界温度不同时鱼缸水温度变化

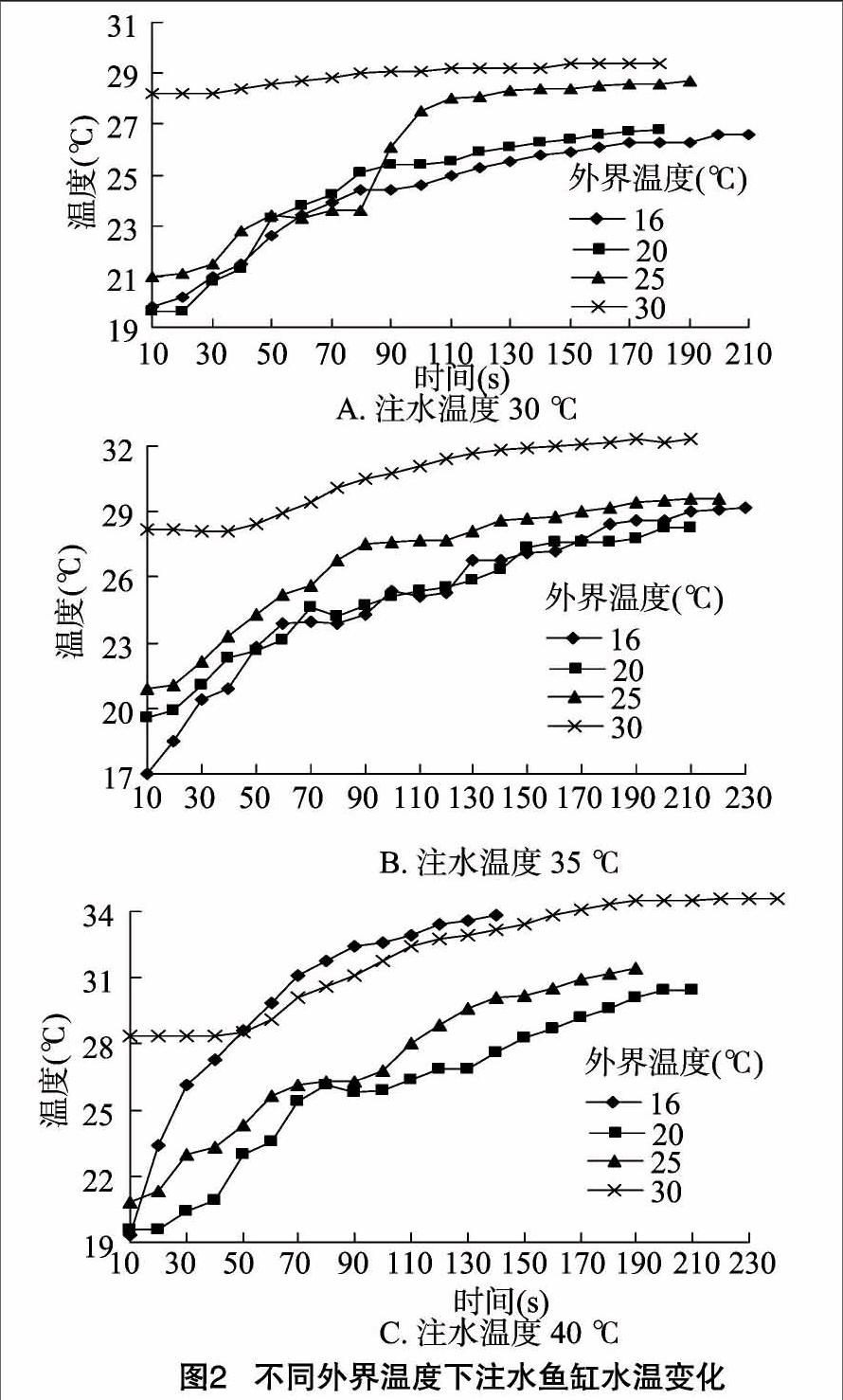
从图2-A可以看出4种外界温度下，注入30 ℃水时温度的变化。因外界温度不同所以各个温度下鱼缸内水的初始温度会有所差异，外界温度为30 ℃时差异明显。前80 s内，16、20、25 ℃ 3条曲线基本相同，但80 s后16、20 ℃基本相同，而25 ℃开始快速增长且偏离16、20 ℃曲线较大。而相对前3条曲线，40 ℃的曲线一直缓慢增长，曲线接近直线。

从图2-B的温度变化曲线可以看出，外界温度为16、20 ℃ 时的温度变化曲线基本相同；而25 ℃的外界温度时的曲线略高于16、20 ℃时的曲线，但最终温度与16、20 ℃时基本相同；外界温度为30 ℃时，相对于前3种温度，其曲线更趋于平缓，温度增长较小，但鱼缸水温明显高于前3种温度。

从图2-C可以看出，4条曲线并无重合，其中20 ℃外界温度时鱼缸温度变化最低，25 ℃外界温度时次之，16 ℃外界温度时，鱼缸温度变化明显且变化较为迅速，在开始1 min后超过了30 ℃的曲线。

2.3 最小二乘法曲线方程拟合

为了将试验所得结果更好地指导实际中温度的控制调节，最好可以得到温度调控的数学模型。通过前面的分析我们可以知道，注入流量相同，而外界温度的不同、鱼缸初始温度的不同，即使是相同的注水温度其结果也会不同。图3为所有试验过程中水深和温度变化，无法用单一曲线对其情况进行描述。从图4可以看出整个试验过程中鱼缸水位基本呈线性增长，可以用1条曲线计算出其变化过程。水位变化相同也就说明流量相同，这样可以在1副图中对温度变化进行描述。

本试验中利用最小二乘法对曲线进行拟合并求出近似方程，下面对最小二乘法进行简单介绍。假设在区间[a，b]上存在n个线性无关的连续函数φ0（x），φ1（x），…，φn-1（x），离散函数f（x）在区间[a，b]上存在n个节点满足a=x1

式中：ωi为权数，其值大于零[8-9]。

最小二乘法一般常用在多变量拟合和曲线拟合中，所谓多变量式拟合就是利用最小二乘式Q（x）=c0+c1x+Λ+cn-1xn-1区去逼近f（x）。其中：当n=2时为直线拟合。在实际中非线性曲线比直线出现的频率要高得多，但某些非线性问题可以转换为线性问题来进行求解，下面介绍经常出现的一种非线性情况。

实际中曲线y=c0ec1x经常碰到，若直接利用最小二乘法对∑k i=1[yi-c0ec1x]2进行最小化求解，因会出现c0、c1的非线性方程，所以很难求解。通常采用两边取对数的方法进行线性化，可得lny=lnc0+c1x，令z=lny，s=lnc0，可得z=s+c1x，然后再利用最小二乘法求得s、c1，再求出c0，最后求出方程。

首先对鱼缸水位的增长曲线进行拟合，从图4可以看出，水位随时间变化的曲线接近一条直线，且几条曲线基本重合。求得各时间点温度的平均值，利用平均值进行直线的拟合，设x为时间，y为鱼缸水位，求得x与y的相关判定系数，r2=0998，可见相关性很强。设直线方程为y=ax+b，利用最小二乘法求得直线方程为：

式中：31.489表示初始鱼缸水位，斜率4.450 6表示单位时间内注入水的流量，拟合过程中误差平方和为r2=44.556 9。散点图和拟合直线见图5。

从上述分析可知，室温和注水温度不同鱼缸水温的变化曲线不同，其中室温不同若鱼缸水温近似时，变化曲线相差不大。可见影响鱼缸水温变化的主要是鱼缸初始水温和注水温度。从上述分析还可知，鱼缸水温初始值相差不大时注水温度相同，变化曲线近似，这样可以用初始水温为20 ℃的曲线近似表示18、22 ℃，28 ℃的初始温度曲线近似代表26、30 ℃，下面求初始温度为20、28 ℃，注入水温为30、35、40 ℃时的温度变化曲线。

从变化曲线来看，可以用二次多项式或非线性函数y=blnax表示，下面对其进行拟合求解。初始温度为20 ℃，注水温度为30、35、40 ℃时的温度变化二次多项式函数和对数函数见表1、表2，拟合曲线见图6、图7；初始温度为28 ℃，注水温度为30、35、40 ℃时的温度变化二次多项式函数和对数函数见表3、表4，拟合曲线见图8、图9。

从表1至表4可以看出，二次多项式的拟合曲线和对数方程的拟合曲线相比较，最大误差和均方根误差均较小，但从图6至图9中可以看出，曲线在开始时均方根误差较大，而最后二次项曲线有下降趋势，对数曲线有逐渐平缓趋势。相对二次项曲线，对数曲线更与实际温度变化曲线相类似。从图6至图9还可以看出，曲线在温度开始上升和逐渐平缓时可以适用，而当开始温度变化不明显和最后平缓后曲线不适用。表明方程的自变量时间的取值必须在一定范围内。

2.4 模型验证

对方程进行验证，选择初始水温为20 ℃、注水温度为35 ℃的方程进行验证。通过试验获取初始水温为20 ℃、注水为35 ℃的数据，将其与方程计算结果相比较，结果见图10。其中二次项方程最大误差为2.862 9，均方根误差为1.163 7，对数方程最大误差为3.596 4，均方根误差为1.076 6。从均方根误差可以看出，2种方程误差都较小，可以用来进行预测分析。通过试验对其他方程进行验证也都满足要求。

3 讨论与结论

通过试验，探索在暂培箱水位相同的情况下，在不同外界温度下，向暂培箱内注入不同温度的水，观察暂培箱温度变化情况，并利用最小二乘法拟合温度变化的2种不同方程。研究发现，在温度调节过程中，外界温度对水温的变化基本没有影响，当暂培箱内水位相同、初始水温相同时，温度变化曲线基本相同。而在水位相同、初始水温相差2 ℃以内时，温度变化曲线也基本相同。

对于拟合的二次项方程和对数方程，可以看出二次项方程的误差较小，但对数曲线变化趋向比二次项趋向更接近真实情况。通过上述模型我们可以直接对暂培箱水温进行调控，也可以与一些控制算法相结合，使水温调节更加高效、准确和节能。

参考文献：

[1]Hochachka P W，Somero G N. Biochemical adaptation：mechanism and processing physiological evolution[M]. New York：Oxford University Press，2002：466.

[2]Xie X J，Sun R Y. The bioenergetics of the southern catfish（Silurus meridonalis Chen）：growth rate as a function of ration level，body weight and temperature[J]. Journal of Fish Biology，1992，40（5）：719-730.

[3]冯广朋，庄 平，章龙珍，等. 温度对中华鲟幼鱼代谢酶和抗氧化酶活性的影响[J]. 水生生物学报，2012，36（1）：137-142.

[4]鲜雪梅，曹振东，付世建. 驯化温度与急性变温对南方鲇幼鱼皮肤呼吸代谢的影响[J]. 生态学报，2013，33（8）：2444-2451.

[5]徐革锋，王裕玉，韩 英，等. 不同温度条件下运动和摄食对细鳞鲑幼鱼代谢模式的影响[J]. 应用生态学报，2014，25（4）：1156-1162.

[6]吴 渊. 基于模糊PID的循环水温度控制系统研究[D]. 成都：电子科技大学，2013：15-26.

[7]杨世铭，陶文铨. 传热学[M]. 4版.北京：高等教育出版社，2006.