巧铺路，精提炼，为学生打开立体几何学习之门

吕玲

中图分类号：G623.5 文献标识码：A 收稿日期：2015-12-23

1.夯实基础，透彻理解基本概念

很多学生认为，只有在单纯的理论学习中，才需要特别关注基本概念。立体几何十分具体，便无须对较为虚化的数学概念过于关注，其实这是学生学习立体几何的一个重大误区。在对立体几何的内容进行灵活理解与应用的过程中，掌握基本概念是前提。只有这样，学生才能明确立体几何中的每一个元素以及每一种位置关系，这对空间关系的搭建会起到至关重要的作用。

例如，在学习过正三棱锥的概念之后，我要求学生试着解答这样一个问题：图1是一个正三棱锥P-ABC的主视图，若AC=BC=—，PC=√6，则该正三棱锥的全面积是多少？想要顺利回答这个问题，就要把已知条件用足，透彻理解基本概念就显得尤为重要了。对于正三棱锥来讲，何为“正”？学生们必须知道它的顶点在底面上的射影是底面正三角形的中心就是三棱锥，才可以由题目条件得知，主视图的投影方向是面对这个正三棱锥的一条侧棱，且与底面三角形的一条边垂直，各棱长随之可求。

由此可知，夯实基础对于立体几何的有效学习具有重要的推动作用。教师必须认识到这一点，并在教学过程中予以实践。

2.丰富形式，构建空间想象能力

想要学好立体几何，就要有丰富的空间想象能力，而这个能力的培养，并不是仅靠学生自身的单一学习就可以达成的。空间想象能力是一种比较特殊的感性认知，需要走出惯常的平面思维来达成。它不是自发出现的，需要教师通过对外部因素进行调整来激发其形成。这就对教学形式的多样化提出了更高的要求。

例如，在实际教学中，学生总反映对一些立体图形自己就是看不出它的立体感觉，或者只能从某个典型的特定角度才能分析出它们的空间感。这就是空间想象能力不足的表现。为此，笔者跳出了固有的坐标系教学思维，采用多视角视图的形式展现立体几何图形，让学生得以从全新的角度来感受图形的空间感。笔者曾经要求学生观察图2中一组几何体的三视图，并通过图中所标示出的数据来求得这个几何体的表面积。这样的思考方式让学生眼前一亮：第一次尝试以既实际又多维的方式来看待一个几何体。起初，大家在还原该几何体的过程中虽然存在一些操作困难，但思考结束后，空间想象能力得到了快速提升。

现代技术手段的进步与教学思维的拓展，也为立体几何教学提供了更为丰富的方式选择。更多教学方式的出现，不仅让高中数学课堂充满了新鲜感，也从多角度打开了学生思维，为其空间想象能力的构建铺平了道路。

3.大胆探究，有效深化教学效果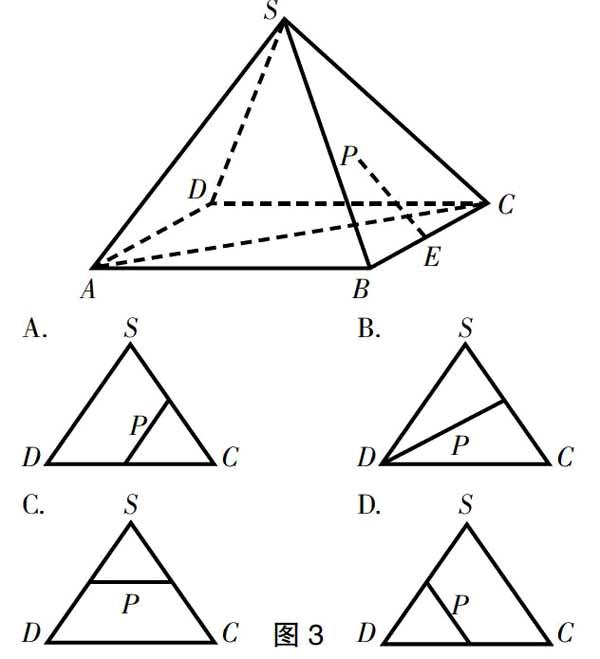

数学知识是灵活多变的，这一点在立体几何当中体现得尤为明显。在立体空间当中，留给学生的可能性更多。这虽然会让很多学生感到难以把握，但若能够对其加以巧妙运用，并抓住关键部分大胆探究，便可以成为立体几何学习效果深化与升华的关键入口。例如，我在课堂上向学生呈现过这样一道习题：如图3所示，点E是正四棱锥S-ABCD中边BC的中点，点P在侧面CDS内及其边界上运动，且总保持PE与AC垂直，则点P的轨迹与面CDS所组成的图形是A、B、C、D四幅图中的哪一个？这是一个以动点为主体的探究问题，具有很大的思考价值。对这个问题的探究，不仅有利于学生对正四棱锥基本概念的准确把握，还结合了对异面直线间以及点、线、面间的位置关系的透彻理解。完成这次探究，可以达成多个立体几何知识内容学习的协同升华。

显然，对立体几何知识的学习其实并没有想象中的那么困难。在笔者看来，立体几何的教学难点常常集中在入门之时。教师只要能够在学生刚接触相关知识内容时，将他们的学习思维引导至正确的轨道上，学生便会发现立体几何学习的乐趣所在，并在自发的学习动力之下，对立体几何内容的探究进行得愈发完整和深远。