浅论数学课堂中探究式学习的途径

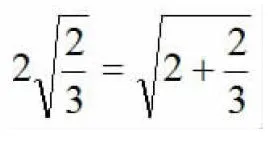
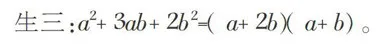
摘 " 要

培养学生自主探究能力是初中教学改革的一个重点。本文从学生兴趣、质疑、比较、实践和归纳总结等方面入手阐述了培养学生探究能力的若干途径。

关键词

自主探究 "教学改革 "质疑

培养学生自主探究能力是初中教学改革的一个重点。探究教学模式强调以学生为中心，要求教师由知识的传授者、灌输者转变为帮助学生主动学习的促进者。那么，怎样才能使探究式学习落到实处呢？在新课程教学的实践和探索中，笔者体会到可以从以下几方面着手：

一、在兴趣中探究

作为教师，在课堂上应给学生创设学习情境，让学生体验到学习的快乐，以积极主动的心理去获取知识。教学情境要体现数学知识和思想方法，只有当创设的教学情境进入学生认知的“最近发展区”，在内容上富有挑战性和探索性时，学生才能在已有认知水平的基础上，通过教师的适当引导，从中发现问题，提出问题，并形成解决问题的愿望。问题也可以在预习的基础上，由学生自己提出，以调动学生积极主动的学习心态。教师在创设问题情境时，还需注意问题的诱发性、生活性。

诱发性是指能激活学生的思维兴奋点，能够接近学生的认知水平与理解能力。生活性是指数学知识来源于生活，使数学知识生活化、浅显化。教师要充分挖掘教材因素，问题的设计要有针对性、启发性、趣味性、层次性，比较困难的问题，可以组织学生分组讨论。

比如，在复习一次函数时，笔者提了这样一个问题：“我”去购物，甲商场提出的优惠销售方法是所有商品按九五折销售，而乙商场提出的优惠方法是凡一次购满1000元可领取九折贵宾卡。请同学们帮老师出出主意，“我”到哪家商场购物得到的优惠更多？问题提出后，学生十分感兴趣，纷纷议论，连平时数学成绩较差的学生也跃跃欲试。学生学习的主动性很好地调动了起来。

二、在质疑中探究

从学生的好奇、好问、好动、求知欲旺盛等特点出发，积极鼓励学生敢于、善于提出问题，勤于思考问题，这是引导学生自主探究、培养学生创新意识的重要途径。教师要转变观念，改变“教师提问——学生回答”的教学模式，鼓励学生别出心裁、标新立异。在平时的教学中，教师要鼓励学生质疑，为学生搭建有效平台，引导学生自主探究。

例如，在学习了两个三角形全等的条件后，笔者出了这样一道判断题：两边及其中一边的对角对应相等的两个三角形全等。类似于“SAS”，我们把这个命题叫做“SSA”，是个假命题，通常教师利用等腰三角形构造反例来说明。课堂上有一学生问道：“边边角”还有成立的可能吗？沉寂了片刻后，班里的数学课代表举手说：我们学过的“HL”不就是属于“SSA”吗？老师当即表扬了这位学生，实际上，三角形全等的判定方法中，“HL”就是“SSA”成立的一个特例。没想到班里几个爱动脑筋的学生利用课余时间分析了“边边角”成立的条件，发现：1.当相等的角为直角时，“边边角”显然成立;2.当相等的角为钝角时，“边边角”也成立……通过探究学习，学生不仅体验到了成功的喜悦，而且激发了学习热情。

三、在比较中探究

比较是一切思维和理解的基础，人类是通过观察和比较来认识和了解事物的。数学教学实践证明，比较探究能够较好地刺激学生的学习内需，有助于学生深刻理解知识间的联系和区别，有效突破教学难点，促进数学知识的自主建构，提高思维的深度、广度和灵活度。

例如，在教梯形的概念时，笔者先让学生观察几幅日常生活中常见的梯子、跳箱和堤坝的横断面的图片，让学生找出这里面包含的相同图形。学生当即回答：梯形（小学里已接触到梯形）。

师：对！那你们可否给梯形定义？

生一：一组对边平行的四边形是梯形。

生二：老师，刚才那位同学说的一组对边平行的四边形不一定是梯形。因为只知道一组对边平行，那么另一组对边平行与不平行都有可能，所以这样的四边形可能是平行四边形也可能是梯形。因此，一组对边平行，另一组对边不平行的四边形才是梯形。

生三：一组对边平行且不相等的四边形是梯形。

学生们七嘴八舌，把关键的地方都一一找出来了。在此基础上笔者再让学生翻开书本，比较与书本的定义有何异同。经过师生的一番对话互动，学生对知识的理解更透彻，掌握更牢固，而且思维能力得到了锻炼，也感受到了数学的魅力。

四、在动手操作中探究

随着新课改的不断深入，教材中设计了许多实例和研究性课题，以鼓励和培养学生的创新意识和自主探究能力。在数学教学中，合理地、创造性地使用好教材，重视教学活动、数学实验的挖掘，对提升学生的素质无疑是大有裨益的。

例如，在整式乘法与因式分解这一章后面有一个关于拼图、公式方面的数学活动。

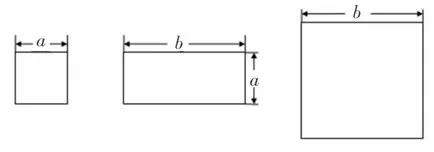
活动材料：若干块如图所示的长方形和正方形硬纸片。

活动要求：用若干块这样的长方形和正方形硬纸片，拼成一个新的长方形，通过不同的方法计算面积，探求相应的等式。

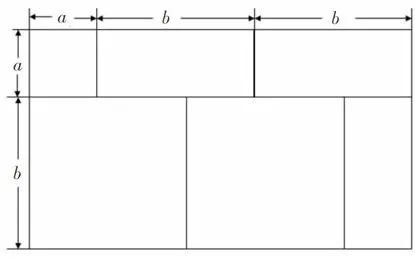
笔者事先将学生分成若干小组，以小组为单位进行探讨。学生们讨论片刻后，由每个小组派一名代表上台展示。其中，小明拼成的长方形如下图。

笔者：请同学们计算此长方形的面积。

生一：由于这个长方形是由六张卡片拼成的，所以它的面积就是这六张卡片的面积之和，故长方形的面积为a2+3ab+2b2。

生二： 长方形的面积公式是长乘宽，故这个长方形的面积也可表示为（a+2b）（a+b）。

师：两位同学都回答得非常好，（乘机追问）由此我们可以得到怎样的等式呢？

生三：a2+3ab+2b2=（a+2b）（a+b）。

师：对！请这位同学说说这个等式的代数意义？

生三继续回答：它表示多项式的因式分解。

（这时班级里又有不少同学举手）

生四：也可以得到这样的等式：（a+2b）·（a+b）=a2+3ab+2b2，它表示整式乘法。

教师见机又问：你能借助拼图的方法将二次三项式a2+4ab+3b2因式分解吗？最后，教师又追问：“如果任意写一个关于a、b的二次三项式，能否用若干块准备好的硬纸片拼成一个长方形，使这个长方形的面积可以用这个式子表示？如不能，你认为具备什么形式的二次三项式可以表示一个长方形的面积？” （这时同学们的探究热情高涨了起来）

整式乘法和因式分解是具有互逆关系的两种变形，好多学生感到整式乘法学起来容易一点，而因式分解就困难得多。这个课堂练习既促进了学生对知识与方法的运用，深化了知识间的联系，同时也激发了学生探究知识的兴趣，使他们体会到数形结合的魅力和功效。

五、在归纳总结中探究

在当今时代，知识不断更新，以知识占有为终极目的的教学已经不能适应时代发展的需求。教学不仅要让学生获得基础知识和基本技能，而且要让学生学习科学的探索方法，以培养学生主动探究发现知识的能力。教师要鼓励学生大胆运用类比、归纳、猜想、特殊化、一般化等方法去寻找解题策略，在经历“猜想—验证”“操作—发现”“观察—归纳”等探究发现的过程中掌握探究的方法。

例如，观察下列各式及其验证过程：

验证：

验证：

（1）按照上述两个等式及其验证过程的基本思路，猜想4的变形结果，并进行验证。

（2）针对上述各式反映的规律，写出用 n（n为正整数，n≥2）表示的式子，并给出证明。

通过认真观察，学生们会很快就猜想出4=，并得到验证，他们进一步注意到已知等式中的式子均由两个不同的数字构成，并且较大数字都是较小数字的平方减1，从而第二问也迎刃而解，最后得出规律：n=（n为正整数，n≥2）。通过对这一题的探究、引申推广，学生们受益匪浅。

总之， 在数学课堂教学中， 教师要把促进学生自主探究、主动发展， 培养实践创新能力放在首要位置， 善于为学生创设自主探究的情境， 激发学生自主探究的欲望， 由“要我学” 的被动学习转化为“我要学”“我爱学” 的自主探究学习，提高学生的自主探究和创造性思维能力，让学生真正成为数学学习的主人。

（作者为江苏省无锡市张泾中学教师）