还原课堂本真 追求实效高能

一、头脑风暴——百花齐放才是春

背景：本题是某区数学期中试卷上第28题，其第二问的难度不大，但是计算量较大，使得很多学生望题生畏，不敢尝试。

案例1 原题呈现：在平行四边形ABOC中，AO⊥BO，且AO=BO。以AO、BO所在直线为坐标轴建立如图1所示的平面直角坐标系，已知B（-6，0），直线y=3x+b过点C且与x轴交于点D。

（1）求点D的坐标；

（2）点E为y轴正半轴上一点，当∠BED=45°时，求直线EC的解析式。

图1

说明：对于第一小题，大部分学生能自己解决，但是在做第二小题时，学生对于条件“∠BED=45°”不知如何下手，只是知道这个45°肯定要起到意想不到的作用，可是45°有何用，让学生进入了思考。

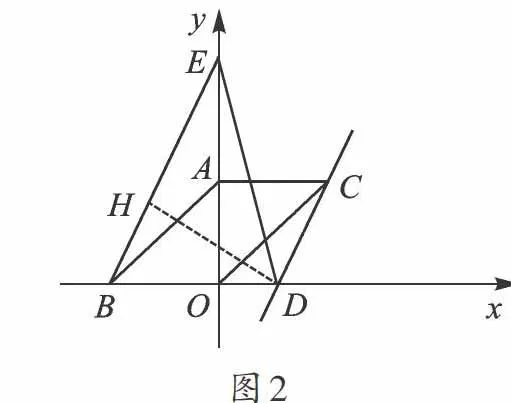
生1：这个45°不能破坏，最好能放在直角三角形中，故过点D向BE作高，构造直角三角形。如图2过D作DH⊥BE，设E点坐标为（0，t），则BE=[36+t2]，BD=10，ED=[16+t2]，由面积法可得：[12]DH·BE=[12]BD·OE，则DH=[10t36+t2]，当∠BED=45°时，[2]DH=ED，[2]·[10t36+t2]=[16+t2]，[100t236+t2]=[16+t22]，[t2]=144或4，则t=±12或±2，则t=12，即E点坐标为（0，12）。

图2

师：刚才这位同学用三角形的面积法求出了DH，进而利用∠BED=45°，发现△EHD为等腰直角三角形，DH∶ED=1∶[2]，找到等量关系。

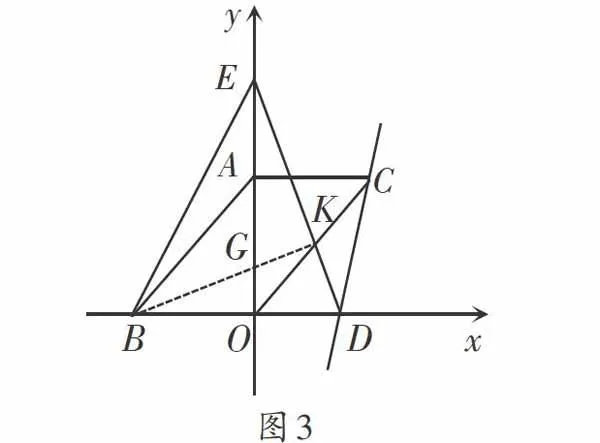
图3

生2：我也是将45°放在直角三角形中，我是过点B作BK⊥DE，交AO于点G，如图3，易得△EBK是等腰直角三角形，EK=BK，且易得∠BEO=∠OED=∠KBD，进而得到△EGK≌△BDK，EG=BD=10，再由tan∠KBD = tan∠OED得

[GOBO]=[ODEO]，[GO6]=[410+GO]，

GO=2或-12，OE=12。

师：同样是将45°角放入直角三角形中，同样也是作高，但这位同学得到等腰直角三角形后，想到相等的边，进而想到了三角形全等，再用反A型相似，得到了GO，将EO的长度转化成了EG与GO两段，分别进行求解，其计算量降低了不少，是个非常不错的解题思路。

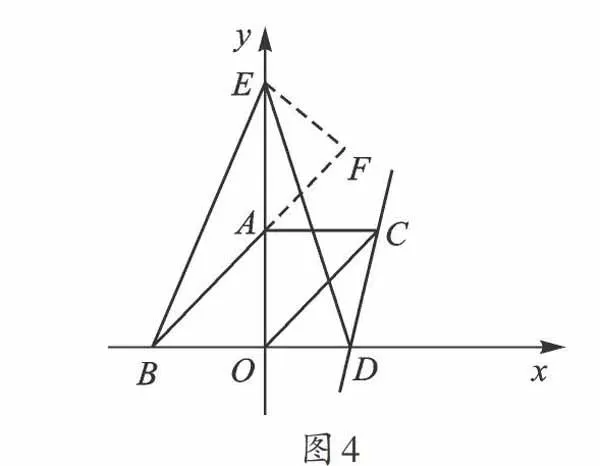
生3：我发现题中∠ABO=∠BED=45°，则∠BEO=∠OED，我就想试着用相似来解决。

图4

如图4，延长BA，过E作EF⊥BA，设AE=a，由∠BED=45°=∠ABD，则∠BEO=∠OED，∠BFE=∠EOD=90°，则△EBF ∽△DEO，[EFOD]=[BFEO]（或tan∠FBE= tan∠OED），由题意，EF=[22]a，FB=[22]a+6[2]，则[46+a]=[22a22a+62]，则a=-8或6，则E点坐标为（0，12）。

师：这种做法，利用了角度之间的转化，得到角相等，利用相似三角形（相等角的三角函数值相等）找到等量关系。相对而言，这个方程大家是会解的，只是面对这样的方程，等式的右边，分子分母上都是分数，计算很不方便，怎么办呢？

生齐：将等式右边的分子分母同时乘[2]这样计算就方便多了。

生4：老师说过，当代数的方法解决一个问题较复杂的时候，我们可以引进圆来试试，若这个45°当成圆的一个圆心角，则这个以45°为圆心角的等腰三角形底角为67.5°，且其同弧所对的圆周角为22.5°，这两个角不具有特殊性。故这种想法不合适。

若将45°构成一个圆的圆周角，则同弧所对的圆心角为90度。这个角度较特殊，可以尝试一下。

图5

如图5，∠BED=45°，若将∠BED当作一个圆周角，那么该圆的圆心角为90°。

则易得圆心为BD中垂线与BA的交点N，半径为5[2]，则易得Rt△EMN中，EN=5[2]，MN=1，则EM=7，即EA=6，OE=12，从而得E（0，12）

师：此法是借助△EBD的外接圆来进行解答，其方法相对来说最简单，但难点在于此圆的构造，不是一般同学能想到的，正如这位同学所说，当感觉面对45°这种特殊角，想用却用不起来时，不妨构造外接圆，尝试一下，可能会有意想不到的收获。

二、抓本质——拨开云雾见青天

背景：《一元二次方程》配方法第2课时，二次项系数不为1的一元二次方程如何求解。

案例2 教师在带领学生回顾完隔天所学的二次项系数为1的一元二次方程的解答步骤后，又练习了3个方程。x2-4x-3=0，x2-[83]x=1，x2-99=2x（这三个方程，类型包含带分数的，还有方程要先整理后再求解的）。学生求解，个别学生板演，教师批阅点拨后。教师顺势抛出了方程3x2-6x-1=0。

师：这个方程，同学们会解吗？

生齐：不会。

师：这方程与昨天的方程有何区别？

生齐：这方程二次项系数不是1。

师：怎么把二次项系数化为1呢？

生：两边同时除以3。

师：两边同时除以3后，新的方程是怎么样的？

生：x2-2x-[13]=0。

师：在除的过程中要注意什么？

生：每一项都要除以3。

师：这个方程你会解了吗？

……

大部分学生开始用隔天所学的方法开始解题……

突然有一个学生偷偷地，轻声地问他的同桌，为什么要除以3？

分析：这是一个真实的课堂情境，提这个问题的孩子数学基础不是很好，他问这个问题时，上课教师并没有发现，而笔者听课时正好坐在他的右边，故听到了这个不同的声音。面对这个孩子的提问，大部分教师会觉得很惊讶，理所当然地认为，其目的就是为了把二次项系数化为1呀？但是为什么要把系数化为1，老师没有将原因很好地告诉学生。其实，其真正原因是：学生隔天学会了二次项系数为1的方程用配方法来求解，当二次项系数不为1时，要想办法把不会解的方程化为会解的方程类型，即把未知转化为已知，所以要把二次项系数化为1……

我们的数学课堂，不仅要让学生知其然，更要让学生知其所以然，故在新授课时，不光要讲解方法，更应该跟学生讲清数学思想，从而让学生更好地理解数学，学好数学。

三、思辨——此时无声胜有声

背景：通过对前面知识的学习，学生已掌握了全等三角形定义及性质，对将要学习的三角形全等判定——“边角边”（SAS）有了一定的认识，现需探究“两条边相等，一对角相等的两个三角形全等”。

案例3 教师在回顾了全等三角形的定义及判定1后，问：两条边相等，一对角相等的两个三角形全等吗？

学生有的认为这两个三角形全等，有的认为这两个三角形不全等，但又不知如何举出反例。

只见教师拿出两张完全重合的三角形纸片，如图6，△ABC与△DEF，显然△ABC≌△DEF。

教师拿起△ABC纸片，将△ABC折叠，使得点C落在BC边上，记为点C'，如图7，然后让学生观察：△ABC'与△DEF中，ED=AB，DF=AC'，∠B=∠E，但△ABC'与△DEF全等吗？

分析：本节课主要采用引探式教学方法，在活动中教师着眼于“引”，尽力激发学生求知的欲望，学生着眼于“探”，通过观察与思考，感悟两边及一角相等，但是这两个图形不全等，进而挖掘出其全等的本质，两边及夹角分别对应相等，让学生更加深刻地理解夹角相等的重要性。这样的设计过程中，教师的话语不多，却胜在无声胜有声，润生细无声。

有效的数学课堂，定是能让学生“问得出问题”“说得出理由”“经得起实践”的课堂。只有还原本真课堂，抓住学生思维的火花，让星星之火燎原，向着课堂的深处，广处发展；我们更要抓住知识点的本质，让学生知道知识的“来龙去脉”，进而更好地建构知识框架；我们还要让学生学会“思辨”，学会用一分为二的眼光来观察数学，分析数学，进而更好地发现数学之美，数学之真谛！

（作者为江苏省无锡市旺庄中学教师）