PQ-树断点距离中心问题的复杂性和精确算法

刘培霞　姜海涛　朱大铭

(山东大学计算机科学与技术学院　济南　250101)

(liupeixia0629@163.com)



PQ-树断点距离中心问题的复杂性和精确算法

刘培霞姜海涛朱大铭

(山东大学计算机科学与技术学院济南250101)

(liupeixia0629@163.com)

Complexity and Algorithm for Minimum Breakpoint Median from PQ-trees

Liu Peixia, Jiang Haitao, and Zhu Daming

(ShoolofComputerScienceandTechnology,ShandongUniversity,Jinan250101)

AbstractA PQ-tree is a tree-based data structure which can represent large sets of permutations. Although the uncertainty of complete ancestral genomes is known, the homologous species provide information to determine the relative locations of partial genomes, whereby the PQ-tree can be designed to efficiently store ancestral genomes. In evolutionary biology, phylogenetic trees represent the evolutionary relationships between species. In the construction of phylogenetic trees, the leaves of the trees represent current species whose genomes are annotated by permutations, and the internal nodes represent ancestral genomes whose genomes are annotated by PO-trees. In order to determine the evolutionary relationships between different species, it is necessary to quantify the distances between the known permutations and the permutations in the constructed PQ-trees. Based on the measurement of breakpoint distance, we investigatep-Minimum Breakpoint Median from the PQ-tree. Given a PQ-tree and the correspondingppermutations, the goal is to identify a permutation generated by the PQ-tree that holds the minimum breakpoint distances relative to theppermutations. Our study shows that whenp≥2, thep-Minimum Breakpoint Median problem from PQ-tree is NP-complete. Moreover, whenp=1, the problem is fixed parameters tractable. To solve the 1-Minimum Breakpoint Median from PQ-trees, we propose a Fixed-Parameter Tractable algorithm whose computation complexity isO(3Kn) whereKis the optimized breakpoint distance.

Key wordsPQ-tree; breakpoint distance; fixed-parameter tractable; permutation; NP-complete

摘要PQ-树是一种树状数据结构，用来表示元素排列集合.虽然消逝物种完整基因组序列具有不确定性，但是根据同源物种可以确定部分基因的相对位置，所以可以利用PQ-树来存储消逝物种的基因组.在生物学中，进化树用来表示物种之间的进化关系.当构建生物进化树时，叶子结点表示现存物种，其基因组用排列表示；内部结点为祖先物种，其基因组用PQ-树表示.为了确定物种间的进化关系，需要确定PQ-树可以产生的排列与已知排列之间的距离.以断点距离为标准，研究了p-PQ-树断点中心问题，即从给定PQ-树中产生一个排列，使之与给定的p个排列的断点距离之和最小.证明当p≥2时，p-PQ-树断点中心问题是NP-完全的.当p=1时，p-PQ-树断点中心问题是参数化可计算的，针对1-PQ-树断点中心问题，提出了时间复杂度为O(3Kn)的参数化算法，其中K为最优解的断点距离.

关键词PQ-树；断点距离；固定参数可解；排列；NP-完全

PQ-树是由Kellogg和George[1]发现并命名的一种树状数据结构，可以用来表示元素排列的集合.PQ-树主要用来解决一些目标是寻找满足各种约束的排列的问题，在这些问题中，通过一次添加一种约束的方式编辑PQ-树的结构，使得编辑后的PQ-树能表示满足约束的排列.PQ-树的主要应用有：验证矩阵是否具有连续1性质[1]、判定图的平面性[2]等.PQ-树是字符表Σ={1,2,…,n}上的一棵平面有根树，它有3类结点：叶子结点、P结点和Q结点，每个叶子结点表示字符表中的一个元素，任意2个叶子结点表示的元素不同，非叶子结点被标记为P结点或Q结点.

由于利用现有技术构建祖先基因组时，只能推测出祖先基因组的连续遗传区，不能确定祖先基因组的全序列，如何构建消逝物种的全基因组，已有大量的工作致力于此[3].文献[3]基于多重断点图的概念，提出了算法MGRA，利用该算法重构祖先基因组.文献[4]提出了基于现代物种区间邻接关系预测祖先物种区间顺序的算法.

在本文中，利用PQ-树来存储祖先基因组[5].在生物学中，进化树用来表示物种之间的进化关系.生物分类学家和进化论者根据各类生物间的亲缘关系的远近，把各类生物安置在有分枝的树状图表上，简明地表示生物的进化历程和亲缘关系.当构建生物进化树时，叶子结点表示现存物种，其基因组用排列表示，内部结点为祖先物种，其基因组用PQ-树表示，祖先基因组跟现存物种基因组的组成元素相同[6].为了确定物种间的进化关系，需要确定PQ-树可以产生的排列与已知排列之间的距离.文献[7]证明了2棵PQ-树的最小断点距离问题是NP-完全的,本文将证明一棵PQ-树与已知排列的最小断点距离问题也是NP-完全的.

本文中，以断点距离为标准，研究了p排列PQ-树断点中心问题[8].p排列PQ-树断点中心问题描述如下：给定一棵PQ-树T和p个排列s1,s2,…,sp，要求从T生成排列s，使得s与给定的p个排列s1,s2,…,sp的断点距离之和最小.如果PQ-树T可以生成所有可能的排列，则p排列PQ-树断点中心问题跟传统的断点中心问题就是等价的.现在已知3个排列的断点中心问题是NP-完全的，从而，当p≥3时，p排列PQ-树断点中心问题是NP-完全的(这是因为可以构造一棵只有1个P结点的PQ-树，所有元素作为该树的叶子结点，这样的PQ-树可以产生元素的任意排列[9]).

本文主要工作如下：

1) 对于p排列PQ-树断点中心问题，证明当p≥2时，该问题是NP-完全的.

2) 针对1-PQ-树断点中心问题，提出时间复杂度为O(3Kn)的参数化算法.

1相关概念

1.1断点距离

定义1. 邻接.Σ表示包含n个字符的字符表，s是Σ上的所有元素构成的排列，s中相邻2个元素a和b构成一个邻接ab或ba.我们认为邻接ab与ba是等价的.

定义2. 公共邻接与断点.给定2个排列s1与s2，如果ab或ba在s1与s2中都出现，则称ab是公共邻接;如果ab在s1中出现，但是ab和ba在s2中都不出现，则称ab是s1的一个断点;如果ab在s2中出现，但是ab和ba在s1中都不出现，则称ab是s2的一个断点.

定义3. 端点与公共端点.排列2端的2个元素称为端点，如果元素a既是排列s1的端点，又是排列s2的端点，则称a是公共端点.

定义4. 断点距离.令a(s1,s2)表示排列s1与s2的公共邻接的数目，t(s1,s2)表示排列s1与s2的公共端点的数目，则排列s1与s2的断点距离定义为

(1)

在排列s1与s2的两端分别加上元素0和n+1，可以得到规整后的断点距离：

(2)

1.2PQ-树

PQ-树是字符表Σ={1,2,…,n}上的一棵平面有根树.PQ-树有3类结点：叶子结点、P结点、Q结点.字符表中的每个元素用一个叶子结点来表示，任意2个叶子结点表示的元素不同.非叶子结点被标记为P结点或Q结点，1个P结点至少有2个子结点，1个Q结点至少有3个子结点.P结点的子结点的顺序可以随意排列，Q结点的子结点的顺序只能是正序或者反序.PQ-树只有2种可行操作，PQ-树可以通过可行操作实现等价变换：

1) 随意重排P结点的子结点顺序.

2) 将Q结点的子结点顺序翻转.

当且仅当存在一系列可行操作能将一棵PQ-树转化为另一棵PQ-树，则称这2棵PQ-树是等价的.

按照前序关系得到的PQ-树的叶子结点的排列称为PQ-树的标签，与某棵PQ-树T等价的所有PQ-树的标签称为该PQ-树产生的排列的集合，记为P(T).

1.3问题定义

p排列PQ-树断点中心问题(p-minimum break-point median from PQ-trees,p-MBM-PQ).

实例：字符表Σ上的PQ-树T和p个排列s1,s2,…,sp，|Σ|=n，正整数K.

22-MBM-PQ是NP-完全的

本节通过将三正则平面无桥连通图上的哈密顿路径问题规约到2-MBM-PQ，证明2-MBM-PQ问题是NP-完全的.已知三正则平面无桥连通图上的哈密顿路径问题是NP-完全的[10].

在文献[6]中，证明了2棵PQ-树的断点距离问题是NP-完全的.由于一棵PQ-树可以产生排列可能有若干个，因此，本文中研究的问题比文献[6]中研究的问题要简单的多，但本文中证明这个问题仍然是NP-完全的.

各顶点的度均相同的无向简单图称为正则图.各顶点度均为K的正则图称为K正则图.对于图G中的边e，若删除边e使得图G的连通分支数增加，则边e是G的桥.

规约的中心思想如下：对应于一个给定的三正则平面无桥连通图C，构造2-MBM-PQ问题的PQ-树T及2个排列s1，s2，其中PQ-树T的叶子结点对应于图C的所有顶点，2个排列s1与s2对应于图C的所有边.因此图C中有哈密顿路径当且仅当可以从PQ-树T生成排列s，使得s与s1，s2的公共邻接数之和为n-1(其中每个邻接对应于图C中的一条边).

给定一个三正则平面无桥连通图C=(C(V),C(E))，首先构造2-MBM-PQ问题的PQ-树T：T有2层，根结点是P结点，它有2个子结点：一个是P结点，存储C(V)的所有顶点；一个是Q结点，存储填充元素(填充元素是为了间隔非邻接顶点而添加的不同于图C中顶点的元素).

然后，构造2个排列s1与s2，s1，s2包含C(V)中的所有顶点以及填充元素，对于图C中的每对顶点vivj，如果(vi,vj)∈C(E),那么vivj或vjvi是s1或s2中的一个邻接，但不是s1与s2的公共邻接，如果(vi,vj)∉C(E)，则用其他顶点或者填充元素将vi与vj间隔开，使其在s1与s2中不能构成邻接.

引理1[11]. 任何三正则平面无桥连通图都有完美匹配，其完美匹配可以在多项式时间内计算得到.

下面，将描述构造排列s1，s2的具体步骤，该构造过程可以在多项式时间内完成.

步骤1. 计算三正则平面无桥连通图C=(C(V),C(E))的完美匹配M，从图C中删除M中的边，得到图C′=(C(V),C(E)-M)，则C′是由不相交的环路构成.

步骤2. 从任意顶点vi(vi∈C′(V))开始，遍历C′中vi所在环路上的所有顶点，得到一条路径P=vi,…,vj，对于顶点vk(其中(vj,vk)∈M)，如果vk已被某条路径遍历过，则重新选择一个顶点作为开始顶点，继续遍历C′中的环路；否则，如果vk还没被任何路径遍历过，那么将路径P通过边(vj,vk)扩展到其他环路.循环迭代这个过程直到所有的环路都被遍历.最后，利用M中的边连接得到的这些路径，直到没有两条路径可以被连接，从而构成最长的没有环路的路径，并把最终得到的路径集合放入s1中,将得到的路径集合记为P′.

步骤3. 将C中剩余的没被遍历的所有路径(不包含在路径集合P′中)放入s2.

引理2.C(V)中的每个顶点在s1中恰好出现1次.

证明. 由于图C是一个三正则平面无桥连通图，M是图C的完美匹配，那么C′=(C(V),C(E)-M)是由不相交的环路构成.步骤2中，遍历图C′中所有环路得到的路径集合放入s1中，其中，每个环路遍历且只遍历1次，所以，C(V)中所有顶点在s1中恰好出现1次.

证毕.

从图C中删除路径集合P′中的边，得到图C″.

引理3. 图C″中没有环.

证明. 对于图C″，可以证明结论：图C″中每个度为2的顶点都有1个度为1的邻居顶点，若该结论成立，则图C″中没有环.

注意到C″中每个度为2的顶点必定是P′中某条路径的端点.假设：1个度为2的顶点vr连接到2个度为2的顶点vs，vt，则vs，vt中至少有1个顶点跟vr不在同一条路径上，而根据上述构造排列s1与s2的过程，这样的2条路径在步骤2中应该被连接起来，这与每个度为2的顶点必定是P′中某条路径的端点相矛盾，所以图C″中每个度为2的顶点都有1个度为1的邻居顶点，所以图C″中没有环.

证毕.

引理4.C(V)中的每个顶点在s2中恰好出现1次.

证明. 由于C(V)中的每个顶点在s1中恰好出现1次(引理2)，所以C″中的顶点度数为1或2.又由于C″中没有环(引理3)，所以放入s2中的都是不相交的路径，所以C(V)中的每个顶点在s2中恰好出现1次.

证毕.

引理5. 如果边(vi,vj)∈C(E)，则在s1或s2中，存在邻接vivj或vjvi，但vivj或vjvi不是s1与s2的公共邻接.

证明. 根据s1，s2的构造过程，对于图C中的每条边(vi,vj)，存在且只存在2种情况中的1种：

1) (vi,vj)或(vj,vi)在步骤2中被放入s1中，则在s1中存在邻接vivj或vjvi.

2) (vi,vj)或(vj,vi)在步骤3中被放入s2中，则在s2中存在邻接vivj或vjvi.

(vi,vj)或(vj,vi)或者在步骤2中被放入s1中，或者在步骤3中被放入s2中，但不会同时放入s1与s2中，所以邻接vivj或vjvi只能在s1或s2中存在，但不是s1与s2的公共邻接，所以该引理成立.

证毕.

引理6. 如果边(vi,vj)∉C(E)，则在s1和s2中，不存在邻接vivj或vjvi.

证明. 根据s1，s2的构造过程，放入s1，s2中的只能是图C中的边，所以如果(vi,vj)∉C(E)，则在s1，s2中不存在邻接vivj或vjvi，所以该引理成立.

证毕.

下面，我们完成三正则平面无桥连通图上的哈密顿路径问题到2-MBM-PQ问题的规约，证明2-MBM-PQ问题是NP-完全的：

1) 利用不同的填充元素将s1以及s2中的路径分别间隔开.

2) 构建4个子排列x1x2x3x4，x2x4x1x3，x5x6x7x8，x6x8x5x7，分别把x1x2x3x4与x5x6x7x8放在排列s1与s2的两端；把x2x4x1x3放在PQ-树T的子Q结点的最左边，把x6x8x5x7放在PQ-树T的子Q结点的最右边.

3) 把s2中的所有填充元素放在s1中的x1的左边，把s1中的所有填充元素放在s2中x8的右边；把所有既在s1中又在s2中的填充元素放在PQ-树T的子Q结点的x2x4x1x3与x6x8x5x7之间，并且保证在s1或s2中邻接的两个填充元素在Q结点中不能相邻.

引理7. 三正则平面无桥连通图C存在一条哈密顿路径,当且仅当PQ-树T可以生成排列s，使得s与s1的公共邻接数加上s与s2的公共邻接数之和为n-1.

证明. 显然，没有公共邻接涉及填充元素.

充分性.如果三正则平面无桥连通图C有一条哈密顿路径，PQ-树可以产生一个排列s，排列s中的元素顺序与哈密顿路径中顶点的顺序一致，那么排列s中每一个邻接对应图C的哈密顿路径中的一条边.由于图C中的每条边被放入且只放入排列s1或s2中的1个，所以排列s与s1，s2的公共邻接数之和为n-1.

必要性.如果T可以生成排列s使得s与s1的公共邻接数加上s与s2的公共邻接数之和为n-1，由于T最多可以生成n-1个公共邻接，每个邻接对应于C中的一条边，所以，所有的这些边构成一条哈密顿路径.

证毕.

现在举例说明这个规约.给定一个三正则平面无桥连通图C，如图1(a)所示，图C的完美匹配如图1(b)所示：

Fig. 1　A cubic plannar bridgeless graph and its perfect matching.图1　三正则平面无桥连通图及其完美匹配

根据排列s1，s2的构造过程：从顶点v1开始，遍历环路v1v2v3v4v1上所有顶点，得到路径P=v1v2v3v4，对于顶点u4，由于(v4,u4)∈M且u4还没被遍历过，将路径P通过边(v4,u4)扩展到环路u4u1u2u3u4，得到P′=v1v2v3v4u4u1u2u3，将路径P′放入s1，将剩余的没被遍历的路径集合{v4v1v3,v2u2,u4u3u1}放入s2，添加填充元素#、$将s2中的路径间隔开，在s1，s2中添加子排列x1x2x3x4，x5x6x7x8，在s1中添加填充元素#，$，最终得到：

s1=#$x1x2x3x4v1v2v3v4u4u1u2u3x5x6x7x8,

s2=x1x2x3x4v4v1v3#v2u2$u4u3u1x5x6x7x8.

字符#，$是填充元素.PQ-树T的根结点是P结点，根结点有2个子结点，1个是P结点，1个是Q结点.P结点的叶子结点为：{v1,v2,v3,v4,u1,u2,u3,u4}，Q结点的叶子结点为：x2,x4,x1,#,x3,$,x6,x8,x5,x7.

重排P结点的叶子结点可以得到一个序列：[v1,v2,v3,v4,u4,u1,u2,u3].该序列对应C中的一条哈密顿路径，在得到的序列基础上添加填充元素#，$，可以得到一个排列s，使得s与s1，s2的公共邻接数之和为7.

引理8. 2-MBM-PQ问题是NP-完全的.

证明. 显然，2-MBM-PQ是NP的.根据引理5，可以看到本文的规约可以在多项式时间内完成，所以2-MBM-PQ是NP-完全的.

证毕.

由于p≥3时，p排列PQ-树断点中心问题是NP-完全的，综合引理6，可以得出如下结论：

推论1. 当p≥2时，p-MBM-PQ问题是NP-完全的.

31-MBM-PQ问题的参数化算法

本节提出一个参数化算法解决1-MBM-PQ问题，该算法的参数是问题最优解的断点距离.

判定问题Π、参数p、存在算法可以在O(f(p)nc)时间内解决该问题，其中f是只与p有关的函数，n是问题输入规模，c是与p无关的常数[12].这样的问题称为参数化问题，可以在O(f(p)nc)时间内解决该问题的算法称为参数化算法.

3.1PQ-树的图表示

首先介绍怎样图形化表示PQ-树.给定1-MBM-PQ问题的PQ-树T与排列s1，PQ-树T的每个结点对应图G的一个顶点.对应于叶子结点的顶点称为元素，对应于P结点的顶点称为超P顶点，对应于Q结点的顶点称为超Q顶点.2个顶点之间存在边，当且仅当它们是某个Q结点的相邻子结点.图G的边称为黑边.

根据T的层次关系，在图G中增加顶点嵌入信息.如果PQ-树中一个结点X是另一个结点Y的子结点，则在图G中，X对应的顶点嵌入到Y对应的顶点中，如图2所示.因此，当且仅当X是Z的子孙结点时，X对应的顶点嵌入到Z对应的顶点中.

将排列s1的信息增加到图G中.对于s1中每个邻接xy，如果图G中不存在黑边(x,y)，则在图G中增加一条蓝边(x,y)，令得到的新的图为G′，如图3所示.图G′中超顶点X的度定义为：连接X内顶点与X外顶点的蓝边的数目.

可以看到1-MBM-PQ问题跟最小路径覆盖问题关系密切.最小路径覆盖问题描述如下：给定一个图，寻找数目最少的路径，使之覆盖图的所有顶点，并且任何一个顶点有且只有一条路径与之关联[14].

Fig. 2　A PQ-tree and its graphical representation.图2　PQ-树及其图表示

3.21-MBM-PQ问题的参数化算法

通过下面的引理来描述如何求解问题的最优解.

引理9. 通过对图G′完成以下操作，可以得到1-MBM-PQ问题的最优解：

1) 如果元素x是Q结点Y的中间的子结点(其中Y的所有子结点都是叶子结点)，则删除所有与x关联的蓝边.

2) 如果元素x的度数超过2，则至多保留2条与x关联的蓝边，其余蓝边都删除.

3) 如果超顶点X的度数超过2，则至多保留2条与X内元素相关联的蓝边，其余蓝边都删除.

证明. 这里只讨论第3种情况.如果X度数超过2，为了将X嵌入某条路径，则必须删除与X相关联的多余边.如果连接到X内元素的蓝边超过2条，则不可能将X嵌入某条路径.

证毕.

在执行了引理9的步骤1操作之后，令r表示图G′中超顶点的最大度数，如果r≤2，则问题是平凡的，所以假定r≥3.该FPT算法利用有限搜索树的原理，处理度数超过2的超顶点.令K表示1-MBM-PQ问题的最优解的断点距离，f(K)表示搜索树的叶子结点数目，可以得到如下递推关系：

(3)

主要递推关系式可以化简为

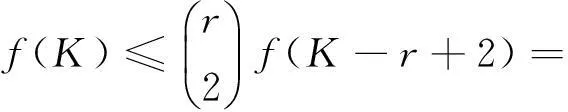
(4)

利用生成函数求解递推关系的方法，对式(4)进一步化简得到：

(5)

可以看到，当r=3时，取得最大值，则：

(6)

因此f(K)≤3K.

算法描述如下：

算法1.One-MBP-PQ(T，s1).

输入：PQ-树T、排列s1、整数K；

输出：由T生成的排列s，s与s1之间的断点距离不超过K.

步骤1. 根据T，计算得到图G；

步骤2. 根据T的层次关系，在图G中增加嵌入信息；

步骤3. 对应于s1中的所有邻接，在图G中添加蓝边，得到图G′；

步骤4. 令U表示从G′中删除的蓝边的集合；

步骤5. while |U|≤K

步骤5.1. 如果元素x是Q结点Y的中间的子结点(其中Y的所有子结点都是叶子结点)，则删除所有与x关联的蓝边，并把删除的蓝边放入U；

步骤5.2. 如果元素x的度数超过2，保留2条与x关联的蓝边，删除其余蓝边，并把删除的蓝边放入U；

步骤5.3. 如果超顶点X的度数超过2，保留2条与X内元素关联的蓝边，删除其余蓝边，并把删除的蓝边放入U；

步骤6. 如果最终得到的图由路径组成，则返回排列s，否则，返回“无解”.

当从图G′中删除K条蓝边后，要做的就剩下验证所得的图是否由路径组成，如果在删除K条蓝边后，所有顶点度数都不超过2，那么验证所得的图是否由路径组成，就可以转化为验证图中是否有环路存在.在删除K条蓝边后，如果没有找到可行解，则返回“无解”.这可以在O(n)的时间内完成.因此，一旦计算得到G′，可以利用有限搜索树[15]原理实现一个时间复杂度为O(3kn)的算法.

在图3中，针对上述算法举一个简单的例子.图3(a)中，给定PQ-树T，给定排列s1=“0123456789”，图3(b)中，图G′是计算所得(图中虚线边代表算法中添加的蓝边).该实例最优解的断点距离K=1.根据上述算法，需要在图G′中删除一条蓝边，例如，对于超顶点“105”，其度数为3，所以至少删除(2,1)(5,6)(4,5)的一条边，为了使最终得到的图由路径组成，删除蓝边(4,5)，此时可以得到最优解排列s=“4321056789”，且s与s1之间恰好有一个断点.

Fig. 3　An example for the FPT algorithm.图3　参数化算法示例

根据上述算法，可以得到结论：1-MBM-PQ问题存在时间复杂度为O(3kn)的算法，其中n是元素个数，K是最优解的断点距离.

4结束语

本文主要分析讨论了p-PQ-树断点中心问题，在介绍了PQ-树、断点距离等相关概念后，证明了当p≥2时，p-PQ-树断点中心问题是NP-完全的，然后针对1-PQ-树断点中心问题，提出了时间复杂度为O(3kn)的参数化算法.

目前，1-MBM-PQ问题的复杂性还是未知，设计PQ-树断点距离问题的有效算法也值得继续研究.

参考文献

[1]Booth K S, Lueker G S. Testing for the consecutive ones property, interval graphs, and graph planarity using PQ-tree algorithms[J]. Journal of Computer and System Sciences, 1976, 13(3): 335-379

[2]Ou Liancheng. Testing for graph planarity using PQ-tree algorithms[J]. Computer Engineering and Science, 1990, 12(2): 44-50 (in Chinese)(欧连成. 用 PQ-树算法判定图的平面性[J]. 计算机工程与科学, 1990, 12(2): 44-50)

[3]Alekseyev M A, Pevzner P A. Breakpoint graphs and ancestral genome reconstructions[J]. Genome Research, 2009, 19(5): 943-957

[4]Ma J, Zhang L, Suh B B, et al. Reconstructing contiguous regions of an ancestral genome[J]. Genome Research, 2006, 16(12): 1557-1565

[5]Rascol V L, Pontarotti P, Levasseur A. Ancestral animal genomes reconstruction[J]. Current Opinion in Immunology, 2007, 19(5): 542-546

[6]Chauve C, Tannier E. A methodological framework for the reconstruction of contiguous regions of ancestral genomes and its application to mammalian genomes[J]. PLoS Computational Biology, 2008, 4(11): e1000234

[7]Jiang H, Chauve C, Zhu B. Breakpoint distance and PQ-trees[C]Proc of the 21st Annual Symp on Combinatorial Pattern Matching. Berlin: Springer, 2010: 112-124

[8]Watterson G A, Ewens W J, Hall T E, et al. The chromosome inversion problem[J]. Journal of Theoretical Biology, 1982, 99(1): 1-7

[9]Sankoff D, Blanchette M. Multiple genome rearrangement and breakpoint phylogeny[J]. Journal of Computational Biology, 1998, 5(3): 555-570

中图法分类号TP301.6

通信作者：姜海涛(htjiang@sdu.edu.cn)

基金项目：国家自然科学基金项目(61202014，61472222)；山东省自然科学基金项目(ZR2012FQ008)；中国博士后科学基金项目(2011M5001133，2012T50614)

收稿日期：2014-11-17；修回日期：2015-01-27

This work was supported by the National Natural Science Foundation of China (61202014，61472222), the Natural Science Foundation of Shandong Province of China (ZR2012FQ008), and the China Postdoctoral Science Foundation (2011M5001133，2012T50614).