基于迁移共享空间的分类新算法

董爱美　毕安琪　王士同

1(江南大学数字媒体学院　江苏无锡　214122)

2　　　(齐鲁工业大学信息学院　济南　250353)

(amdong@163.com)



基于迁移共享空间的分类新算法

董爱美1,2毕安琪1王士同1

1(江南大学数字媒体学院江苏无锡214122)

2(齐鲁工业大学信息学院济南250353)

(amdong@163.com)

A Classification Method Using Transferring Shared Subspace

Dong Aimei1,2, Bi Anqi1, and Wang Shitong1

1(SchoolofDigitalMedia,JiangnanUniversity,Wuxi,Jiangsu214122)

2(SchoolofInformation,QiluUniversityofTechnology,Jinan250353)

AbstractTransfer learning algorithms have been proved efficiently in pattern classification filed. The characteristic of transfer learning is to better use one domain information to improve the classification performance in different but related domains. In order to effectively solve the classification problems with a few labeled and abundant unlabeled data coming from different but related domains, a new algorithm named transferring shared subspace support vector machine (TS3VM) is proposed in this paper. Firstly a shared subspace used as the common knowledge between source domain and target domain is built and then classical support vector machine method is introduced to the subspace for the labeled data, therefore the resulting classification model has the ability of transfer learning. Specifically, using the theory of transfer learning and the principal of large margin classifier, the proposed algorithm constructs a shared subspace between two domains by maximizing the joint probability distribution of the labeled and unlabeled data. Meanwhile, in order to fully consider the distribution of the few labeled data, the classification model is trained in the augmented feature space consisting of the original space and the shared subspace. Experimental results confirm the efficiency of the proposed method.

Key wordsshared subspace; transfer learning; support vector machine; joint probability distribution; large margin classifier

摘要为解决来自不同但相关领域的大量无标签数据和少量带标签数据的分类问题,首先构造一个联系源域到目标域的共享特征空间,并将该空间引入经典的支持向量机算法使其获得迁移能力,最终得到一种新的基于支持向量机的迁移共享空间的分类新算法,即迁移共享空间支持向量机.具体地,该方法以迁移学习理论为基础,结合分类器最大间隔原理,通过最大化无标签数据和带标签数据的联合概率分布来构建无标签数据和带标签数据的共享空间;为充分考虑少量带标签数据之数据分布,在其原始特征空间和共享空间组成的扩展空间中训练分类模型.相关实验结果验证了该迁移学习分类器的有效性.

关键词共享空间；迁移学习；支持向量机；联合概率分布；大间隔分类器

随着信息技术的快速发展和互联网的日益普及,人们获得的信息呈现出越来越复杂的变化,例如绝大部分信息不带有标签,而少部分信息带有标签;并且大量的无标签信息和少量的带标签信息又来自不同但又有一定关系的问题领域.而传统半监督学习方法研究对象的特点是大量无标签数据和少量带标签数据来自相同的问题领域并且数据分布相同,那么如何充分利用这些来自不同但相关问题领域的大量无标签数据和少量带标签数据来训练模式分类模型是机器学习重点研究的问题之一.

为了解决上述问题,迁移学习得以提出,其旨在解决2个不同但相关领域的机器学习问题,且放松了训练数据和测试数据独立同分布之要求[1].迁移学习的关键是尽最大可能缩小源域和目标域数据间的差异,来寻找源域和目标域数据之间的“共同点”作为2者间的“桥梁”,从而实现从源域到目标域的知识迁移.近年来,不同的学者主要从2个角度来寻找源域和目标域间的“共同知识”[2-11]：数据样本和数据特征.前者通过样本加权方法从源域寻找与目标域样本相似度最大的样本来作为迁移的知识,后者通过各种不同方式学习源域和目标域的共享特征表示来作为迁移的知识.学习源域和目标域的共享特征表示的方法主要有: Pan等人[2]在2008年通过降维方式学习得到领域间共享的特征表示从而实现迁移分类:首先通过最大均值差异嵌入(maximum mean discrepancy embedding, MMDE)进行降维得到一个低维的映射空间,并在此空间中使得源域数据和目标域数据的均值中心对齐,以减小2个领域的差异,经过这种处理后的数据可以直接利用传统分类器对数据进行训练和泛化; Xie等人[3]在2009年同样也是通过降维的方法研究了特征缺失下的迁移问题,先通过填补缺失值将领域间的条件分布变得一致,然后利用降维的方法将领域间的边缘分布变得一致,最后利用一些传统分类器实现了利用源域判别信息对目标域数据的分类;Quanz等人[4]在2009年以正则风险最小化思想为基础,结合最大均值差(maximum mean discrepancy, MMD)方法,提出一种基于特征空间的大间隔直推式迁移学习方法(large margin projected transductive support vector machine, LMPROJ),该方法是以经验风险正则化分类为框架,通过寻求一个特征变换来缩小源域和目标域之间的差异达到迁移分类之目的;Pan等人[5]在2010年提出将不同问题领域中的特征分为领域相关特征和领域独立特征,通过领域相关特征建立领域间联系实现领域间的迁移,再基于谱图划分对数据进行分类;Pan等人[6]在2011年进一步基于降维的思想,提出了快速特征提取算法TCA来学习一个低维的映射空间,对MMDE算法在计算复杂度方面进行了可观的改善;Zhuang等人[8]在2012年针对跨领域文本分类问题特有的共性和个性特征提出了CD-PLSA迁移学习算法,并且应用到多源域和多目标域问题中;Shao等人[9]在2012年使用低秩表示学习低维共享子空间技术,并提出了低秩迁移子空间学习算法; Gupta等人[10]在2013年采用非负矩阵分解思想提出了正则化的共享空间迁移学习框架,在一定程度上提高了模型的学习性能.

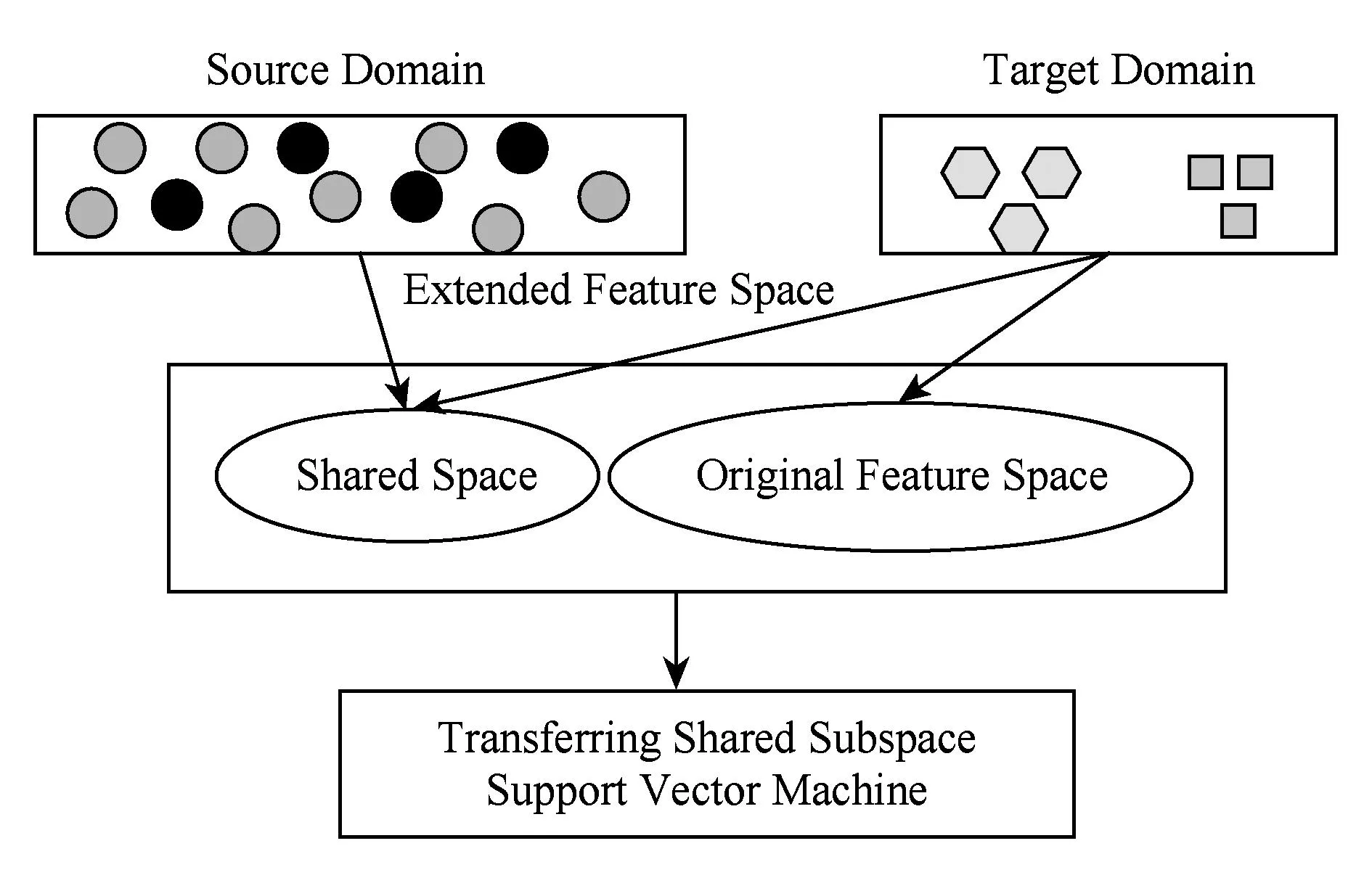
Fig. 1　The principal of TS3VM.图1　TS3VM原理图

纵观基于寻找源域和目标域的共享特征表示的迁移学习分类方法,尽管其取得了一定效果,但也存在不足之处:1)共享特征表示是在少量带标签数据原始空间基础上得到的,那么如果这些少量带标签数据受到噪声干扰,则会直接影响其分布情况,从而导致学习到的共享特征表示有误,最终使得迁移学习分类模型的性能降低;2)现有的基于共享特征表示的迁移学习分类方法仅仅考虑了领域间的共同特征表示,没有考虑目标域数据的分布情况,由于源域不带标签数据数量极大从而对共享特征表示的学习起着决定性的作用,这就导致仅仅在共享特征空间学习到的分类模型对于目标域数据来说是不完善的.结合这2方面的考虑,本文提出了迁移共享空间支持向量机算法:以分类器最大间隔原理为指导思想,通过最大化源域大量无标签数据和目标域少量带标签数据的联合概率分布来构建源域和目标域间的共享特征空间;为充分考虑少量带标签数据的分布情况及带标签数据类标可能受到攻击情况,在其原始特征空间和共享特征空间组成的扩展特征空间中训练分类模型.因为分类模型的训练既不仅仅是在原始特征空间也不仅仅是在共享特征空间中,从而既避免了原始类标受到噪声干扰又充分考虑了少量带标签数据的数据分布.迁移共享特征空间支持向量机算法(transferring shared subspace support vector machine, TS3VM)原理如图1所示.

1迁移共享空间支持向量机算法TS3VM

1.1问题描述

1.2TS3VM算法原理和目标函数

对于源域和目标域数据,根据Parzen窗法分别得到其概率分布的核密度估计函数如下:

(1)

(2)

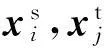
(3)

(4)

假设源域和目标域数据相互独立,那么在通过正交变换参数Θ投影后在r维的特征空间中亦最大可能满足联合分布独立性假设,所以由式(3)(4)得到在r维的特征空间中源域和目标域数据的联合概率分布为

(5)

令:

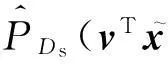
(6)

(7)

因为

所以有:

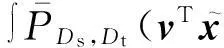
(8)

对于式(8)直接求解比较困难,利用泰勒展开定理进行近似变形得到:

(9)

结合式(8)(9)得到目标函数:

(10)

假设目标域数据在扩展后的总特征空间中分类超平面形式为

(11)

根据支持向量机最大间隔分类原则,同时要求源域和目标域数据在扩展的r维空间中联合概率分布最大,且对目标域数据在扩展后的特征空间中施加分类误差约束,得到TS3VM目标函数:

(12)

针对式(12),作如下说明:

1) 式(12)中第1项和第2项是结构风险项;第3项是经验风险项;第4项表示源域和目标域数据在扩展的r维的特征空间中的联合概率分布;通过对这4项的平衡期望达到最小的结构化风险.

2) 由式(12)可以看出,目标域数据的类标签仅仅用来维数扩展,从而避免了误标对最终分类模型的影响,使得最终分类模型有较强的抗噪性.

3) 由式(12)可以看出,在扩展后的特征空间中对目标域数据施加分类误差约束,既充分利用源域和目标域间的共性“知识”来获得正迁移效果,又充分考虑了目标域数据的数据分布,使得最终分类模型在目标域数据上性能最优,这也是本文采用扩维思想而不是采用传统降维思想来进行迁移分类的动机之一.

4) 从目标函数的构造过程可以看出,TS3VM方法在目标域数据数量远远小于源域数据数量且目标域数据类标受到攻击而产生误标情况下,具有很好的鲁棒性.

1.3TS3VM算法目标函数参数学习规则

(13)

其中有3个变量h,v,Θ需要同时优化.直接对这些参数优化是比较困难的.本文采用模糊聚类、模糊神经网络等技术中经常采用的交替迭代策略[12-15]对式(13)进行参数优化.在该迭代过程中包含3个主要步骤:

1) 固定({Θ,v}),优化式(13)学习得到{h};

2) 固定({Θ,h}),优化式(13)学习得到{v};

3) 固定({v,h}),优化式(13)学习得到{Θ}.

下面通过3个定理给出目标函数中的3个变量的学习规则：

定理1. 假设变量v,Θ固定,则式(13)中变量h的最优值可以通过对一个线性方程组求解得到.

证明. 假设变量v,Θ固定,当优化变量h时,式(13)可写为

(14)

构造目标函数J5的拉格朗日函数:

(15)

其中，αj为拉格朗日乘子且αj>0，j=1,2,…,nt,式(14)取得极值的必要条件为式(15)对h和ξj(j=1,2,…,nt)的偏导数为0,于是得到:

(16)

式(16)写成线性方程组的形式为

(17)

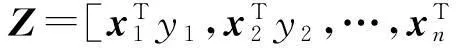
证毕.

定理2. 假设变量h,Θ固定,则式(13)中变量v是一个解析解,具体形式为

(18)

证明. 假设变量h,Θ固定,式(13)变为

(19)

目标函数J7取最小值的必要条件是其对v的偏导数为0r×1,即:

从而有:

此时v是一个解析解.

证毕.

定理3. 假设变量h,v固定,则式(13)中变量Θ的求解可以用梯度下降法求解得到,并且梯度下降法中的步长具有解析解的形式.

证明. 假设变量h,v固定,式(13)变为

(20)

假设隐变量的域记为Ω⊥,则Ω⊥={Θ⊂r×d}∩{Θ ΘT=Ir×r},因为Ω⊥中的约束条件Θ ΘT=Ir×r和正则化项具有相似的作用,所以可以把式(20)中的约束条件去掉而得到一个形式简单的优化问题.目标函数式J8对变量ΘT求偏导数为

(21)

则变量ΘT可以用梯度下降法求解得到,梯度下降规则为

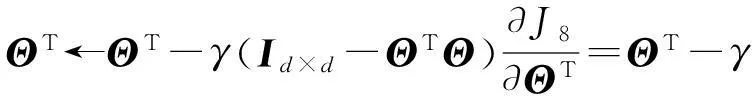
(22)

为得到变量ΘT的步长γ的解析解,把式(21)代入到式(22)中,得到:

(23)

从而有:

(24)

进一步,令:

(25)

则有:

(26)

(27)

把式(26)(27)代回式 (20)，得到关于γ的函数:

(28)

记:

t2=Mv,

则式(28)变为

(29)

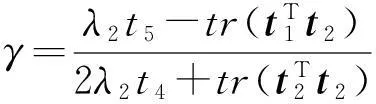
证毕.

1.4TS3VM算法描述

根据1.1～1.3节分析和推导,给出TS3VM算法描述.

算法1. TS3VM算法.

参数:源域和目标域数据特征扩展的维数r、参数C,λ1,λ2;

初始化:参数h0,Θ0,其中h0∈d,Θ0∈r×d,当前迭代值iter=0,设置最大迭代次数itermax和误差阈值ε1.

Repeat

Step1. 根据定理2计算viter;

Step2.iter=iter+1;

Step3. 根据定理3采用梯度下降法计算Θiter∈

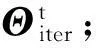
Step4. 根据定理1计算hiter;

1.5TS3VM算法收敛问题说明

对于TS3VM算法,以步骤iter+1的迭代学习为例对其收敛性作如下分析:

1) 在步骤iter+1,固定viter,Θiter不变,由定理1可知hiter+1是线性方程组的解,从而可以确保变量hiter+1在步骤iter+1取得全局最优解.

3) 在步骤iter+1,固定hiter,viter不变,对式(20)进行迭代优化,根据梯度下降算法的性质可知所得到的解Θiter是式(20)的某个局部最优解的近似解,即J8(Θiter+1)≤J8(Θiter).

据上述分析可知,TS3VM算法并不能保证严格的收敛.交替迭代优化技术在智能模型学习方法中[9-12]经常被使用,如经典的FCM等聚类算法,其通常能收敛于某个局部最优解或鞍点．虽然此类算法目前在理论上不能保证是严格收敛的或是有条件收敛的,但已有的采用交替迭代优化技术的迭代算法表明此优化技术在大多数场合是非常简单而有效的[9-12].

正如文献[12]指出的: 此类交替迭代的优化方法其收敛性仍是一个有待进一步深入探讨的开放性问题,保证该类方法的严格收敛是一个值得深入研究的课题.另外,由于初始化等不同因素的影响,目前许多交叉迭代算法多次执行后最终可能收敛于不同的局部最优解.针对此问题一个可行的解决方案是探讨新的优化算法来求解给定的优化目标函数.例如,近年来具有更好寻优能力的进化计算优化技术(遗传算法、粒子群算法等)已受到较多关注并被尝试应用于优化不同的建模模型.

对TS3VM算法的说明有2点:

1) 在变量初始化阶段,变量h,Θ随机初始化,因此在实验部分进行多次实验取平均值作为最终实验结果,尽量减少随机初始化带来的不确定性.

2) 对于迭代过程中的收敛条件,在算法设计中一方面通过阈值来控制,即当连续多次(比如10次)更新迭代相应的变量不再发生变化时,达到收敛;另一方面为保险起见,设置了最大迭代次数,对算法能够进行的最大迭代次数进行限制，几个收敛条件满足一个即停止迭代.

2实验分析

为验证TS3VM算法的有效性,在人造数据集(2-moons)和3个文本数据集上(20NewsGroup[16],Reuters-21578[13],Email Spam[17])进行了实验.采用比较算法有:SVM,TSVM[18],LMPROJ[4],TCA[6]. 采用SVM算法的目的是为了验证目标域中带标签数据数量非常少不足以训练一个高性能的分类器;算法TSVM是综合利用带标签数据和无标签数据的传统模式分类方法,采用其目的是为了验证在训练分类模型过程中引入迁移学习思想来综合利用带标签数据和无标签数据较传统模式分类方法优越;算法LMPROJ为迁移类算法，采用其目的是为了验证半监督的迁移学习方法和无监督的迁移学习方法的性能优劣;算法TCA为迁移类算法,采用其目的是为了验证在相同场景设置下,针对基于降维思想的迁移分类算法来说,本文所提的基于扩维的迁移分类算法表现出可比较的性能.对于SVM,由libsvm[19]软件实现,参数C取值范围为{0.1,0.2,0.5,1,2,5,10,20,50,100},采取5重交叉验证法来选取最优值.其他算法都在Matlab(R2009a)环境下实现且均通过网格搜索的方式来确定优化的模型参数.

具体来说,对于算法TSVM,参数C1和C2的取值范围为{10-5,10-4,10-3,10-2,10-1,1,10,102,103,104,105};对于算法LMPROJ,参数λ的取值范围为{210,211,212,213,214,215,216,217,218,219,220},参数λ2的取值范围为{2-5,2-4,2-3,2-2,2-1,1,2,22,23,24,25},参数C的取值范围为{2-6,2-5,2-4,2-3,2-2,2-1,1,2,22,23,24,25,26}; 对于算法TCA,参数μ的取值范围为{10-3,10-2,10-1,1,10,102,103}.对于TS3VM方法中的共享空间维数r需要人工确定,在当前主流的基于空间的分类方法中一般采用网格寻优或实验验证的方法确定,例如Ando[20]方法、Zheng[21]方法和Ji[22]方法.对于文本数据集,本文借鉴Ando方法的思想,只关心共享特征空间维数r在10～100之间的范围{5,10,15,20,25,30,35,40,45,50,55,60,65,70,75,80,85,90,95,100};对于人造数据集,扩展维数固定为1.参数C取值范围为{10-5,10-4,10-3,10-2,10-1,1,10,102,103,104,105}.参数λ1,λ2的取值范围为{2-6,2-5,2-4,2-3,2-2,2-1,1,2,22,23,24,25,26}. 所有参数r,C,λ1,λ2均通过网格搜索的方式确定最优值.详细参数敏感性实验参见2.3节

2.1数据集描述与设置

1) 2-moons数据集: 人工生成1个包含 600个样本的双月形2维样本集作为源域数据集,正负类样本各为300个;将源域数据按逆时针方向分别旋转30°,45°,60°,得到目标域数据集.另外,把目标域带标签数据的标签部分弄错,得到部分数据误标的目标域数据集,如图2所示.为了适应TS3VM算法之研究场景,对源域和目标域样本作如下处理:对于源域样本,去掉所有的标签信息;对于目标域样本,随机选择正负样本各30个作为训练样本.另外为了验证TS3VM算法对类标攻击的鲁棒性,把目标域中的部分训练样本类标弄错(误标样本比例设为20%).

2)文本数据集: 20NewsGroup数据集包含近20 000新闻组的英文文档,大约分成20类,包含6个顶层类别,每个顶层类别下分别包含若干个子类别. Reuter-21578包含近21 000个文档集,分为orgs,people,places三个大类,每个类别下面包含了相应的子类别.为了适应本文研究场景,对于20News-Group数据集:分别从顶层大类中抽取 4个大类以构建学习数据集;对于Reuter-21578数据集:数据基于子类进行分割,分别从顶层大类中抽取3个大类以构建学习数据集,其中每2个大类分别选作正类和负类不同的子类认为不同的领域.Email Spam数据集包含User1,User2,User3这3个子集代表3个不同用户.学习任务是划分出spam邮件和非spam邮件.由于数据集中不同用户的spam邮件和非spam邮件是不同的,因此3个email数据集的数据分布是不同但相关的.为适应本文研究场景设置,构造了3个迁移数据集.详细信息见表1和表2所示.

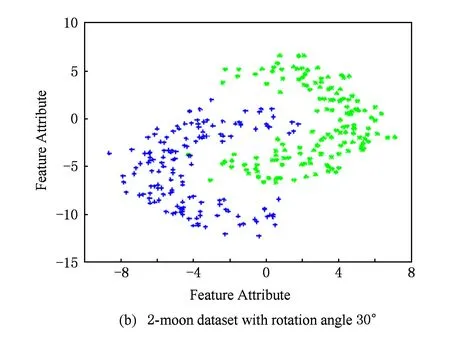
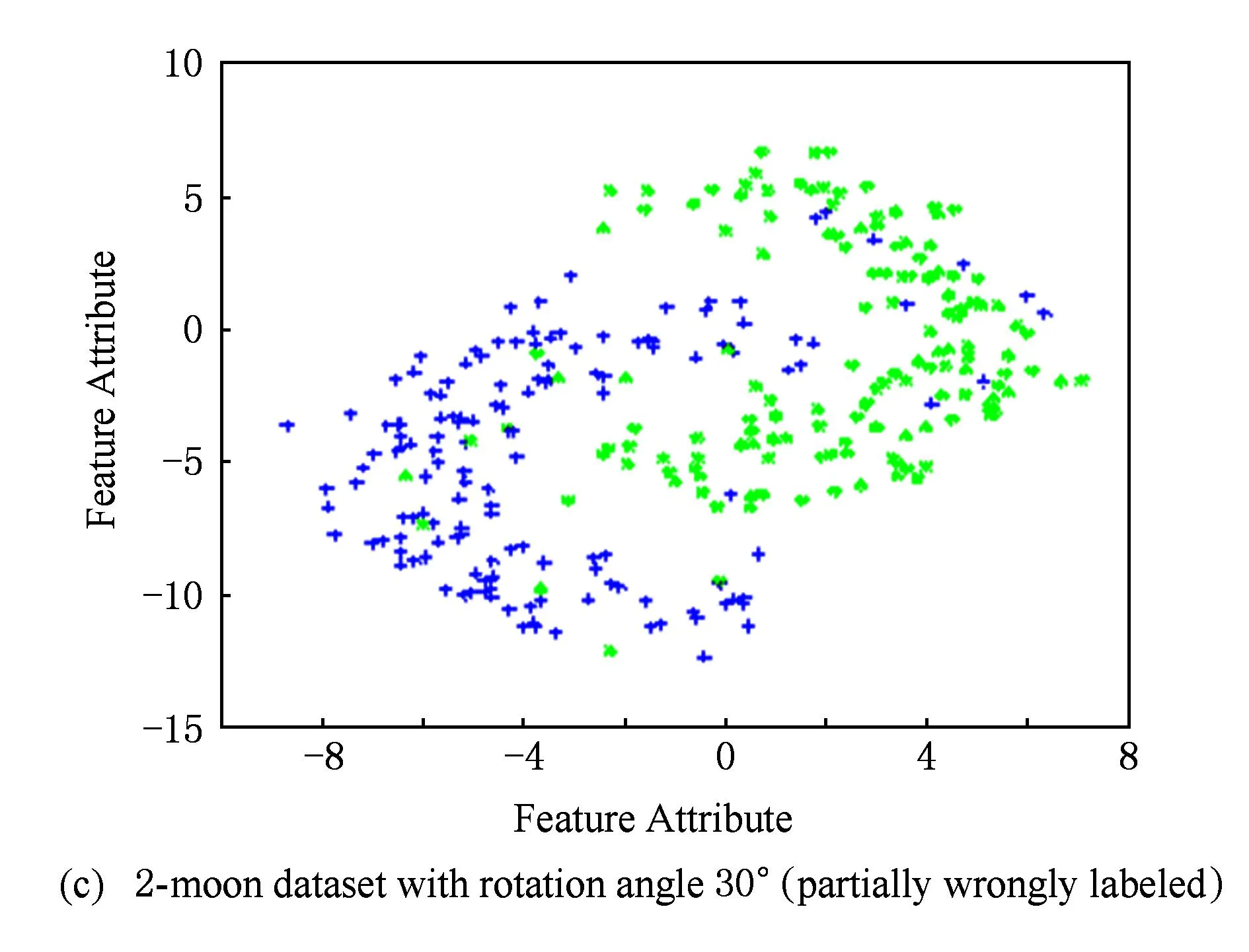
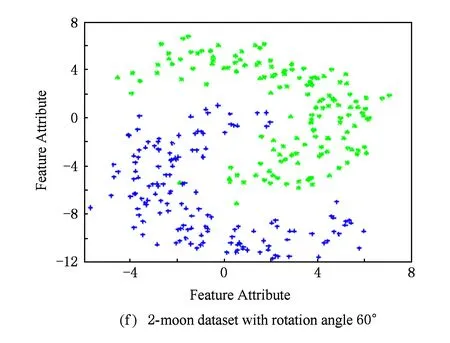
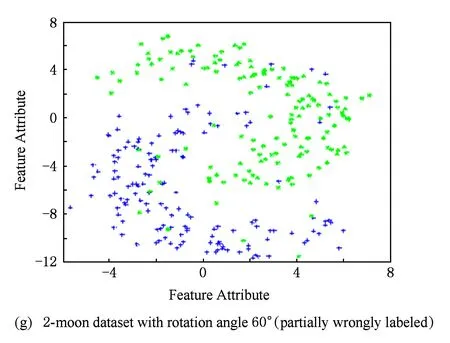
Fig. 2Four 2-moon datasets with different rotation degrees.
图2旋转不同角度的双月型数据集

Table 1　Transfer Learning Text Classification Datasets 20NewsGroup

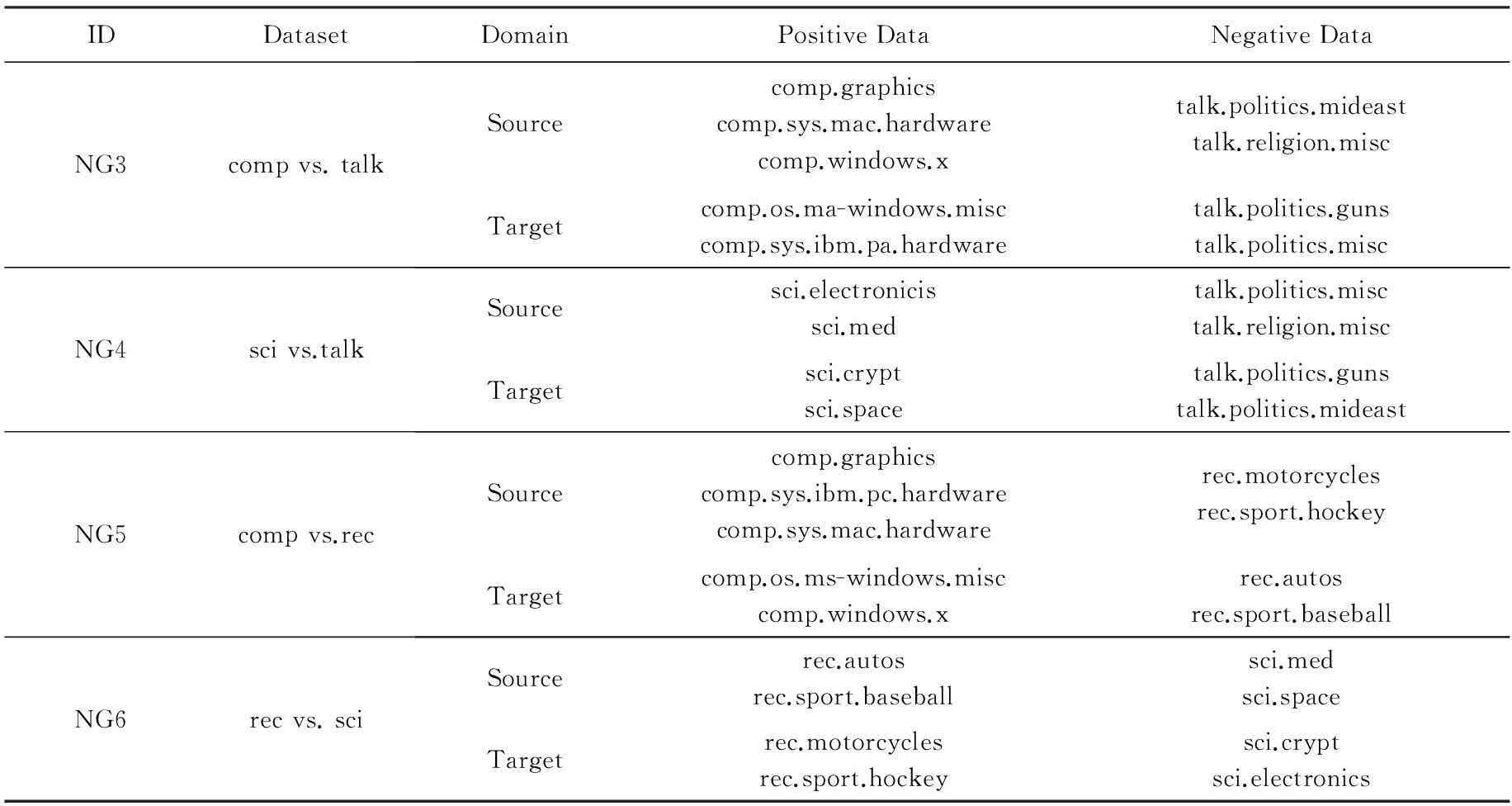
Continued (Table 1)

Table 2Transfer Learning Text Classification Datasets Reuter-21578 and Email Spam

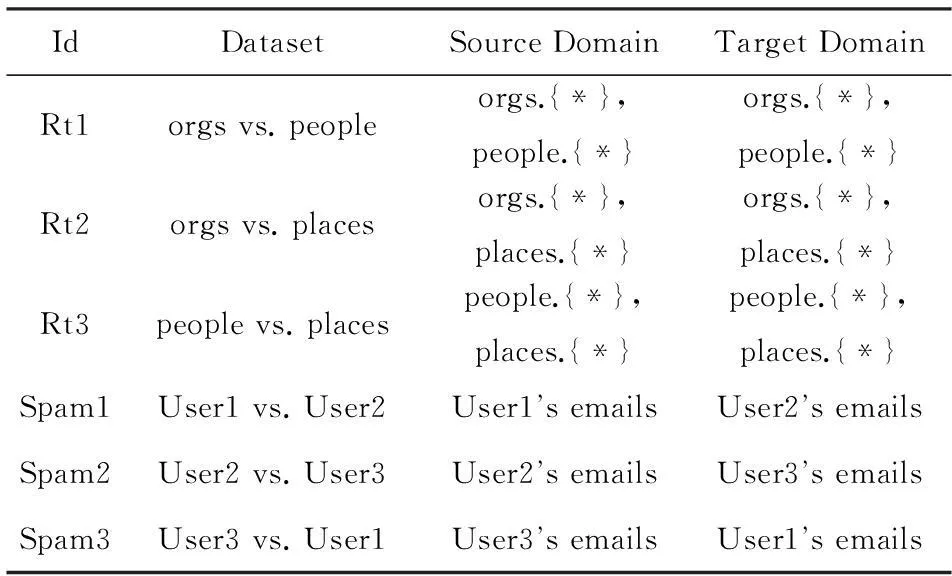
表2　迁移学习文本分类数据Reuter-21578和Email Spam

2.2实验结果与讨论

人造数据集的实验结果如表3所示,3个文本数据集的实验结果如表4～5所示.需要说明的是,本文对所有方法对参数均使用交叉验证法进行学习,并取最优结果进行记录.

由表3～5所示结果可以看出：

1) 基线方法 SVM 的训练集是目标域中少量的带标签数据,不足以训练一个高性能的分类器,故在所有数据集上的分类性能均低于其他学习方法;

2) 另外一个基线方法 TSVM虽然其训练集包括源域中大量不带标签数据,但是由于源域和目标域数据的数据分布不同,故在大部分数据集上分类性能低于其他迁移学习类方法,这也进一步说明了使用传统的半监督模式分类算法不能很好地解决数据分布不同之下的数据分类问题;

3) 迁移分类算法LMPROJ在大部分数据集上的分类性能高于传统半监督模式分类方法而低于其他2个迁移分类算法,因为LMPROJ算法中目标域数据不带有类标信息,属于无监督迁移分类;

4) 本文所提算法TS3VM在3个迁移分类算法中表现出鲁棒的分类性能,这进一步说明在迁移分类学习中采用扩维的思想较TCA算法采用降维的思想,对最终模式分类器来说效果更好,因为扩维的思想既考虑了源域和目标域领域间的共性知识又充分考虑了目标域数据的特有数据分布情况;

Table 3　Classification Accuracy Comparison on 2-moon with Different Rotation Angle

Table 4　Classification Accuracy Comparison on 20NewsGroup

Table 5　Classification Accuracy Comparison on Reuter-21578 and Email Spam

5) 尽管在部分数据集上(比如Spam2数据集)本文所提算法没有表现出最佳的均值精度,但是在方差中表现出了优势.

6) 更重要的是,从表3可以看出,在目标域数据类标受到攻击产生误标的情况下,本文所提算法表现出较强的鲁棒性,对最终分类器的影响甚微.这也进一步表现出本算法的相对于传统半监督分类算法和迁移分类算法的优点:在一定程度上摆脱了对已知类标数据类标的依赖性.

2.3参数敏感性实验

在评价某个参数的性能影响时,先固定其他3个参数的最优值.采用数据集NG1和Spam2作为实验数据,图3～6分别显示了上述4个参数对所提方法的性能影响.由此可得如下结论:

1) 由图3可以看出,所提方法是基于特征扩维的共享特征空间分类学习模型,因此对扩展的共享特征空间维数r具有较大程度的敏感性.即对于不同的数据集r的取值明显影响所提方法的最终性能,这也进一步说明了针对不同的数据集扩展的共享特征空间维数r协调的重要性,同时这也是本文作者下一步要深入研究的方向之一.

2) 由图4可以看出,在本文所考虑C的所有取值范围内,分类精度变化幅度较大.这进一步说明了，

Fig. 3　Influence of parameter r on accuracy.图3　参数r对分类精度的影响

Fig. 4　Influence of parameter C on accuracy.图4　参数C对分类精度的影响

Fig.5　Influence of parameter λ1 on accuracy.图5　参数λ1对分类精度的影响

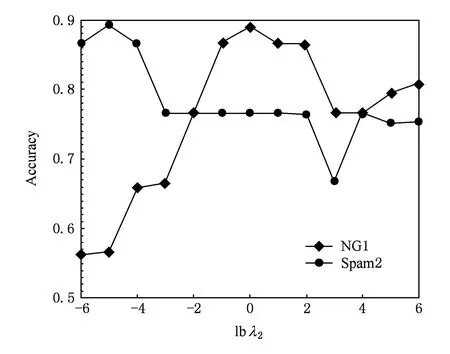
Fig. 6　Influence of parameter λ2 on accuracy.图6　参数λ2对分类精度的影响

基于结构风险最小化学习模型对参数C具有较大程度上的敏感性,即C在一定范围内的不同取值明显影响所提方法的泛化性能.

3) 由图5可以看出,由于本文所提方法基于最大间隔原则,故对平衡参数λ1具有较大程度的敏感性,即λ1在一定范围内的不同取值明显影响分类器最终性能.

3结论

综合利用相关领域的大量无标签数据来指导目标领域少量带标签数据来训练学习分类器是机器学习研究的热点之一.本文在半监督学习中引入迁移思想,根据分类超平面最大间隔和联合概率分布最大原则来充分挖掘无标签和带标签数据间的“共同”知识,在“共同”知识基础之上又结合少量带标签数据的数据分布,提出了基于迁移共享特征空间的模式分类算法.本文所提算法具有两大优点：1)从数据特征空间扩维的角度出发,既考虑带标签数据和无标签数据的“共同”知识,又考虑了少量带标签数据的数据分布;2)对目标域施加分类误差约束是在扩展后的特征空间而不是在原始特征空间,因此最终分类器在一定程度上摆脱了对带标签数据类标的依赖性.在大量相关数据集上的实验也验证了本文所提方法的有效性.

目前来看,本文所提方法的一个不尽人意之处是扩展的特征空间维数的确定还没有一个理论性的结论,而是采用传统的实验验证及网格寻优的方法确定,因此如何理论性地给出共享特征空间维数的确定方法是一项具有挑战性的研究话题,这是我们今后研究的重点之一.

参考文献

[1]Pan S J L, Yang Q. A survey on transfer learning[J]. IEEE Trans on Knowledge and Data Engineering, 2010, 22(10): 1345-1359

[2]Pan S J, Kwok J T, Yang Q. Transfer learning via dimensionality reduction[C]Proc of the 23rd Int Conf on Artificial Intelligence. Menlo Park, CA: AAAI, 2008: 677-682

[3]Xie S, Fan W, Peng J, et al. Latent space domain Transfer between High Dimensional overleaping distributions[C]Proc of the 18th Int Conf on World Wide Web. New York: ACM, 2009: 91-100

[4]Quanz B, Huan J. Large margin transductive transfer learning[C]Proc of the 18th ACM Conf on Information and Knowledge Management. New York: ACM, 2009: 1327-1336

[5]Pan S J, Ni X S J, et al. Cross-domain sentiment classification via spectral feature alignment[C]Proc of the 19th Int Conf on World Wide Web. New York: ACM, 2010: 751-760

[6]Pan S J, Tsang I W, Kwok J T, et al. Domain adaptation via transfer component analysis[J]. IEEE Trans on Neural Network, 2011, 22(2): 199-210

[7]Hong Jiaming, Yin Jian, Huang Yun, et al. TrSVM: A transfer learning algorithm using domain similarity[J]. Journal of Computer Research and Development, 2011, 48(10): 1823-1830 (in Chinese)(洪佳明, 印鉴, 黄云, 等. TrSVM: 一种基于领域相似性的迁移学习算法[J]. 计算机研究与发展, 2011, 48(10): 1823-1830)

[8]Zhuang Fuzhen, Luo Ping, Shen Zhiyong, et al. Mining distinction and commonality across multiple domains using generative model for text classification[J]. IEEE Trans on Knowledge and Data Engineering, 2012, 24(11): 2025-2039

[9]Shao M, Castillo C, Gu Z H, et al. Low-rank transfer subspace learning[C]Proc of the 12th Int Conf on Data Mining. Piscataway, NJ: IEEE, 2012: 1104-1109

[10]Gupta S K, Phung D, Adams B, et al. Regularized nonnegative shared subspace learning[J]. Data Mining and Knowledge Discovery, 2013, 26(1): 57-97

[11]Gu Xin, Wang Shitong. Fast cross-domain classification method for large multisourcessmall target domains[J]. Journal of Computer Research and Development, 2014, 51(3): 519-535 (in Chinese)(顾鑫, 王士同. 大样本多源域与小目标域的跨领域快速分类学习[J]. 计算机研究与发展, 2014, 51(3): 519-535)

[12]Deng Z H, Choi K S, Chung F L, et al. Enhanced soft subspace clustering integrating within-cluster and between-cluster information[J]. Pattern Recognition, 2010, 43(3): 767-781

[13]Yu J, Cheng Q S, Huang H K. Analysis of the weighting exponent in the FCM[J]. IEEE Trans on Systems, Man, and Cybernetics-Part B: Cybernetics, 2004, 34(1): 164-176

[14]Yang S, Yan S, Zhang C, et al. Bilinear analysis for kernel selection and nonlinear feature extraction[J]. IEEE Trans on Neural Networks, 2007, 18(5): 1442-1452

[15]Jiang Yizhang, Deng Zhaohong, Wang Shitong. Mamdani-larsen type transfer learning fuzzy system[J]. Acta Automatica Sinica, 2012, 38(9): 1393-1409 (in Chinese)(蒋亦樟, 邓赵红, 王士同. ML型迁移学习模糊系统[J]. 自动化学报, 2012, 38(9): 1393-1409)

[16]Gao J, Fan W, Jiang J, et al. Knowledge transfer via multiple model local structure mapping[C]Proc of the 14th

中图法分类号TP391.4

基金项目：国家自然科学基金项目(61202014，61472222)；山东省自然科学基金项目(ZR2012FQ008)；中国博士后科学基金项目(2011M5001133，2012T50614) 国家自然科学基金项目(61170122,61202311);山东省高等学校科技计划基金项目(J14LN05)

收稿日期：2014-11-17；修回日期：2015-01-27 2014-11-17；修回日期：2015-06-03

This work was supported by the National Natural Science Foundation of China (61202014，61472222), the Natural Science Foundation of Shandong Province of China (ZR2012FQ008), and the China Postdoctoral Science Foundation (2011M5001133，2012T50614).

This work was supported by the National Natural Science Foundation of China (61170122,61202311) and the Project of Shandong Province Higher Educational Science and Technology Program (J14LN05).