基于压缩的海量不完整数据近似查询方法

王　妍　刘赓浩　王俊陆　宋宝燕

1(辽宁大学信息学院　沈阳　110036)

2　　　(东北大学信息与工程学院　沈阳　110819)

(wang_yan@lnu.edu.cn)



基于压缩的海量不完整数据近似查询方法

王妍1,2刘赓浩1王俊陆1宋宝燕1

1(辽宁大学信息学院沈阳110036)

2(东北大学信息与工程学院沈阳110819)

(wang_yan@lnu.edu.cn)

A Compression-Based Approximate Query Method for Massive Incomplete Data

Wang Yan1,2, Liu Genghao1, Wang Junlu1, and Song Baoyan1

1(SchoolofInformation,LiaoningUniversity,Shenyang110036)

2(SchoolofInformationScienceandEngineering,NortheasternUniversity,Shenyang110819)

AbstractWith the explosive increase of data, incomplete data are widespread. Traditional methods of data repair will cause high processing cost for mass data, and cannot be fully restored. Thus the approximate querying on these huge amounts of incomplete data for meeting the given requirements attracted greater attention from academics. Therefore, this paper proposes an approximate query method for massive incomplete data based on compression. Tagging the missing attribute value field and finding out the frequent query conditions, this method compresses these data based on the statistical frequent query conditions, and establishes the corresponding indexes. According to the attribute partition rules, index files are compressed again in order to further save storage space. In the stage of query, this method uses encoding dictionary to make selection and projection operations on the index compression files for getting approximate query results of incomplete data in the end. Experimental results show that this method can quickly locate the position of incomplete data compression, improve the query efficiency, save the storage space, and ensure the integrity of the query results.

Key wordsincomplete data; approximate query; data compression; index; encoding dictionary

摘要随着数据的爆炸式增加，不完整数据普遍存在，传统的数据修复方法对于海量数据处理代价过高，且不能彻底修复，在这些不完整的海量数据上进行满足给定需求的近似查询引起了学术界的关注.因此，提出一种基于压缩的海量不完整数据近似查询方法，该方法对属性值缺失字段进行标记，根据频繁查询条件对标记后的数据进行压缩，并建立对应索引；根据属性划分对索引文件再次压缩以节省存储空间，采用编码字典对索引压缩文件进行选择和投影操作，最终获得不完整数据的近似查询结果.实验表明，该方法能够快速定位不完整数据的压缩位置，提高了查询效率，节省了存储空间，并且保证了查询结果的完整性.

关键词不完整数据；近似查询；数据压缩；索引；编码字典

随着信息技术的发展，数据规模不断增加，尤其是在以计算机和互联网为基础的应用中数据更是以指数形式增长.而在海量数据带来丰富信息的同时，也带来许多质量问题，这些问题严重地制约着数据的应用价值[1-2].其中，数据缺失是一个常见的现象.不合理地处理缺失数据将造成错误结果，甚至是严重的损失[3].因此，如何有效存储和管理有属性值缺失的海量数据,即海量不完整数据，是研究的重中之重.

近几年来，许多学者对海量不完整数据的处理进行了研究.现有的方法在对海量不完整数据进行操作之前，需要对其进行数据清洗[4-7]，然后再对清洗后的“干净”数据进行压缩存储[8-11]和管理.然而，对于海量数据而言，先进行数据清洗再操作数据有很多弊端.首先，基于数据的海量性，数据清洗的代价将会非常大；其次，清洗的结果会受到很多因素的影响，可能会引入新的“噪声”导致清洗结果并不准确；此外，数据清洗还会产生时效性问题，结果就是很多时效数据将失去意义.因此，我们的工作就是越过数据清洗直接对海量不完整数据进行压缩存储以及管理，而现有的压缩算法都是对完备数据的压缩，所以我们要设计一种新的适用于不完整数据的压缩算法，以及与其相对应的查询算法.由此可见，针对海量不完整数据的压缩与查询处理方法的研究是十分必要的[12].

针对上述问题，本文提出了一种基于压缩的海量不完整数据近似查询方法(compression-based approximate query for massive incomplete data, AQ-MI),该方法可以快速地定位查询数据的压缩位置，提高查询效率，还能够大幅度地减少存储空间，并且保证查询结果的完整性.本文的主要贡献有3点：

1) 提出一种面向海量不完整数据的压缩策略，利用频繁查询条件索引法，在被标记数据压缩时将每一元组所满足的不确定条件和确定性条件作为索引存储于索引表中.采用属性值缺失字段标记策略，对带有标记的字段进行重复压缩，以保证查询结果的完整性和可信性.还提出了一种基于Attr-1的索引文件压缩方法，进一步减少存储空间.

2) 提出一种无解压近似查询方法，查询时分析查询语句，对索引压缩文件进行相应的选择和投影操作，根据获得的被标记数据压缩地址，最终得到近似查询结果.

3) 设计了详细的性能评估实验，实验结果表明AQ-MI算法可以快速地定位查询数据的压缩位置，提高查询效率，还能够大幅度地减少存储空间，并且保证查询结果的完整性.

1相关工作

文献[4-7]是常见的对不完整数据的清洗方法.文献[4]采用基于记录删除的数据清洗策略，在查询之前先删除不完整的记录，再在“干净的”数据库上进行计算查询，虽然得到唯一确定的结果，但丢失了部分有价值的信息.文献[5-7]采用基于数据填充的数据清洗策略，在查询之前用一定值去填充属性值缺失的字段，从而使信息完备化，然而这种方法只是在一定程度上补以主观的估计值，不一定完全符合客观事实，而且对缺失值不正确的填充往往将新的噪声引入数据，使查询产生错误的结果.

对海量数据的压缩，最常见的方法是基于编码字典的压缩[8-10]，这类方法采用按列存储的思想对数据进行压缩，将对原始数据的查询转化为对压缩编码位的操作.文献[8-9]是对串表压缩算法LZW进行改进，主要思想是利用较短的码字表示较长的字符串来实现压缩.文献[10]应用一种对称编码SVC，进一步减短对应码字长度，提高测试数据的压缩效果.采用这种编码字典方法可以实现不解压直接查询，提高了效率，但是增加了匹配字典和维护字典的代价，不适用于更新频繁的系统.文献[11]提出一种海量数据压缩存储结构，在数据压缩时，为每条元组计算相应的索引项，该方法虽然在查询时可以提高效率，但对于海量数据而言，索引的规模也很大，即增加了大量额外的存储空间.

就目前的海量不完整数据的存储和管理方法而言，很多方面都存在弊端.现有方法都是对原始数据进行数据清洗后，再在完备数据上进行压缩和查询，然而对海量数据的清洗存在清洗代价大、清洗结果不准确以及时效性差等问题.因此，本文提出AQ-MI方法，越过数据清洗直接对海量不完整数据进行压缩和查询，该方法可以快速地定位查询数据的压缩位置，提高查询效率，还能够大幅度地减少存储空间，并且保证查询结果的完整性.

2定义和数据结构

2.1相关定义

由于对海量数据的操作需要较高的时间和空间代价，因此有查询类型少、查询语句简单固定、更新和删除频率低等特点.我们的目的是改善使用频繁的数据操作的响应时间.假设对于一个海量数据库应用，经过统计后可以获得频繁使用的数据操作语句，即查询语句中WHERE后出现的查询条件，将这些查询条件分为确定性查询条件和不确定查询条件.

定义1. 确定性查询条件Def_Query.查询下发前已经确定的查询条件，一般为频繁使用的固定范围查询，这类查询大多是查询某一属性值是否超过设定的阈值，如“Temperature>35”.确定性查询条件的属性名和属性值固定，作为一个整体出现.

定义2. 不确定查询条件Undef_Query.查询下发前不能完全确定的查询条件，一般为频繁使用的不固定等值查询，这类查询大多是查询某一属性值是否存在于记录中，如“Username=***”.不确定查询条件的属性名固定，属性值可变.

2.2基本数据结构

经过统计获得所有确定性查询条件和不确定查询条件后，在压缩存储时将每一条元组所满足的不确定查询条件的属性值和确定性查询条件作为索引存储于数据库中，同时将元组存放到相应的待压缩缓存块中.当某一缓存块装满后，将其按顺序进行压缩存储，并在数据库中存储元组所在压缩文件地址.索引表结构和压缩文件地址表结构分别如图1和图2所示:

Fig. 1　Structure of index table.图1　索引表结构

Fig. 2　Structure of compressed file address table.图2　压缩文件地址表结构

图1中，Id为索引序号，Tp_Id为元组序号，字段Undef_Val_i为当前元组第i个不确定查询条件的属性值.字段Def_Query以位编码形式存储当前元组所满足的确定性查询条件.对于n个确定性查询条件Q1,Q2,…,Qn，设当前元组的字段Def_Query的位编码为B1B2…Bn，若当前元组满足条件Qi，则Bi=1；否则Bi=0.

图2中，Block_Id为当前元组所在缓存块的序号，字段Address为缓存块压缩后对应的压缩文件地址.

通过将索引表和地址表在属性Block_Id上的连接便能够得到完整的索引文件.值得注意的是，不同Def_Query值对应不同的缓存块，也就对应不同的压缩文件地址.而当某一缓存块压缩存储后，将为Block_Id赋一个新的值，因此相同的Def_Query值也可能对应不同的缓存块和压缩文件地址.

3基于压缩的海量不完整数据近似查询算法

3.1不完整数据的标记

传统的数据清洗方法很难将不完整数据彻底清洗干净，还会造成信息损失，降低效率.因此，我们希望不对原始数据清洗，直接进行存储和管理，以此来避免信息的损失.实际上，只要能在数据库中把完整的和不完整的分量标识出来，并在查询回答中正确地保持标识，那么无论是完整的还是不完整的信息，只要它符合查询条件，都将保留在查询结果中，信息丢失问题自然不存在.

根据上述思想，在预处理阶段，扫描一次原始数据D，将属性值缺失的字段用“*”进行标记，标记后的数据记为D*.一个简单例子如表1所示，用标记“*”来区分数据库的完整和不完整分量.

Table 1Area Temperature Information Table with “*” Mark

表1　用“*”标记的地区温度信息表TempInfo

假设查询语句:

SELECTPlace,Temperature,Duration

FROMTempInfo

WHERETemperature>19

ANDDuration>8.

则查询结果如表2所示：

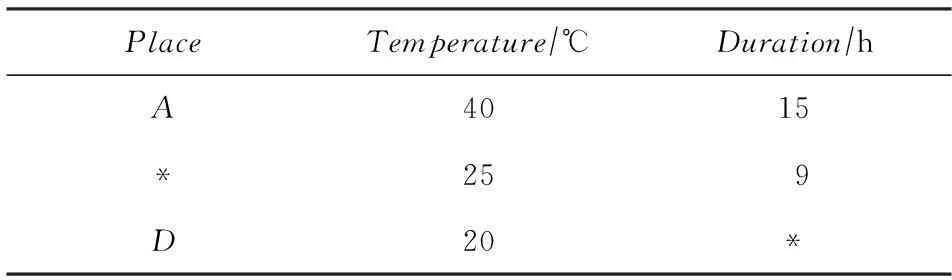
Table 2　Query Result

如表2所示，被“*”标记的字段为属性值缺失字段，它可以满足任何查询条件，因此在查询计算中可以正确地保持标记语义，使得查询结果可信有意义.

3.2D*数据的压缩存储

在对原始数据扫描标记后，获得D*数据，根据统计的频繁查询条件压缩数据至不同压缩文件并建立对应索引，然后压缩索引文件来进一步节省存储空间.因此，在压缩存储阶段，分为对D*数据的压缩和对索引文件的压缩.

3.2.1D*数据的压缩

对于海量不完整数据D*，假设D*包含m条元组，n个属性.进行压缩处理后，得到索引文件和压缩数据.假设索引文件包含i条元组、j个属性，则i≥m且j≼n.图3是D*数据的压缩示意图：

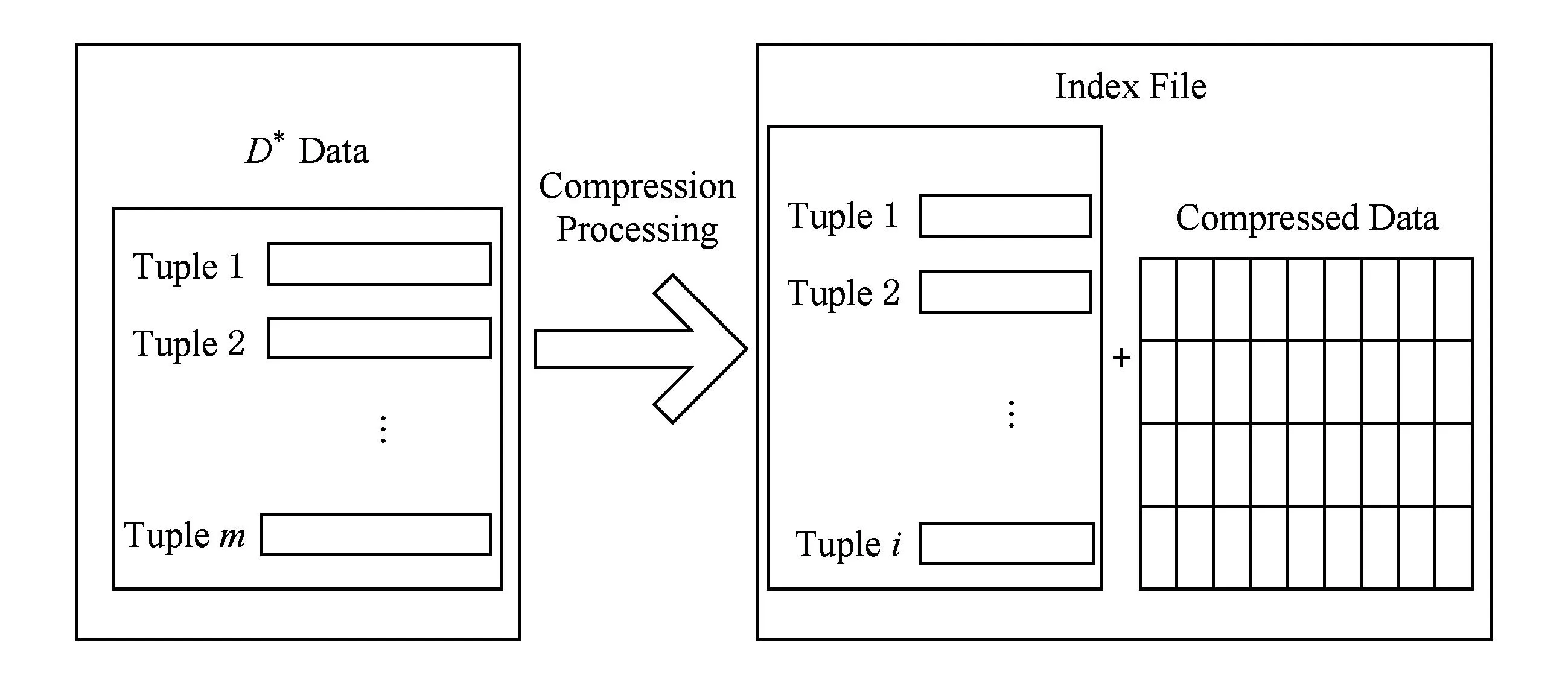
Fig. 3　The process of D*data compression.图3　D*数据压缩示意图

对于D*的每一条元组t，首先计算t所满足的确定性查询条件的Def_Query值，将t写入为该Def_Query分配的待压缩缓存块BlockDef_Query中，然后将t的不确定查询条件的属性值Undef_Vals和Def_Query作为索引项存储于数据库索引表中，同时在索引表中记录元组t所在的待压缩缓存块BlockDef_Query的序号Block_IdDef_Query.若缓存块BlockDef_Query已满，则采用某一压缩算法对BlockDef_Query进行压缩.在压缩存储的同时，将获得该压缩文件的地址AddressDef_Query，最后把Block_IdDef_Query和AddressDef_Query序对写入地址表.下面举一个简单的例子，如表3所示：

Table 3　Area Temperature Information Table

表3为地区温度信息表，假设不确定查询条件为Place=***；确定性查询条件为Temperature>35，Duration>5.则经过计算可得元组1的Def_Query值为10，元组2的Def_Query值为01.因此这2条记录将分别压缩至2个压缩文件，它们的索引表和地址表连接后所得索引文件内容如表4所示.

Table 4　Example 1 of Index File

对于标记为“*”的属性值缺失字段，它可能是任何值，那么就应该满足任何查询条件，为了保证查询结果可信有意义，需要对含有属性标记有“*”的元组进行重复压缩.即对于含有“*”标记字段的元组t，可能会计算得出2个甚至多个Def_Query值，则需要将t分别写入为这些Def_Query值分配的多个待压缩缓存块BlockDef_Query中，后续的处理过程同未含有标记字段的元组.

对表3的例子进行修改，如表5所示：

Table 5Area Temperature Information Table with “*” Mark

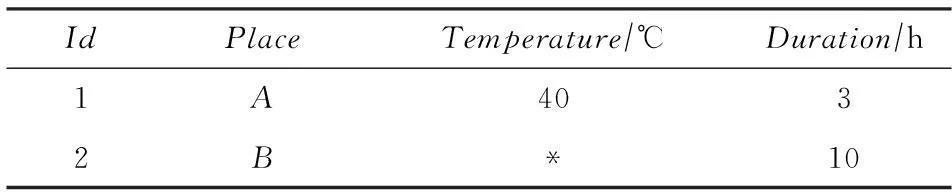
表5　用“*”标记的地区温度信息表

如果将上述例子中的信息表修改为如表5所示，则元组2的Def_Query值为01或者11，因此需要将该元组同时压缩至01和11对应的2个压缩文件中.其索引文件如表6所示：

Table 6　Example 2 of Index File

3.2.2D*数据的压缩优化

在统计确定性查询条件时，可能会出现许多冗余条件，比如经统计，频繁使用的查询条件有：Temperature>35和Temperature>55.如此将会使得索引表中属性Def_Query的位编码字段长度增加1 b，那么多个条件的集合对应的位编码将会更加冗余.如此一来，不仅会增加索引文件的存储空间，还会降低查询计算的效率.

针对这个问题，本文的优化策略是将有包含关系的确定性条件进行削减，剔除掉被包含的条件，只保留最大满足条件.如上述例子的2个条件，只保留Temperature>35.这将大大减少索引编码的长度，节省了存储空间，同时，在查询索引匹配时效率也将更高.虽然这样处理会使得最终的查询结果是近似的(包含精确结果)，但对于海量数据而言，快速地返回满足需求的近似结果是值得提倡的[13].

3.2.3基于Attr-1的索引文件压缩

根据D*数据的压缩过程可知，为了提高查询效率，D*数据的每个元组都建立了一条或多条索引，不仅如此，索引表的字段Undef_Val_i数量未知，它是由不确定查询条件来确定的，因此索引表可能是一张宽表，如此不论是从元组数量还是从属性数量上都增加了额外的存储空间.为了进一步减少存储空间，对索引文件进行压缩.而为了不增加除了D*数据查询时的解压耗时，对索引文件采用编码字典方式进行压缩，以便后期的无解压查询.

对于D*数据的索引文件T，假设T包含n个属性，共有m条元组.对于属性Ai中出现的所有候选值，按照压缩模式中Ai对应的编码模式调用不同的编码方法.T中所有属性经压缩处理后，得到编码字典和索引压缩文件.图4是索引文件的压缩示意图：

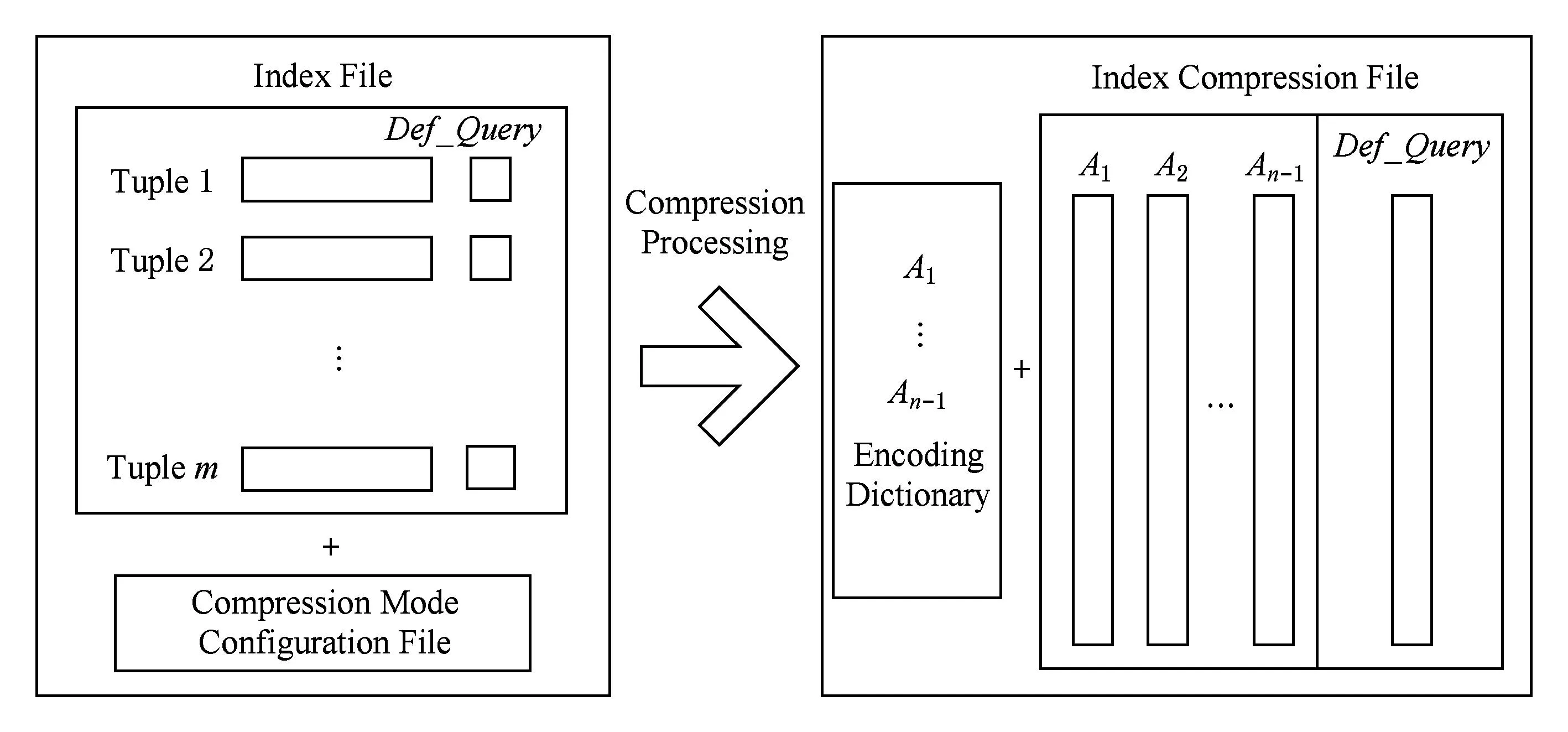
Fig. 4　The process of index file compression.图4　Attr-1索引文件压缩示意图

如图4所示，索引文件中属性Def_Query的值已经是位编码类型，因此无需对该属性进行压缩编码，仅仅对索引文件表的其他Attr-1个属性依据压缩模式配置文件进行编码，而属性Def_Query的所有数据则直接拷贝到索引压缩文件末尾，即属性Def_Query对应的数据不出现在编码字典中.

在压缩编码时候，不同属性可以采用不同的编码方式，而且还要兼顾存储空间和查询效率，因此采用K-of-N编码(K-of-Nencoding)[14].假设压缩模式配置文件规定索引文件的全部属性(除Def_Query)的编码方式皆为K-of-N编码，对表6所示的索引文件进行压缩编码，得到的编码字典如表7～11所示：

Table 7　Example of Encoding Dictionary for Id

Table 8　Example of Encoding Dictionary for Tp_Id

Table 9　Example of Encoding Dictionary for Place

Table 10　Example of Encoding Dictionary for Block_Id

Table 11　Example of Encoding Dictionary for Address

表6所示的索引文件压缩后对应的索引压缩文件如表12所示：

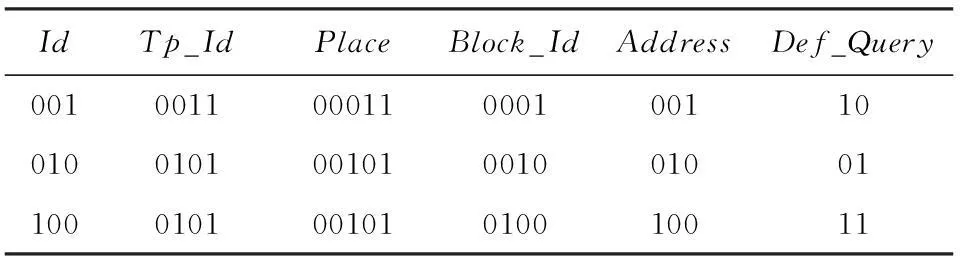
Table 12　Example of Index Compression File

表7至表12的例子只是为了解释压缩原理，并不能很好地显示出压缩效果.而实际中的数据值往往占据很大的存储空间，比如某字段值为@addr4031331963，此时将其压缩编码为001就会明显显示出压缩的效果.

3.2.4海量不完整数据D*压缩算法

如算法1所示为海量不完整数据D*的压缩算法，压缩过程包括2个阶段:1)将不完整数据D*根据确定性和不确定查询条件进行压缩并建立对应的索引;2)通过压缩模式配置文件对阶段1生成的索引文件进行压缩，以进一步减少存储空间.

算法1. 海量不完整数据D*压缩算法.

输入:海量不完整数据D*、索引压缩模式配置文件C;

输出:压缩数据K、索引压缩文件T、编码字典M.

① for each元组t∈Rdo

② if (t不包含被标记字段)

③ 计算t所满足的确定性查询条件的Def_Query值;

④ 将t写入为该Def_Query分配的待压缩缓存块BlockDef_Query中，设定其序号为Block_IdDef_Query;

⑤ else

⑥ 计算t所满足的多个Def_Query值;

⑦ 将t重复写入这些Def_Query对应的待压缩缓存块BlockDef_Query中，设定其序号为Block_IdDef_Query;

⑧ end if

⑨ 将t的不确定查询条件的属性值Undef_Vals，Def_Query，Block_IdDef_Query插入数据库索引表;

⑩ if (BlockDef_Query已满)

根据算法1的描述可知，阶段1以元组为单位对D*数据进行计算并进行压缩，因此时间复杂度为O(N)；阶段2分别以属性和元组为单位，对索引文件进行了一次扫描，2次扫描分别生成了编码字典和索引压缩文件，因此时间复杂度为O(N).所以，海量不完整数据D*的压缩算法时间复杂度为O(N).

3.3压缩后D*数据的近似查询

3.3.1近似查询

所谓近似查询，体现在2个方面：1)在统计频繁确定性查询条件时，为了节省存储空间并且提高查询效率，将被包含的确定性条件剔除，如此在查询时便会得到包含精确结果的近似查询结果；2)在查询结果中带有*标记的不完整数据.由于索引的存在可以快速获得满足查询条件的压缩文件地址集合，因此在查询处理阶段，主要工作就是对索引压缩文件的无解压查询，其本质就是通过对查询语句的解析，将对原始数据的查询转化为对压缩编码位的选择和投影操作.

3.3.2选择操作

基于本文提出的压缩和查询处理方法的特殊性，在无解压查询时可能涉及到的选择操作仅是对属性Undef_Vals和属性Def_Query的等值操作，因此对其他操作不做赘述.依旧以K-of-N编码为例，假设要进行的等值操作为Undef_Val_i=X，X的编码为xnxn-1…x2x1，待比较数据的编码为anan-1…a2a1.等值操作规则如下：

K-of-N编码由于采用了N位中有K位为1的规则，因此只需要知道这些为1的编码位具体是哪些位，就可以唯一地确定一个编码.假设X的编码xnxn-1…x2x1中，xi1xi2…xik为编码为1的位，则在待比较的编码中，只有编码ai1ai2…aik对应的编码也全部为1，才是和B相等的数据.该操作要处理的编码位为K位，以上过程可形式化地表示为

(1)

同理可得不等值操作的形式化表示为

(2)

需要注意的是，属性Def_Query本身就是位编码形式，因此K-of-N编码的选择操作规则不适用于属性Def_Query.因为Def_Query的值是由若干确定性查询条件生成的，所以需要比较每一位才能知道是否等值.假设要进行的等值操作为Def_Query=X，X的编码为xnxn-1…x2x1，待比较数据的编码为anan-1…a2a1.等值操作规则如下：

对于待比较编码anan-1…a2a1，如果其上所有编码位上的编码与X的编码xnxn-1…x2x1一一对应地全部相同，那么该编码就与X的编码相等.操作规则形式化描述为

(3)

同理可得不等值操作的形式化表示为

(4)

3.3.3投影操作

由于采用了按列压缩和存储的基本思想，因此对索引压缩文件的投影操作相对来说比较简单.投影操作在所有的选择操作结束后执行，选择操作结束后获得满足选择条件的元组集合.对于索引压缩文件来说，仅是对属性Address进行投影操作，因此，对于元组集合中的每一条元组对应的属性Address，在编码字典中查找对应的原始数据值，在这些原始值集合中去掉重复的数据，就得到投影操作的最终结果.

3.3.4海量不完整数据D*查询算法

在进行无解压查询时，需要由查询条件来构造查询索引.查询索引构造方法如下：首先分析查询语句，将其查询条件用不确定查询条件和位编码形式的确定性查询条件来表示.如此，原查询语句的查询条件就转化为由Undef_Query和Def_Query组成的查询索引.

如果查询索引中只存在Def_Query，则直接以Def_Query对索引压缩文件进行选择操作，对得到的选择结果在属性Address上做投影操作即可得到满足查询条件的D*数据的压缩地址集合，根据地址集合解压文件后即可得到查询结果.如果查询索引中存在Undef_Query，则需要在编码字典中找到Undef_Query对应的编码，然后对索引压缩文件进行后续操作.海量不完整数据D*查询算法如算法2所示：

算法2. 海量不完整数据D*查询算法.

输入:查询语句Q、编码字典M、索引压缩文件T、压缩数据K;

输出:查询结果Result.

① 解析查询语句Q，得到Undef_Query和Def_Query构造查询索引X;*选择操作*

② if (Undef_Query≠Null)

③ for eachUndef_Val∈Undef_Querydo

④ 在编码字典M中查找对应的编码;

⑤ 采用式(1)(2)对T进行选择操作;

⑥ end for

⑦ end if

⑧ if (Def_Query≠Null)

⑨ 采用式(3)(4)对T进行选择操作;

⑩ end if

根据算法2的描述可知，在选择操作中，最好情况下对Def_Query进行选择操作，时间复杂度为O(1)；最坏情况下对Undef_Query中的多个条件进行选择操作，时间复杂度为O(N)，因此选择操作时间复杂度为O(N).在投影操作中，需要对编码字典进行一次扫描，所以投影操作时间复杂度为O(N).最后根据查询到的地址集合将查询结果依次解压出来，时间复杂度为O(N).所以，海量不完整数据D*的查询算法时间复杂度为O(N).

3.4不完整数据多重压缩的优化

根据2.2.1节的描述，在对含有*标记的属性的元组进行压缩的时候，会涉及到同一元组的多重压缩.在只有1个*属性满足确定性查询条件的情况下，该元组重复压缩至2个压缩文件；2个*属性分别满足2个确定性查询条件时，将增加至4个压缩文件,如此便呈现指数增长，将会大大增加压缩的代价.

针对这个问题，本文采用基于属性重要性的主客观权重分配策略.在对原始数据进行压缩存储之前，首先对全部属性进行主观权重分配并设定阈值，即根据专家经验主观评估各属性之间的相对重要程度，相对重要的属性分配相对较高权重.设定阈值为γ，则权重大于γ的属性为重要属性.在压缩阶段，只有当*标记的属性权重大于阈值时才进行多重编码，否则只对元组编码一次即可.

每次查询之后，对查询结果的属性进行客观权重分配并反馈给初始主观权重进行调整.假设查询结果为n个属性对应的m条元组记录，则大体过程如下.

1) 采用m×n阶特征值矩阵对查询结果进行聚类如式(5)所示：

(5)

2) 计算得到特征值矩阵的*余子式，保证数据集的完备性；

3) 采用最大最小法建立模糊相似关系如式(6)所示：

(6)

4) 利用模糊等价闭包法求出模糊等价矩阵并确定分类数目；

5) 依次求出删除各属性后的分类数目以确定各属性的重要性；

6) 根据重要性的大小确定各属性的权重分配，若某属性删除后分类数目没有发生变化，则表明该属性在查询结果的整体性评价中是不必要的；

7) 将本次查询得到的部分属性客观权重反馈给初始主观权重进行动态调整，以便于新增数据的压缩优化.

采用基于属性重要性的主客观权重分配策略将在很大程度上减少压缩耗时以及存储空间，同时也保证了重要属性在查询结果中的正确性和完整性.

4实验及其分析

本节通过实验来验证本文提出的基于压缩的不完整数据近似查询方法AQ-MI的性能.实验主要分为压缩率实验、查询效率实验、优化对比实验和信息丢失比实验4个部分.将AQ-MI与压缩处理技术中典型的字典压缩算法LZW[9]和索引压缩算法PI[11]在压缩率以及查询效率2方面进行了对比分析，又将AQ-MI与数据清洗技术中典型的基于元组删除法RWD[4]和基于数据填充法MIBOI[5]在查询结果信息丢失比例方面进行了对比分析，最终给出实验结果.

4.1实验设置

本实验中采用的数据为TPC-H Benchmark[15]生成工具DBGen生成的Lineitem表.DBGen按照主键L_OrderKey值递增顺序产生带有随机属性值缺失字段的Lineitem记录.

4.2压缩率实验

在这个实验中，采用压缩率(compression rate,CR)来衡量不同方法的压缩效果.首先对压缩率进行如下定义：压缩率即压缩后数据与压缩前数据的比值.

由CR定义可知，CR越小说明压缩效果越好.设定Lineitem表的属性数量固定为16，记录数量不断增加.3种压缩方法的CR如图5所示:

Fig. 5　Experiment result of CR.图5　CR实验结果图

图5显示了3种压缩方法的CR.从图5中可以看出，CR与数据大小的变化没有什么明显的关系，随着原始数据从100 MB增大至2 GB，各个压缩方法的CR基本保持稳定.由CR定义可知各个压缩方法的CR公式：

CRPI=(索引文件大小+压缩数据大小)原始数据大小；

CRLZW=(编码字典大小+压缩数据大小)原始数据大小；

CRAQ-MI=(编码字典大小+索引压缩文件大小+压缩数据大小)原始数据大小.

显然地，PI的CR最大，其次是AQ-MI和LZW.这是由于PI将原始数据压缩的同时建立了索引文件，虽然这样能够提升查询效率，却增加了额外的存储空间.而LZW压缩效果最佳，这是因为它压缩后的数据仅仅多了一个编码字典.本文提出的AQ-MI比LZW多出一个索引压缩文件，因此CR稍大，但是仅仅牺牲一点存储空间却换来了查询效率的提高是值得的.

4.3查询效率实验

在这个实验中，对3种压缩方法的压缩数据进行查询的效率测试，即查询时间测试.主要考察在数据大小固定时，3种方法分别进行压缩后数据的查询执行情况，以验证各个算法的实时性能.设定Lineitem表的记录数量固定为700万条，大小为1 GB，查询条件数量不断增加.3种方法的查询效率如图6所示：

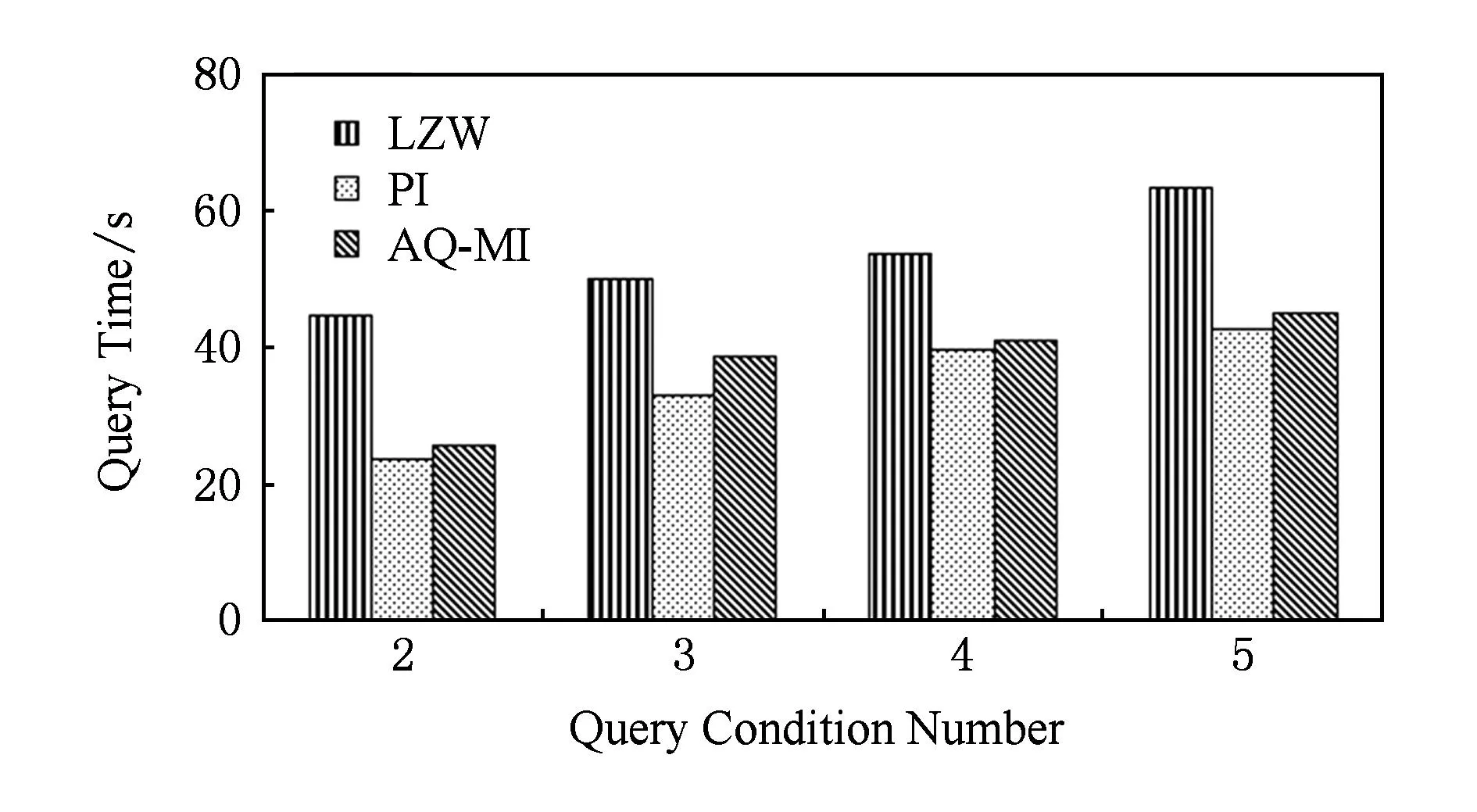
Fig. 6　Experiment result of query efficiency.图6　查询效率实验结果图

图6显示了3种压缩方法将1 GB的原始数据压缩后，在不同查询条件数目下的查询时间.从图6中可以看出，随着查询条件数量从2个增加到5个，各方法压缩后数据的查询时间都在增加.其中，LZW的查询时间最长，其次是AQ-MI和PI.这是因为LZW在查询时需要先分析查询条件，然后对压缩数据做选择和投影操作，其查询时间会随着操作条件的增加而增加.PI在压缩时就建立了对应压缩地址的索引，分析并得到满足查询条件的索引，就可以快速地返回查询结果.本文提出的AQ-MI比PI多了一步无解压查询索引压缩文件，虽然也需要做选择和投影操作，但不论查询条件数量多少，大多数情况下仅需要对属性Def_Query做一次选择操作，对属性Address做一次投影操作即可，然后得到D*数据压缩地址就可以快速返回查询结果.

4.4优化对比实验

在这个实验中，对本文所提方法AQ-MI和优化后方法AQ-MI′进行对比测试.主要考察采用压缩优化策略前后的压缩效果.设定Lineitem表的属性数量固定为16，记录数量固定为700万条，大小为1 GB，Def_Query数量不断增加.AQ-MI和AO-MI′的CR如图7所示：

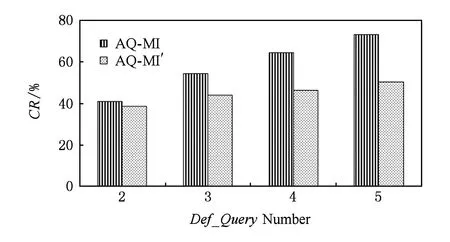
Fig. 7　Experiment result of optimization comparison of CR.图7　CR优化对比实验结果图

图7显示了AQ-MI和AO-MI′的CR.从图7可以看出，随着Def_Query数目从2个增加到5个，AQ-MI和AO-MI′的CR都在增大，但是显然AQ-MI的CR增长幅度更大，这是因为AQ-MI在对含有*标记的属性的元组进行压缩的时候，只要有1个*属性满足Def_Query，就会让该元组的压缩次数增加1倍，虽然属性值缺失字段是随机产生的，CR并不会呈现指数增长，但Def_Query数量的增多自然会导致压缩效率的降低.相对地，AQ-MI′的CR虽然也在增长，但明显远远低于AQ-MI，这是由于其采用了基于属性重要性的主客观权重分配策略，权重高于阈值的属性仅仅是少数，CR自然就比AQ-MI低了.查询同理，CR低，索引文件的元组数量就少，从而减少了查询时的投影操作以及字典匹配操作，查询效率自然就高，这里不再赘述.在实际应用中，对海量数据的操作需要较高的时间和空间代价，一般情况下查询类型较少，而本文的压缩优化正适用于数据量大，确定性查询条件多的情况，且Def_Query数目越多优化效果越明显.

4.5信息丢失比实验

在这个实验中，采用信息丢失比(information loss ratio,ILR)来对本文提出的AQ-MI方法和主流数据清洗方法RWD，MIBOI在信息保持方面的性能进行比较.首先对信息丢失比进行如下定义：所有满足查询条件但丢失的属性值所有满足查询条件的属性值.

由ILR定义可知，ILR越小说明信息保持性能越好.设定对Lineitem表的查询条件不变，数据记录数量不断增加.3种方法的ILR如图8所示：

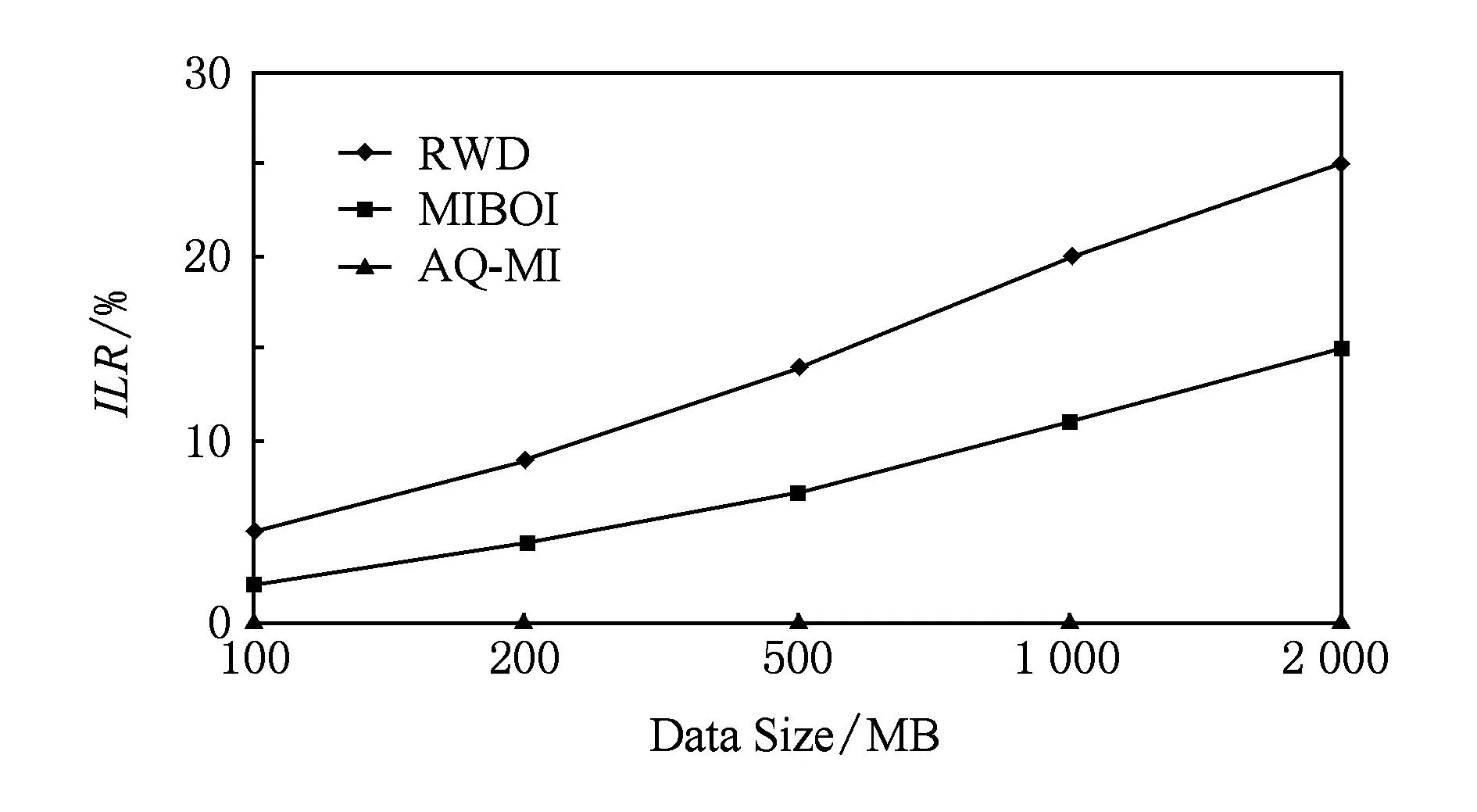
Fig. 8　Experiment result of ILR.图8　ILR实验结果图

图8显示了3种方法的ILR.从图8中可以看出，随着原始数据从100 MB增大至2 GB，RWD查询结果的ILR最高，其次是MIBOI，而本文提出的AQ-MI没有信息丢失.这是因为RWD是基于记录删除的清洗方法，在查询之前将属性值缺失的记录删除，这样虽然能查询得到唯一确定的结果，但是丢失了很多有价值的信息，尤其是在原始数据中含有很多不完整数据的情况下丢失比更大.MIBOI是基于数据填补的清洗方法，在查询预处理阶段是以不完备数据聚类的结果为基础进行缺失数据的填补，虽然能够得到一个完备的信息表，但一些填补的数据不一定符合客观事实，即与缺失的真实数据不一致，这就可能导致查询结果缺少了本该包含的信息，但至少它的ILR比直接删除记录的RWD要低很多.而本文提出的AQ-MI方法在预处理阶段只是扫描数据库并标记属性值缺失字段，在后续的压缩存储过程中，对有标记字段的元组进行多重压缩，保证了查询结果的完整性和可信性.

5结束语

传统的数据修复方法对于海量数据处理代价过高，且不能彻底修复，为了实现在不完整的海量数据上进行满足给定需求的近似查询，提出了一种基于压缩的海量不完整数据近似查询方法AQ-MI.该方法对属性值缺失字段进行标记，根据频繁查询条件对标记后的数据进行压缩，并建立对应索引；根据属性划分对索引文件再次压缩以节省存储空间，采用编码字典对索引压缩文件进行选择和投影操作，最终获得不完整数据的近似查询结果.实验表明:与现有的压缩查询处理方法相比，AQ-MI不仅能在很大程度上减少存储空间，还能够提高查询效率.此外，它对不完整信息的处理与现有的数据清洗方法相比，更能保证查询结果的完整性.

参考文献

[1]Li Jianzhong, Liu Xianmin. An important aspect of big data: Data usability[J]. Journal of Computer Research and Development, 2013, 50(6): 1147-1162 (in Chinese)(李建中, 刘显敏. 大数据的一个重要方面: 数据可用性[J]. 计算机研究与发展, 2013, 50(6): 1147-1162)

[2]Aste M, Boninsegna M, Freno A, et al. Techniques for dealing with incomplete data: A tutorial and survey[J]. Pattern Analysis and Applications, 2015, 18(1): 1-29

[3]Dai J. Rough set approach to incomplete numerical data[J]. Information Sciences, 2013, 241(12): 43-57

[4]Kolahi S, Lakshmanan L V S. On approximating optimum repairs for functional dependency violations[C]Proc of the 12th Int Conf on Database Theory. New York: ACM, 2009: 53-62

[5]Wu Sen, Feng Xiaodong, Shan Zhiguang. Missing data imputation approach based on incomplete data clustering[J]. Chinese Journal of Computers, 2012, 35(8): 1726-1738 (in Chinese)(武森, 冯小东, 单志广. 基于不完备数据聚类的缺失数据填补方法[J]. 计算机学报, 2012, 35(8): 1726-1738)

[6]Chen Zhikui, Lü Ailing, Zhang Qingchen, et al. A new algorithm for imputing missing data based on distinguishing the importance of attributes[J]. Microelectronics and Computer, 2013, 39(7): 2630-2631 (in Chinese)(陈志奎, 吕爱玲, 张清辰. 基于属性重要性的不完备数据填充算法[J]. 微电子学与计算机, 2013, 39(7): 2630-2631)

[7]Chen Yuxin, Cheng Xu, Zhao Peng, et al. Process missing information for massive sparse data storage in cloud environment[J]. Journal of Computer Research and Development, 2012, 49(Suppl): 316-322 (in Chinese)(陈郁馨, 程序, 赵鹏, 等. 云环境中一种面向海量稀疏数据存储的缺失值处理方法[J]. 计算机研究与发展, 2012, 49(增刊): 316-322)

[8]Xu Xia, Ma Guangsi, Yu Tao. Research and improvement on LZW lossless compression algorithm[J]. Computer Technology and Development, 2009, 19(4): 125-127 (in Chinese)(许霞, 马光思, 鱼涛. LZW无损压缩算法的研究与改进[J]. 计算机技术与发展, 2009, 19(4): 125-127)

[9]Nandi U, Mandal J K. Modified compression techniques based on optimality of LZW code (MOLZW) [J]. Procedia Technology, 2013, 10: 949-956

[10]Liang Huaguo, Jiang Cuiyun, Luo Qiang. Test data compression and decompression using symmetry-variable codes[J]. Journal of Computer Research and Development, 2011, 48(12): 2391-2399 (in Chinses)(梁华国, 蒋翠云, 罗强. 应用对称编码的测试数据压缩解压方法[J]. 计算机研究与发展, 2011, 48(12): 2391-2399)

[11]Zhao Kai, Li Jianzhong, Luo Jizhou. Storage and operation of massive data compression based on predication index[J]. Computer Science, 2005, 32(9): 86-90 (in Chinese)(赵锴,李建中,骆吉洲. 基于谓词索引的海量数据压缩存储及数据操作算法[J]. 计算机科学, 2005, 32(9): 86-90)

[12]Arenas M, Pérez J, Reutter J. Data exchange beyond complete data[J]. Journal of the ACM, 2011, 60(4): 83-94

[13]Nair R. Big data needs approximate computing: Technical perspective[J]. Communications of the ACM, 2014, 58(1): 104-104

[14]Wong H K T, Liu H F, Olken F, et al. Bit transposed files[C]Proc of the 11th Int Conf on VLDB. San Francisco: Morgan Kaufmann, 1985: 448-457

[15]Transaction Processing Performance Council(TPC). TPC BENCHMARKTMH (Decision Support) Standard Specification Revision 2.17.1[EBOL]. (2014-11-13) [2015-05-13]. http:www.tpc.orgtpchdefault.asp

Wang Yan, born in 1978. PhD candidate and associate professor. Student member of China Computer Federation. Her main research interests include massive data query technology, sensing data processing, big data management, etc.

Liu Genghao, born in 1990. Master candidate. Student member of China Computer Federation. His main research interests include massive data query technology, etc.

Wang Junlu, born in 1988. Master and assistant engineer. Student member of China Computer Federation. His main research interests include database theory and techniques, big data processing techniques and massive data processing techniques, etc.

Song Baoyan, born in 1965. PhD and professor. Senior member of China Computer Federation. Her main research interests include database theory and techniques, RFID event stream processing techniques, big data management and graph data management, etc.

中图法分类号TP391

通信作者：宋宝燕(bysong@lnu.edu.cn)

基金项目：国家自然科学基金项目(61472169,61472072)；国家科技支撑计划基金项目(2012BAF13B08)；国家“九七三”重点基础研究发展计划前期研究专项基金项目(2014CB360509)；辽宁省科学事业公益研究基金项目(2015003003)；辽宁省工业攻关及成果产业化计划项目(2012216007)

收稿日期：2015-06-30；修回日期：2015-11-06

This work was supported by the National Natural Science Foundation of China (61472169，61472072), the National Key Technology Research and Development Program of China (2012BAF13B08), the National Basic Research Program of China (973 Program) (2014CB360509), the Science Commonweal Research Foundation of Liaoning Province (2015003003), and the Industrial Research and Production Industrialization Program of Liaoning Province (2012216007).