布置参数对TBM边缘滚刀受力的影响

郑　聪， 赵　威， 张海丰， 马保松

(1. 中国地质大学(武汉)工程学院， 湖北 武汉　430074；

2. 中交第二公路勘察设计研究院有限公司， 湖北 武汉　430056)



布置参数对TBM边缘滚刀受力的影响

郑聪1， 赵威2， 张海丰1， 马保松1

(1. 中国地质大学(武汉)工程学院， 湖北 武汉430074；

2. 中交第二公路勘察设计研究院有限公司， 湖北 武汉430056)

摘要：边缘滚刀安装在全断面隧道掘进机(TBM)刀盘的最外缘，在破岩时边缘滚刀的受力情况十分复杂，工作条件恶劣，容易损坏。为研究布置参数对边缘滚刀的影响，采用有限元分析软件ABAQUS建立边缘滚刀破岩的非线性动力学模型，分析边缘滚刀的受力情况。结果表明： 边缘滚刀在破岩时所受的作用力会剧烈振荡变化； 安装倾角和刀盘过渡圆弧半径对边缘滚刀受力的影响显著； 边缘滚刀受力随着安装倾角和刀盘过渡圆弧半径的增加而呈现近似线性的增长。

关键词：TBM； 边缘滚刀； 安装倾角； 过渡圆弧半径； 有限元

0引言

盘形滚刀是全断面隧道掘进机(TBM)刀盘上的主要切削刀具。根据滚刀在刀盘上的安装位置，将滚刀分为中心滚刀、正滚刀和边缘滚刀。边缘滚刀安装在刀盘外缘，具有一定的安装倾角。由于其位置特殊、受力情况十分复杂、线速度大和工作条件恶劣，故边缘滚刀易损坏。对边缘滚刀破岩过程中的受力情况进行分析，可以帮助设计人员优化边缘滚刀的布置参数。

国内学者对盘形滚刀进行了大量的研究。夏毅敏等[1]采用遗传算法分析了复合式土压平衡盾构盘形滚刀布置的基本规律； 沈斌[2]从破岩机理的角度研究了滚刀破岩的关键影响因素，提出了边缘滚刀布置的优化方法； 宋克志等[3]分析了刀盘上滚刀推力分布规律，得出刀盘上不同位置的滚刀推力差异较大； 张厚美[4]总结滚刀受力的计算方法，根据各种计算方法，编写了掘进性能预测程序，用于TBM刀具布置优化； 吴元等[5]从破岩效率的角度出发，分析了边缘滚刀刀刃角等关键参数的影响。但目前研究边缘滚刀破岩过程受力变化情况的文献较少。

本文采用ABAQUS软件建立不同安装倾角和刀盘过渡圆弧半径条件下的边缘滚刀破岩的非线性动力学模型，研究不同条件下边缘滚刀所受垂直力、滚动力和扭矩的变化规律。

1边缘滚刀的位置参数及岩石模型

1.1TBM刀具类型及位置

图1为刀盘上滚刀刀具类型与安装位置示意图。边缘滚刀安装在刀盘最外缘的过渡圆弧区域，且有一定的安装倾角。边缘滚刀距离刀盘中心较远，掘进时绕刀盘中心点公转的半径较大，在破碎岩石时线速度较大，工作条件差，受力情况复杂，也更容易损坏[6-7]。边缘滚刀与正滚刀在刀盘上的分布位置及具体参数如图2所示(其中，R为过渡圆弧中心到刀盘中心轴线的距离，r为过渡圆弧半径，θ为滚刀安装倾角)。

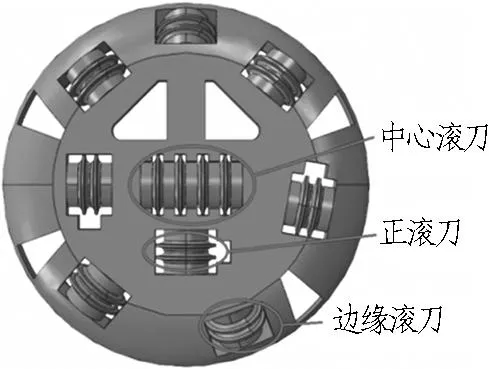
图1　滚刀刀具类型与位置示意图

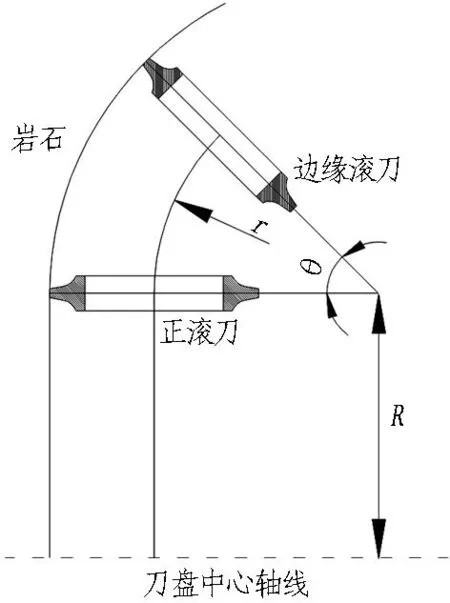
图2　边缘滚刀位置参数

1.2滚刀模型

滚刀模型采用使用最广泛的17 in盘形滚刀(半径r0=216 mm)为原型，并进行一定的简化。图3为滚刀模型剖面图。滚刀一般采用合金钢材料，其强度和硬度远大于岩石。在仿真过程中，不考虑滚刀磨损，将滚刀设定为刚体，采用各向同性的线弹性材料来模拟边缘滚刀材料。滚刀与岩石材料的各项物理力学参数见表1。

图3　滚刀模型剖面图(单位： mm)

1.3岩石模型

本文主要考虑边缘滚刀与岩石的相互作用，而边缘滚刀安装于刀盘过渡圆弧段，所以选取与刀盘过渡圆弧段相适应的具有一定厚度的弧形岩石模型。岩石材料的力学性质十分复杂，其应力应变分为3个阶段： 弹性阶段、塑性阶段和断裂损伤阶段[8]。岩石的应力-应变曲线如图 4所示：AB段材料处于弹塑性变形阶段，材料的应变不断增大，应力也不断增大； 当应力增加到B点时，即D=0时(D为损伤因子)，材料开始进入损伤阶段，材料的应变继续增大而应力逐渐减小； 直至C点，即D=1时，材料破坏

表1　滚刀与大理石材料参数

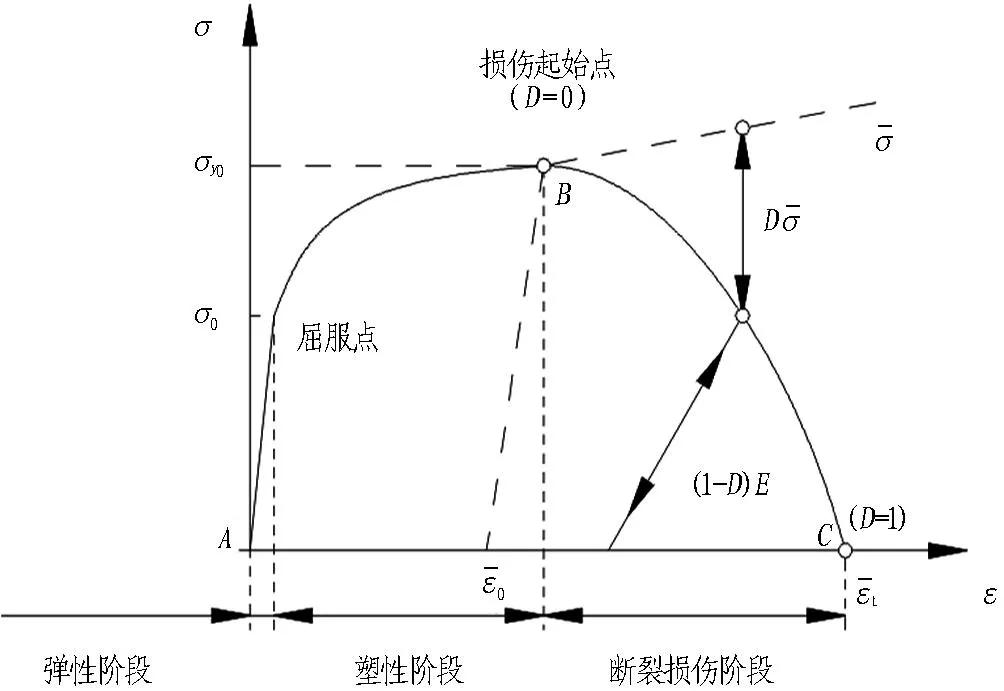
图4　岩石的应力-应变曲线

本次仿真分析中，为了较好地模拟岩石材料的塑性本构关系，依据德鲁克-普拉格塑性屈服准则，采用包含单元删除功能的损伤失效准则模拟岩石材料的屈服和破坏。扩展线性德鲁克-普拉格模型在π平面上的屈服轨迹如图 5所示，屈服函数为

F=t-ptanβ-d=0。

(1)

式中： t为偏应力； p为等效压应力； β为屈服面在p-t应力空间上的倾角，等于材料的摩擦角； d为屈服面在应力空间t轴上的截距，等于材料的黏聚力。

以大理石作为本次模拟中岩石的材料原型，大理石的物理力学参数见表1[9]。

2边缘滚刀切削岩石的动力学模型

图6为边缘滚刀破岩的动力学模型。在考虑实际工况及数值模拟效率的情况下，设定切削深度h=5mm。参考点N(如图6(b)所示)设在滚刀的质心处，建立其与整个滚刀的刚体约束关系，对N施加约束及边界条件来控制整个滚刀的运动。滚刀随切削刀盘转动时的运动轨迹是一小段圆弧，由于边缘滚刀距刀盘中心点较远，在仿真中以一小段直线代替这段圆弧，即假定滚刀的运动轨迹是直线。对N施加沿z轴负方向的平动速度v和绕自身中轴线的转动角速度ω，将其他方向的自由度全部固定。固定岩石模型中除开挖面之外的所有平面的自由度，放开开挖面的自由度。滚刀与岩石之间采用非光滑的接触来模拟，法向性质为允许分开的硬接触，切向性质为采用罚函数的摩擦算法，摩擦因数为0.325[10]。

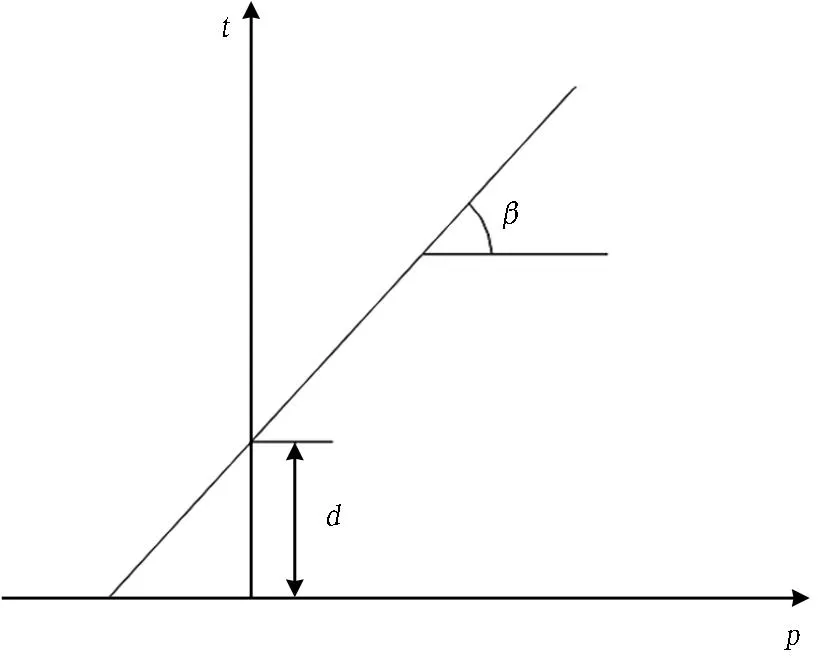
图5　扩展线性德鲁克-普拉格模型p-t关系曲线

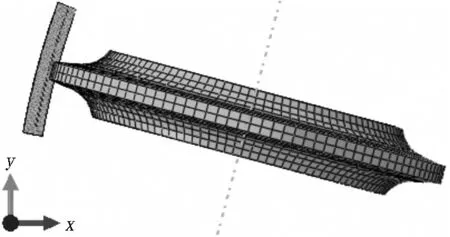
(a) 平面图

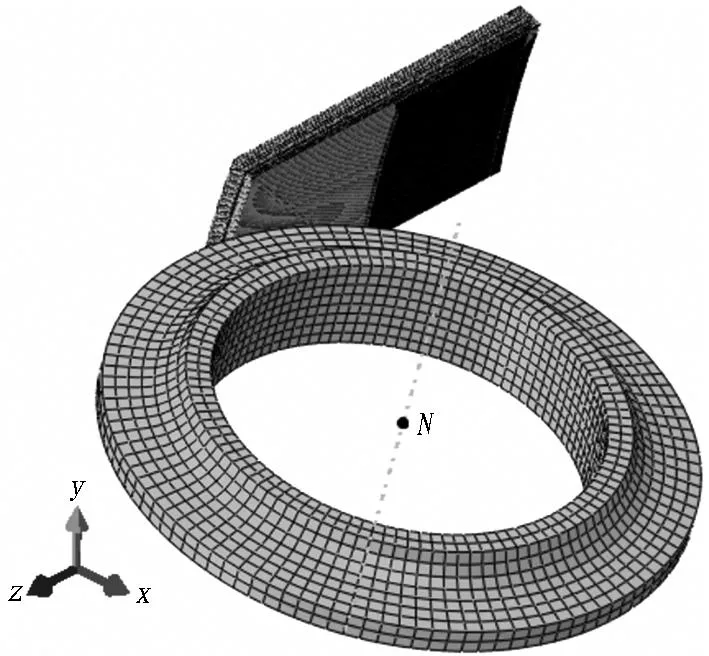
(b) 三维图

本次模拟中设定过渡圆弧中心到刀盘中心轴线的距离R=2 150mm，转速ω0=1.026 3rad/s[11]。为了研究安装倾角和刀盘过渡圆弧半径对边缘滚刀切削岩石的影响，设置4种不同的安装倾角θ=15°、30°、45°和60°及4种不同的刀盘过渡圆弧半径r=200、400、600、800mm。假定滚刀与岩石之间无相对滑移，即滚刀运动为纯滚动，由此得滚刀的平动速度v和转动角速度ω的计算表达式为：

l=R+r·sinθ;

(2)

v=ω0·l;

(3)

ω=v/r0。

(4)

式中 l为边缘滚刀中心点到刀盘轴线的距离，mm。

边缘滚刀线速度及角速度的计算结果见表 2。

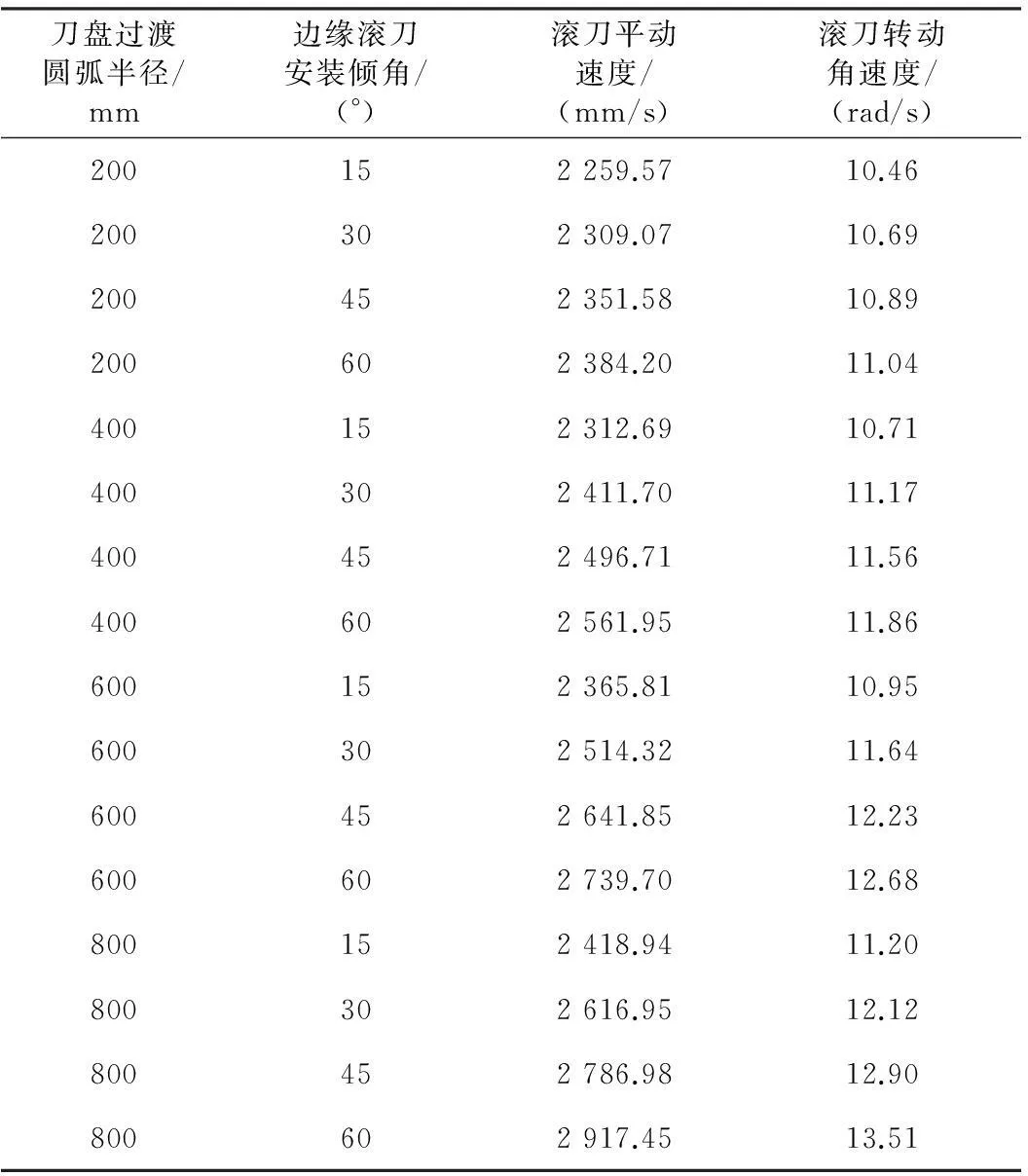
表2　边缘滚刀线速度及角速度

3模拟结果分析

3.1边缘滚刀受力动态变化

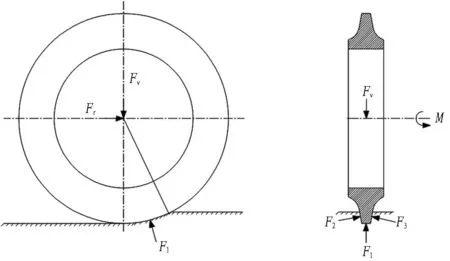
如图7所示，滚刀在沿着切削进程方向的滚动力Fr作用下向前滚动破碎岩石，在受到垂直于岩石表面方向的垂直力Fv的作用下压入岩石，并保持一定的切削深度；F1为岩石对滚刀刀刃顶部的作用力；F2和F3为岩石对滚刀刀刃侧面的作用力；M为绕滚刀轴线的扭矩。

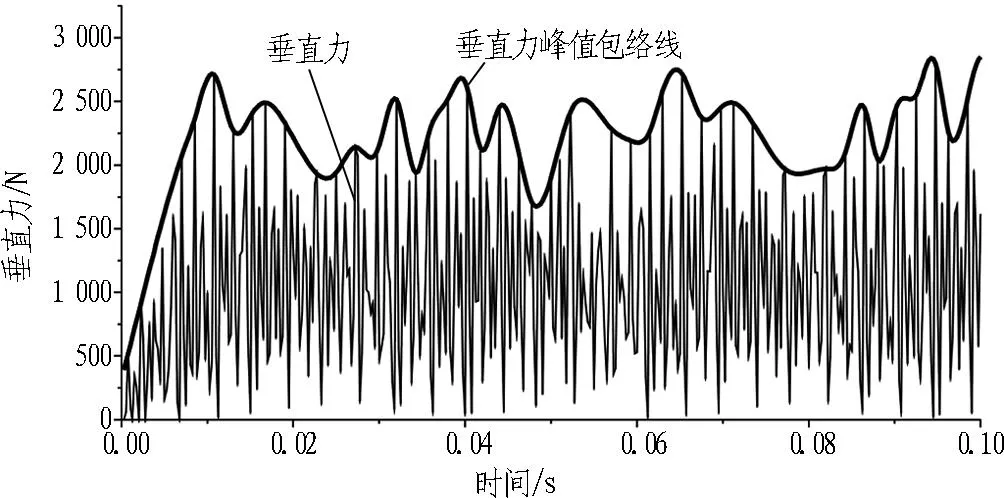
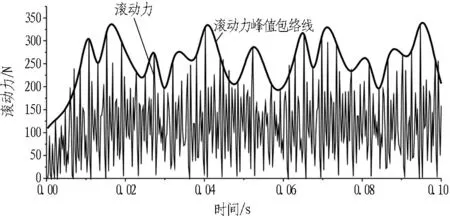
图8是过渡圆弧半径r=800 mm、边缘滚刀安装倾角θ=60°时，边缘滚刀的垂直力、滚动力和扭矩的变化情况。整个切削过程中，边缘滚刀受力是不断振荡变化的。垂直力最大值为2 595 N； 滚动力最大值为298 N，约为垂直力的1/10； 扭矩最大值为49 012 N·m。滚刀受力出现高频率的振荡，反映了切削岩石这一过程是不平稳的，这是由岩石材料的物理力学性能决定的。岩石材料与土体材料不同，其具有一定的弹脆性，塑性变形的能力较小，往往在塑性变形不大的情况下突然发生破坏。滚刀压入岩石后，岩石在外力作用下产生弹性变形，随着滚刀压入深度的不断加大，产生的弹性变形越来越大，直至岩石材料屈服进入塑性变形阶段，此阶段滚刀的受力是不断增加的。岩石材料可产生的塑性变形量很小，所以在进入塑性变形阶段之后很快会破坏，滚刀受力大幅度减小。滚刀向前移动不断切削岩石，岩石不断产生弹性变形，继而塑性变形，直至破坏，使得滚刀受力曲线在整体上出现高频率的陡增和回落。纪昌明等[12]认为滚刀破岩时，岩石的破坏具有不断阶跃破碎的特点，本文的数据结果也验证了这一点。

(a)(b)

图7滚刀受力示意图

Fig. 7Stressing of disc cutter

研究边缘滚刀破岩时的受力情况，除了应分析滚刀整体受力的振荡变化规律之外，也应当重点分析各项受力的最大值。为了分析在切削过程中的各向受力最大值的变化情况，作垂直力峰值、滚动力峰值及扭矩峰值包络线，如图8所示。垂直力峰值为1 600～2 700 N，滚动力峰值为180～330 N，扭矩的峰值为25 000～50 000 N·m。

3.2边缘滚刀受力单因素分析

在边缘滚刀的布置参数中，安装倾角和刀盘过渡圆弧半径对边缘滚刀受力的影响较大。边缘滚刀的受力情况是不断变化的，分析中应考虑整个过程中的受力平均值及受力峰值平均值。将整个受力过程中的受力取平均作为受力平均值； 取受力最大的20个峰值，将其取平均设定为受力峰值平均值。

3.2.1边缘滚刀受力与安装倾角的关系

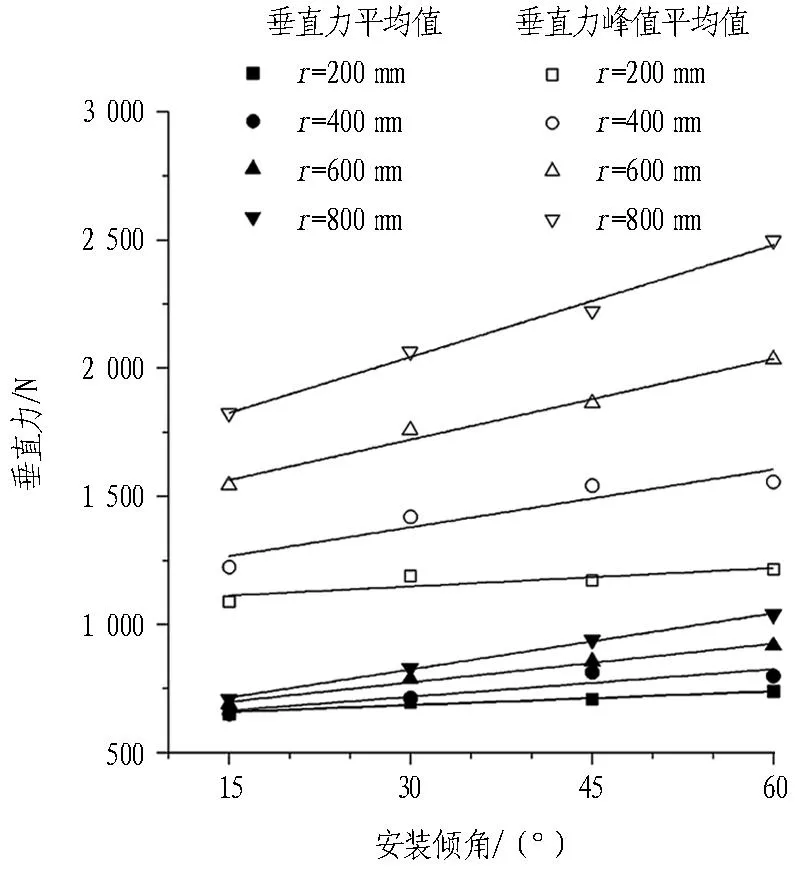
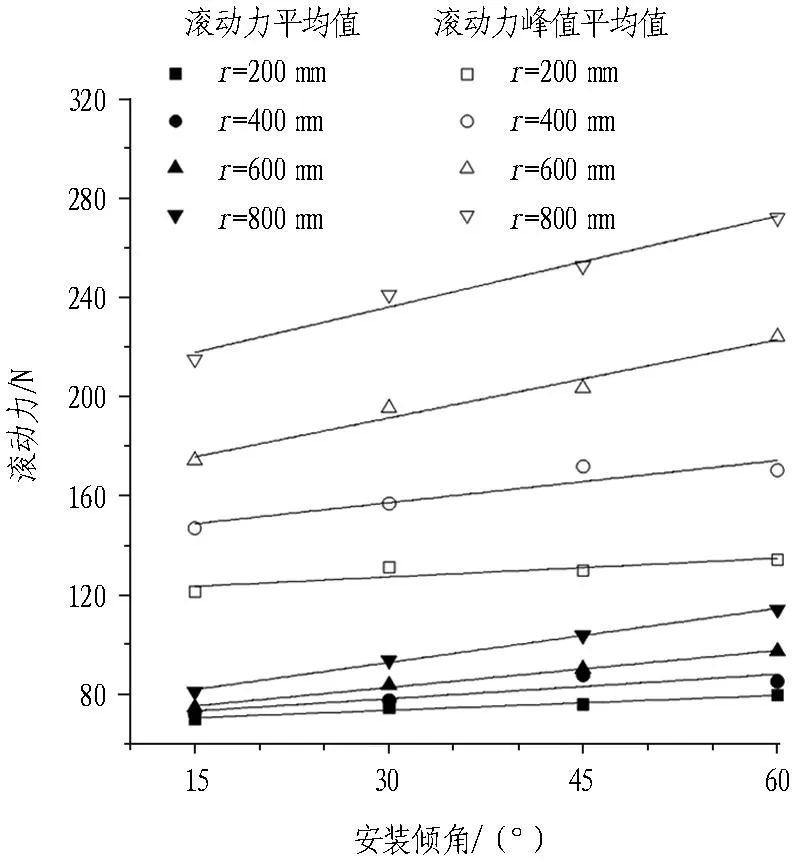
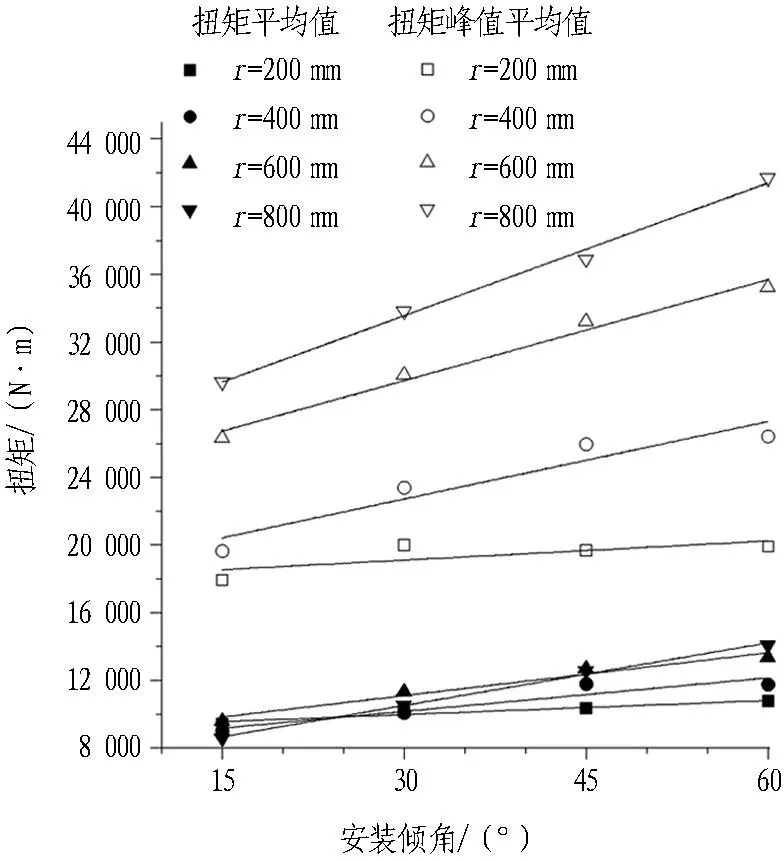
图9为边缘滚刀不同安装倾角下的垂直力、滚动力和扭矩的变化情况。从图9中可以看出，在相同的安装倾角和刀盘过渡圆弧半径下，边缘滚刀受力的峰值平均值约为其平均值的2～3倍，这与李辉等[13]的研究结果是一致的。

(a) 垂直力

(b) 滚动力

(c) 扭矩

图8边缘滚刀垂直力、滚动力和扭矩与时间的关系曲线(r=800 mm，θ=60°)

Fig. 8Vertical stresses, rolling stresses and torques of gage disc cutter vs. time (r=800 mm，θ=60°)

在一定过渡圆弧半径下，安装倾角θ=15°时边缘滚刀受力最小，安装倾角θ=60°时边缘滚刀受力最大。垂直力、滚动力和扭矩的平均值及峰值平均值都随着边缘滚刀安装倾角的增大而呈现近似线性的增长。

3.2.2边缘滚刀受力与刀盘过度段圆弧半径的关系

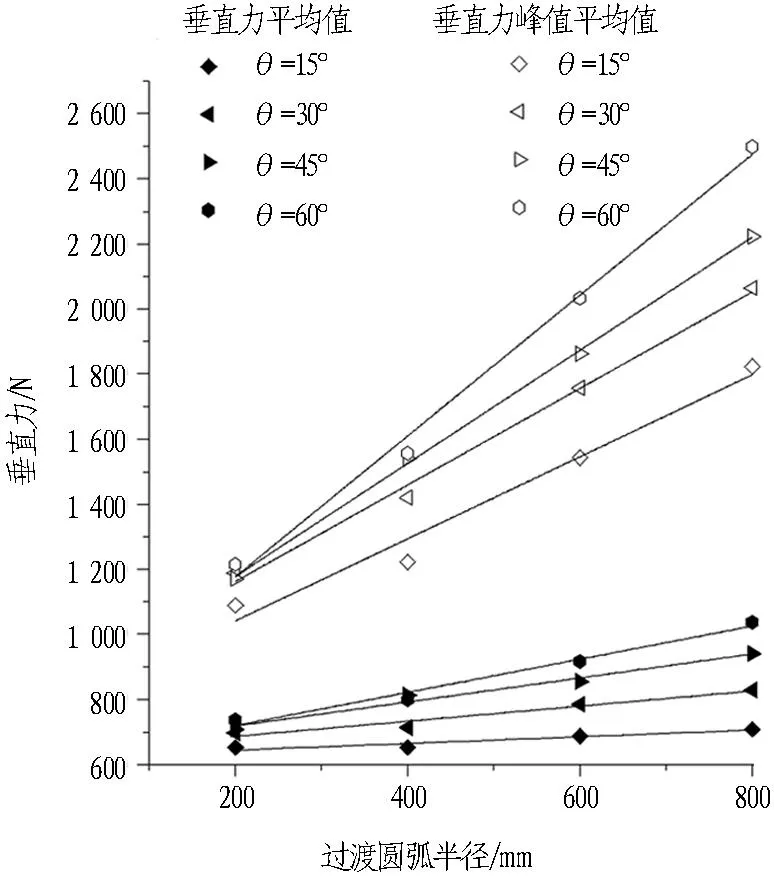
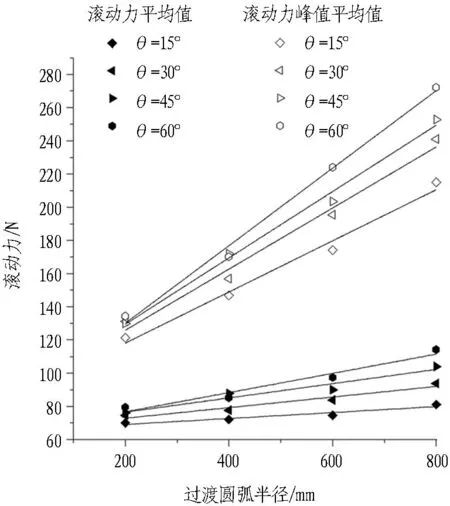
图10为边缘滚刀在不同刀盘过渡圆弧半径下的垂直力、滚动力和扭矩的变化情况。在一定安装倾角的情况下，过渡圆弧半径r=200 mm时边缘滚刀受力最小，r=800 mm时边缘滚刀受力最大。垂直力、滚动力和扭矩的平均值及峰值平均值都随着刀盘过渡圆弧半径的增大而呈现近似线性的增长。

(a) 垂直力

(b) 滚动力

(c) 扭矩

Fig. 9Vertical stresses, rolling stresses and torques of gage disc cutter under different installation angles

(a) 垂直力

(b) 滚动力

(c) 扭矩

Fig. 10Vertical stresses, rolling stresses and torques of gage disc cutter under different transition arch radii

3.3综合考虑安装倾角及过渡圆弧半径下的边缘滚刀受力分析

从图9可以看出，不同过渡圆弧半径时的边缘滚刀受力随倾角的变化是不同的。r=800 mm时边缘滚刀受力随倾角增长的速率大于r=200 mm时。过渡圆弧半径越大，滚刀受力回归直线的斜率越大，边缘滚刀受力随安装倾角的增长越迅速。从图10可以看出，不同安装倾角时的边缘滚刀受力与过渡圆弧半径的关系也是不同的。θ=60°时滚刀受力随倾角增长的速率要大于θ=15°时。边缘滚刀安装倾角越大，滚刀受力回归直线的斜率越大，边缘滚刀受力随过渡圆弧半径的增长越迅速。在分析边缘滚刀的受力情况时，除了应分析单因素作用下的边缘滚刀受力规律之外，还应将安装倾角和过渡圆弧半径2种因素结合在一起综合考虑。采用多元线性回归分析可得：

(5)

(6)

(7)

(8)

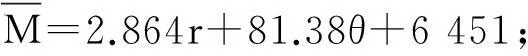
(9)

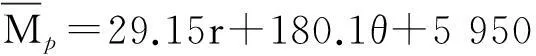
(10)

4结论与讨论

1)岩石具有一定的弹脆性，在边缘滚刀切削岩石过程中，会出现阶跃破碎的特点，滚刀受力曲线表现为高频率振荡，不断出现陡增和回落。

2)安装倾角和刀盘过渡圆弧半径是影响边缘滚刀受力的重要因素。边缘滚刀受力平均值及峰值平均值都随着安装倾角和刀盘过渡圆弧半径的增加而呈现近似线性的增长。

3)边缘滚刀的受力情况将直接影响边缘滚刀的使用寿命。目前关于边缘滚刀的布置参数对其受力情况影响的研究较少，这方面有待继续深入研究。

参考文献(References)：

[1]夏毅敏, 林赉贶, 罗德志, 等. 复合式土压平衡盾构盘形滚刀布置规律[J]. 中南大学学报(自然科学版), 2013,44(9): 3652-3657.(XIAYimin,LINLaikuang,LUODezhi,etal.DisccutterlayoutlawforcompositeEPBshield[J].JournalofCentralSouthUniversity(ScienceandTechnology), 2013,44(9): 3652-3657.(inChinese))

[2]沈斌.TBM边缘滚刀组合优化布置研究[D]. 长沙： 中南大学, 2014.(SHENBin.ResearchonoptimallayoutofTBMgagedisccutterscombination[D].Changsha:CentralSouthUniversity, 2014. (inChinese))

[3]宋克志, 李传明, 袁大军, 等. 盾构隧道施工盘形滚刀推力分布规律研究[J]. 岩石力学与工程学报, 2008,27(增刊2): 3875-3881. (SONGKezhi,LIChuanming,YUANDajun,etal.Studyondistributionregularitiesofdisccutterthrustforceforshieldtunneling[J].ChineseJournalofRockMechanicsandEngineering, 2008,27(S2): 3875-3881. (inChinese))

[4]张厚美.TBM的掘进性能数值仿真研究[J]. 隧道建设, 2006, 26(增刊2): 1-7. (ZHANGHoumei.Studyonnumericalsimulationsofperformanceoftunnelboringmachines(TBM)[J].TunnelConstruction, 2006, 26(S2): 1-7.(inChinese))

[5]吴元, 夏毅敏, 郭金成, 等.TBM边缘滚刀关键参数对破岩效率影响规律研究[J]. 现代隧道技术, 2015, 52(1): 119-126.(WUYuan,XIAYimim,GUOJincheng,etal.InfluenceofkeyparametersofaTBMgagedisccutteronrock-breakingefficiency[J].ModernTunnellingTechnology, 2015, 52(1): 119-126.(inChinese))

[6]王旭, 赵羽, 张宝刚, 等.TBM滚刀刀圈磨损机理研究[J]. 现代隧道技术, 2010, 47(5): 15-19.(WANGXu,ZHAOYu,ZHANGBaogang,etal.ResearchontheringwearmechanismofTBMdisccutter[J].ModernTunnellingTechnology, 2010, 47(5): 15-19. (inChinese))

[7]杨宏欣. 浅谈隧道施工中TBM滚刀失效及刀具管理[J]. 建筑机械化, 2008, 28(12): 60-62.(YANGHongxin.BrieflytalkingaboutTBMcuttermanagementinconstructingtunnel[J].ConstructionMechanization, 2008, 28(12): 60-62. (inChinese))

[8]高玮．岩石力学[M]. 北京: 北京大学出版社，2010: 27-30.(GAOWei.Rockmechanics[M].Beijing:PekingUniversityPress, 2010: 27-30.(inChinese))

[9]朱震寰.TBM盘形滚刀磨损演变数值模拟研究[D]. 长沙： 中南大学, 2013.(ZHUZhenhuan.Numericalsimulationofdisccutter’swearevolutionforTBM[D].Changsha:CentralSouthUniversity, 2013. (inChinese))

[10]郑聪, 赵威, 张海丰, 等. 不同贯入度下盘形滚刀受力数值研究[J]. 矿山机械, 2015,43(8): 118-123.(ZHENG Cong, ZHAO Wei, ZHANG Haifeng, et al. Numerical analysis of stress acting on disc cutter at various penetration depths[J]. Mining & Processing Equipment, 2015,43(8): 118-123.(in Chinese))

[11]宋克志, 袁大军, 王梦恕. 隧道掘进机 (TBM) 刀盘转速的讨论[J]. 建筑机械, 2005(8): 63-65.(SONG Kezhi, YUAN Dajun, WANG Mengshu. Discussion on cutterhead rotation speed of tunnel boring machine (TBM)[J]. Construction Machinery, 2005(8): 63-65.(in Chinese))

[12]纪昌明, 张照煌, 叶定海. 盘形滚刀刀间距对岩石跃进破碎参数的影响[J]. 应用基础与工程科学学报, 2008, 16(2): 255-263.(JI Changming, ZHANG Zhaohuang, YE Dinghai. The influence of the disk cutter space on rock’s jump break coefficients[J]. Journal of Basic Science and Engineering, 2008, 16(2): 255-263.(in Chinese))

[13]李辉, 王树林, 汪加科. TBM 盘形滚刀受力分析[J]. 现代隧道技术, 2012, 49(3): 193-197.(LI Hui, WANG Shulin, WANG Jiake. Force analysis of the disc cutter on a TBM[J]. Modern Tunnelling Technology, 2012, 49(3): 193-197.(in Chinese))

Influence of Layout Parameters on Stress of TBM Gage Disc Cutter

ZHENG Cong1， ZHAO Wei2， ZHANG Haifeng1， MA Baosong1

(1.FacultyofEngineering,ChinaUniversityofGeosciences(Wuhan),Wuhan430074,Hubei,China;2.CCCCSecondHighwayConsultantCo.,Ltd.,Wuhan430056,Hubei,China)

Abstract:Gage disc cutters installed on the edge of cutterhead of full-face tunnel boring machine (TBM) are subjected to complexity of stress due to the bad working conditions. Nonlinear dynamic models are established by using ABAQUS software so as to study the influence of layout parameters on stress of gage disc cutter; and the stress on the TBM gage disc cutter is analyzed. The results show that: 1) The stress on the gage disc cutter during rock breaking varies violently. 2) The installation angle and transition arc radius have a significantly influence on the stress of gage disc cutter. 3) The stress on the gage disc cutter increases approximately linearly with the installation angle and transition arc radius increase.

Keywords:TBM; gage disc cutter; installation angle; transition arc radius; finite elements

中图分类号：U 455.3

文献标志码：A

文章编号：1672-741X(2016)03-0349-06

DOI:10.3973/j.issn.1672-741X.2016.03.017

作者简介：第一 郑聪(1993—)，男，湖北荆州人，中国地质大学(武汉)地质工程专业在读硕士，主要研究方向为地质工程。E-mail: zhengcongcug@163.com。

收稿日期：2015-09-14; 修回日期： 2015-11-08