基于信号极化三维平稳性的飞行器姿态估计

黄海行，陈广东，陈　智

(南京航空航天大学 无人驾驶飞机研究院，江苏 南京 10016)



基于信号极化三维平稳性的飞行器姿态估计

黄海行，陈广东，陈智

(南京航空航天大学 无人驾驶飞机研究院，江苏 南京 10016)

摘要以电磁波为参照的飞行器姿态测量研究，可弥补空间参照物缺乏，丰富姿态测量手段。利用3个正交电(磁)场传感器接收电磁波三维电(磁)信号，测量运动平台姿态。该方法根据姿态参数估计的CRB(克拉美—罗界)是否为有限值，判断该环境电磁波信号能否用于运动平台姿态测量；根据基准姿态与实时姿态互相关矩阵变化，估计得到实时天线坐标系到基准天线坐标系的转换矩阵，据此将实时姿态坐标系下的运动平台姿态，转换到基准姿态坐标系下，再转换到地理坐标系下，完成运动平台姿态感知。电磁波信号可以为独立或相干信号，波达方向和极化状态任意，可不受多径效应困扰。仿真试验表明该方法稳定有效。

关键词电磁矢量传感器；极化状态；波达方向；姿态导航

Aircraft Attitude/Heading Estimation Based on 3D Statistical Characteristics of Polarization Electric (Magnetic) Stable Signal

HUANG Hai-xing,CHEN Guang-dong,CHEN Zhi

(ResearchInstituteofUnmannedAircraft,NanjingUniversityofAeronautics&Astronautics,NanjingJiangsu210016,China)

AbstractThe attitude measurement based on electromagnetic wave can make up for the lack of spatial reference,and enrich the method of attitude measurement.In this paper,moving platform attitude is measured from the electromagnetic waves received by the three orthogonal dipole electric (magnetic) antennas.The CRB (Cramer Rao Bound) of the parameters estimation will determine whether the environmental electromagnetic wave signal can be used to measure moving platform Attitude/Heading.The transformation matrix,from the real-time antenna coordinates to the reference antenna coordinates,is obtained by comparing their correlation matrixes.We convert the platform attitude of the real-time antenna coordinates,into the reference antenna coordinates,then into the geographical coordinates.And the platform attitude is percept.The electromagnetic wave signals can be independent or coherent signal,and the attitude/heading estimation is not affected by multipath effect.Simulation experiment shows that the method is stable and effective.

Key wordsEM Vector Sensor;state of polarization;DOA(wave direction of arrival);attitude determination

0引言

人造的和自然界的各种电磁波充斥着地球表面和太空，这些电磁波信息与接收平台姿态具有密切关联性，电磁波提供的姿态基准不受运动平台姿态及其运动影响，可以像利用地磁场指南那样利用电磁波测量运动平台姿态。国内外都研究在地球卫星导航系统接收端，利用多点接收、三角计算的方法感知姿态[1-9]，缺点是体积大、精度低、系统复杂和速度慢，影响了该技术的推广应用。本文利用3个正交电(磁)场传感器接收电磁波三维电(磁)信号测量运动平台姿态，可以单点测量飞行器姿态,接收信号既可以相互独立，也可以相干，信号数任意，波达方向和极化状态任意，各信号强弱任意，因此不受多径效应困扰，既可以利用主动发射电磁波信号，也可以被动接收空间分布的广播电磁波信号测量姿态，提高了系统的隐蔽性,进一步揭示了电磁波测量姿态的能力。

1信号模型

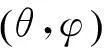
图1　极化电磁波椭圆状旋转电场波结构

电磁矢量传感器接收单元示意图如图2所示。全电磁矢量传感器包含3个正交电场和3个正交磁场接收单元。

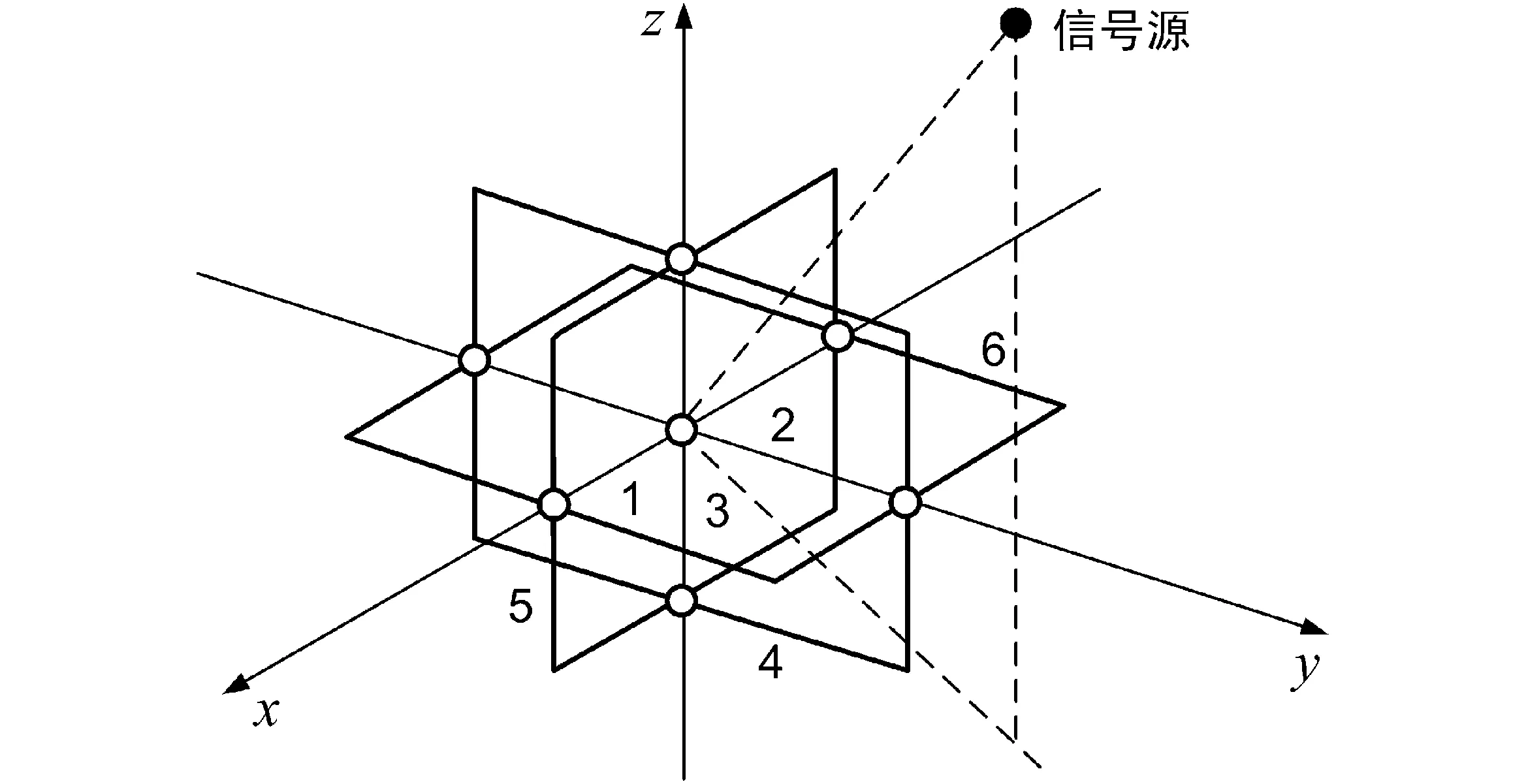
图2　电磁矢量传感器接收单元示意

3个正交电场传感器为3正交偶极子天线，在基准姿态从第n信号源接收到的信号导向矢量表达为[10]：

式(1)信号导向矢量可进一步表示为：

an=BnDn。

(2)

式中，Bn为波结构坐标系(见图1) 到平台天线坐标系的转换矩阵，

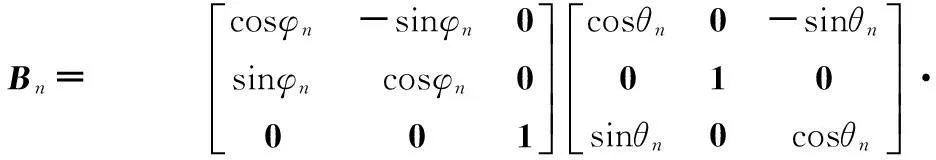
Bn= cosφn-sinφn0sinφncosφn0001éëêêêùûúúúcosθn0-sinθn010sinθn0cosθnéëêêêùûúúú·

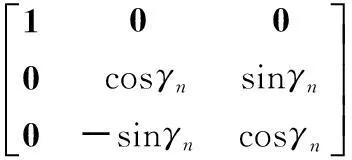
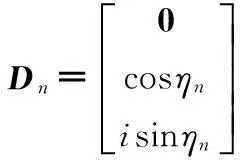
2姿态测量基本原理

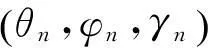
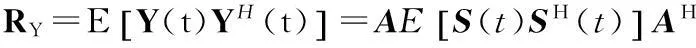
平稳的固定信号源的RY为常数阵。

当运动平台姿态变化，天线的接收信号不同于基准姿态信号，实时姿态时接收信号为：Y′(t′)=μA′S(t′)+e′(t′)，其中，Y′(t)=[y1′(t′),y2′(t′),y3′(t′)]T，A′=[a1′,…,an′]为3×N矩阵，e′(t′)为随机噪声，μ为接收机因姿态变化形成的信号复衰减因子。3个正交电场传感器从第n信号源接收到的信号导向矢量表达为：

an′=Bn′ Dn。

其中波结构坐标系到实时天线坐标系的转换矩阵

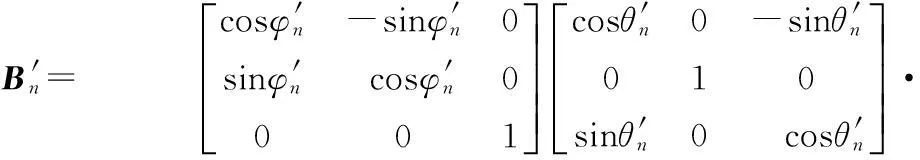
Bn'= cosφn'-sinφn'0sinφn'cosφn'0001éëêêêùûúúúcosθn'0-sinθn'010sinθn'0 cosθn'éëêêêùûúúú·

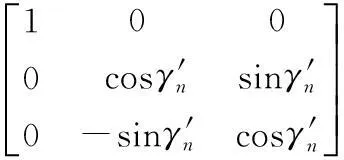
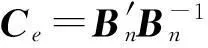
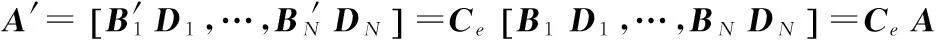
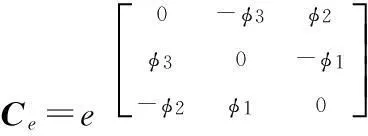
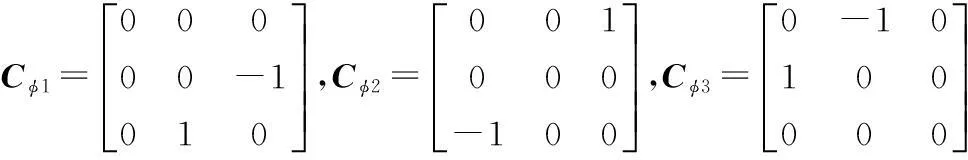
实时姿态时接收信号互相关矩阵为：

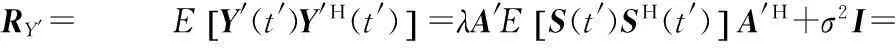
RY'= EY'(t')Y'H(t')[]=λA'ES(t')SH(t')[]A'H+σ2I=

式中，λ=μμH为衰减因子。

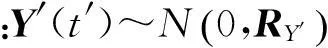
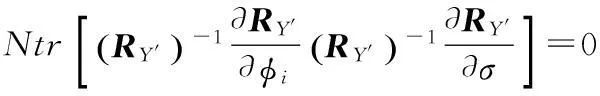
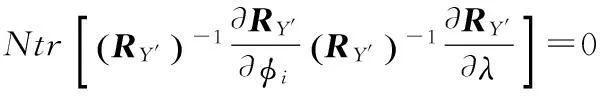
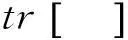
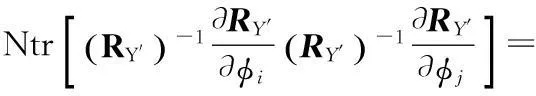
(3)

3参数估计算法

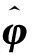
可得，

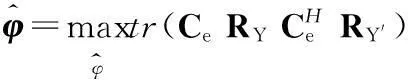
式中，符号vec()表示将矩阵各列组合为向量。

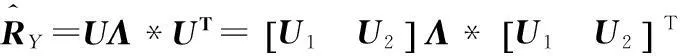
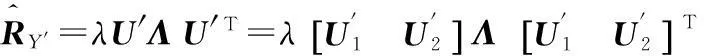
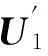
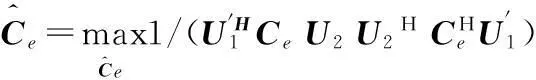
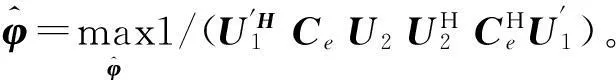
接收信号可以为相干信号，不受多径效应困扰，信号总数N可以为1到无穷大，波达方向和极化状态任意，各信号强弱任意。对接收电磁波环境的要求是式(3)确定的CRB为有限值；接收极化三维电(磁)信号互相关矩阵在解除接收姿态旋转变化影响后保持平稳，即运动平台测量姿态所处时、空、频、极化域，信号二次统计特性不变。因此本文既可以主动利用发射电磁波信号，也可以被动利用空间分布的广播电磁波信号测量姿态，提高了系统的隐蔽性。

4姿态测量具体实施步骤

姿态测量具体实施步骤如下：

① 确定运动平台基准姿态坐标系与大地坐标系转换关系。

② 在运动平台基准姿态以极化敏感的电磁矢量传感器中的3个正交电(磁)场传感器接收电磁波信号，估计三维电(磁)信号互相关矩阵。计算姿态参数估计的CRB(克拉美—罗界)是否为有限值,判断该环境电磁波信号能否用于运动平台姿态测量。

该步骤对电(磁)极化三维特征进行学习评估，在单一接收点以极化敏感的电磁矢量传感器中的3个正交电(磁)场传感器在基准姿态接收电磁波信号，选取时间t中的K个采样点采样k=1,2,…,K次，计算估计值为：

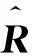
③ 在运动平台实时姿态以极化敏感的电磁矢量传感器中的3个正交电(磁)场传感器接收电磁波信号，计算估计三维电(磁)信号互相关矩阵。对实时姿态和基准姿态互相关矩阵RY′和RY，进行特征植分解，根据各自特征值比例是否近似相等，初略判断该环境电磁波信号是否平稳。

⑤ 用步骤④得到转换矩阵将实时姿态坐标系下的运动平台姿态，转换到基准姿态坐标系下，再转换到地理坐标系下，完成运动平台姿态感知。

在接收机平台实时姿态坐标系中，平台姿态方向向量为单位阵

根据电磁信号对称性，可单独利用电或磁信息测量运动平台姿态,也可融合电磁信息提高测量姿态精度。

5仿真实验

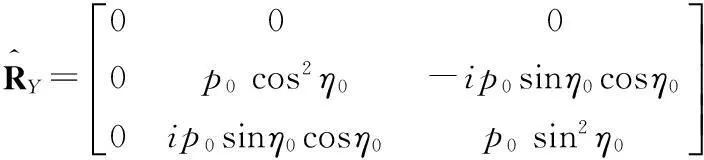
式中，p=λp0。

代入式(3)得：

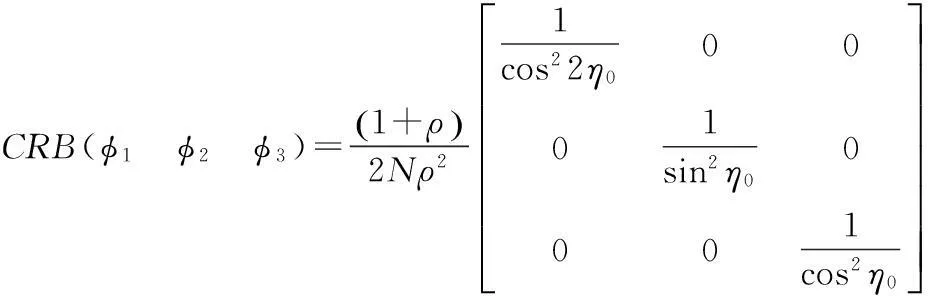
式中，ρ=p/σ2，这个结果与文献[10]一致。由此式知，η0=±45°的圆极化随机信号的CRB(φ1)=，不能用于测量姿态。

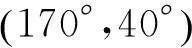
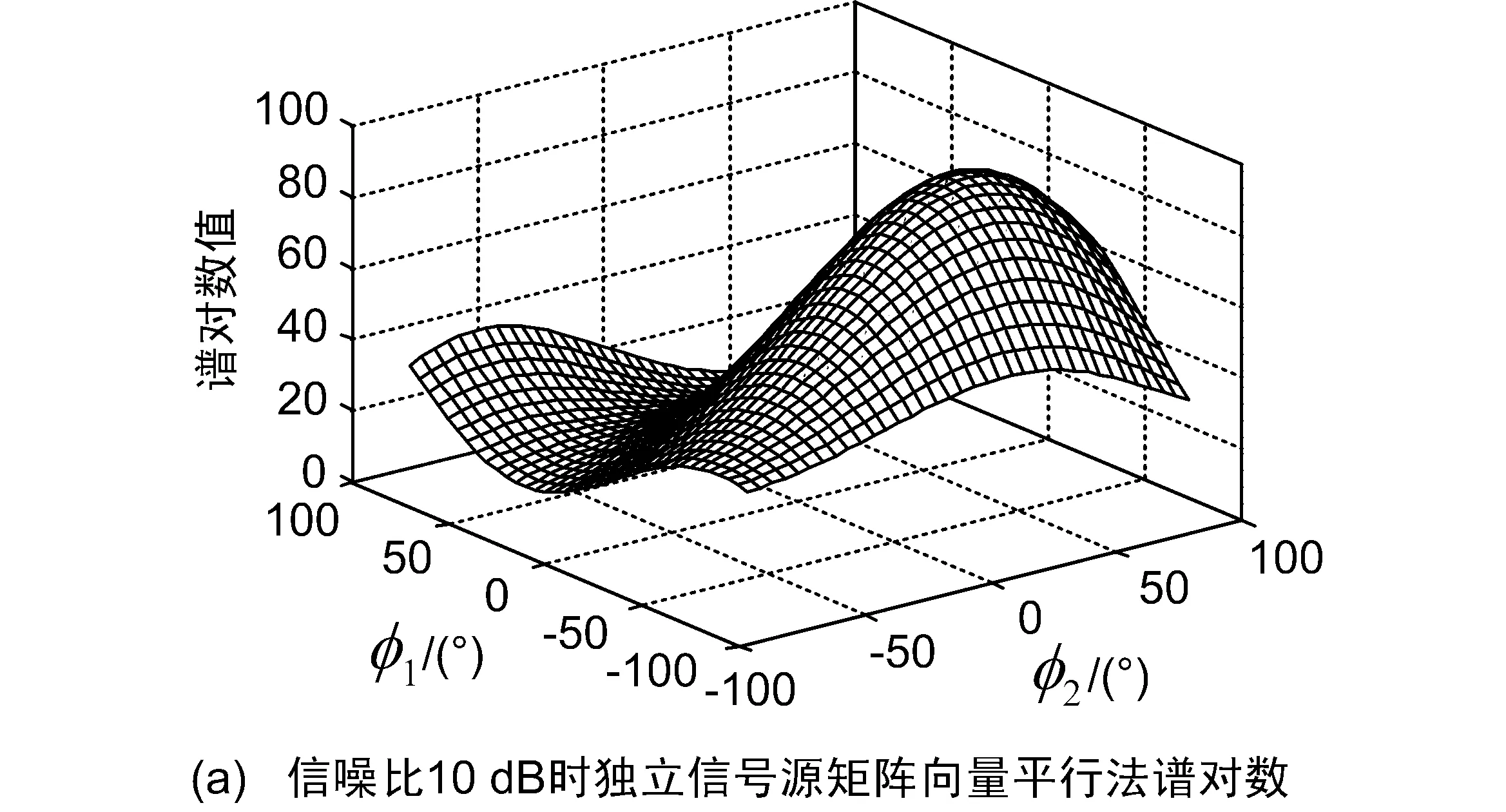
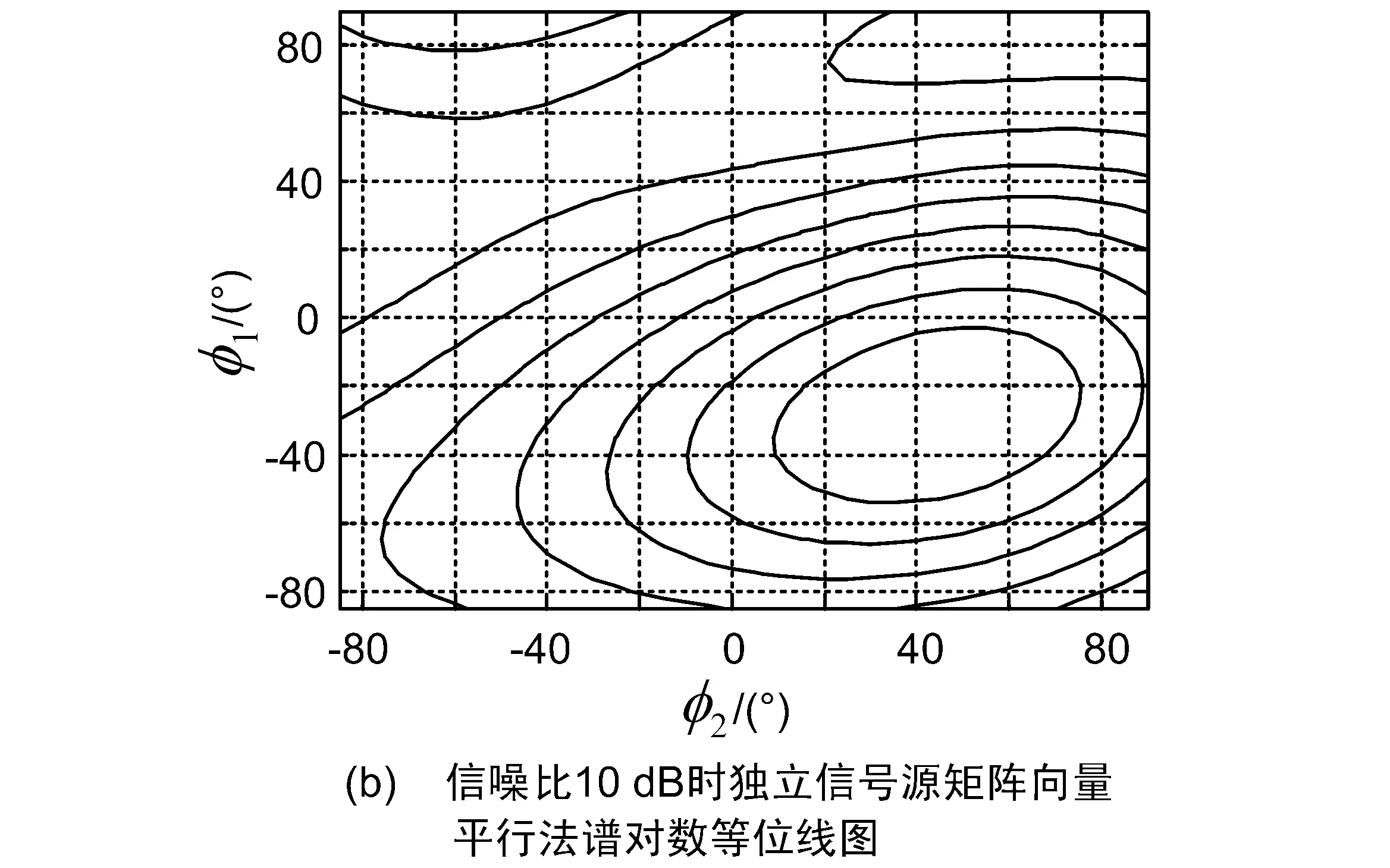
图3　矩阵向量平行法谱对数随φ1和φ2变化图形

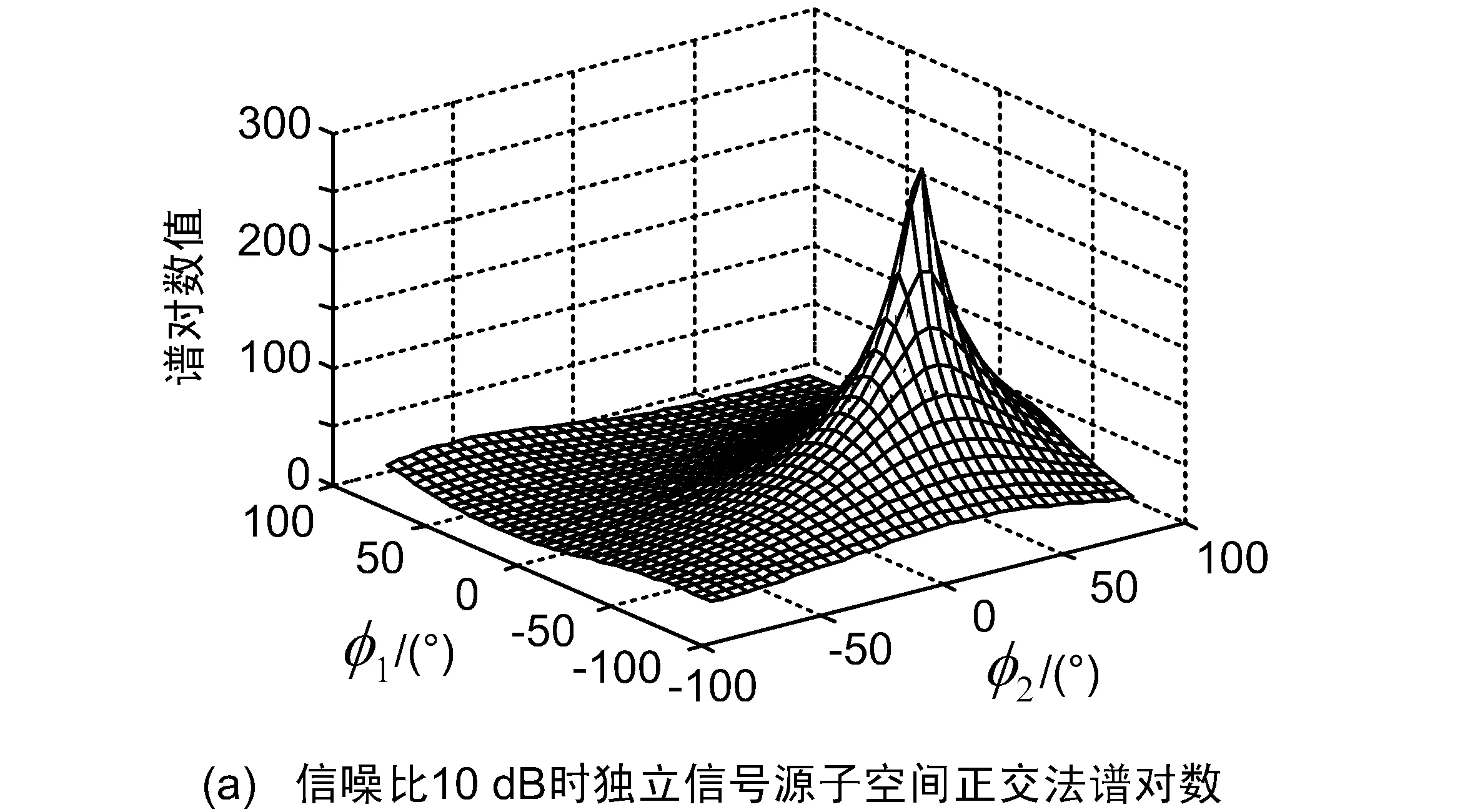
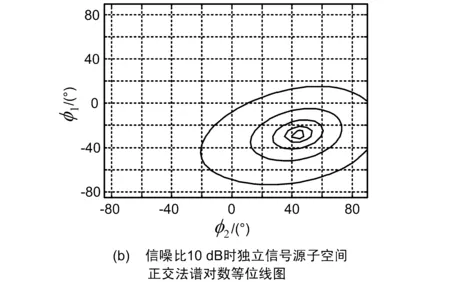
图4　子空间正交法谱对数随φ1和φ2变化图形

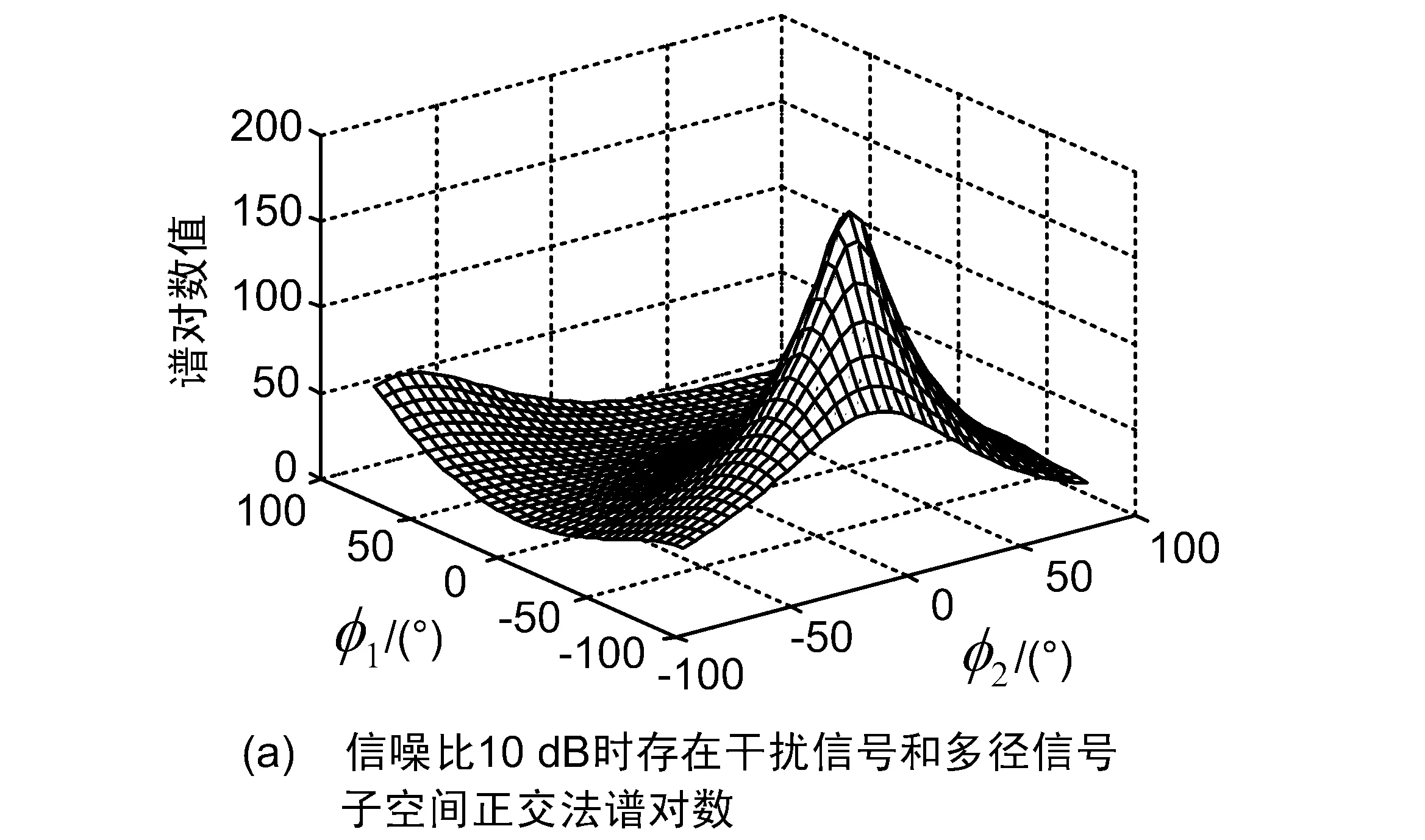
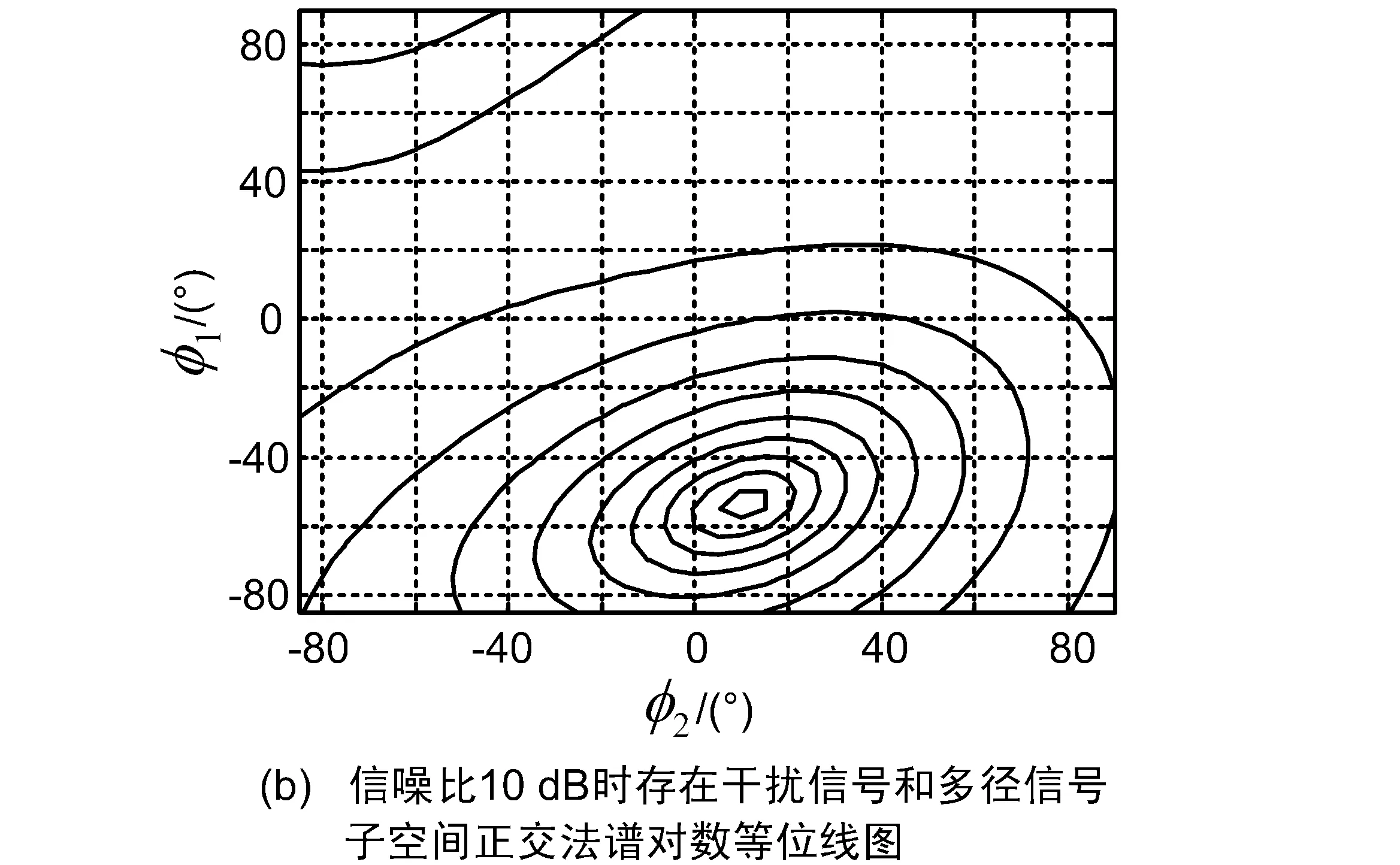
图5　未校正基准互相关矩阵子空间正交法谱对数随φ1和φ2变化图形

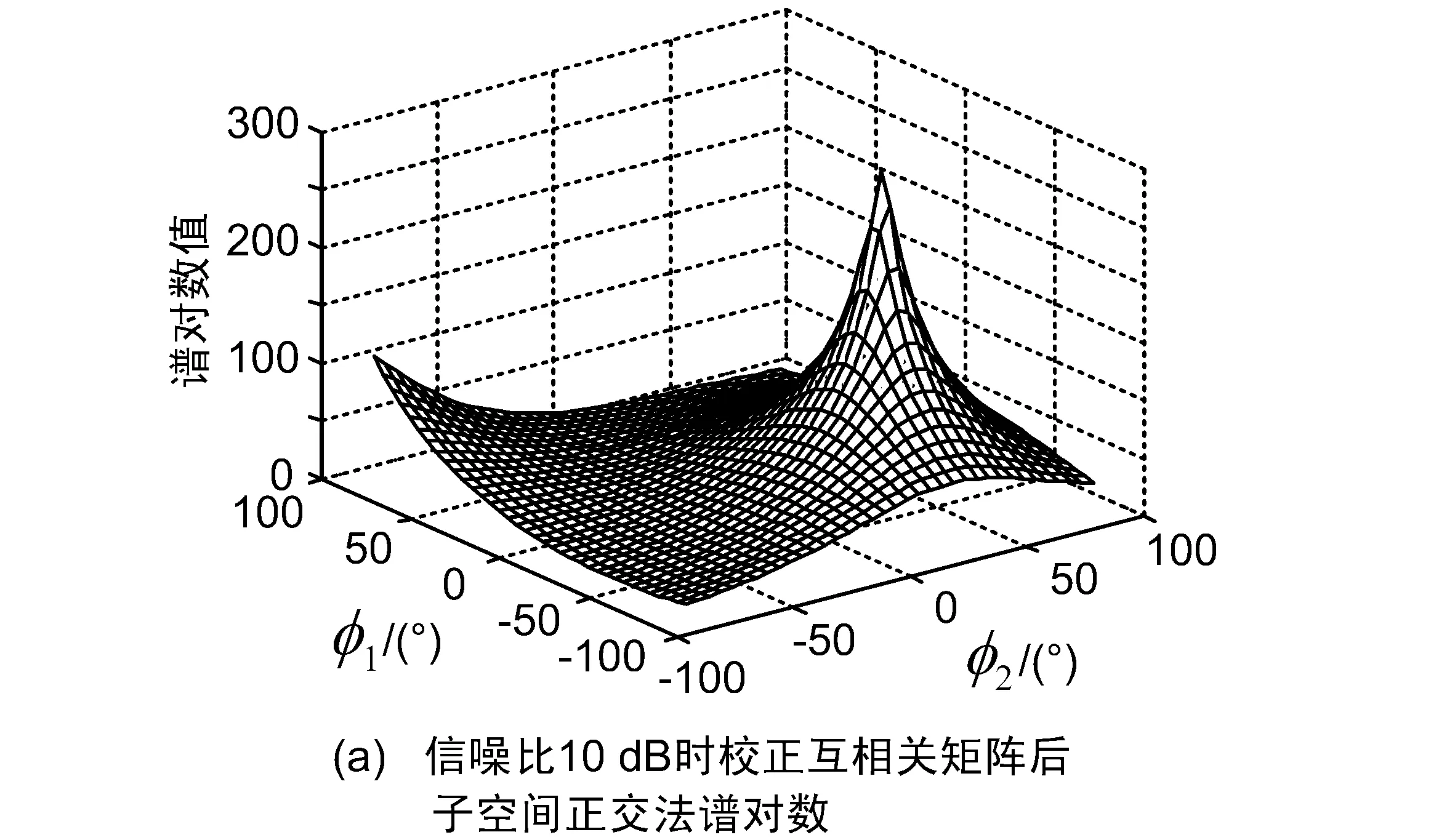
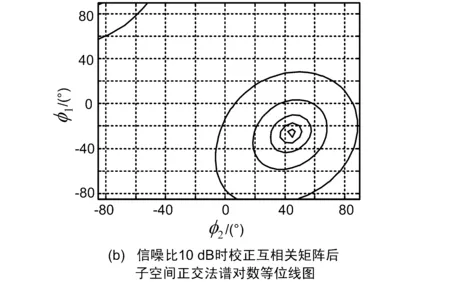
图6　校正基准互相关矩阵后子空间正交法谱对数随φ1和φ2变化图形

6结束语

测控技术利用电磁波时域信息测距，频域信息测速,空域信息测方位,极化域信息却没有得到深入研究和利用,本文正是在这一领域展开探索,只需运动平台上有单一接收点，就可实现姿态/航向感知，系统可微型化，信号不受多径效应困扰，既可以利用主动发射电磁波信号，也可以被动接收空间分布的广播电磁波信号测量姿态，提高了系统的隐蔽性。适用于空或天飞行器。

参考文献

[1]CHAO A,KANG Y S.Altitude Integration of Radar Altimeter and GPS/INS for Automatic Takeoff and Landing of a UAV[C]∥KINTEX,Gyeonggi-do,Korea .11th International Conference on Control,Automation and Systems,2011:1 429-1 432.

[2] HAN S L,WANG J L.Quantization and Colored Noises Error Modeling for Inertial Sensors for GPS/INS Integration[J].IEEE SENSORS JOURNAL,2011,11(6):1 493-1 503.

[3]WANG X l,SHAOX W,GONG D R,et al.GPS/VISNAV Integrated Relative Navigation and Attitude Determination System for Ultra-close Spacecraft Formation Flying[J].Systems Engineering and Electronics,2011,22(2):283-291.

[4]GABRIELE G,PETER J G,TIM P G. Instantaneous Global Navigation Satellite System (GNSS)-Based.Attitude Determination for Maritime Applications[J].Oceanic Engineering,IEEE,2012,12(99):1-15.

[5]KIS L,LANTOS B.Aided Carrier Phase Differential GPS for Attitude Determination[C]∥ASME,IEEE International Conference on Advanced Intelligent Mechatronics (AIM),2011:778-783.

[6]ANDREW R,ABDELHAMID T.On the Attitude Estimation of Accelerating Rigid-bodies Using GPS and IMU Measurements[C]∥Orlando,FL,USA,2011 50th IEEE Conference on Decision and Control,European Control Conference (CDC-ECC),2011:8 088-8 093.

[7]吴美平,逯亮清.北斗双星系统车辆定向技术[J].国防科技大学学报,2006,28(3):89-93.

[8]AXELRAD P,WARD L M.Spacecraft Attitude Estimation Using the Global Positioning System：Methodology and Result for RADCAL[J].Journal of Guidance,and Dynamics，1996,19(6):1 201-1 209.

[9]NAQVI N A,Li Y J.The Quest for Optimal Spacecraft Attitude Determination Filtering Algorithm Using GNSS Phase Measurements:An Overview[C] ∥Japan,2nd International Conference on Signal Processing Systems (ICSPS),2010,V2:383-388.

[10]NEHORAI A,PALDI E.Vector-sensor Array Processing for Electromagnetic Source Location[J].IEEE Transactions on Signal Processing,1994(42):376-398.

[11] SHUSTER M.Survey of Attitude Representations[M].United States,Hopkins Univ Applied Physics Lab,1993:439-517.

[12]MARIUS P,ALEX B G.Maximum-likelihood Direction-of-Arrival Estimation in the Presence of Unknown Nonuniform Noise[J].IEEE Transactions on Signal Processing,2001,49(7):1 310-1 324.

[13]HOCHWALD B,NEHORAI A.Concentrated CramCr-Rao Bound Expressions[C]∥IEEE Trans.Inform.Theory,1994:125-142.

[14] STOICA P,NEHORAI A.Performance Study of Conditional and Unconditional Direction-of-Arrival Estimation[J].IEEE Trans.Acoust.Speech Signal Processing,1990,38(10):1 783-1 795.

[15] 陈广东,李成珠.基于极化电磁波信息链的运动平台感知方法[P].中国专利：201110093296.2,2011.

[16] 陈广东.基于协同源波达信息的运动平台姿态感知方法[P].中国专利： 201210483494.4，2013.

黄海行男，(1991—)，硕士研究生。主要研究方向：测控信号处理。

陈广东男，(1968—),博士，研究生导师，副研究员。主要研究方向：测控、雷达成像。

作者简介

中图分类号TN911

文献标志码A

文章编号1003-3106(2016)04-0030-05

收稿日期：2016-01-07

doi:10.3969/j.issn.1003-3106.2016.04.08

引用格式：黄海行,陈广东,陈智.基于信号极化三维平稳性的飞行器姿态估计[J].无线电工程,2016,46(4):30-34，51.