一种部分响应CPM信号的调制参数盲估计算法

靳晓艳，李　伟

(1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；

2.空军驻石家庄地区军代室，河北 石家庄 050081)



一种部分响应CPM信号的调制参数盲估计算法

靳晓艳1，李伟2

(1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；

2.空军驻石家庄地区军代室，河北 石家庄 050081)

摘要针对非协作通信环境下部分响应CPM信号的调制参数盲估计问题，提出了一种系统的参数估计方案，可依次对载波频率、符号速率、调制指数和调制阶数进行有效地估计。在基于循环平稳特性的符号速率估计的前提下，对联合估计算法进行简化，构造新的代价函数，实现载波频率和调制指数联合估计，提取循环谱线特征估计调制阶数。仿真试验表明，该算法在信噪比10 dB时具有较好的估计效果。

关键词CPM；调制参数；盲识别；循环谱

A Blind Modulation Parameter Estimation Algorithm for Partial Responses CPM Signal

JIN Xiao-yan1,LI Wei2

(1.The54thResearchInstituteofCETC,ShijiazhuangHebei050081,China；2.MilitaryRepresentativeOfficeofPLAAirForceStationedinShijiazhuangRegion，ShijiazhuangHebei050081,China)

AbstractA systematic scheme is proposed to solve the problem of modulation parameter estimation for partial responses CPM signal in non-cooperative communication environment.It can successively estimate carrier frequency,symbol rate,and modulation index and modulation order.After the estimation of symbol rate based on the features of cyclostationary of CPM signals,the joint estimation algorithm is simplified and a new cost function is constructed to estimate frequency offset and modulation index jointly.Lastly the modulation order is estimated by picking up features of cyclic spectrum line.Simulation results indicate that the algorithm can provide great performance under the SNR of 10 dB.

Key wordsCPM;modulation parameter;blind recognition;cyclic spectrum

0引言

连续相位调制(CPM)是一种相位连续、包络恒定的调制方式[1]，具有很高的频谱利用率和功率利用率，在现代移动通信和卫星通信系统中获得了广泛的应用，目前许多战术跳频电台也采用了这种调制样式[2]。因此，近几年通信侦察中颇为重视针对这种调制方式的信号盲检测和参数的分析识别技术。

在CPM调制参数盲估计方面，文献[3-7]中使用一些传统的基于信号循环平稳特性的方法可以实现全响应CPM信号参数盲估计，但对于部分响应CPM信号，过宽的信号过渡带宽会导致这些算法失效。文献[8-9]中使用高阶累积量对调制指数进行盲估计，但该算法也同样只适用于全响应CPM信号。本文提出了一种CPM信号的调制参数盲估计方法，能够适用于包括部分响应信号在内的全部类型CPM信号，并通过仿真试验验证了算法的有效性。

1CPM信号的数学模型

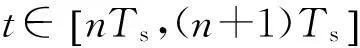
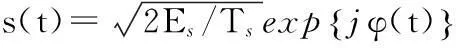
(1)

(2)

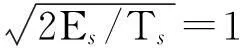
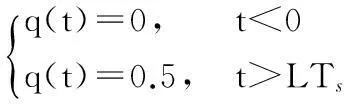
(3)

q(t)可以表示为频率成形脉冲g(t)的积分，

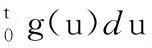
(4)

g(t)仅在区间(0,LTs]内具有非零值，LTs为频率成形脉冲的持续时间，正整数L称为频率成形脉冲相关长度，当L=1时，称为全响应CPM信号；当L>1时，称为部分响应CPM信号。

2CPM信号的参数估计

对CPM信号进行参数估计时，需要估计的参数有：载频fc、符号速率Rs、调制指数h和调制阶数M。文献[10]提出的调制指数/频偏/符号速率联合估计算法，需要的参数先验信息较少，并且具有很好的估计效果。然而该算法中符号周期搜索区间的确定非常困难，尤其对于部分响应CPM信号，带宽受成形波形长度的影响，于是用粗略估计的带宽来确定符号周期搜索区间往往导致联合估计错误。本文对该联合算法进行了改进，即先采用循环谱算法对符号速率进行精确估计，再利用简化后的联合算法进行调制指数和频偏的联合估计。因此，CPM信号参数估计方案如图1所示。

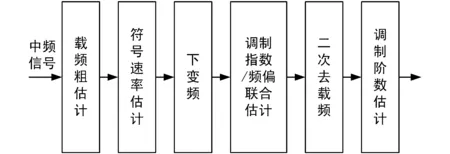
图1　CPM信号参数估计流程

2.1载频粗估计

(5)

2.2符号速率估计

CPM信号在谱频率为载频的循环截面上，有等间距的离散谱线，且其间距为信号的符号速率[11]。因此可以利用信号循环谱截面特征，直接对接收的中频信号进行符号速率估计。

因此，对接收到的CPM信号，用频域谱平滑法得到其循环谱估计，利用非线性滤波方法提取谱频率为载频的循环截面上的离散谱线，根据该截面上离散谱线的分布距离，得到符号速率的估计。

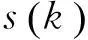
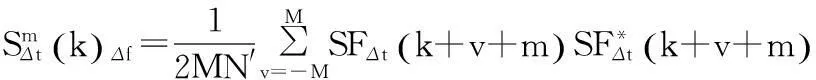
(6)

(7)

2.3调制指数和频偏联合估计

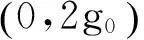
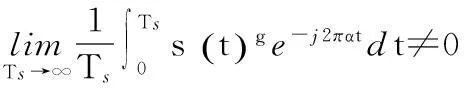
(8)

由于本参数估计方案中已经对符号速率进行了精确估计，因此可对文献[10]算法进行简化，定义代价函数为：

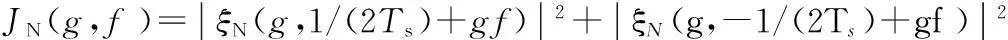
(9)

2.4调制阶数估计

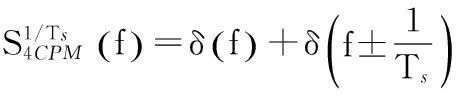
(10)

因此，四进制CPM信号的循环谱在f=0和f=±1/Ts处出现3根离散谱线。同理，八进制CPM信号的循环谱存在7根离散谱线。可见，对于调制指数h=1时不同调制阶数的CPM信号，在循环频率α=1/Ts处的循环谱具有不同的离散谱线特征，因此可以根据α=1/Ts处循环谱的谱线结构来对CPM信号的调制阶数进行识别。

对于h≠1的CPM信号，需要对h进行调整，使得调整后的调制指数h′满足h′=1。令μ=1/h，对CPM信号进行μ次方运算：

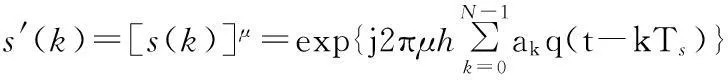
(11)

s′(k)即为调整后的CPM信号，对s(k)的μ次方运算仅仅改变其调制指数，对其他的调制参数没有影响，因此调整后的CPM信号也具有以上分析的循环平稳性。

3算法仿真与性能分析

通过仿真试验验证本文所提算法的有效性。假设四进制CPM信号的符号速率Rs=200 ksps；载波频率fc=400 kHz；采样率fs=2 MHz；观测码元长度N=1 024；成形脉冲为升余弦脉冲，成形波形长度L=2；调制指数h=2/5。

下面给出了使用本文算法对上述信号进行参数估计的结果。f=fc的循环谱截面如图2所示，根据离散谱线位置可正确估计符号速率；调制指数和频偏联合估计的代价函数分布图如图3所示，根据最高点位置可正确估计调制指数与频偏；α=1/Ts的循环谱截面如图4所示，根据谱线根数与位置可正确估计调制阶数。此外，该算法对于全响应CPM信号同样适用。

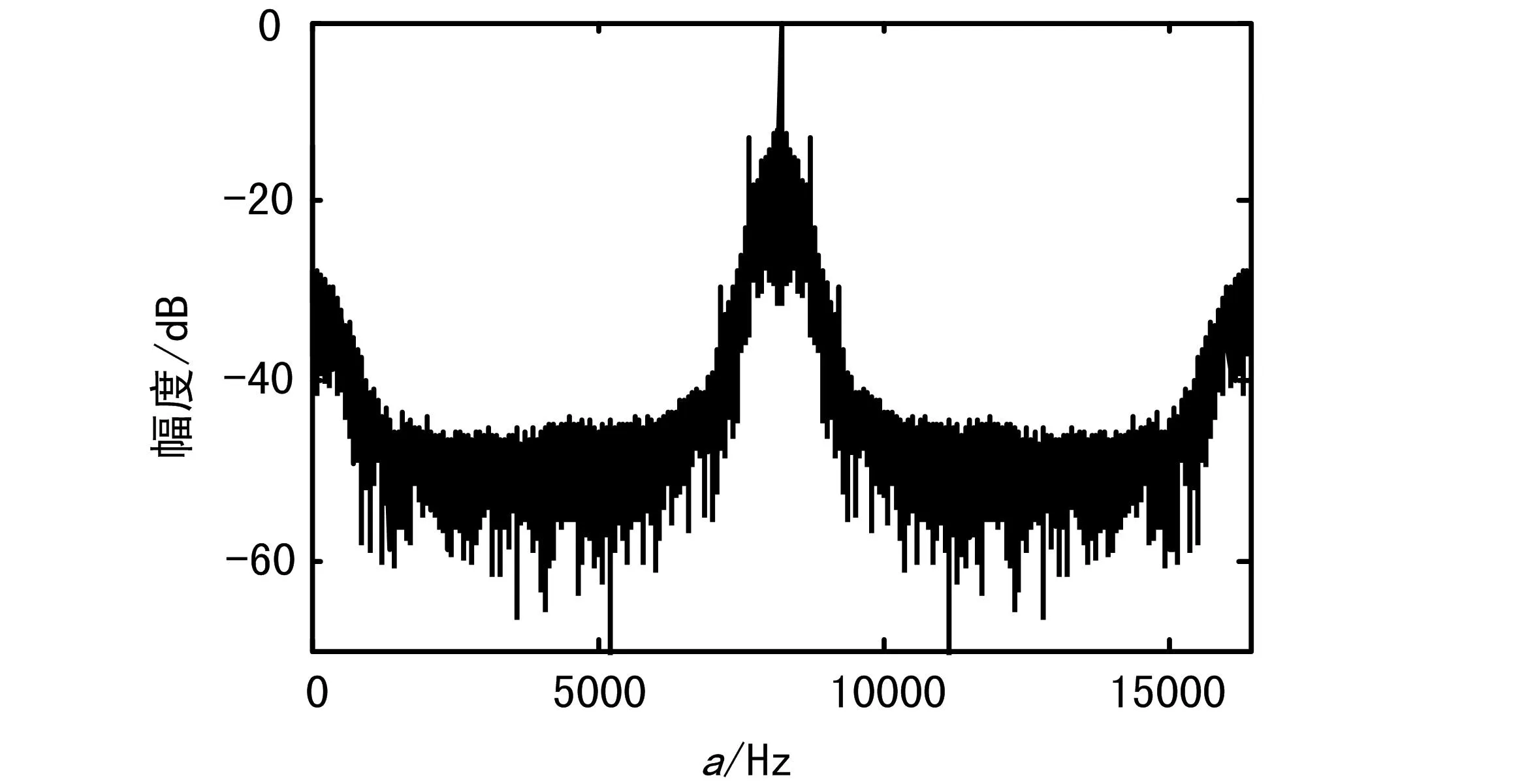
图2　f=fc的循环谱截面

图3　代价函数分布

随信噪比的变化，使用本文算法对上述仿真条件下的CPM信号进行100次蒙特卡罗试验的统计结果如表1所示。可以看出，当信噪比达到10 dB以上时，本算法能够有效估计符号速率、载频、调制指数和调制阶数。

表1　不同信噪比下CPM信号参数估计结果

4结束语

在非协作数字通信系统中要实现CPM信号的盲解调，接收端首先需要完成信号调制参数的盲估计。本文研究了部分响应CPM信号调制参数盲估计问题，提出了一种系统的参数估计方案，可以有效地对部分响应CPM信号的载波频率、符号速率、调制指数以及调制阶数进行估计，并通过仿真试验对本文所提算法进行了性能验证。

参考文献

[1]周家喜.非协作通信中连续相位调制信号盲解调关键技术研究[D]．合肥：中国科学技术大学，2009.

[2]周家喜，徐佩霞，戴旭初．一种基于循环平稳性的CPM信号调制阶数盲识别算法[J].信号处理，2010，26(4):578-580.

[3]杨书玲.一种CPM信号参数盲估计方法[J].无线电通信技术，2013，39(2):29-35.

[4]CIBLAT P,LOUBATON P,SERPEDIN E.et al.Asymptotic Analysis of Blind Cyclic Correlation Based Symbol Lrate Estimation[J].IEEE Transactions on Information Theory，2002，7(7):1 922-1 934.

[5]GARDNER W A.Statistical Spectral Analysis:A Nonprobabilistic Theory[M].Englewood Cliffs，NJ:Prentice-Hall，1988.

[6]吴厚明，吴量，江桦．一种基于循环平稳性的CPM信号符号速率盲估计算法[J]．信息工程学院学报，2012，13(2):224 -228.

[7]王宁，彭华，崔伟亮．一种非辅助数据的连续相位调制信号符号速率估计算法[J]．信号处理，2010，26(12):1 864-1 869.

[8]FONOLLOSA J R,FONOLLOSA J A R.Estimation of the Modulation Index of CPM Signals Using Higher Order Statistics[J].ICASSP,Minneapolis,1993(4):268-271.

[9]NIKIAS C L,FONOLLOSA J R.Analysis of CPM Signals Using Higher Order Statistics[J].MILCOM,1993(2):663-667.

[10]BIANCHI P,LOUBATON P,SIRVEN F.Nondata Aided Estimation of the Modulation Index of Continuous Phase Modulation[J].IEEE Transactions onSignal Processing.2004,52(10):2 847-2 861.

[11]NAPOLITANO A,SPOONER C.Cyclic Spectral Analysis of Continuous-phase Modulated Signal[J].IEEE Transactions on Signal Processing，2001,49(1):30-44.

[12]ZHANG Zi-bing,LI Li-ping,XIAO Xian-ci.The Characteristic Analysis of Second Order Cyclostationarity of Continuous Phase Modulation Signal[J].Journal of Electronics & Information Technology,2005,27(11):1 726-1 731.

[13]NAPOLITANO A,SPOONER C M.Cyclic Spectral Analysis of Continuous-Phase Modulated Signal[J].IEEE Trans.on SP,2001,49(1):30-44.

靳晓艳女,(1984—)，博士，工程师。主要研究方向：电子对抗。

李伟男,(1983—)，工程师。主要研究方向：信号与信息处理。

作者简介

中图分类号TN 911.7

文献标志码A

文章编号1003-3106(2016)04-0026-04

基金项目：国家部委基金资助项目。

收稿日期：2016-01-06

doi:10.3969/j.issn.1003-3106.2016.04.07

引用格式：靳晓艳，李伟.一种部分响应CPM信号的调制参数盲估计算法[J].无线电工程,2016,46(4):26-29.