对数据后处理雷达的多参数协同相关干扰*
柳 向,王杰贵,孟祥豪
(电子工程学院,合肥 230037)
对数据后处理雷达的多参数协同相关干扰*
柳向,王杰贵,孟祥豪
(电子工程学院,合肥230037)
摘要:基于DRFM转发或者重复转发的干扰信号,虽然在功率上能达到干扰要求,但是产生的虚假目标与真实目标缺乏相关性,数据后处理雷达能根据该特性实现对欺骗干扰信号的检测和抑制。针对数据后处理雷达在抑制非相关干扰信号的优越表现,根据不同特征域干扰信号的相关性要求,提出了在幅度域上具有起伏特性,时频域协同一致,方位上具有相关性的干扰信号模型,以保证对数据后处理雷达干扰的有效性。最后在与非相关干扰信号比较中,验证了该干扰方式的有效性。
关键词:时频域协同相关干扰,幅度控制,方位控制,数据后处理能力指标
0 引言
随着雷达技术的迅速发展,各种新体制雷达不断出现,为了提高单部雷达的抗干扰性能,出现了以马斯特(Master)雷达为代表的具有数据后处理抗干扰能力的雷达(以下简称数据后处理雷达)。数据后处理雷达通过对接收的雷达回波数据进行分析与后期处理,根据目标信号与欺骗干扰信号在幅度域、时域、频域、空域、极化域等一维或多维特征方面的差异,最大限度地抑制各种干扰能量,使最终进行目标检测和参数测量时的信噪比、信杂比达到最大[1]。
干扰技术随着雷达新体制和抗干扰技术的发展而发展,目前针对特定体制雷达的干扰主要包括:对相控阵雷达的干扰、对合成孔径雷达的干扰、对脉冲多普勒雷达的干扰以及对MIMO雷达的干扰等[2-5],而针对数据后处理雷达的干扰研究相对较少。文献[6]考虑了移频干扰带来的信号失配,提出了一种采用幅度调制补偿的相干移频干扰方法,但是该方法只考虑干扰信号的功率匹配,并没有考虑干扰信号的幅度起伏特性。文献[7]中为了破坏PD通过速度跟踪系统获得目标的方位和距离信息,对速度拖引干扰作了详细说明与效果评估,但是文中并没有考虑多普勒频移函数与时延函数的逻辑关系。文献[8]针对欺骗干扰产生的干扰数目单一,利用DRFM将截获的雷达信号存储、处理,按程序设定的转发间隔重复读出当前采样信号并转发,产生了多个距离-速度欺骗假目标,但是该方法并没有考虑干扰实施的方位信息。本文针对不同特征域干扰信号的相关性要求,提出了在幅度域上具有起伏特性,时频域协同一致,方位上具有相关性的干扰信号,保证了对数据后处理雷达干扰的有效性。
1对数据后处理雷达的相关干扰控制
数据后处理雷达根据处理域的不同,常见的后处理抗干扰方法主要有:在时频域上,单独的距离或者速度欺骗干扰,假目标距离和速度变化不匹配,与真实目标运动有差异,经数据后处理后,干扰得到抑制;在幅度上,真实目标回波幅度是有起伏变化的,而欺骗干扰幅度无此特性,数据后处理雷达通过提取真实目标和欺骗干扰信号的幅度起伏差异,实现对欺骗干扰信号的检测和抑制;在脉内调制方面,基于DRFM间歇采样转发干扰或者重复转发干扰,虽然能满足干扰的转发时延要求,但是干扰机在间隔采样过程中破坏了雷达信号脉内的调制特征,数据后处理雷达通过对回波信号脉内调制特征分析处理,可以很容易辨别出存在的干扰信号,并在后续过程对干扰信号进行抑制处理;其他处理域中的抗干扰方法。
在对数据后处理雷达进行干扰实验时发现,仅仅在功率上对回波目标产生压制,而不考虑干扰信号域目标信号的相关性,并不能对数据后处理雷达起到很好的干扰效果,因此,本节针对干扰信号在不同特征域的相关性要求,首先建立时频域协同干扰模型,然后对其添加方位和幅度控制,产生幅度、时域、频域、方位全相关的干扰信号。
1.1时频域协同相关干扰
设雷达发射的信号为s(t),目标以速度vr运行,经目标反射后,雷达接收的动目标回波可以表示为:
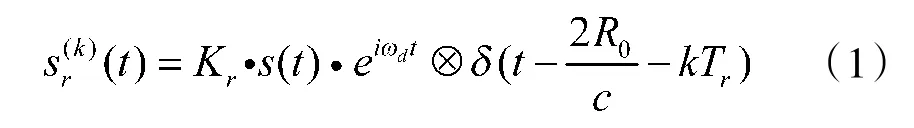
式中Kr为目标回波幅度,具有起伏特性,k为发射脉冲的序号,Tr为脉冲重复间隔(PRI),c为光速,ωd为目标运动引起的多普勒频移,R0为第k个脉冲发射时雷达距目标的瞬时距离。
自卫式干扰机在接收到雷达信号后,经过对雷达信号添加一定的延时函数Δt(t')和多普勒频移函数Δω(t')之后,再对干扰信号转发,形成时频域协同相关干扰回波表示为:
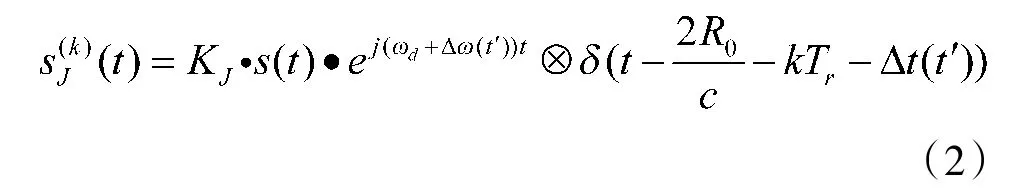
式中KJ是功率放大系数,一般为常数,取值是目标回波功率的1.3倍~1.5倍。
经过前面分析知道,干扰机所添加的延时函数和多普勒频移函数需要满足目标运动时的相关性,在具体实施时,当匀速拖引时,假设干扰时延函数为Δt(t'),根据时延函数可计算出对应的假目标距离ΔR(t'),假目标速度vJ,再由假目标速度vJ推导出与干扰时延函数相匹配的多普勒频移函数Δf (t'),时延函数和多普勒函数满足如下公式:
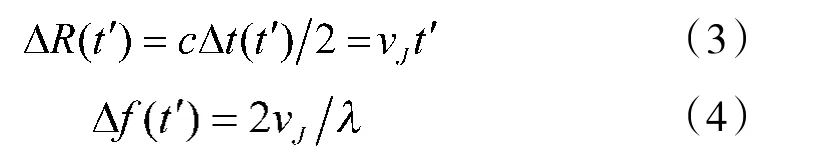
式中λ为雷达所用波长,其他参数的定义同之前。
同理匀加速拖引时,干扰时延函数和多普勒函数满足如下公式:

式中aJ是时延函数对应的假目标加速度。
出于安全考虑时频域协同相关干扰基本不用作随队干扰和近距离干扰。远距离支援干扰机因为干扰机与目标位置距离较远,干扰机在存储转发雷达信号延迟的基础上还要附加一定的时延调制,以抵消干扰机与目标距离因素产生的时延,干扰产生过程较复杂。自卫式干扰,干扰机位于机载目标上,干扰产生相对简单,容易进入雷达主瓣,节省了干扰功率。因此,时频域协同相关干扰主要用作自卫式干扰。
在具体实施时频域协同相关干扰时还必须考虑到数据后处理雷达可能采取的其他抗干扰措施[9],具体的应对方法如下页表1所示。
1.2时频域协同相关干扰的空间方位控制
时频域协同干扰实施后虽然造成了雷达对目标的距离、速度信息的错误跟踪,但假目标与真实目标仍处在同一方位上。当假目标距真目标很近时,如果此时敌方战斗机在该方向上发射导弹进行攻击,真实目标仍然存在被击中的可能,如图1所示。

表1 数据后处理雷达在时频域可能会采取的其他抗干扰方法和对应措施
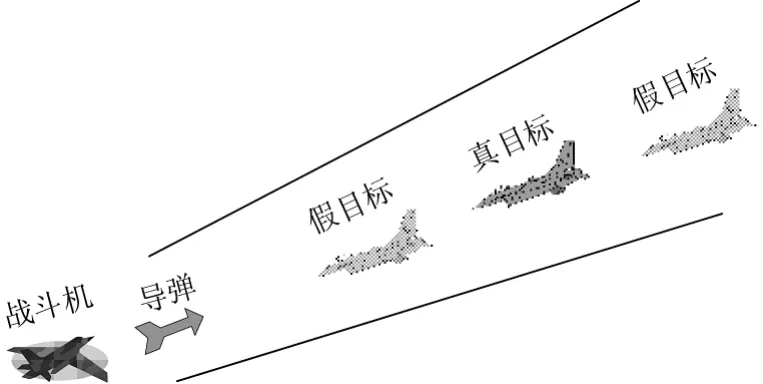
图1 导弹进攻假目标给真实目标带来的危险
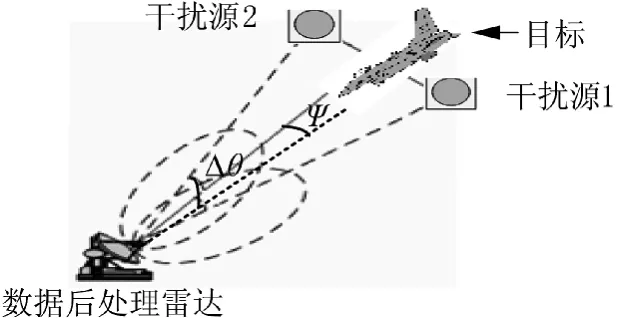
图2 时频域协同干扰方位控制实现方法
文献[10]考虑到这种危险,建立了结合方位信息的综合欺骗干扰方法。具体实施时,在载机末端装上两个干扰源,飞机右翼末端的接收天线接收到被袭雷达信号后进行移相+θ°,经DRFM处理放大α1倍后由左翼天线发射回雷达;与此同时,飞机左翼末端的天线接收到的雷达信号进行移相-θ°,经DRFM处理放大α2后从右翼上的天线发射出去,如图2所示,对于相干双点源干扰,误差角Ψ为:
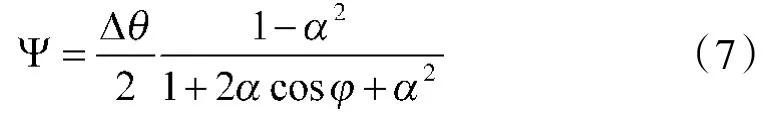
式中φ为两天线到达雷达天线口面的相位差:φ=2 θ,Δ θ为两干扰源O1和O2相对于雷达接收站的夹角,Δ θ一般小于接收站半功率波束宽度,α为两转发信号在雷达天线口面的振幅比:α1=α1/α2。
图3,图4分别是在Δθ=0.1°时,幅度比α和相位差φ取不同值时误差角Ψ的变化图。结果表明,当相位差120°<φ<240°,雷达到达角指向两天线以外且功率大的天线一侧,且当α≈1时误差角偏离载机的方向达到最大,达到方位欺骗效果,在实际干扰中φ的精确控制是十分困难的,一般灵活选择α对干扰效果进行控制。
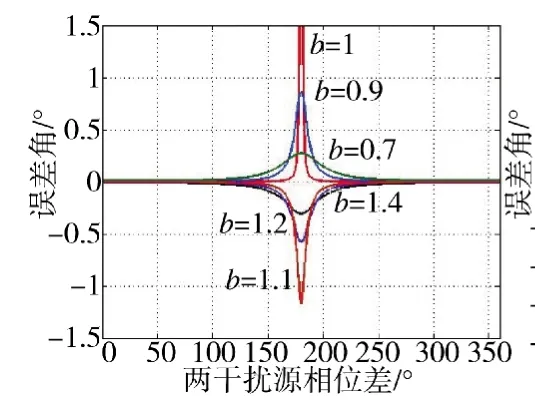
图3 误差角Ψ随相位差φ的变化关系
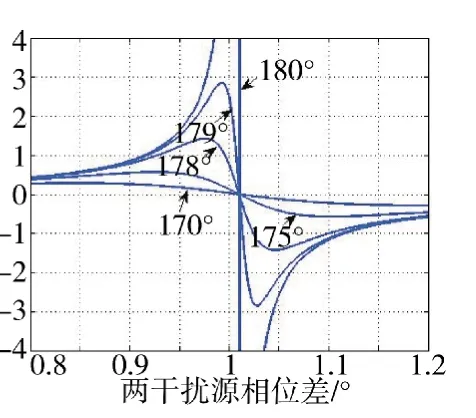
图4 误差角Ψ随幅度比b的变化关系
1.3时空频域协同相关干扰的幅度控制
真实目标回波幅度是有起伏变化的,常规的欺骗干扰幅度上只考虑功率大小而没有考虑幅度微动特性,数据后处理雷达通过提取真实目标和欺骗干扰信号的幅度起伏差异,实现对欺骗干扰信号的检测和抑制。为了破坏数据后处理雷达在幅度域的抗干扰能力,本节在产生的时频域协同干扰的基础上,进一步对其进行幅度控制,产生幅度域上具有起伏特性,时频域多参数协同相关的干扰信号。
根据幅度调制方式的不同,对欺骗干扰的幅度控制可以分为:数字域幅度控制和模拟域幅度调制,如图5、图6所示。
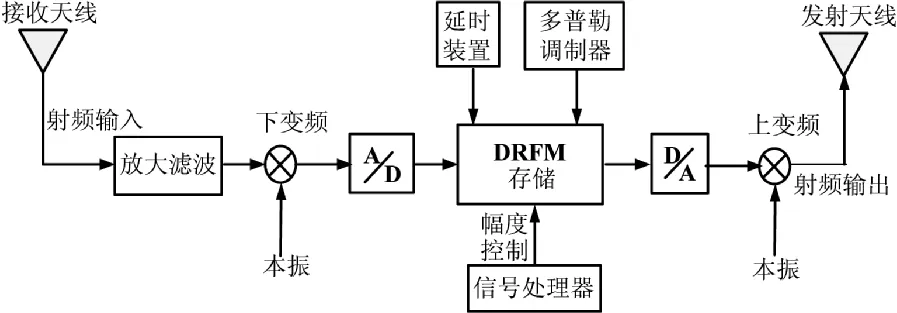
图5 数字域欺骗干扰的幅度控制原理框图
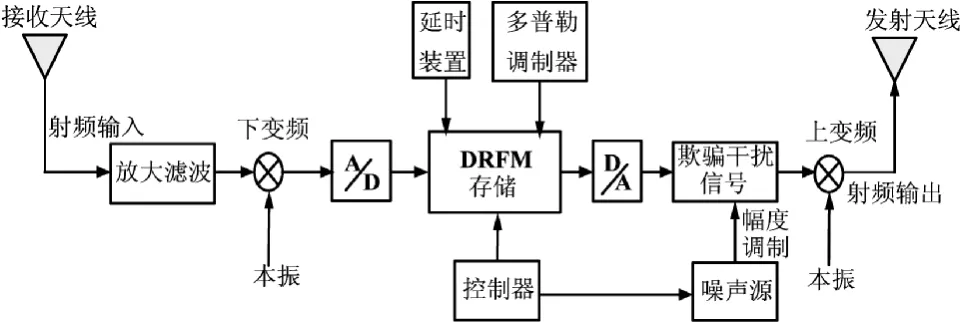
图6 模拟域欺骗干扰的幅度调制原理框图
图5中对欺骗干扰的幅度控制发生在D/A转化之前,因此,称作数字域幅度控制。截获的雷达信号经过滤波,下变频后,在A/D转化器中完成对基带信号的采样量化,并将结果保存在存储器中,这时干扰机根据对敌方雷达信号分析和掩护目标的运动姿态的观测,调整信号处理器中的控制码,完成对欺骗干扰的幅度控制。
图6是模拟域欺骗干扰信号幅度调制原理框图,DRFM控制噪声单元产生相应类型的噪声源,在调制器中完成对欺骗干扰的噪声幅度调制,通常选择高斯噪声作为调制信号。
根据式(2)将经过噪声幅度调制后的时频协同干扰信号表示为:
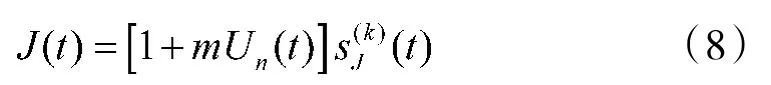
2相关干扰对雷达数据后处理能力的影响
2.1雷达数据后处理能力指标
根据引言中对数据后处理雷达抗干扰流程的表述可以看出,数据后处理雷达根据处理域的不同,数据后处理能力指标会有所不同:在幅度域上通常用回波的包络起伏差异作为指标,时频域中采用运动目标的时延-频偏匹配度作为后处理能力的指标,极化域采用极化差度作为指标,脉内调制域通常采用频率差度作为指标等等。本文主要考虑相关干扰在幅度域和时频域中对雷达数据后处理能力指标的影响。
2.1.1信号回波的包络起伏差异
在幅度域中,考虑动目标的情况,处于运动状态的目标(变速或匀速)会造成多普勒频移,并且会使雷达的观察视角发生变化,从而造成目标雷达截面积σ的起伏,σ通常符合Swerling模型,根据第1节中目标和干扰的回波模型,仅考虑目标和干扰回波的幅度,能够得到:
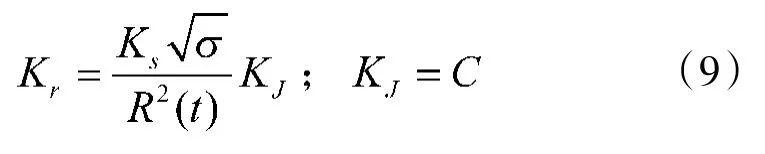
式中Kr、KJ分别为目标信号回波幅度和无幅度控制干扰信号幅度,Ks是跟天线增益,雷达发射功率,波长及雷达的各种损耗等相关的常数,R(t)为雷达和目标的瞬时距离,C为常数,以SwerlingII型进行分析,截面积σ的概率密度函数服从以下分布:
假设雷达接收到N个脉冲,将这N个脉冲的脉幅求均值和方差,作为所跟踪信号的幅度均值和方差。
因为σ和R(2t)相互独立,从而目标回波幅度的均值As和方差σs为:
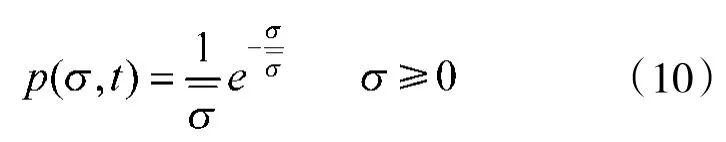
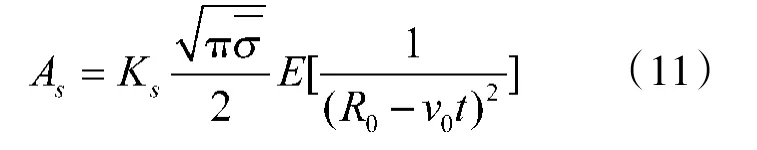
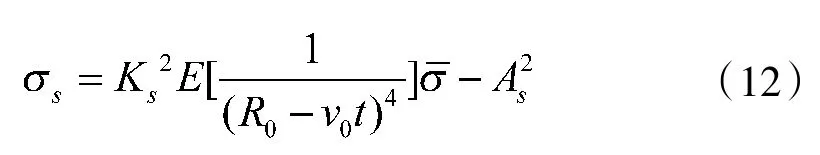
对于无幅度控制的欺骗干扰信号,其回波幅度的均值As和方差σs为:

式中γ表示雷达信号的幅度均值。
由式(8),对于幅度控制后的欺骗干扰信号,其回波幅度的均值Aj'和方差σJ'为:

作为雷达方经常采用信号瞬时包络的方差和均值共同表征包络起伏度作为幅度域上数据后处理能力指标,特征因子α表示如下:

2.1.2信号回波的时延-频偏匹配差异
在时频域中,对单独的距离拖引干扰或速度拖引干扰来说,干扰信号的时延与多普勒频移是不匹配的,数据后处理根据该特性通过设置时延-频偏匹配度,可以实现对单一欺骗干扰的识别与抑制。
以距离拖引干扰为例,假设干扰机时延函数ΔtJ(t')对应的虚假目标运动速度为vJ,则由式(3)可得vJ=cΔtJ(t')/2t';雷达通过速度波门测得目标运动的多普勒频移函数Δfr(t')求出对应的目标信号的速度为vr,由式(4)可得vr=λΔfr(t')/2。虚假目标运动速度vJ和真实目标的运动速度vr是不匹配的,存在差值,令ΔV=vr-vJ,当ΔV超过一定门限时,即认为有距离拖引干扰存在,取时延-频偏匹配度P=0,否则认为P=1。对于单独的速度拖引干扰以及经过幅度控制后的时空频协同相关干扰,可以采用上面同样的方法,通过干扰回波模型的分析,提取出对应的假目标和真实目标的速度差,在与门限比对后,最终确定时延-频偏匹配度P的取值大小,此处不再作详细分析介绍。
2.2相关干扰对数据后处理雷达干扰效果评估
数据后处理雷达通常采用不同处理域中数据后处理能力的联合指标表征雷达受到干扰前后接收波形的不同特征,根据本文中数据后处理雷达在幅度域和时频域后处理能力指标的分析,定义幅度域和时频域后处理能力联合指标ε,表示如下:
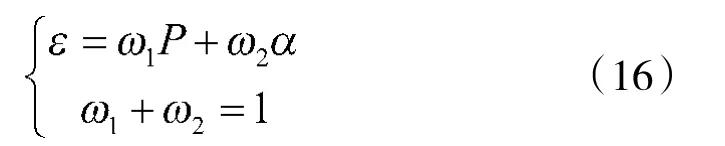
根据第1节中建立的回波模型,产生目标信号、无幅度控制时频协同干扰信号、幅度控制非时频协同干扰信号、无幅度控制非时频协同干扰信号、幅度控制时频域协同干扰各500个回波样本,依据ε的定义式,在相同信噪比(设为3 dB)下,目标回波信号与各干扰回波信号联合指标ε分布如图7~图10所示:
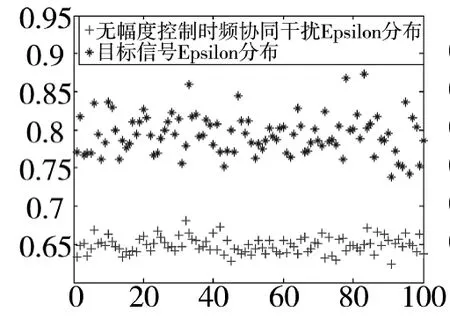
图7 目标回波与幅度不相关干扰的ε分布
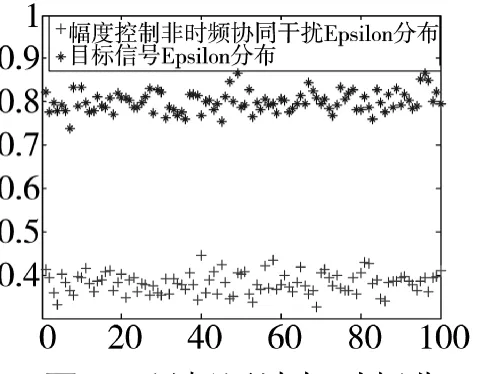
图8 目标回波与时频非相关干扰的ε分布
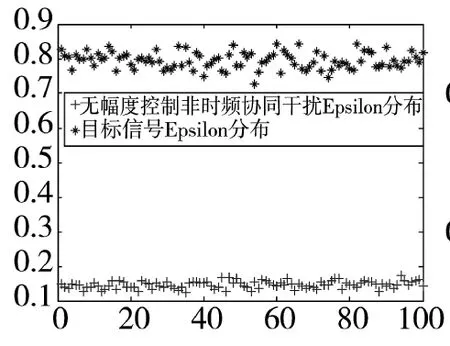
图9 目标回波与全不相关干扰的ε分布
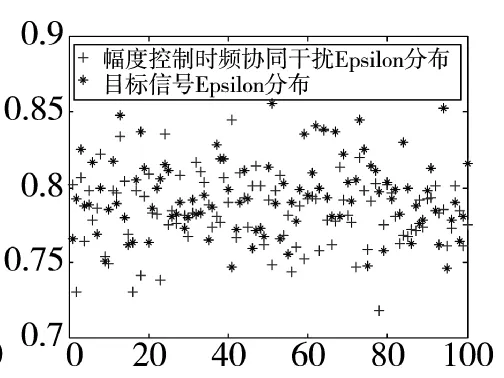
图10 目标回波与全相关干扰的ε分布
从图7~图9能看到目标回波与非相关干扰回波ε分布差异明显,且随着非相关程度的加大而增大,数据后处理雷达根据该特性很容易识别出干扰信号的存在。图10显示经过相关处理后的欺骗干扰与真实目标回波特征相似,能有效破坏雷达的后处理能力。
3仿真与分析
假设目标以v=200 m/s的速度匀速前进,雷达的照射截面积起伏全过程的均值σ¯=2 m2,雷达的脉冲重复间隔Tr=40 μs,假设目标距雷达最大作用距离Rmax时被发现R0=Rmax=c/2Tr=60 km。为便于数据计算,将目标距雷达R0时,雷达照射截面积σ¯=2 m2作为基准,将幅度与其相比以获得相对幅度,干扰信号的幅度是回波信号幅度的1.3倍。采用匀加速拖引,拖引加速度aJ=30 m/s2,波长λ=0.01 m,在拖引阶段随机采集数据,实验分4组进行,第1组分别产生目标回波信号和幅度非相关时频相关干扰信号各500次,按照本文所给方法提取特征因子,然后随机抽取800个数据作为训练样本,其余200个作为测试样本,采用BP神经网络设计分类器对信号进行分类检测。同理对第2组的幅度相关时频非相关干扰信号,第3组的幅度、时频均非相关干扰信号,第4组的幅度、时频均相关干扰信号以同样的方法进行分类检测,取SNR=3 dB,经过50次Monte Carlo实验,得到4组检测概率随N变化的曲线如图11~图14所示。
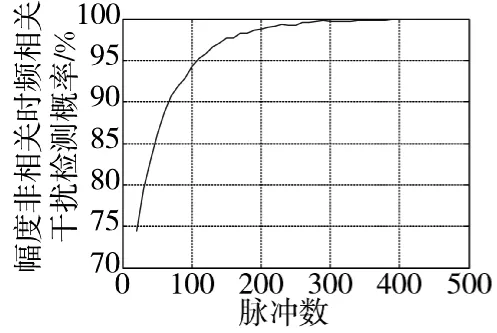
图11 幅度非相关时频相关干扰检测概率
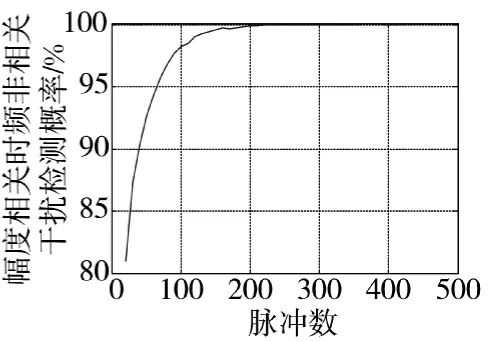
图12 幅度相关时频非相关干扰检测概率
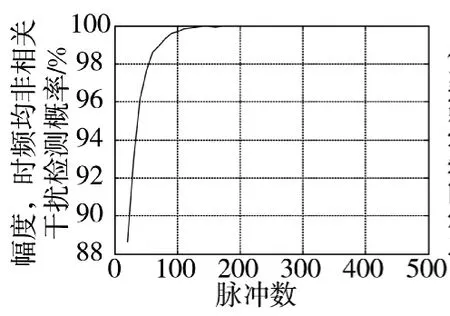
图13 幅度,时频均非相关干扰检测概率
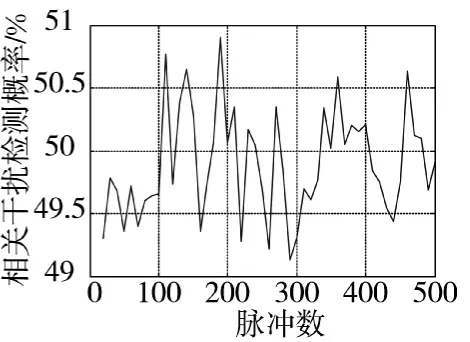
图14 全相关干扰的检测概率
从图11~图13可以看出,数据后处理雷达在对非相关干扰信号的检测时性能优越,利用提取的特征因子,对不同的非相关干扰均能够很快检测出干扰的存在,只是检测的时间快慢有所不同,而且非相关性越强,检测出干扰的时间越短。对于幅度、时频域均非相关的干扰信号,在脉冲积累次数达到120时就可以接近100 %识别出接收的干扰信号,检测结果趋于最优时所需的最短时间T=NTr=4.8 ms。
图14的结果显示,对相关干扰信号的检测概率始终处在50 %左右,雷达无法通过时频域以及幅度域上的数据后处理来区分出目标回波信号和干扰信号,本文设计的相关干扰可以对数据后处理雷达形成有效干扰欺骗。
4 结论
本文从数据后处理雷达抗干扰的原理着手,分别从时域、频域、空域方位和幅度域对数据后处理雷达的抗干扰性能和方式进行分析,然后提出各特征域的相关干扰。从文中分析能够看出为了对数据后处理雷达实施有效干扰,除了要保证干扰信号拥有足够的干扰功率,还需要产生的干扰信号雷达回波信号高度相似,即干扰信号与回波信号应在幅度域、空域、时域、频域具有全相关性。本文对数据后处理雷达干扰方式方法进行了初步探讨,并仿真验证了该方法的有效性,为数据后处理雷达的干扰提供了思路。
参考文献:
[1]李建勋,秦江敏,马晓岩.Kohonen网络用于雷达抗速度
欺骗干扰中的特征提取[J].雷达科学与技术,2004,2 (2):82-86.
[2]LI J X,SHEN Q,YAN H.Signal feature analysis and experimental verification of radar deception jamming[C]//IEEE CIE International Conference.Chengdu,2011.
[3]宁勇.对相控阵雷达旁瓣干扰方法研究[J].电子对抗,2009,129(6):1-7.
[4]李松,何劲.基于微多普勒效应的ISAR成像干扰新方法[J].宇航学报,2012,33(6):736-744.
[5]黄文韬,谭贤四.PD雷达抗噪声调幅干扰能力分析[J].舰船电子对抗,2010,33(2):22-26.
[6]潘小义,王伟.相干移频干扰幅度补偿技术研究[J].现代防御技术,2010,38(3):90-93.
[7]黄成家,刘晓东.机载PD雷达速度波门拖引干扰建模与评估[J].航天电子对抗,2010,26(4):47-50.
[8]孙智勇,唐宏.基于DRFM的机载PD雷达干扰研究[J].现代防御技术,2012,40(4):139-142.
[9]石晓娟,李明.基于DRFM的脉冲多普勒雷达组合干扰及其效能评估[J].电子信息对抗技术,2006,21(6):34-38.
[10]尚志刚,白渭雄.对PD雷达进行综合欺骗干扰研究[J].火力与指挥控制,2013,38(1):91-93.
Research on Technologies for Multi-parameter Collaborative Coherent Jamming Against Data Post-Processing Radar
LIU Xiang,WANG Jie-gui,MENG Xiang-hao
(Electronic Engineering Institute,Hefei 230037,China)
Abstract:Although the interference signal transmitted by DRFM has a high jamming power,the false target generated by DRFM is not related to real target.Data post-processing radar can use this feature to detect and eliminate the deception jamming.For its superior performance in suppressing non-coherent jamming,a coherent jamming signal modal is proposed in this paper which can ensure the effectiveness of the interference signal,according to the different requirements in different feature domains.It has fluctuated amplitude and also is designed to be coherent in time-frequency domain and direction.Finally,compared with the non-coherent jamming,simulation results verify the effectiveness and correctness of the proposed method.
Keywords:time-frequencydomaincollaborativejamming,amplitudecontrolling,directioncontrolling,data post-processing ability indicator
作者简介:柳向(1989-),男,河南商丘人,硕士研究生。研究方向:雷达及雷达对抗理论与技术。
*基金项目:国家自然科学基金资助项目(60801044)
收稿日期:2015-02-25修回日期:2015-04-27
文章编号:1002-0640(2016)03-0031-05
中图分类号:TN973
文献标识码:A

