输入受限的网络Euler-Lagrange系统有限时间一致性

袁利毫, 罗礼勇,2, 昝英飞, 李新飞

(1.哈尔滨工程大学 船舶工程学院, 黑龙江 哈尔滨 150001； 2.黑龙江大学 数学科学学院, 黑龙江 哈尔滨 150001)



输入受限的网络Euler-Lagrange系统有限时间一致性

袁利毫1, 罗礼勇1,2, 昝英飞1, 李新飞1

(1.哈尔滨工程大学 船舶工程学院, 黑龙江 哈尔滨 150001； 2.黑龙江大学 数学科学学院, 黑龙江 哈尔滨 150001)

摘要：针对网络Euler-Lagrange系统的有限时间协调一致性问题，考虑控制力矩有界和速度信息不可测的实际情况。基于有限时间控制技术，利用双曲正切函数，设计出了网络Euler-Lagrange系统分布式有限时间一致性控制算法。利用代数图论、Lyapunov稳定性理论和齐次性理论，证明了设计出的控制算法能够使得所有智能体的位置和速度在有限时间内达到一致,并且满足控制力矩有界的条件。最后数值仿真结果表明在控制力矩有界和速度信息不可获取的情况下，所设计出控制算法的有效性和可行性。

关键词：Euler-Lagrange系统；有限时间；速度信息不可测；一致性算法

由于Euler-Lagrange方程能够建模大量的机械系统,如操作机械臂[1-4]、水下机器人[5-9]等。对网络Euler-Lagrange系统(NELS)协调控制的研究有着重要的理论价值和实际意义。Liu等[10]在切换拓扑结构中,利用分布式自适应控制方法研究了含通信时延的NELS的一致性。Min等[11-12]分别考虑了参数不确定的NELS分布式自适应协调一致性问题和带耦合时滞的多Lagrange系统的状态一致性。在有向通信拓扑结构中,Liu等[13]研究了一组参数不确定的NELS自适应一致性，设计了三种情况下系统的分布式自适应协调一致算法。Yang等[14]研究了NELS的鲁棒同步跟踪控制问题,针对系统的低耦合不确定性问题提出了一种新的分布式滑模控制方案。Liu等[15]研究了NELS编队跟踪控制,同时针对了外界噪声干扰和执行器故障两种情况,设计的控制方案保证了跟随者状态跟踪到领航者。

与渐近收敛相比较,有限时间收敛具有更好的收敛性能,能够使系统具有快速、精确跟踪等优点。Liu等[16]在无向拓扑结构中考虑了无领航者的NELS一致性,设计的分布式控制算法保证系统状态在有限时间里达到一致。Aldana等[17]在无向拓扑结构中研究了用Euler-Lagrange方程描述的异质机器人的一致性问题,同时考虑了是否存在领航者的两种情况。Yu等[18]采用终端滑模控制方案,研究了机械臂有限时间协调跟踪控制。Su等[19]考虑了由Lagrange方程建模的机器人系统分布式有限时间协调跟踪控制问题。

本文针对控制力矩有界的NELS分布式有限时输出反馈控制问题进行了研究，提出了NELS的分布式有限时间一致性算法。与文献[16]相比较，本文的创新点在于：1) 论文在速度不可测的情况下，通过构造动态滤波器来实现无需速度信息的网络Euler-Lagrange系统有限时间一致性；2) 设计的控制算法在控制力矩先验有界时，能够使得系统在有限时间里达到一致。

1非线性控制方法

1.1 网络Euler-Lagrange系统模型

假设第i个智能体Lagrange系统的动力学模型由如下Euler-Lagrange方程建模：

(1)

式(1)有下面两个重要的性质：

(2)

1.2代数图论

利用图论基础知识来表示n个智能体之间的信息交。假设图G={v,ε}是含有n个节点的通信拓扑结构图,v={v1,v2,…,vn}为节点集,ε={e1,e2,…,en}为边集。 若(vi,vj)∈ε表示顶点vj能够获取顶点vi的信息,同时把vj称作vi的子节点,vi叫做vj的父节点。在无向拓扑结构图中(vi,vj)∈ε等价于(vj,vi)∈ε。图G是连通的,若满足条件使得G中任意两个顶点之间都有一条边能够将其连接。设A=[aij]∈Rm×m为图G的加权邻接矩阵,其元素aij定义为：当(vi,vj)∈ε时,aij>0,否则aij=0。

1.3非线性稳定性定理

定义1[4]考虑如下系统

(3)

式中：f:U0→Rm,f(x)=[f1(x)f2(x) …fm(x)]T是一个连续的向量场函数。设(r1,r2,…,rm)∈Rm，其中rp>0,p=1,2,…,m,若对任意的ε>0,满足fp(εr1x1,εr2x2,…,εrmxm)=εk+rpfp(x),∀x∈Rm成立,则称f(x)关于(r1,r2,…,rm)是齐次度为k∈R的齐次函数。如果f(x)是齐次的,则有系统(3)是齐次的。

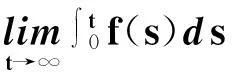
引理2[21]考虑如下系统

(4)

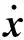
(5)

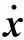
1.4符号定义

为了方便，对x=[x1…xn]∈Rm，0<α<1，首先定义sig(x)α=[|x1|αsgn(x1)…|x1|αsgn(x1)]，其中sgn(·)为符号函数。

2控制算法设计

考虑系统式(1),针对速度不可测问题,设计控制力矩有界的分布式一致性算法τi,使得系统在有限时间里,满足如下控制目标：

(6)

式中：ξi为辅助变量，用于估测速度，t大于T,且T为一大于零的固定数。

为实现系统(1)的有限时间一致性,设计如下分布式有限时间一致性算法：

(7)

(8)

其中，对任意的y→0时，有tanh(y)=cly+o(y)，cl为正常数，l=1,2，o(y)为y的高阶无穷小量，ki、λi是大于零的常数,aij是邻接矩阵A的(i,j)位置元素，α1=α2/(2-α2)。

证明 1)证明系统(1)在控制算法(7)、(8)作用下的全局渐近稳定性，选取如下Lyapunov函数：

(9)

计算V对时间t求导，将式(7)、(8)代入式(9)整理可得:

(10)

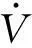
(11)

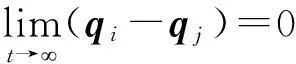
2)为证明系统(1)在(7)、(8)局部有限时间稳定,首先定义:

于是,系统(1)在算法(7)～(8)下可以改写成如下形式：

(12)

其中：

同样,通过选取如下Lyapunov函数：

tanh(sig(s)α1)ds

(13)

接下来推导

(14)

(15)

3)证明所有控制力矩都有界，对任意常数c>0和向量x∈Rm，有‖tanh(cx)‖≤1,则控制力矩的界‖τi‖。因此,如果,则有‖τi‖≤τMi。

注1针对系统(1),当系统能够获取自身速度信息时，可设计如下分布式有限时间一致性算法：

(16)

式中:kpi、kdi为正实数，0<α1<1,α1=α2/(2-α2)。

注2在分布式有限时间一致性算法(7)、(8)中当α1=α2=1时,可得到如下渐近收敛的控制算法：

(17)

(18)

其中,ki、λi与算法(7)、(8)中定义相同。

3数值仿真

为了检验系统(1)在算法(7)、(8)下的有效性，基于MATLAB/Simulink环境，搭建数值仿真模

型来进行仿真验证。考虑由4个机械臂组成的系统，其相互间的通信拓扑结构如图1所示。

假设4个机械臂具有如下Euler-Lagrange方程建模的动力学模型：

式中：

cos(q2-αe)+J1+J2

g1=(m1l1+m2l1)gcos(q1)+m2l2gcos(q1+q2)

g2=m2l2gcos(q1+q2)

其中，机械臂连杆质量为m1=1.2、m2=1.5,两连杆间长度为l1=1.0、l2=0.8,其接点到质心距离为lc1=0.6、lc2=0.7,两连杆之间的转动惯量为J1=0.35、J2=0.4、g=9.8m/s2、αe=30°。选取ki=3、λi=5、α1=2/3、α2=4/5。

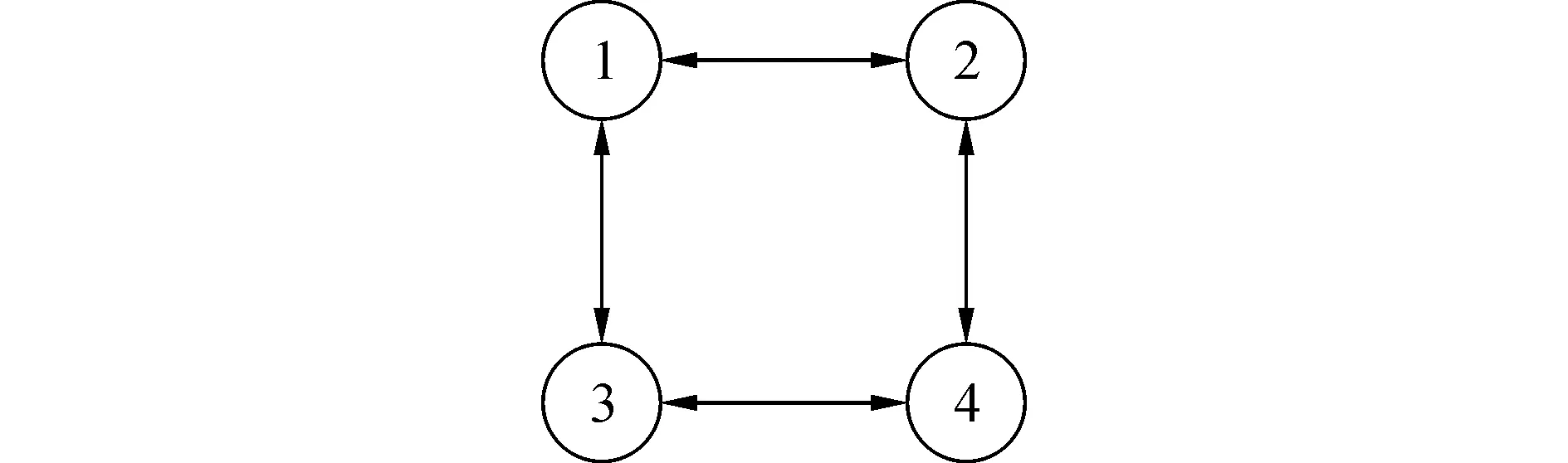
图1　4个机械臂间的拓扑结构图Fig.1　The topology associated with four manipulators

仿真结果如图2～4所示。图2与图3分别表示各机械臂的位置和速度变化曲线，从图2、图3可以看出在有限时间里四个机械臂的位置和速度均能达到一致。图4表示控制力矩随时间的变化曲线，从图4中看出控制力矩的上界τi=10。数值仿真结果与理论相一致，表明了提出的控制算法的正确性。

(a) q(1)组位置变化曲线　　　　　　　　　　　　　(b) q(2)组位置变化曲线图2　4个机械臂之间的两组位置变化Fig.2　Two groups of positions for the four manipulators

(a) q(1)组速度变化曲线　　　　　　　　　　　　　(b) q(2)组速度变化曲线图3　4个机械臂之间的两组速度变化Fig.3　Two group of the velocity for the four manipulators

(a) q(1)组控制力矩变化曲线　　　　　　　　　　　　　(b) q(2)组控制力矩变化曲线图4　4个控制力矩两组变化曲线Fig.4　Two groups time history curves for the four controller

4结论

1)基于齐次性理论，给出了NELS全局有限时间稳定的充分条件，通过利用饱和函数和构造动态滤波器实现了控制力矩有界和速度信息不可测的NELS有限时间一致性。

2)数值仿真结果表明了NELS建模的各机械臂位置和速度都在有限时间内达到一致，控制力矩存在上界，表明了NELS分布式有限时间控制算法的有效性和可行性。

3)进一步考虑外界干扰等实际情况，利用滑模控制等方法研究基于Euler-Lagrange方程建模的水下多机器人系统编队协调控制问题。

参考文献：

[1]LI Zhijun, LI Jianxun, KANG Yu. Adaptive robust coordinated control of multiple mobile manipulators interacting with rigid environments[J]. Automatica, 2010, 46(12): 2028-2034.

[2]VALENTIN F, TOBIAS M, ALEXANDER H, et al. Dynamic modeling of constant curvature continuum robots using the Euler-Lagrange formalism[C]// IEEE International Conference on Intelligent Robots and Systems, USA, Chicago, 2014: 2428-2433.

[3]JIN Maolin, LEE J, CHOI C. Practical nonsingular terminal sliding-mode control of robot manipulators for high-accuracy tracking control[J]. IEEE transactions on industrial electronics, 2009, 56(9): 3593-3601.

[4]HONG Yiguang, XU Yangsheng, HUANG Jie. Finite-time control for robot manipulators[J]. Systems and control letters, 2002, 46(4): 243-253.

[5]WU Xiaofeng, WU Zewei, CAI Jianping. Recovery control for the parent-child autonomous underwater vehicles via a master-slave synchronization scheme[C]// The 33rd Chinese Control Conference. Nanjing, China, 2014: 1317-1320.

[6]CHEN Weichen, JEN S K, JING F T. Modeling and simulation of an AUV simulator with guidance system[J]. IEEE journal of oceanic engineering, 2013, 38(2): 211-225.

[7]CORINA B, MATTHEW W, DUNNUGAN Y P. Dynamic coupling and control issues for a lightweight underwater vehicle manipulator system[C]// IEEE The 2014 Oceans-St. John's, St. John's, NL, 2014: 1-6.

[8]EVEV B, KRISTIN Y. P. Formation control of 6-DOF Euler-Lagrange systems with restricted inter-vehicle communication[C]// IEEE Conference on Decision and Control Manchester Grand Hyatt Hotel, San Diego, CA, USA, 2006: 5718-5723.

[9]JONGHOON P, WANKYUN C. Nonlinear H∞optimal PID control of autonomous underwater vehicles[C]// IEEE International Symposium on Underwater Technology, Tokyo, Japan, 2000: 193-198.

[10]LIU Yuan, MIN Haibo, WANG Shicheng. Distributed adaptive consensus for multiple mechanical systems with switching topologies and time-varying delay[J]. Systems and control letters, 2014, 64(2): 119-126.

[11]MIN Haibo, SUN Fuchun. Distributed adaptive consensus algorithm for networked Euler-Lagrange systems[J]. IET Control theory and applications, 2011, 5(1): 145-154.

[12]MIN Haibo, WANG Shicheng, SUN Fuchun. Robust consensus for networked mechanical systems with coupling time delay[J]. International journal of control, automation, and systems, 2012, 10(2): 227-237.

[13]LIU Jun, JI Jinchen ZHOU Jin, et al. Adaptive group consensus in uncertain networked Euler-Lagrange systems under directed topology[J]. Nonlinear dynamics, 2015, 82(3): 1145-1157.

[14]YANG Zijiang, QIN P. Distributed robust control for synchronized tracking of networked Euler-Lagrange systems[J]. International journal of systems science, 2015, 46(4): 720-732.

[15]LIU Lei, SHAN Jinjun. Distributed formation control of networked Euler-Lagrange systems with fault diagnosis[J]. Journal of the Franklin Institute, 2015, 352(3): 952-973.

[16]刘源, 王仕成. 无领航者的多Euler-Lagrange系统有限时间一致性算法[J]. 控制理论与应用, 2014, 31(1): 93-99.

LIU Yuan, WANG Shicheng. Decentralized finite-time leaderless consensus algorithm for networked Euler-Lagrange systems[J]. Control theory and applications, 2014, 31(1):93-99.

[17]ALDANA C, NUNO E, BASANEZ L. Operational space consensus of multiple heterogeneous robots without velocity measurements[J]. Journal of the franklin institute, 2014, 351(3): 1517-1539.

[18]YU Shuanghe, YU Xinghuo, et al. Continuous finite-time control for robotic manipulators with terminal sliding mode[J]. Automatica, 2005, 41(6): 1957-1964.

[19]SU Yuxin, SWEVERS J. Finite-time tracking control for robot manipulators with actuator saturation[J]. Robotics and computer-integrated manufacturing, 2014, 30(2): 91-98.

[20]SLOTINE J, LI Weiping. Applied nonlinear control[M]. New York: Prentice Hall, 1991.

[21]MENG Ziyang, REN Wei, YOU Zheng. Distributed finite-time attitude containment control for multiple rigid bodies[J]. Automatica, 2010, 46(12): 2092-2099.

Finite-time consensus control for networked Euler-Lagrange systems with input saturations

YUAN Lihao1, LUO Liyong1,2, ZAN Yingfei1, LI Xinfei1

(1. School of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China; 2. School of Mathematical Science, Heilongjiang University, Harbin 150001, China)

Abstract：This article focuses on the finite-time coordinated consensus problem for networked Euler-Lagrange systems with control torque constraints and the velocity is not available for feedback. Based on the finite-time control technology, by using hyperbolic tangent function, a velocity-free distributed finite-time consensus algorithm is designed for velocity is not measurable and the control inputs are regarded as a priori bounded. Rigorous proof shows that the positions and velocities of all agents can be achieved consensus in finite-time and the control scheme satisfies the control torque constraints requirement with the algebraic graph theory, homogeneous method and Lyapunov stability theory. Finally, numerical simulation validates the effectiveness and feasibility of the proposed method with control torque constraints and without velocity measurements.

Keywords：Euler-Lagrange systems; finite-time; without velocity measurements; consensus algorithm

中图分类号：TP273

文献标志码：A

文章编号：1006-7043(2016)02-0157-06

doi:10.11990/jheu.201512037

作者简介：袁利毫(1982-), 男, 讲师, 博士.通信作者：袁利毫, E-mail：yuanlihao82@163.com.

基金项目：国家科技重大专项资助项目(20112X05027).

收稿日期：2015-12-11.网络出版日期：2016-01-25.

网络出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20160125.1638.002.html