临坡双层粘土地基极限承载力的上限分析*1

胡卫东，曹文贵，袁青松

(1. 湖南大学 岩土工程研究所，湖南 长沙　410082；2. 湖南理工学院 土木建筑工程学院，湖南 岳阳　414000)



临坡双层粘土地基极限承载力的上限分析*1

胡卫东1,2†，曹文贵1，袁青松1

(1. 湖南大学 岩土工程研究所，湖南 长沙410082；2. 湖南理工学院 土木建筑工程学院，湖南 岳阳414000)

摘要：在现有研究基础上，结合临坡条形基础双层粘土地基临近边坡的非对称性特征和层状地基特征，构建出临坡条形基础双层粘土地基的多滑块组合单侧滑移破坏模式；根据速度相容关系和速度三角形闭合条件，确定出多滑块离散模式相对应的机动允许速度场；引入上限极限分析理论，导出临坡条形基础双层粘土地基极限承载力计算模型，在此模型上采用序列二次规划算法进行优化求解，建立了临坡条形基础双层粘土地基极限承载力确定方法.利用Matlab的符号运算功能和优化函数编程计算进行实例分析，并与有限元数值计算结果进行对比分析，表明了本文研究方法的可行性与合理性.

关键词：临坡地基；双层粘土地基；上限分析；条形基础；极限承载能力

目前，均质浅基础地基的承载力问题已经有了较深入研究，但实际上工程大部分地基都是非均质层状地基，土层之间的力学指标差别较大，使得成层土地基与均质土地基在破坏机理和破坏模式上有着显著不同，其相应地基极限承载力也必然存在较大差别，因此，开展成层土地基承载力确定方法的研究有着重要的工程意义，这也正是本文研究的出发点.

由于受到土层厚度和力学强度指标等的影响，成层土地基的破坏模式更加复杂，给成层土地基承载力确定方法的研究造成了较大困难，尽管如此，不少学者通过长期研究，在成层土地基承载力确定方法方面取得了长足的进步，形成了包括极限平衡法、滑移线法、极限分析法和数值分析法等多种研究方法[1-11].然而，已有成层土地基承载力确定方法的研究仍然存在一定程度的问题和不足，如Hasen[1]加权平均法取有效深度范围内不同土层厚度的加权平均强度后直接用于均质土的Hasen公式，其方法由于简单实用得到了较为广泛的运用，但仍然只是一种半经验方法；Meyerhof和Hanna[2]提出的剪切理论认为上部土层发生冲剪破坏，下部土层发生整体剪切破坏，经过大量模型试验检验该理论运用于成层土地基极限承载力计算具有一定合理性，但只能解决硬土层下卧软土层地基承载力问题；杨永新[3]等基于滑移线场理论，研究了极限平衡区中上层粉土和下层砂土的地基承载能力，其研究方法的适应性仍受到一定限制；Zhu[4]等及Burd和Frydman[5]等采用数值分析方法能有效解决复杂边界问题和非均质土层问题，但由于土体强度参数选择的困难，也并没有在实际工程应用中被广泛接受；Florkiewxicz[6]等基于极限分析上限理论，采用多滑块组合破坏模式研究双层和三层非水平分层地基的极限承载力，经过与其它理论研究方法结果和实验结果的对比分析，验证了其正确性和有效性；Michalowski[7]等采用折线间断面形式构建了无粘性土下卧饱和软粘土双层地基的机动速度场，对比分析了多种破坏模式的适用性，但是上述两者确定的机动速度场实际应用到临坡地基当中仍有待进一步改进.

近年来，临近斜坡浅基础下层状粘土地基广泛出现在各类岩土工程结构中，但就目前来说，从临坡地基出发开展临坡层状粘土地基破坏模式和承载力性状的研究还不够深入.已有的临坡均质粘土地基破坏模式大多假定滑动面为圆弧或对数螺旋线[12]，但现实情况下，由于斜坡的存在和层状构造土的性质各异，临坡层状粘土地基应力-应变分布极为复杂，使得其在地基破坏模式上与临坡均质粘土地基相比已发生了很大改变，层状地基越不均质，真正的最危险滑动面偏离圆弧滑动面越远，而且也并非对数螺旋线就能逼近真实滑动面，因此，临坡层状粘土地基的任意滑动面形状的确定尤为重要.采用多滑块组合破坏模式的上限极限分析方法，无需事先对极限状态下的连续滑动面形状做出各种假设，能有效结合地基临近斜坡和层状构造的特征，真实反映层状地基粘土重度、粘聚力、土层厚度、埋深和坡角等不同影响因素作用下的破坏模式，而且，上限极限分析方法能避免对滑块间作用力过多假设，不需考虑土体复杂的应力-应变关系且理论严谨，这就为临坡成层土地基承载力确定方法的研究提供了一条有效的研究途径，这也正是本文研究的重要内容之一.

为此，本文将从临坡条形基础双层粘土地基破坏模式研究入手，在考虑基础埋深和临坡距离等影响的基础上，采用多滑块组合破坏模式，利用上限极限分析方法，构建临坡条形基础双层粘土地基机动允许的速度场，建立新的临坡条形基础双层粘土地基极限承载力分析模型，以期完善临坡地基承载力分析的理论与方法.

1临坡双层粘土地基破坏模式

已有研究成果表明，采用单侧滑动破坏模式的临坡地基极限承载力分析方法往往较为保守和安全[13]，为此，本文假设临坡条形基础双层粘土地基在均布极限荷载Qu作用下，沿ACD滑动破坏面发生单侧滑动破坏，如图1所示.

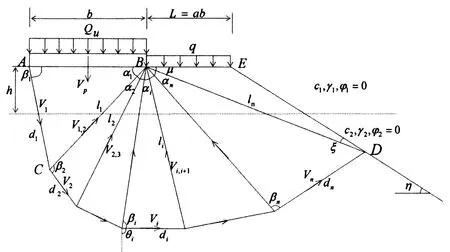
图1　临坡条形基础双层粘土地基破坏模式

上述即为本文确定的临坡条形基础双层粘土地基的多滑块组合破坏模式，根据图1中的几何关系，刚性三角形多滑块破坏几何模型实际由2n个几何可变参量αi，βi(i=1,…,n)确定，其它参量如li，di，Si(i=1,…,n)等均可由以上可变参量求得，其具体分析过程如下：

(1)

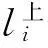
(2)

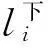
(3)

三角形滑块底边边长di其大小可表示为：

(4)

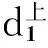
(5)

(6)

沿滑动面上n个三角形滑块的面积，其大小可表示为:

(7)

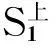
(8)

(9)

(10)

(11)

式中i=2,…,n.

斜坡顶面水平，条形基础外侧边缘距坡顶距离L可用距离比系数a表示，则有:

L=ab

(12)

斜坡表面为直线，具有足够延伸长度，斜坡倾角为η，于是，斜坡上第n+1个三角形被动滑块BDE的刚体几何形状即可确定，其三角形滑块两个底角μ和ξ及面积SBDE均可由以上几何参量表示.

(13)

(14)

(15)

至此，构建出了临坡条形基础双层粘土地基多刚性滑块组合的几何破坏模型，该分析模型较好地反映了临坡双层地基临近边坡的非对称性特征和双层地基层状特征，为本文采用极限分析方法确定临坡条形基础双层粘土地基极限承载力奠定了坚实基础.在此基础上，为了保证单侧滑移几何破坏机构成立，刚性滑块的几何变量还应满足以下边界约束条件：

(16)

滑动破坏面ACD需满足破坏面上凹的限定，即

0<θ1<θ2<…<θi<…<θn<π

(17)

式中θ表示边界滑动面线段顺时针方向旋转至向下垂直线的夹角(如图1所示).

同时刚性三角形滑块BDE还须满足以下几何约束条件

(18)

上式亦可表示为约束方程

(19)

2机动允许速度场的建立

临坡双层粘土地基破坏机构机动允许速度场的构建是采用极限上限分析方法确定临坡地基承载力必须解决的关键问题，为了确定允许速度场，首先做如下假定：

1)临坡地基为水平层状地基，持力层范围内有两层饱和粘土，采用不排水剪有效粘聚力，内摩擦角φ1=φ2=0.

2)条形基础基底与地基土间允许产生相对滑动，基础以速度VP垂直向下运动.

3)临坡粘土地基服从Mohr-Coulomb屈服准则和相关联流动法则.

在上述假设基础上，根据速度相容的闭合三角形几何关系，可得到如图 2所示速度关系和图3所示破坏机构的机动允许速度场[16]，再由矢量分析原理及速度相容性要求可以推导出各速度间断面上速度.

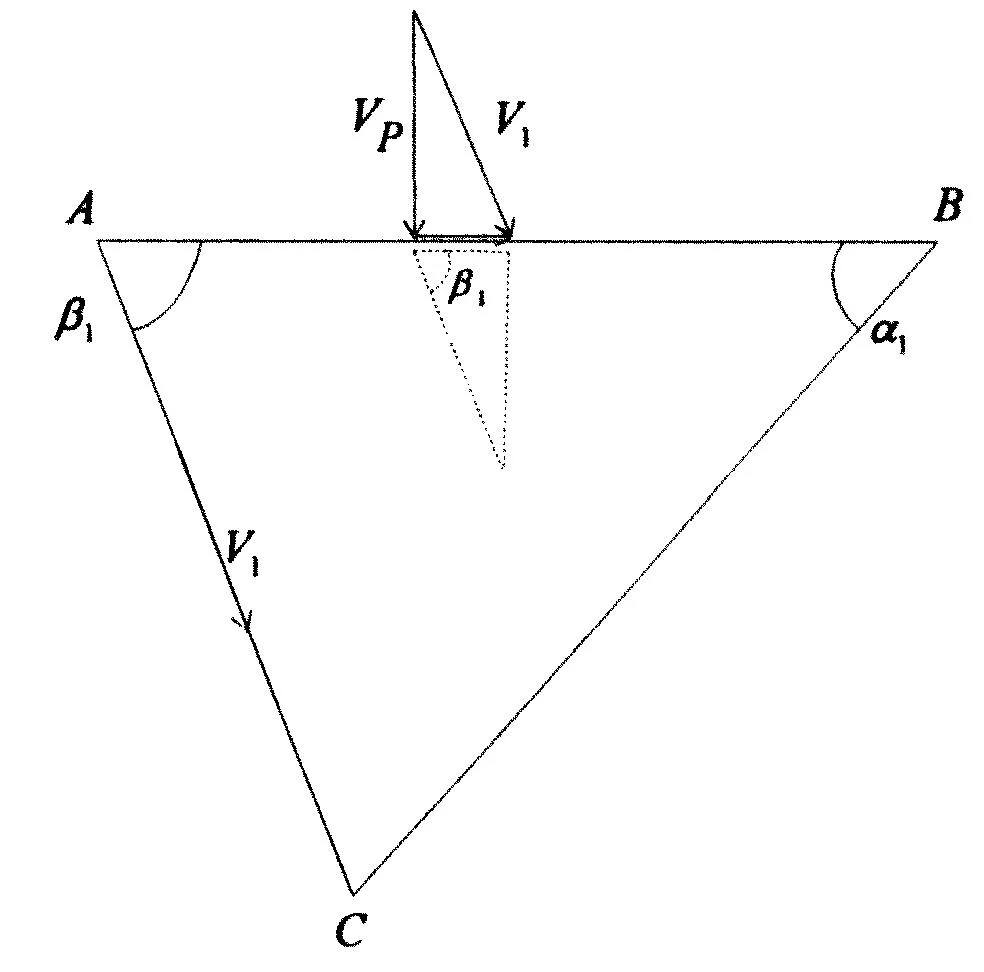
图2　速度关系

1)由图2 所示速度关系，根据速度相容关系，条形基础运动速度方向垂直向下，其大小可表示为:

VP=V1sinβ1

(20)

式中V1表示滑块1斜向下的运动速度，考虑到AC为速度间断面，V1实际为AC面上的间断速度.

2)根据图3所示破坏机构的机动允许速度场，刚性滑块在运动中不产生重叠和扭曲畸变，满足相容速度闭合的三角形几何关系，由此可计算各速度间断线上的速度[17]，滑动破坏面ACD即各三角形滑块底边上间断速度Vi实际方向为沿滑动面切向方向，其大小可表示为：

(21)

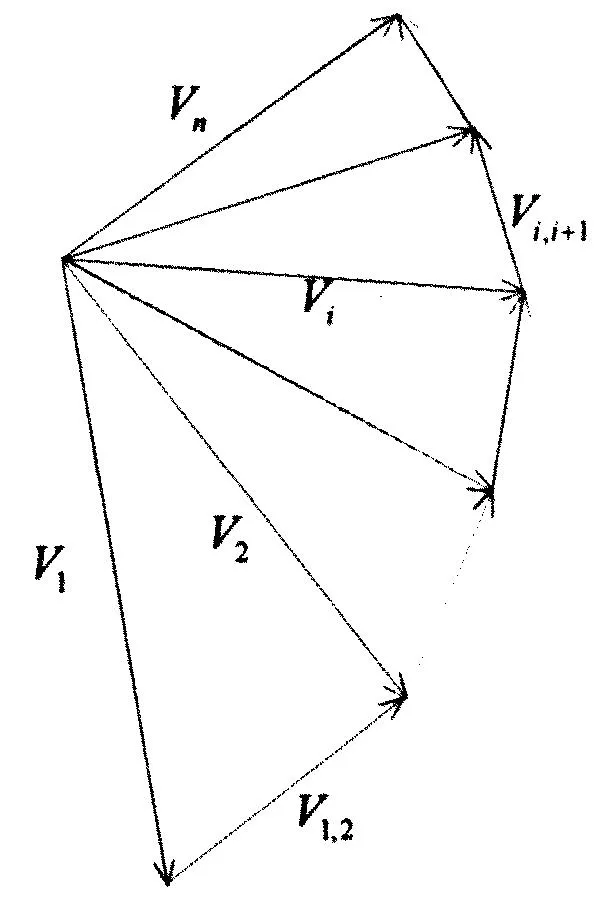
图3　破坏机构相应允许速度场

各三角形滑块间接触面间断速度Vi,i+1方向为沿滑块间接触面切向方向，其大小可表示为:

(22)

3)斜坡上刚性滑块BDE为被动滑块体，考虑到各刚性滑块之间挤压运动必然具备连续性的特点，滑块BDE的运动速度与第n号滑块体上速度Vn不仅方向完全相同，大小也相等，因此，BD面两侧速度连续，BD面不是速度间断面，BD面上没有能量耗散.

3能量耗散率的计算

3.1外力功率

本文研究问题的外力包括考虑埋深引起的分布力q、基底极限压力Qu及各滑体自重力，各外力功率具体计算方法如下：

1)q外力功率Wq

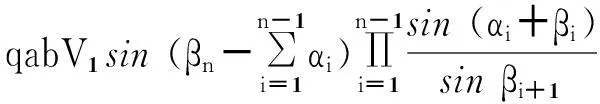
(23)

式中q为基础外侧坡顶面由于埋深作用的竖向均匀分布压力，不计基础埋深内土体抗剪强度对地基极限承载力的影响，则其值可用式(24)表示

q=γ1H

(24)

式中γ1为第1层粘土即埋深内地基土体重度；H为基础的埋置深度.

2)Qu外力功率WQu

WQu=QubV1sinβ1

(25)

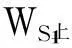
(26)

(27)

式中γ2为第2层粘土重度.

(28)

(29)

式中i=2,…,n.于是，第1层粘土地基其余滑块受自重外力总功率为

(30)

式中：

(31)

第2层粘土地基其余滑块受自重外力总功率为：

(32)

式中：

(33)

5)斜坡上滑块BDE自重外力功率WSBDE

(34)

将式(1)和式(15)代入，经化简，可得

(35)

于是，总的外力功率W为:

(36)

3.2内能耗散率

本文研究问题的内能耗散率包括各滑块间速度间断面和破坏间断面ACD的能量耗散率，具体分析方法如下：

(37)

式中i=1,…,n-1;c1为第1层饱和粘土有效粘聚力.于是，第1层粘土地基滑块间速度间断面总能量耗散率为:

(38)

式中：

(39)

(40)

式中i=1,…,n-1;c2为第2层饱和粘土有效粘聚力.于是，第2层粘土地基滑块间速度间断面总能量耗散率为：

(41)

式中：

(42)

2)AC间断面能量耗散率Dd1

(43)

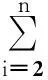
(44)

于是，总的内能耗散率D为：

(45)

4临坡双层粘土地基极限承载力上限解

根据上限定理，对于一个允许的机动速度场，外力做功功率与内能耗散率必然相等，在所有与任意机动允许的速度场相对应的极限荷载中，真正的极限荷载最小[17-19].根据前面确定的临坡条形基础双层粘土地基破坏模式和机动允许速度场，利用上限分析方法可确定极限承载力上限解.

WSBDE)/bV1sinβ1

(46)

根据上限定理，最优的上限解应是滑动地基处于极限状态时，临坡地基极限承载力Qu上限解的最小值，即式(46)的最小值，利用Matlab的符号运算功能编程计算可以得到临坡条形基础双层粘土地基极限承载力的目标函数表达式，于是，利用上限法求解临坡地基极限承载力可转化为非线性优化问题：

Qu=f(αi,βi)

(47)

在对上式进行优化求解时，须满足式(16)～(19)非线性约束条件，由于序列二次规划算法(SQP算法)非常适应于高度非线性问题，且具有较高的效率，因此，本文采用SQP优化算法[15]，在Matlab环境下编制相应程序，对该问题进行优化求解.

5验证与比较

5.1理论计算与有限元分析对比

为了验证本文临坡地基双层粘土地基极限承载力上限分析解法的可行性，结合工程算例采用有限元分析软件Abaqus进行临坡地基极限承载力模拟分析并与本文方法分析结果进行对比.某临坡条形基础双层地基，基础埋深H=1 m，地基持力层范围内为两层饱和粘土，第1层粘土厚度h=1.0 m，c1=40 kPa，γ1=18 kN/m3，φ1=0°，第2层粘土c2=20 kPa，γ2=16 kN/m3，φ2=0°.基础宽度b=2 m，基础外侧边缘距坡顶距离与基础宽度之比a=1，边坡坡角η=20°.

本次数值分析按平面应变问题模拟临坡双层粘土地基，条形基础为刚性基础，临坡地基材料的弹性模量E=45×103kPa，泊松比υ=0.3，土体采用弹塑性本构模型，服从线性Mohr-Coulomb屈服准则.有限元分析得到荷载-位移(P-S)曲线如图4所示，荷载加至Qu=123.5 kPa时，临坡地基滑动破坏，其相应位移场如图5所示.

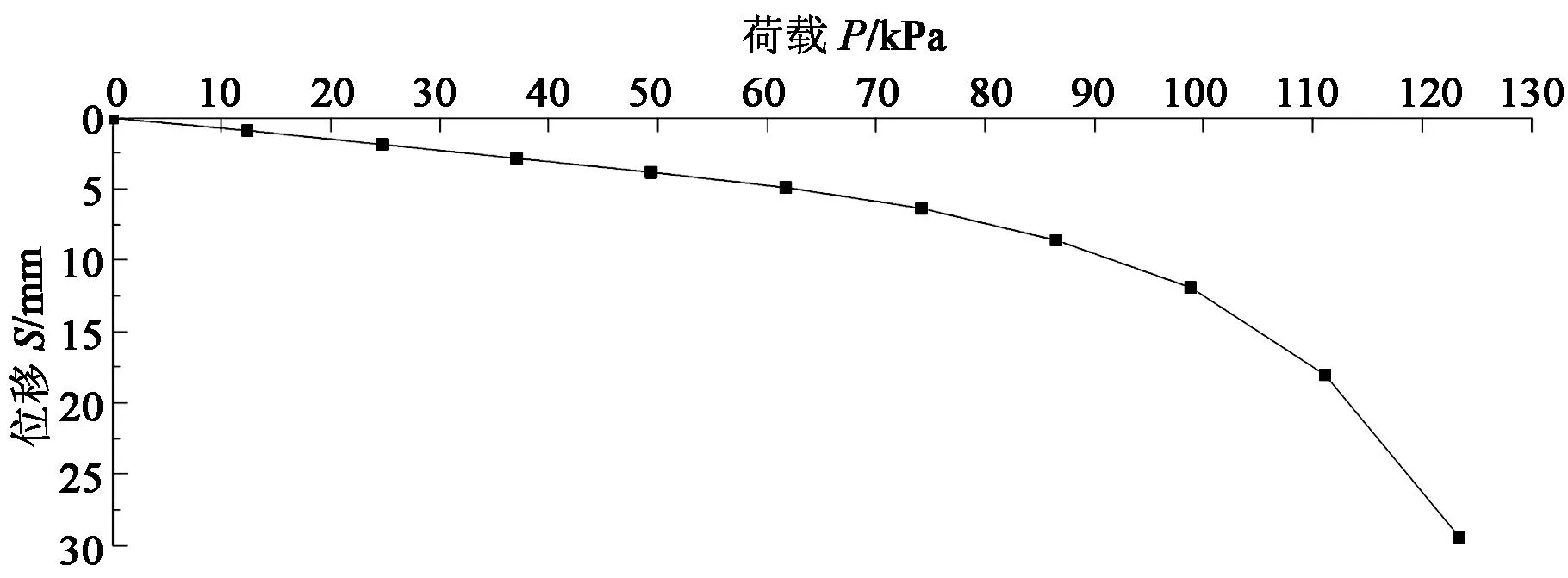
图4　临坡双层粘土地基P-S曲线

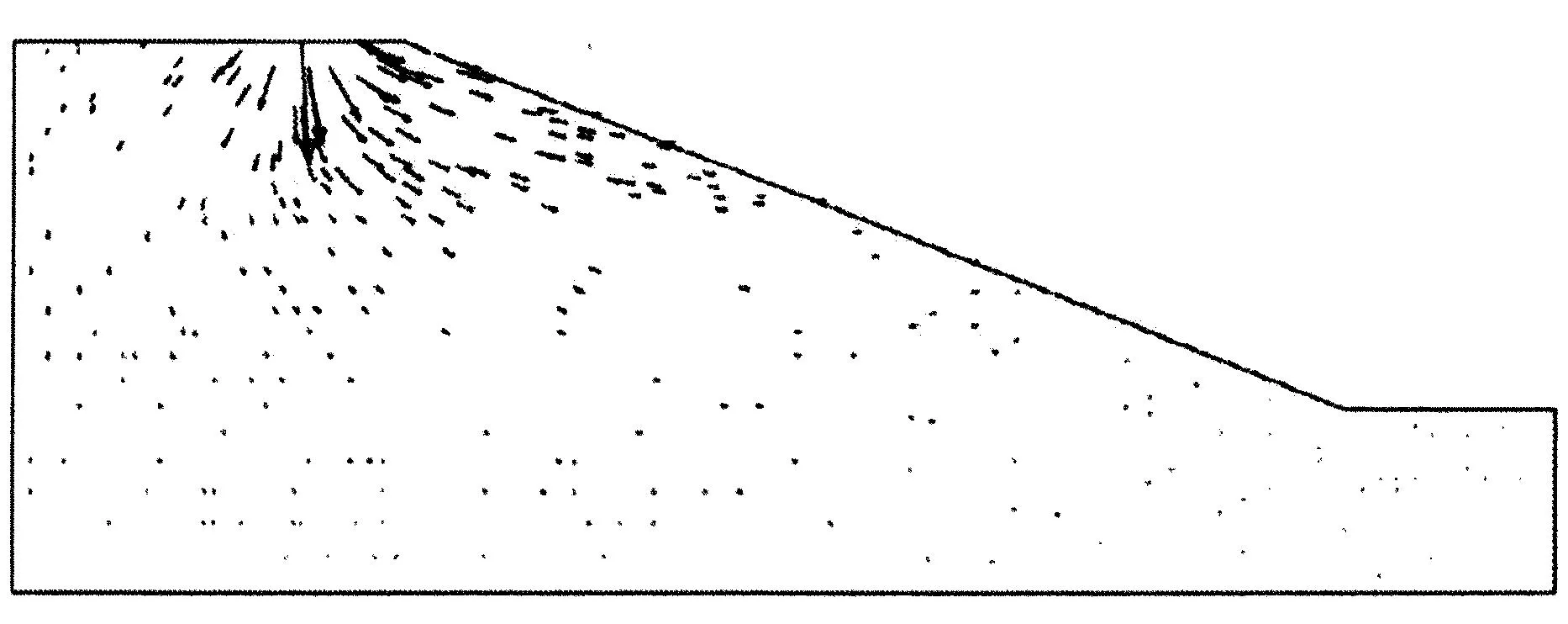
图5　临坡双层粘土地基位移场

本文采用多滑块组合分析模型，一般来说块体划分越小，刚性滑块的数量越多，结果越接近于真实解，取20个滑块时能够获得较好的上限解.根据本文方法计算该临坡条形基础双层粘性地基工程算例，得到临坡地基极限承载力Qu=128.6kPa，结果表明本文方法计算结果与有限元数值分析结果相差较小，本文上限解是较好的上限解，验证了本文上限分析方法的可行性与适用性.同时绘制本文分析方法对应极限状态下的破坏模式如图6所示，与数值模拟分析所得潜在滑裂面接近，说明了本文临坡双层地基多滑块组合破坏模型的有效性.

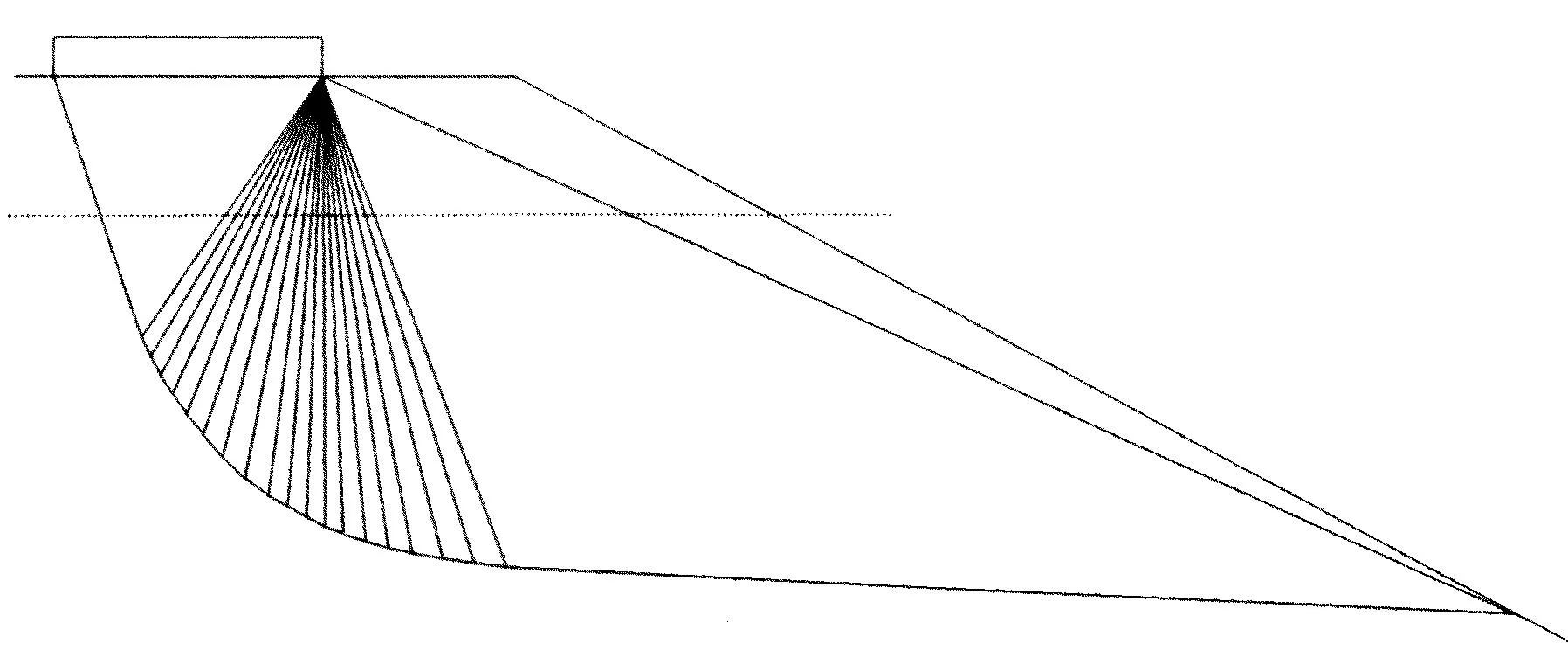
图6　优化后的破坏模式

5.2理论计算与其他上限方法的对比

为了进一步验证本文承载力公式和优化算法的正确性与优越性，采用以下算例，上下粘土层参数取相同值，研究问题变为单层土的临坡地基承载力问题，与同样采用单侧滑移破坏模式，引入上限极限理论计算临坡地基极限承载力的文献[13-15]进行比较.某临坡条形基础地基，基础宽度b=2 m，基础距坡顶距离与基础宽度比a=0，基础埋深H=2 m，地基土体重度γ=18 kN/m3，土体内摩擦角φ=30°，地基土粘聚力c=20 kPa，边坡角η=20°.计算得到临坡条形基础地基极限承载力Qu，并与文献[13-15]的计算结果进行比较分析，如表1所示.

表1　计算结果比较(距离比a=0)

本文与以上3种文献都利用了上限极限分析理论和优化方法对临坡地基极限承载力进行求解，通过比较计算结果可以看出：本文计算所得的地基极限承载力Qu数值略小,是较优的上限解，在工程实际应用中偏于安全；同时几种方法的结果较接近，这也进一步说明了本文承载力公式和优化算法的正确性和合理性.

6结论

1)本文从临坡地基出发，结合临坡成层土地基临近边坡的非对称性特征和层状地基特征，开展临坡条形基础双层粘土地基承载力性状的研究，构建了临坡地基多滑块组合单侧滑移破坏模式，为临坡成层土地基承载力确定奠定了坚实的理论基础.

2)在临坡条形基础双层粘土地基多滑块破坏模式的基础上构建对应机动允许速度场，引入上限极限分析理论和优化方法建立了可考虑地基破坏模式非对称性、地基土成层性状、基础埋深和基础与坡顶距离等影响的临坡地基极限承载力的确定方法.

3)结合工程算例，通过与有限元数值分析方法及其他上限极限分析方法的对比分析，验证了本文临坡双层粘土地基极限承载力上限解是较好的上限解，其滑动破坏面接近数值模拟潜在滑动面，表明本文方法的可行性与合理性.

参考文献

[1]HANSEN J B. A revised and extended formula for bearing capacity[J]．Bulletin of the Danish Geo-Technical Institute,1970(28):5-11.

[3]HANNA A M,MEYERHOF G G.Design charts for ultimate bearing capacity of foundations on sand overlying soft clay[J].Canadian Geotechnical Journal, 1980,17(2): 300-303.

[4]杨永新,高建红,高建明,等.双层地基极限承载力的数值分析[J].包头钢铁学院学报,2003,22(2):181-185.

YANG Yong-xin, GAO Jian-hong, GAO Jian-ming,etal.Numerical analysis about the ultimate bearing capacity of two-layer foundation[J].Journal of Baotou University of Ironand Steel Technology, 2003, 22(2):181-185.(In Chinese)

[5]GOURVENCE S, RANDOLPH M.Effect of strength non-homogeneity on the shape of failure envelopes for combined loading of strip and circular foundations on clay[J]．Geotechnique,2003,53(6):575-586.

[6]BURD H J,FRYDMAN S.Bearing capacity of plane-strain footings on layered soils[J].Canadian Geotechnical Journal,1997,34(2):241-253.

[7]FLORKIEWICZ A.Upper bound to bearing capacity of layered soils[J].Canadian Geotechnical Journal,1989,26(4):730-736.

[8]MICHALOWSKI R L,SHI L.Bearing capacity of footings over two-layer foundation soils[J].Journal of Geotechnical Engineering, ASCE,1995,121(5):421-428.

[9]MERIFIELD R S，SLOAN S W，YU H S．Rigorous solutions for the bearing capacity of two layered clay soils[J].Geotechnique,1999,49(4):471-490.

[10]CHEN W F.Limit analysis and soil plasticity[M]. Amsterdam:Elsevier,1975:170-175.

[11]秦会来，黄茂松.双层地基极限承载力的极限分析上限法[J].岩土工程学报, 2008,30(4):611-616.

QIN Hui-lai, HUANG Mao-song.Upper-bound method for calculating bearing capacity of strip footings on two-layer soils[J].Chinese Journal of Geotechnical Engineering, 2008,30(4):611-616. (In Chinese)

[12]陈昌富,曹虹,王纯子,等.下卧倾斜硬层对非均布荷载下地基沉降的影响[J].湖南大学学报:自然科学版,2014,41(6):77-84.

CHEN Chang-fu,CAO Hong,WANG Chun-zi,etal. Influnence of inclined bedrock on subgrade settlements under non-uniformly distributed load [J].Journal of Hunan University:Natural Sciences, 2014,41(6):77-84. (In Chinese)

[13]胡卫东,曹文贵.基于非对称破坏模式的临坡地基承载力上限极限分析方法[J].中国公路学报,2014,27(6):1-9.

HU Wei-dong,CAO Wen-gui.Upper limit analysis method for ultimate bearing capacity of ground foundation adjacent to slope based on asymmetry failure mode[J].China Journal of Highway and Transport, 2014,27(6):1-9. (In Chinese)

[14]赵炼恒,罗强.临坡条形基础极限承载力上限计算[J].武汉理工大学学报,2010,34(1):84-87.

ZHAO Lian-heng, LUO Qiang.Bearing capacity of strip footing adjacent to slope with upper bound theorem[J]. Journal of Wuhan University of Technology, 2010,34(1): 84-87. (In Chinese)

[15]杨峰,阳军生,张学民,等.斜坡地基单侧滑移破坏模式及承载力上限解[J].工程力学,2010, 27(6):162-168.

YANG Feng, YANG Jun-sheng, ZHANG Xue-min,etal.One-side slip failure mechanism and upper bound solution for bearing capacity of foundation on slope[J]. Engineering Mechanics,2010, 27(6): 162-168. (In Chinese)

[16]SOUBRA A H.Upper-bound solutions for bearing capacity of foundations[J]. Journal of Geotechnical and Geoenvironmental Engineering,ASCE,1999,125(1):59-68.

[17]秦会来,黄茂松,李峰.双层粘土地基极限承载力的多块体上限解[J].建筑科学,2012,28(9):40-43.

QIN Hui-lai,HUANG Mao-song,LI Feng.Muti-block upper bound solutions for the two-layer clay foundations[J].Building Science,2012,28(9):40-43. (In Chinese)

[18]陈飞,练继建,王海军.浅埋圆形基础竖向地基承载力极限分析上限解[J].湖南大学学报:自然科学版,2014,41(6):92-98.

CHEN Fei,LIAN Ji-jian,WANG Hai-jun.Upper-bound limit analysis of the vertical bearing capacity of circular shallow foundations[J].Journal of Hunan University:Natural Sciences, 2014,41(6):92-98. (In Chinese)

[19]陈祖煜.土力学经典问题的极限分析上、下限解[J].岩土工程学报,2002,24(1):1-11.

CHEN Zu-yu.Limit analysis for the classic problems of soil mechanics[J]. Chinese Journal of Geotechnical Engineering,2002, 24(1):1-11. (In Chinese)

Upper Bound Solution for Ultimate Bearing Capacity of the Two-layer Clay Foundation Adjacent to Slope

HU Wei-dong1, 2†，CAO Wen-gui1，YUAN Qing-song1

(1.Geotechnical Engineering Institute, Hunan Univ, Changsha，Hunan410082, China;2. College of Civil Engineering and Architecture,Hunan Institute of Science and Technology , Yueyang,Hunan414000, China)

Abstract:Combined with the characteristics of the asymmetry failure mode of the two-layer clay foundation near slope and layered properties, the unilateral sliding failure mode of two-layer foundation under strip footing adjacent to slope was built on the basis of the existing relevant researches. The failure mechanism was formed by many sliders. According to speed compatible relationships and triangle closed condition, the corresponding planar kinematically admissible velocity field was constructed. By introducing the upper limit analysis theory, the ultimate bearing capacity calculation model of strip footings over two-layer foundation soil was derived. A new approach for determining the ultimate bearing capacity of two-layer foundation under strip footing adjacent to slope was put forward by using sequential quadratic programming optimization algorithm. By the use of Matlab symbolic operation function and optimization function, the finite element numerical analysis results were analyzed and compared with programmed calculation. The feasibility and rationality of the proposed approach was shown.

Key words:ground foundation adjacent to slope; two-layer soils; upper limit analysis; strip footing; ultimate bearing capacity

中图分类号：U416.14

文献标识码：A

作者简介：胡卫东(1976-)，男，湖南岳阳人，湖南理工学院副教授，湖南大学博士研究生†通讯联系人，E-mail:huweidong506@163.com

*收稿日期：2014-12-24基金项目：国家自然科学基金资助项目(51378198)，National Natural Science Foundation of China(51378198)；高等学校博士学科点专项科研基金资助项目(20130161110017)

文章编号：1674-2974(2016)01-0110-07