球体直观图的尺规画法暨球直观图北极点位置定理

唐文虎

[摘 要]本文指出了流行国内的教科书中有关球体直观图画法中的错误并提出了球体直观图的正确画法以及简捷画法，同时给出了球直观图北极点位置定理的证明。

[关键词]T投影方向 轴向伸缩系数 北极点位置 尺规画法 简捷画法

中图分类号：TP391.41 文献标识码：A 文章编号：1009-914X（2016）05-0347-02

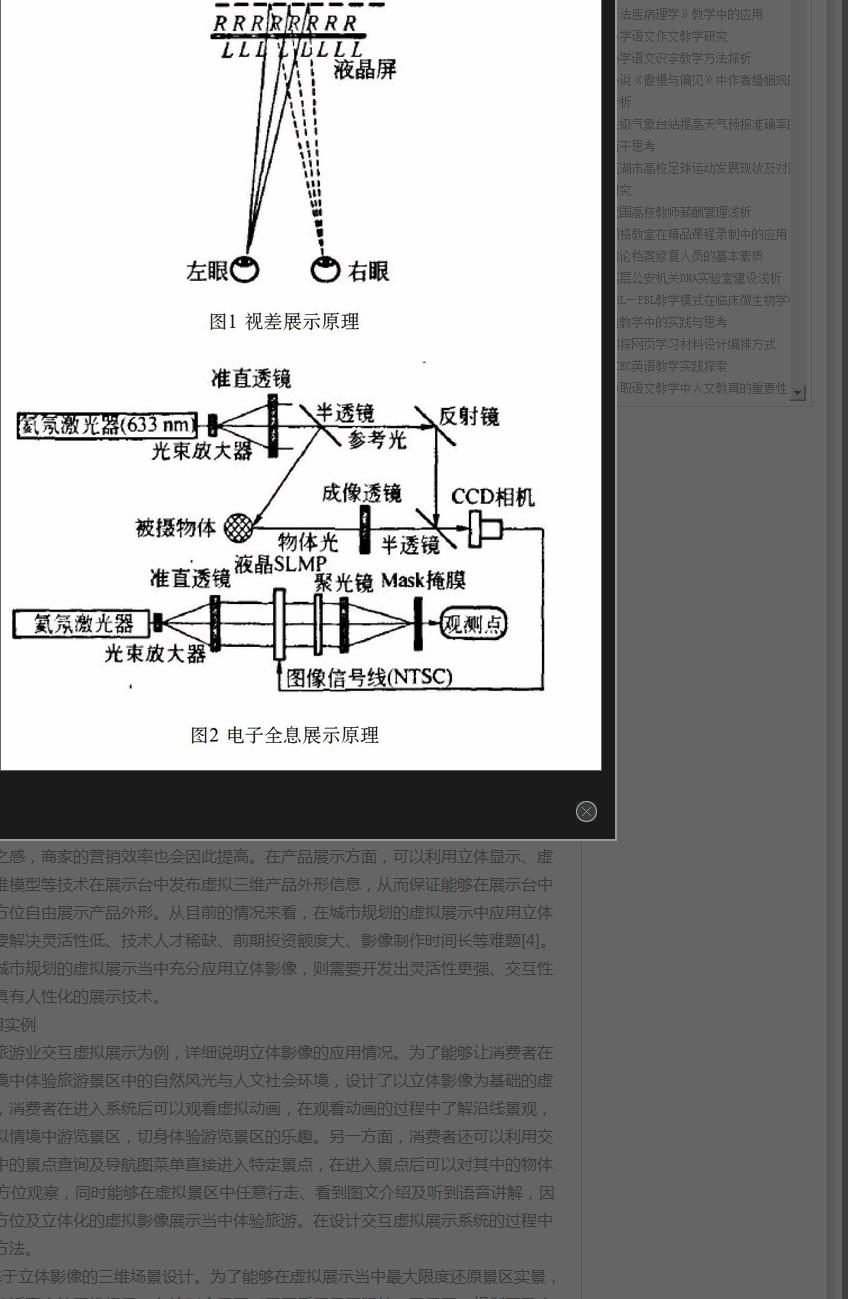
现状：目前流行国内的教科书中有关球体直观图的画法，普遍存在着严重的失误，最为典型的如图1[1]、图2[2]所示. 此类图的长期存在，其背后有着深刻的内在原因.

球体是指以半圆的直径所在的直线为旋转轴，半圆旋转一周所形成的几何体，诚然为了图形具有立体感，把赤道平面画成椭圆可以理解. 但正是这一点被无限制的重复，成为以后球直观图画法的严重障碍.

其实，按球体的定义，画出来的球体直观图赤道平面看上去应该是一条直线段，北极点在最上面，为了增加立体感，把赤道平面画成椭圆时，北极点应当有一个下移量. 由于当时下移量难以确定，就造成了目前的局面，就当时来说，问题并不显得如何严重，但发展到后来，居然成为画球直观图的严重障碍.

问题出在哪儿？

1，北极点的位置不正确.其实，北极点的位置与赤道椭圆的形状密切相关，它随着赤道椭圆离心率的变小而下移，如图3所示.

2， 轴测图关于“投影线与三个坐标平面都不平行”的规定，约束了我们的想象力，排除了原始的直接观察的方向.

为了说明问题，我们先回顾一下一些基本概念.

直 观：由汉字词义，直观，就是直接观察物体对象.

直观图：在二维平面上，画出的具有立体感的图形，叫直观图.

斜二轴测图的形成：选择一个适当的斜平行投影方向，可以得到斜二测直观图，. 可以看到，我们得到的斜二测直观图实际上是一个物体的斜影，因此，斜二测直观图不是直观的直观图.

轴测投影是平行投影的一种.将物体放在“三个座标轴和投影线都不平行的”位置，使它的三个坐标面在一个投影上都能看到，从而具有立体感，称为“轴测投影”.这样绘出的图形，称为“轴测图”.轴测投影中投射线与投影面垂直的称为“正轴测投影”.

假定我们的视线是平行的，并且视线的方向顺着平行投影的方向，这时我们看到的投影实际上是几何体的正投影. 常见的正等测直观图就是这种正投影，这种直观图就是直观的直观图. 但是，由于轴测投影要求投影线与三个坐标平面都不平行，这种规定，约束了我们的想象力，使得最原始的直接观察的方向被排除在外.

其实，有一种平行投影方向虽然不满足轴测投影方向的要求，却是最原始的直观方向：

T平行投影方向：设平行投影线与x轴、y轴、z轴的夹角依次为， 90°， 90°-a（a为锐角），则称这种投影方向为T平行投影方向.

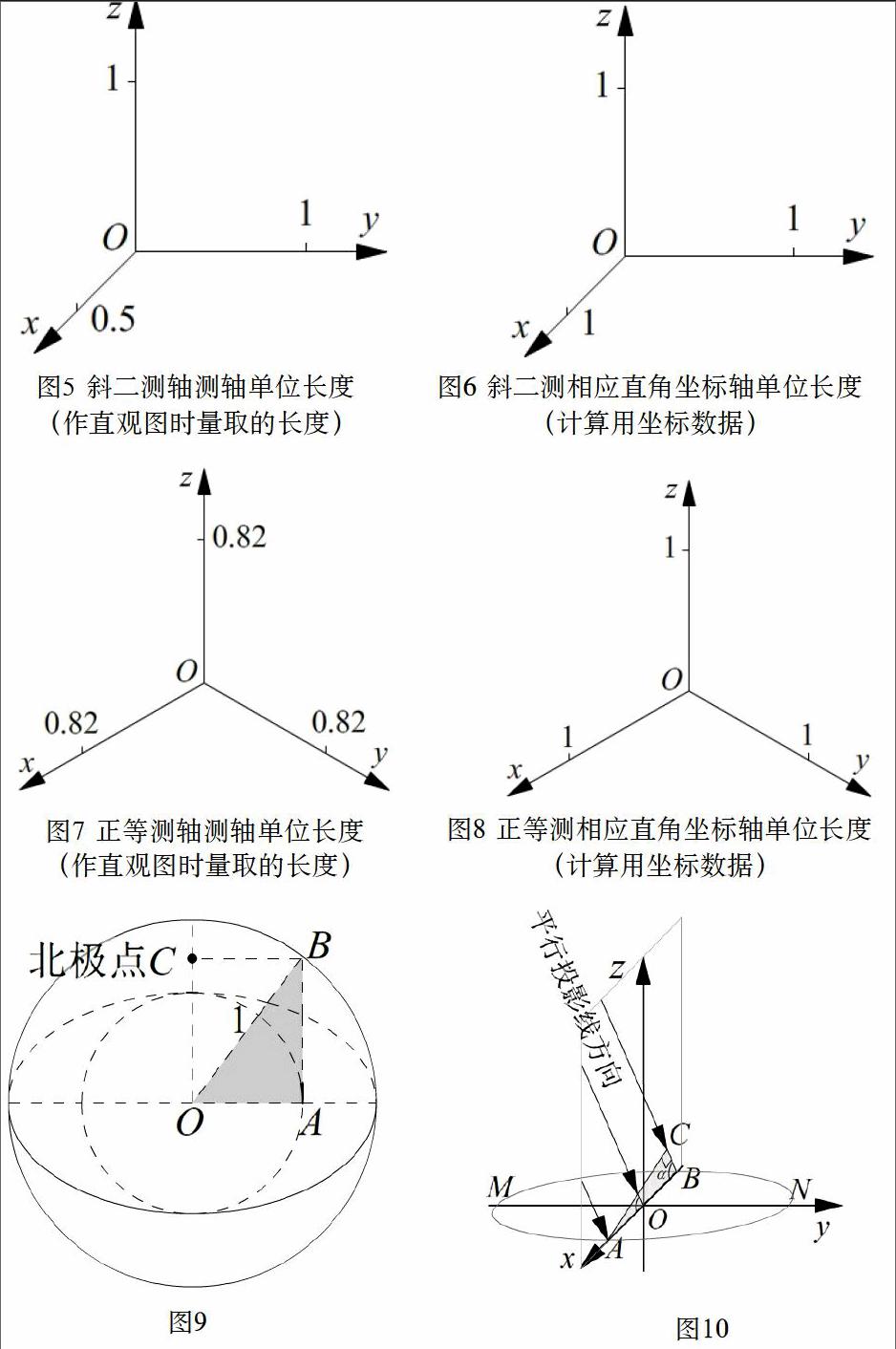
轴向伸缩系数：轴测轴的单位长度与相应直角坐标轴的单位长度的比值，叫做轴向伸缩系数. 图8～图11展示了轴向伸缩系数的意义.

不难验证下列结论.

结论一：直观图上轴测轴方向的线段长度（作直观图时量取的长度）与实际长度的比值叫做轴向伸缩系数.

结论二：在正投影时，直观图上轴测轴方向的线段长度也就是我们直接看到的、投影面上的线段长度. 所以x轴的轴向伸缩系数=AC/AB=sin？.（AC就是AB在平行投影线法平面上的射影，而AB正是在相应直角坐标系中占有的计算长度）

结论三：在T平行投影方向下，这三个座标轴的伸缩系数依次为sin、 sin90°、 sin（90°-a），即sin，1，cos.

从轴向伸缩系数的定义及其得出的结论可以看出，画直观图时轴向的线段长度可由轴向伸缩系数确定. 在正投影时，这个长度既是画图的线段长度，也是眼睛看到的（假设视线与平行投影方向一致）、因而也是直观的、在投影面上的那一部分影像. 因此，几何体在视线法平面上的射影就是几何体的直观图.

球体直观图北极点的位置定理

在T平行投影方向下，设球的半径为1，以球心O为圆心，赤道椭圆的半短轴为半径画圆，交赤道椭圆长轴于点A，过点A作椭圆长轴的垂线交球轮廓圆于点B，过点B作AO的平行线，与球体南北极所在的直线得到交点C，点C就是球体直观图的北极点，如图9所示.

用同样的方法，可以找到南极点的位置.

证明：

在T平行投影方向下，图10中的椭圆，在xOy平面中是一个圆. 所以在二维平面上画球的直观图时，赤道椭圆的短、长轴之比，就是x轴的轴向伸缩系数（见图11）.

下设球半径为1， 平行投影线与x轴、y轴、z轴的夹角依次为a， 90°， 90°-a（为锐角）.

如图12，以O为圆心，OB为半径画圆交ON于点A1， 过点A1作ON的垂线交球轮廓大圆于点B1，过点B1作ON的平行线交z轴于点C.

由结论三，cos？就是z轴的轴向伸缩系数，因此，点C就是北极点. 证毕.

球体直观图的尺规作法

已知椭圆的长轴和短轴，可由同心圆法或四心法作出椭圆.因此，在以下的作法中，一旦椭圆的长轴和短轴被作出，就认为该椭圆能用尺规作出.

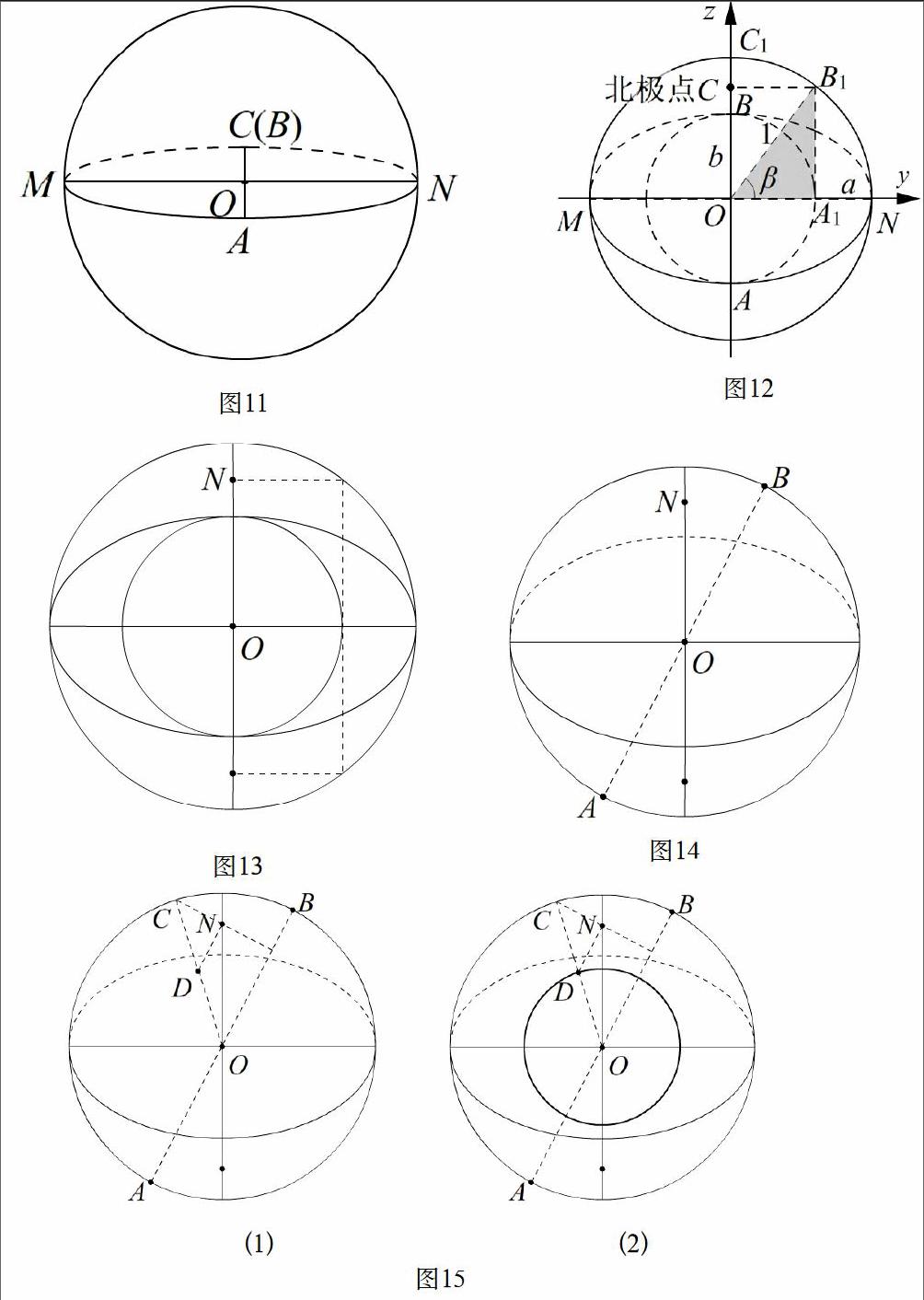
一、根据赤道椭圆，确定北极点N以及南极点，如图13所示.

二、作过极点的经线大圆

1，过球心作任意经线大圆的长轴AB，见图14；

2，经线过南北极，逆向操作找出经线椭圆半短轴长度，如图15（1），过北极点N作长轴AB的垂线交球轮廓于点C；连接OC，过北极点N作长轴的平行线交OC于点D，OD就是所求椭圆的半短轴，见图15（2）.

确定了椭圆的长轴和短轴，便可用尺规作出该椭圆，如图16.

类似地，可以作出过两极点的其它经线大圆，效果如图17所示.

四、作过极点的纬线定位大圆

南北极之间的距离就是纬线定位大圆的短轴，故可画出纬线定位大圆，如图18.

五、作平行于赤道大圆的纬线小圆

平行于赤道大圆的纬线小圆与赤道大圆具有相同的离心率，所以纬线小圆与赤道大圆的短轴、长轴之比相等. 根据纬线定位大圆确定纬线小圆的长轴PQ，再根据比例作图作出纬线小圆的短轴. 求出了纬线小圆的长轴和短轴，可由同心圆法或四心画法画出纬线小圆.

结束语

支撑球体直观图尺规画法的核心依据是“T平行投影方向”和“球体直观图北极点的位置定理”. T平行投影方向摆脱了传统轴测图思维的束搏，回归到直接观察的原始方向，从而为找到北极点位置扫清了障碍.

后记

上面虽然从理论上阐述了球体直观图尺规画法的可行性，但实际操作很麻烦. 根据上述原理，我们可以设计两块模板，达到非常方便地画出球体直观图的目的. 该模板可提供常用的若干种赤道椭圆，由“球体直观图北极点的位置定理”，找到南、北极点，然后用经线模板作出需要的经线大圆；另外，作出纬线定位大圆后，再用纬线模板画出需要的纬线小圆. 使用在“球体直观图的尺规划法”原理基础上设计的球体直观图模板画出的球体直观图效果. 我们希望它能在修正教材相关内容中起到些许作用.