电磁波极化的图形化复数教学研究

谢宝昌

(上海交通大学 电子信息与电气工程学院， 上海， 200240)



电磁波极化的图形化复数教学研究

谢宝昌

(上海交通大学 电子信息与电气工程学院， 上海， 200240)

摘要：本文利用电磁波的基本特性，将空间任意方向传播的电磁波变换到沿Z轴正方向传播的形式，然后采用矢量空间和复平面重合的形式来描述电场强度矢量合成，从而将电磁波的极化问题转换成正、反转复数的分析，利用图形直观地展现电磁波的极化规律，实践表明，图形化复数教学方法有助于学生理解电磁波的极化，也为“电机学”课程空间磁势分析方法打下基础。

关键词：电磁波; 极化; 图形化; 复空间

0引言

电磁波的极化是“电磁场”课程的重要内容之一，极化是指空间固定点电磁波场强矢量端点的运动规律，它取决于场源的性质，与发射天线有关，同时影响接收天线的方向。电磁波的极化分为线极化、圆极化和椭圆极化，其中圆极化与椭圆极化又有左旋和右旋之分。如何在教学过程中，既强调基本概念，又能直观地反映极化方式，同时充分利用学生已经掌握的知识，是课堂教学的关键。教材通常采用的场强矢端轨迹解析表达法难以达到上述要求[1-4]。

本文针对场强矢量只有垂直于传播方向的两个分量的特点，采用复平面表达场强矢量端点轨迹，用图形化形式形象而直观地展现电磁波的极化方式，解决此问题。该图形化教学方法也为电气工程专业“电机学”课程空间磁势波形分析打下基础。

1电场强度的一般表达式

均匀平面电磁波的特点是波矢量、电场强度矢量和磁场强度矢量相互正交，而且满足右手螺旋关系。因此只要分析电场强度的极化方式，磁场强度具有类似的结论。

本文用粗体表示矢量，考虑一般形式的均匀平面电磁波，令θ=ωt-k·r，电场强度矢量表示为

E=axEmxcos(θ+φx)+

ayEmycos(θ+φy)+azEmzcos(θ+φz)

(1)

其中，ω为角频率，波矢量k=axkx+ayky+azkz，ak为波矢量的单位矢量，r为空间位置矢径，E的各分量幅值Emx，Emy和Emz不等于零，初始相位分别为φx，φy和φz。波矢量与电场强度矢量满足正交约束关系

k·E=0

(2)

2空间坐标变换

由式(1)和(2)可以简化电场强度矢量

E=A1cos(θ+φx)+A2cos(θ+φy)

(3)

其中，矢量A1和A2分别以各自的单位矢量和模的积表示。

(4)

式(4)中矢量A1和A2既不重合也不垂直，但它们都与波矢量垂直，两矢量夹角β满足

a1·a2=cosβ

(5)

a1×a2=cosksinβ

(6)

如图1所示，将空间直角坐标系xyz变换为XYZ，使得Z轴正方向与波矢量方向一致，三个坐标轴单位矢量分别为

ax=a1，ay=ak×a1，aZ=ak

(7)

由式(4)和图1可得，单位矢量a1位于zox平面且与波矢量k及其zox平面上的投影矢量kzx=axkx+azkz垂直。单位矢量a2位于yoz平面且与k及其yoz平面上的投影矢量kyz=ayky+azkz垂直。

3复平面内电场强度矢量的图形描述

为了简便起见，利用标量积不变性k·r=kZ，令θ=ωt-kZ，将式(4)代入式(3)后得到

E=a1A1cos(θ+φx)+a2A2cos(θ+φy)

(8)

式(8)表明电场强度在XYZ坐标系中只有两个分量，分别沿单位矢量a1和a2变化且幅值分别为A1和A2，电场强度矢量端点轨迹是这两个分量的合成。

现以X轴为实轴，Y轴为虚轴建立复平面，单

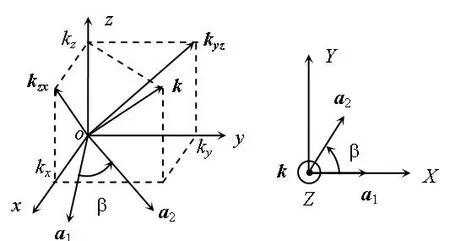
(a) xyz坐标系　　　 (b) XYZ坐标系图1　波矢量与电场强度分量单位矢量

位矢量a1和a2的复数形式分别为1和ejβ，由式(5)得到β=cos-1(a1·a2)，电场强度表示为复数形式

E=A1cos(θ+φx)+ejβA2cos(θ+φy)

(9)

式(9)是电场强度矢量在复平面中的形式，与电磁场理论中时谐场复数形式是完全不同的[1-4]。

利用欧拉公式将正弦量表示为复数形式

2cos(θ+φ)=ej(θ+φ)+e-j(θ+φ)

(10)

式(10)表明一个正弦量可以看成是两个共轭复数之和，由于角度θ是随时间增长而增大的，因此这两个共轭复数在复平面上是旋转的，旋转角速度等于时间变化角频率ω，这里的φ表示φx或φy。

式(9)中电场强度的a1分量用式(10)表示为

(11)

式(11)表明沿X轴随时间变化的正弦波可以表示为以X轴为对称轴的两个旋转分量E1p、E1n之和，它们的幅值相等但大小等于正弦波幅值一半，旋转角速度都等于时间角频率而转向相反的复数表示，如图2(a)所示。

类似地，式(9)中电场强度的a2分量表示为

(12)

式(12)表明沿单位矢量a2方向随时间变化的正弦量可以表示为以a2为对称轴的两个旋转分量E2p、E2n之和，它们的幅值相等但大小等于正弦波幅值一半、旋转角速度都等于时间角频率而转向相反，如图2(b)所示。

图2表明，一个线极化波由两个幅值和转速相同但转向相反的圆极化波合成，线极化波矢量位置是这两个圆极化波矢量的对称轴。

复平面内电场强度有两个逆时针正向旋转的分量E1p和E2p，以及两个顺时针反向旋转的分量E1n

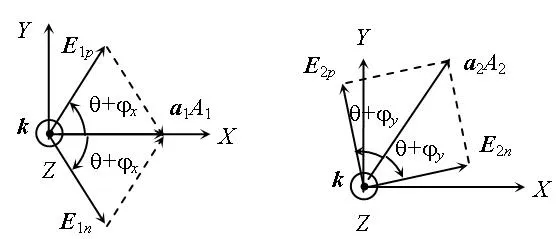
(a) a1分量旋转复数表示 (b) a2分量旋转复数表示

和E2n，它们分别合成正向和反向旋转分量，如图3所示。合成后，电场强度正反转复数形式分别为

(13)

(14)

4电磁波的极化方式

由几何图形可以知道，复平面上两个旋转角速度相同而旋转方向相反的复数合成是椭圆，但当两个复数的幅值相同时，椭圆退化为直线段，当其中一个复数的模等于零时，椭圆变为圆。

4.1复数模相同

如图4所示，两个复数的模相同，那么可以得到

sin(φy-φx)=0

(15)

解得φy-φx=nπ，其中n为整数。这表明式(8)是两个相位相同或相反的线极化波合成，于是得到

E=[a1A1+(-1)na2A2]cos(θ+φx)

(16)

式(16)表明电场强度矢量是方向固定而大小随时间正弦规律变化的线极化波。两个相位相同或相反的线极化波合成一个线极化波。

4.2复数模乘积等于零

若Ep=0，由式(13)得φy-φx+β=(2n-1)π且A1=A2，电场强度只有反转复数，代入式(14)可得E=En=A2e-j(θ+φx-β-π/2)sin(φx-φy)

(17)

图3　正、反转复数 　　图4 复数模相同的线极化波

反转复数的模恒定，因此空间固定点的电场强度矢量端点轨迹在复平面上随时间变化是顺时针旋转的圆，电磁波是左旋圆极化波，如图5(a)所示。

若En=0，由式(14)得φy-φx-β=(2n-1)π且A1=A2，电场强度只有正转复数，代入式(13)可得

E=Ep=A2ej(θ+φx+β-π/2)sin(φx-φy)

(18)

电场强度矢量端点轨迹在复平面上是逆时针旋转的圆，电磁波是右旋圆极化波，如图5(b)所示。

(a) 反转左旋圆极化波 (b) 正转右旋圆极化波图5　复数模乘积为零的电磁波圆极化

4.3复数模不同且不等于零

将式(13)和(14)改写为模和复角形式，再合成电场强度矢量得到

E=Ep+En=Apej(θ+φx+φp)+Ane-j(θ+φx+φn)

(19)

当2(θ+φx)+φp+φn=2nπ时，两个复数旋转到重合位置，电场强度最强，数值上等于Ap+An。

当2(θ+φx)+φp+φn=(2n-1)π时，两个复数旋转到相反方向的位置，电场强度最弱，数值上等于|Ap-An|，方向处在模大的复数位置。因此合成电场强度复数的转向取决于模大的复数转向。

令θe=θ+φx+(φp+φn)/2，将式(19)改写为

E=(Apejθe+Ane-jθe)ej(φp-φn)/2

(20)

式(20)表明场强矢端轨迹是倾角等于(φp-φn)/2的椭圆。椭圆的旋转方向取决于两个旋转复数的模。若Ap>An>0，则两个幅值不同、旋转角速度相同但转向相反的复数合成一个逆时针旋转的右旋椭圆极化波，如图6(a)所示。若An>Ap>0，则合成一个左旋椭圆极化波，如图6(b)所示。

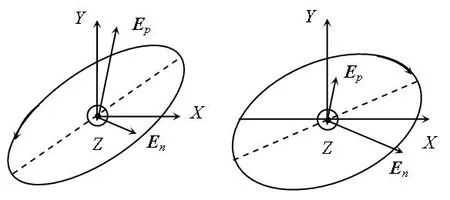
(a) 正转右旋椭圆极化波 (b) 反转左旋椭圆极化波图6　复数模非零且不同的电磁波椭圆极化

(谢宝昌文)

5结语

本文利用电磁波场矢量与传播方向正交的特性，将任意方向传播的电磁波变换到沿Z轴正方向传播的形式，使得电场强度的两个分量位于XY复平面内，从而将电磁波的极化问题转换成分析两个正、反转复数合成的矢端轨迹的问题，利用图形直观地展现电磁波的极化规律，实践表明，图形化复数教学方法有助于学生理解电磁波的极化，也为“电机学”课程空间磁势与磁场合成分析方法打下基础。

参考文献:

[1]周希朗. 电磁场. 北京：电子工业出版社，2008年

[2]谢处方，饶克谨. 电磁场与电磁波. 北京：高等教育出版社，第4版，2006年

[3]王蔷，李国定，龚克. 电磁场理论基础. 北京：清华大学出版社，2001年

[4]陈重，崔正勤，胡冰. 电磁场理论基础. 北京：北京理工大学出版社，第2版，2010年

Research on Graphic Visualization Complex Teaching of Electromagnetic Wave Polarization

XIE Bao-chang

(SchoolofElectronicInformationandElectricalEngineering,ShanghaiJiaoTongUniversity,Shanghai200240，China)

Abstract：Spatial coordinate transformation is firstly introduced to make the wave propagation align with the direction of Z-axis based on orthogonal property of field and wave vectors in this paper. Then combination of vector and complex space is adopted to describe the electric field waveform as rotating complex vectors in counterparts. Thus graphic visualization is illustrated to analyze the polarization of the electromagnetic wave, which helped students to deeply understand the concept of polarization and solidify foundation for further analyzing spatial magneto-motive force of Electric Machinery.

Keywords：electromagnetic wave; polarization; graphic visualization; complex space

文献标识码：A

文章编号：1008-0686(2016)01-0046-04

中图分类号：TM151

作者简介：谢宝昌(1965-)，男，博士，副教授，主要从事电机与电器的教学与研究工作，E-mail：bcxie@sjtu.edu.cn

收稿日期:2015-02-08;修回日期:2015-09-21