两铰拱在径向均布载荷下的稳定性研究

张应迁��

摘要：针对圆拱在径向均布载荷下的屈曲问题，在基于Boussinesq、Lamb方程求解圆拱径向临界载荷的基础上，通过采用变分法、有限单元法并经数值验证发现，BEAM3单元误差较大，并且误差随中心角的增大而增大，而BEAM188以及SHELL181单元分析结果与理论解吻合相当好。因此，可以在实际设计当中采用BEAM188或SHELL181单元进行结构临界载荷的确定。

关键词：两铰拱；变分法；有限单元法；ANSYS

中图分类号：U448.22 文献标志码：B

Abstract： In traditional method， the critical load of circular arch buckling is obtained by solving Boussinesq and Lamb equations. The variational method and finite element method were used to study the radial critical load of the circular arch. By numerical verification， the error of the BEAM3 element is large， and the error grows with the increase of the central angle. The results of BEAM188 element and SHELL181 element are in good agreement with theoretical results. Therefore， the BEAM188 element or SHELL181 element can be used to identify the critical load of the structure.

Key words： two-hinged arch； variational approach； finite element method； ANSYS

0 引 言

在竖向载荷作用下产生水平反力的曲杆结构称为拱。拱在工程中有很广泛的应用，在公路工程中拱桥是最基本的桥型之一。

拱与梁不仅是外观不同，更重要的是在竖向载荷作用下产生水平反力，这种水平反力也称为推力。由于水平推力的存在，拱中各截面的弯矩比曲梁式简支梁的弯矩小得多，这使拱成为一种以受压为主的结构。因此，拱可以用抗压强度较高而抗拉强度低的砖、石、混凝土等材料修建，这是拱结构的主要优点。拱的缺点是支座要承受水平推力，因而要求具有比梁更为坚固的基础支撑结构[1-2]。

圆拱在径向载荷下的屈曲问题一直是众多学者研究的热点。Kirchhoff最早提出拱稳定的数学理论；Bryan第一个系统研究了拱的平衡稳定；Southwell进一步研究了弹性体的稳定性问题；Nikolaii对圆环和圆拱的稳定性做了大量的研究；还有对圆拱弹性稳定做出巨大贡献的Timoshenko。随着计算机技术的迅速发展，数值方法在圆拱稳定性研究方面起的作用越来越大，Smirnov在这方面做了大量的工作，Gaber、Dinnik、Morgaevsky等在圆拱稳定性试验验证方面进行了很多探索。本文基于Boussinesq、Lamb方程求解圆拱径向临界载荷，并将变分法和有限单元法运用到圆拱径向临界载荷的研究中。

1 圆拱径向载荷作用下的面内失稳

圆拱在径向载荷作用下的面内失稳研究主要基于2类方程，即Boussinesq方程和Lamb方程。前者研究的重点是径向位移，后者研究的重点则是切向位移。研究圆拱在径向载荷下的屈曲问题，对拱有以下3点基本假设：圆拱所采用的材料需满足线弹性（即满足胡克定律）；拱的中心线不可压缩；作用在拱上的载荷均为保守力系。

1.1 Boussinesq方程

3 有限单元法

有限单元法是一种有效解决数学问题的解题方法。其基础是变分原理和加权余量法，基本求解思想是把计算域划分为有限个互不重叠的单元，在每个单元内，选择一些合适的节点作为求解函数的插值点，将微分方程中的变量改写成由各变量或其导数的节点值与所选用的插值函数组成的线性表达式，借助于变分原理或加权余量法，将微分方程离散求解。采用不同的权函数或插值函数形式构成不同的有限元方法。有限元方法最早应用于结构力学，后来随着计算机的发展慢慢用于流体力学的数值模拟。ANSYS作为强大的有限元分析商业软件，是世界范围内增长最快的计算机辅助工程（CAE）软件，能与多数计算机辅助设计（CAD）软件接口，如Creo、NASTRAN、Alogor、I-DEAS、AutoCAD等，实现数据的共享和交换。同时，ANSYS软件也是融结构、流体、电场、磁场、声场分析于一体的大型通用有限元分析软件，在核工业、铁道、石油化工、航空航天、机械制造、能源、汽车交通、国防军工、电子、土木工程、造船、生物医学、轻工、地矿、水利、日用家电等领域有着广泛的应用。

4 数值验证

分别采用ANSYS中常用的3种单元来研究圆拱在径向载荷下的屈曲问题，即BEAM3、BEAM188、SHELL181。BEAM3单元共有3个自由度，面内的2个平动自由度以及垂直于该面的转动自由度，而BEAM188和SHELL181单元共有6个自由度，即3个平动自由度和3个转动自由度。

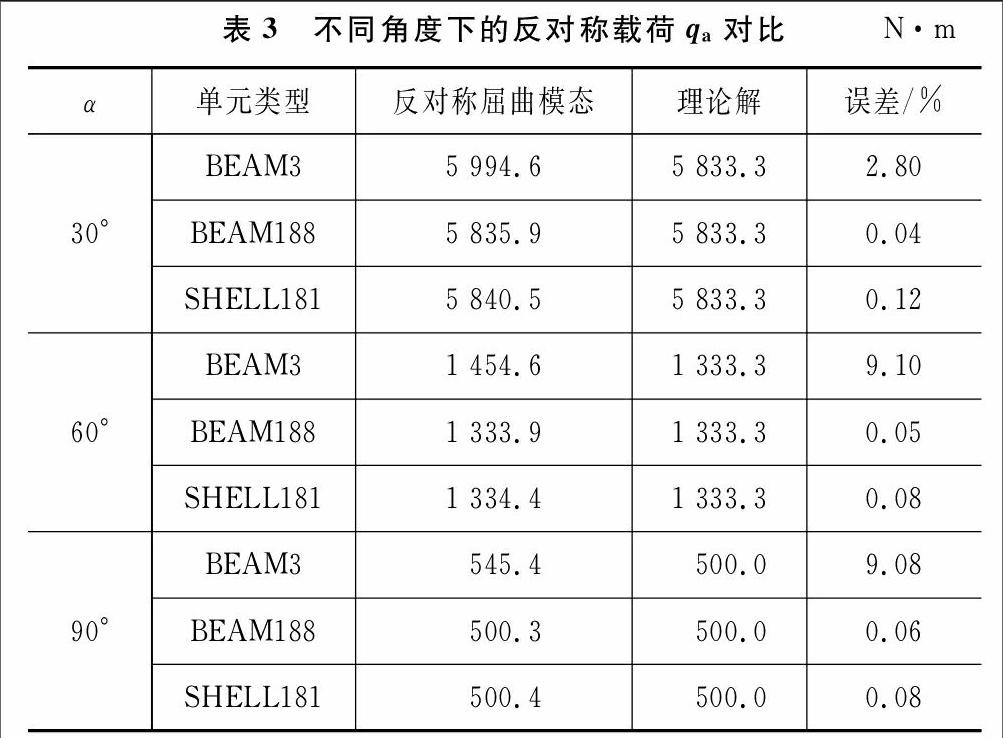
为了验证ANSYS的3种单元对圆拱屈曲载荷模拟的准确度，选用工程中常用的矩形截面b×h=001×0.01，材料为Q235钢，弹性模量为2×1011 Pa，圆拱半径R=1 m。表3、4分别列出了不同中心角α下3种单元模拟的屈曲载荷与理论解的对比，其中表3对应的是反对称模态，表4对应的是对称模态。图2～4分别对应30°、60°、90°圆拱屈曲模态，图5、6为不同有限元单元计算结果与理论解的对比。

5 结 语

在求解Boussinesq以及Lamb方程的基础上得到圆拱径向临界载荷，同时将变分法运用到圆拱径向临界载荷的研究上来。通过对比发现3种方法的结果一致，在研究过程中发现通过Lamb方程可以很容易分别得到圆拱屈曲对应的反对称和对称临界载荷，而Boussinesq方程以及变分法相对要繁琐一些。

从表3、4可以看出BEAM3单元模拟圆拱在径向载荷作用下的屈曲载荷精度相对较差，误差随着角度的增加也有所增加；而BEAM188以及SHEL-L181单元精度较高，最大误差不超过3%，能较好地满足任意角度下圆拱临界载荷的确定。从图5、6可以看出，有限元分析中不同单元计算结果虽然和理论解有所差异，但是临界载荷随中心角α的变化趋势却是一致的。

当然关于两铰圆拱在径向载荷下的屈曲问题还有许多考虑的因素，比如由于制造误差导致的截面不均匀、安装过程中出现的预应力、施工过程导致的各截面曲率半径不相等、初始缺陷、材料非线性、后屈曲等，这些都是下一步需要研究的重点内容。

参考文献：

[1] 王勖成.有限单元法[M].北京：清华大学出版社，2003.

[2] 张应迁，张洪才.ANSYS有限元分析从入门到精通[M].北京：人民邮电出版社，2010.

[责任编辑：谭忠华]