小城镇应急物资储备库等级优化配置模型与实证——以北京市房山区为例*

陆相林，苗长虹

(1. 河南大学 黄河文明与可持续发展研究中心，河南 开封 475001；2. 石家庄学院 经济管理学院，河北 石家庄 050035)



小城镇应急物资储备库等级优化配置模型与实证
——以北京市房山区为例*

陆相林1，2，苗长虹1

(1. 河南大学 黄河文明与可持续发展研究中心，河南 开封 475001；2. 石家庄学院 经济管理学院，河北 石家庄 050035)

摘要:“小城镇，大战略”背景下，加强小城镇应急管理成为一项具有重大挑战性的研究课题。针对我国小城镇应急设施选址定量分析文献较少的现实，结合小城镇应急物资储备库管理与物资调度实际，对等级设施选址理论中的最大覆盖模型加以改进，构建了考虑覆盖半径内需求满意差异性，具有单流、嵌套性、同调性特征的小城镇应急物资储备库等级选址模型，并利用蚁群算法进行求解。以北京房山区为例进行实证，以整体应急服务满意度最大为目标，实现了房山区8个区级应急物资储备库、25个乡镇级应急物资储备库的等级优化配置，并绘出配置图，给出房山区应急物资储备库优化配置的相关建议，为我国小城镇应急管理工作的科学化提供一定的决策依据。

关键词:设施选址；应急物资储备库；等级最大覆盖；小城镇；北京市房山区

设施选址问题(facility location problem，FLP)是“选址”(location)研究的核心主题之一，研究一系列设施(如应急设施、物流中心等)具体位置的选择[1]，对消防、医疗、工商业等各方面而言都极为重要[2-4]。国外有不少较经典的研究[5-8]。等级选址问题(Hierarchical location problem)是设施选址研究的一个重要领域，相关研究主要集中于模型构建、算法设计与空间决策支持三个方向，主要应用于物流规划、应急设施选址等方面[9-10]。

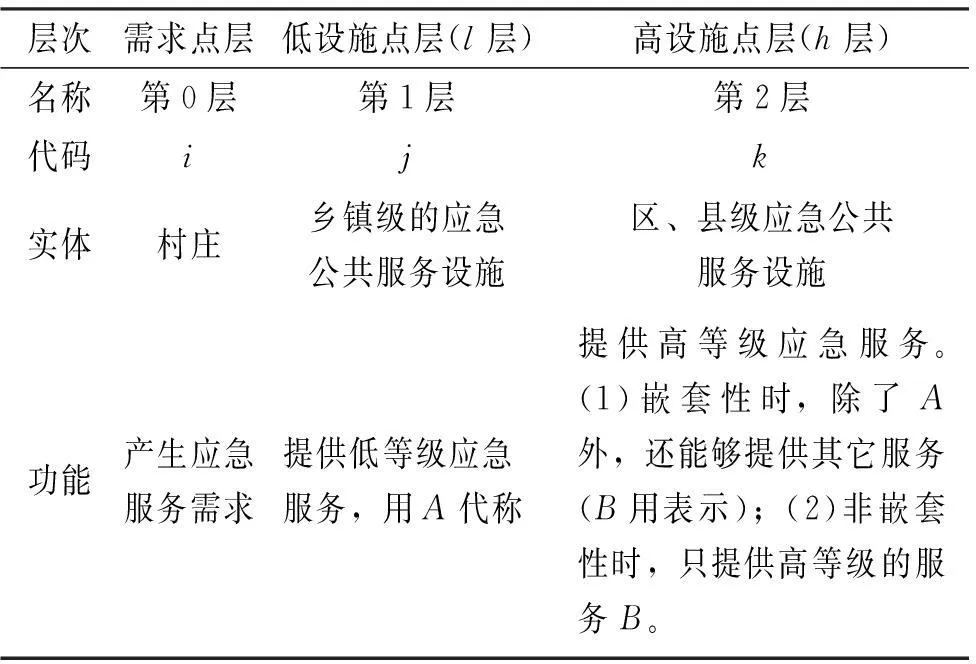
表1　小城镇应急公共服务设施系统等级结构

现实中，无论是公共还是私营设施系统，常常存在等级性，如医疗系统、物资储备、物流配送系统等。小城镇应急公共服务设施也可以分为多个等级(表1)。等级设施系统中，不同等级的设施提供不同水平的服务，设施之间可通过物流、人流、信息、资金等形式密切联系。因此，仅单独考虑某一等级的优化并不能实现整体最优。等级设施选址系统中一般有k个水平等级的设施，最低等级的设施水平为1，最高等级的设施水平为k，与之联系，学者们习惯把需求点也看作一个等级，水平定义为0。如表1所示，显示了一个2等级的小城镇应急设施系统。

学者们常常从等级选址的流(flow)模式、服务可用性(serviceavailability)、空间结构和目标四个属性维度对之进行研究：Narula[11]最早提出等级设施选址问题的单流(single-flow)和多流(multi-flow)模式；Marianov和Serra[12]根据设施的服务可用性(serviceavailability)原则，提出嵌套(nested)和非嵌套(non-nested)等级选址问题；Serra和ReVelle[13]基于设施分布的空间特征，提出等级设施选址同调性(coherent)和非同调性(non-coherent)问题；Sahin和Süral[14]从中位(median)、覆盖(covering)和固定费用(fixedcharge)三个目标角度确定等级设施选址问题的类别，并对1986年至2007年之间的等级设施选址研究成果进行分类综述。国内方面，陆相林等[15]对国内外最新设施选址理论进行了概述，在此基础上提出了考虑覆盖半径内需求满意差异的选址问题。陈志宗等[16]讨论了城市防灾减灾设施的等级选址问题及应用。

应急物资调度、储备规划与建设是应急管理研究的热点领域之一。冉岚[17]回顾了我国物资储备的历史状况，提出必须建设信息共享的储备系统，完善储备的布局。杨子健[18]提出应构建社会储备与专业储备相结合、政府储备与商业储备相结合、实物储备与生产能力和生产技术储备相结合的“三结合”储备模式。张永领[19]提出了我国应急物资储备体系完善的基本思路。定量研究中，郭子雪等[20]研究了基于梯形模糊数的应急物资储备库最小加权距离选址模型。葛春景等[21]基于轴辐理论，提出应对重大灾害的轴辐式应急物资储备网络体系构建思路。陆相林等[10]基于设施选址理论构建了覆盖半径内需求满意存在差异的最大覆盖设施选址模型，并以北京房山区为例实证。

小城镇包括小型城市、建制镇以及乡集镇[22]。“小城镇，大战略”背景下，加强我国小城镇的应急管理，构建科学的应急管理模式，具有重大现实意义[23-24]。统计表明：有效的应急系统可将事故损失降低到无应急系统的60%[25]。小城镇应急管理需要构建富有应变能力、及时畅通、科学有效的应急设施系统。北京市政府非常重视应急管理和应急物资储备库建设工作，其市一级的应急物资储备库已经建成，今后的建设重点是向街乡和社区延伸，计划两年内北京市16区县都将建成物资储备库。

综上所述，应急物资储备库相关问题的研究尚处于起步阶段，多以定性描述建设现状，提出相关对策建议为主。定量研究中对等级设施选址问题缺乏关注，较少联系国家、地区实际情况，定量探讨小城镇应急物资储备库配置合理性的文献则更少。因此，把等级设施选址理论应用于中国小城镇的应急物资储备库等级优化配置，为我国小城镇应急管理提供科学支撑极有必要。

基于上述考虑，本文将对文献[10]的研究加以拓展，综合考虑流模式、服务可用性、空间结构、目标四个维度，建立考虑覆盖半径内需求满意差异的，具有单流、单目标、嵌套式、同调性的小城镇应急物资储备库等级优化配置模型，并以北京市房山区为例进行实证。

1等级优化配置模型

小城镇应急物资储备库等级优化配置问题属于设施选址问题的范畴。设施选址问题涉及两类站点：一类为需求站点；另一类为服务站点，文章中统称为设施点。由于设施点要为需求点提供服务，因此，一般用距离或者时间来表示设施点与需求点之间的联系紧密程度，为了简化分析且不失一般性，本文仅以距离为例进行分析。

1.1假设

①假设应急物资需求和应急物资储备库以点状产生，其中应急需求点实体形态为村庄。②假设应急物资储备库存在等级性，分为两个等级，低等级定义为第1等级，称为乡镇级应急物资储备库；高等级定义为第2等级，称为区级应急物资储备库；把应急物资需求点定义为第0等级。③任意应急物资储备库与需求点的距离可通过调查或者计算得到。④由于应急物资储备库建设与维护成本较高，故个数要有限制。⑤假设每一需求点最多只能由一个应急物资储备库服务。⑥假定应急物资储备库选址于各乡镇政府机关所在地，每一乡镇都建一处乡镇级应急物资储备库，负责本乡镇辖区内的应急物资储备、调度与分配，管理权属于本乡镇，同时接受上一级的区级应急物资储备库垂直管理、协调与监督。⑦为了实现应急物资的均衡布局，假设区级应急物资储备库在区内有多个分布。⑧假设居民应急救助满意度具有距离(时间)敏感性，即距离应急设施点越近，安全感愈强，满意度愈高。⑨假设应急物资储备库等级服务可用性表现为嵌套性，即高等级应急物资储备库的服务功能更强大，除了能够提供低等级可提供的服务外，还可提供其他服务。

1.2符号定义

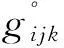
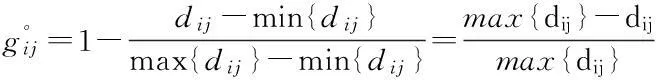
(1)

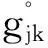
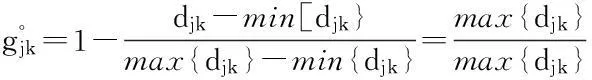
(2)

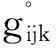
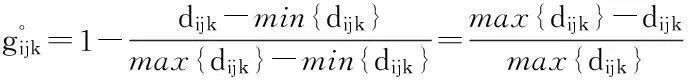
(3)

式中：xijk为需求变量，当需求点i被低等级设施j和高等级设施k服务时，取值为1，否则为0；yjk为设施配置变量，当低等级设施点j受到高等级设施点k覆盖时，取值为1，否则为0；wj为设施配置变量，低等级设点配置在j点时，取值为1，否则为0；zk为设施配置变量，高等级设施点配置在k点时，取值为1，否则为0。

1.3模型构建

依据假设，对Marianov，Serra[12]提出最大覆盖等级选址改进，构建如下模型。

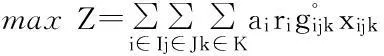
(4)

s.t

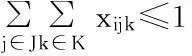
(5)

xijk≤yjk,∀i,j,k ,

(6)

yjk≤zk,∀j,k ,

(7)

yjk≤wj,∀j,k ,

(8)

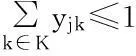
(9)

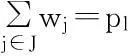
(10)

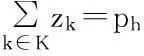
(11)

xijk,wj,zk,yjk=0,1, ∀i,j,k 。

(12)

目标函数式(4)努力实现居民应急救助整体满意度的最大化。约束条件中，式(5)实现每一应急需求点仅由一设施点覆盖；式(6)～式(8)保证应急需求点只有被一高级应急物资储备库及其下辖的低级应急物资储备库覆盖时，才能取值为1；式(9)意指某一低级应急物资储备库只能由一个高级应急物资储备库覆盖；式(10)、(11)分别保证待建设设施点数目为预定数目；式(12)为同调性约束；式(13)保证xijk,wj,zk,yjk为0-1变量。

1.4模型简化

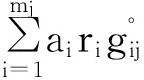
因此，原问题就转化为超级节点与第2层高级应急物资储备库的空间联系优化问题，模型简化为：

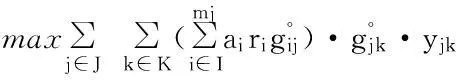
(13)

s.t

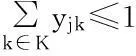
(14)

yjk≤zk,∀j,k ,

(15)

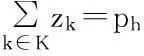
(16)

yjk,zk,=0,1, ∀j,k 。

(17)

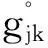
2房山区应急物资储备库等级优化配置

基于所建模型，对北京市房山区应急物资储备库进行等级优化配置。

2.1配置依据

北京市房山区位于115°25′～116°15′E、 39°30′～39°55′N ，总面积2 019 km2，是京郊大区。北京市将房山定位成未来西南的经济重心、现代农业和制造业的主要载体，中心区产业、人口的重要疏散区域。房山区突发公共事件具有种类多、成因复杂、处置难等特点[10]，应急管理任务艰巨。低温冷冻、大风、冰雹、冰雪等气象灾害以及地质灾害、地震灾害、生物灾害是房山区的主要自然灾害。安全生产事故、危险化学品事故、重特大传染病疫情、重特大动物疫情、重特大群体性事件、重大危险源事故及爆炸事故等灾害是主要的人为致灾因素。房山区专业队伍力量较弱，设备不足，应急物资储备库建设极为必要。

截止到2013年底，房山区全区常住人口101万人。共辖28个乡、镇、街道办事处，其中，街道办事处8个、建制镇14个、建制乡6个，共有124个居委会、459个村委会。然而，据房山区统计惯例，常对城关街道、拱辰街道等25个乡镇级单位进行年度统计，结合假设⑥，本文确定房山区25个乡镇级应急物资储备库个数为25。根据假设⑦，房山区一些交通、区位条件优越，经济地位突出的乡镇需要配置区级应急物资储备库。

结合《国家突发事件应对法》的要求，所建模型适用《中华人民共和国国家突发公共事件总体应急预案》中Ⅲ级(较大)和Ⅳ级(一般)突发公共事件的应对，同时本配置也会可对Ⅰ级(特别重大)、Ⅱ级(重大)突发公共事件起到协助配合作用。配置中的距离用公路行车距离表示，北京灵图软件技术有限公司致力于中国的LBS(定位信息服务)与数字城市(区域)建设，该公司的“我要地图网”网站与谷歌网站的地图功能相似，但设计上更贴合中国国情，可提供我国村级单位之间的测距，且结果较为准确。本文数据由“我要地图网”网站的测距功能测得，篇幅所限，具体数据略。

2.2算法分析

本文所建模型属于NP-hard[26]问题，对于大型的此类问题的求解，精确算法以及一般的商业优化软件无能为力，只能借助于启发式或近似算法来求得其近似解。由于上述模型与文献[10]模型类似，因此其求解思路也可用文献[10]提出的人工智能算法——蚁群算法求解。

2.3配置结果

根据文献[10]的确定房山区区级应急物资储备库个数为8个，并利用其提出的人工智能算法——蚁群算法求解，求得如下等级优化配置结果(表2)。

由表2中第1列可知，考虑行政限制条件下的房山区应急物资储备库等级配置，房山区如果在25个乡镇、街道、办事处中选择8个建设区级应急物资储备库，选择的单位为：城关街道、拱辰街道、琉璃河镇、长沟镇、张坊镇、佛子庄乡、史家营乡、燕山地区。

由表2第2列可以得出各区级应急物资储备库服务的乡镇、覆盖半径以及最远服务乡镇。例如，落在城关街道服务范围内的乡级单位为城关街道、周口店地区、石楼镇，覆盖半径为5.7 km，最远服务乡镇为石楼镇。其他区级应急物资储备库的服务情况详见表2，不再赘述。

由表2第3列显示房山区25个乡镇乡镇级应急物资储备库的配置情况。由表2第4列可以得出各乡镇级应急物资储备库服务的村庄、覆盖半径以及最远服务村庄。表2中覆盖半径为 0 km，意指该储备库只为其自身所在乡镇级单位服务。

2.4房山区应急物资储备库等级配置示意图

基于表2，结合原始数据和上述分析，得到房山区应急物资储备库等级优化配置示意图，见图1。

由图1可知，通过本文构建的优化配置模型，房山区8个区级应急物资储备库和25个乡镇级应急物资储备库，形成了层次分明、分布均衡的空间布局。以应急物资储备库为中心的服务区域结构较为紧凑，形成了以储备库为中心的乡镇、村庄组团结构。储备库的这种空间均衡配置有利于房山区应急资源的有效调度与合理配置，实证了本文所建模型的合理性。

2.5房山区应急物资储备库建设相关建议

①要重视房山区应急物资储备库建设中的等级特征，实现区级应急物资储备库重点布局，乡镇级应急物资储备库普及布局(响应北京市政府号召，争取每一乡镇布局1处)。②要均衡布局房山区区级应急物资储备库，实现其等级布局建设的合理性。既要在房山区的较大社区等人口集中的区域建设(如城关街道、拱辰街道、燕山区等)，也要在应急救助区位优越的乡镇(如琉璃河地区、长沟镇、张坊镇、佛子庄乡、史家营乡等)加快建设，做到突发公共事件的有备无患，将房山区可能的灾害损失降到最低。③结合房山区发展规划，要加强与房山区应急物质储备库相关的配套设施建设与活动开展。应保证区、县及以上等级公路设施与房山区应急物质储备库相通。以房山区应急物质储备库为中心，建立乡镇、村级应急物资储备体系，并开展体系内的交流、协作活动。④要注意应急物资储备库建设的协调性。要使房山区应急物质储备库融入居民的实际生产生活，与房山区发展规划相协调；融入北京市应急管理体系，与北京市的建设相协调。⑤房山区应急物资配置中，应坚持“平战结合、因地制宜”原则。要考虑平时物资储备与战时(突发事件下)物资储备的合理比例，并对储备物资按规定时间及时更新。要综合考虑房山区各地区、街道、乡、镇的灾害风险程度、自然环境条件、实际人口密度等，对储备物资进行科学配置，达到资源的有效利用和灾害的有效防范。

表2　房山区应急物资储备库的等级配置结果

续表2

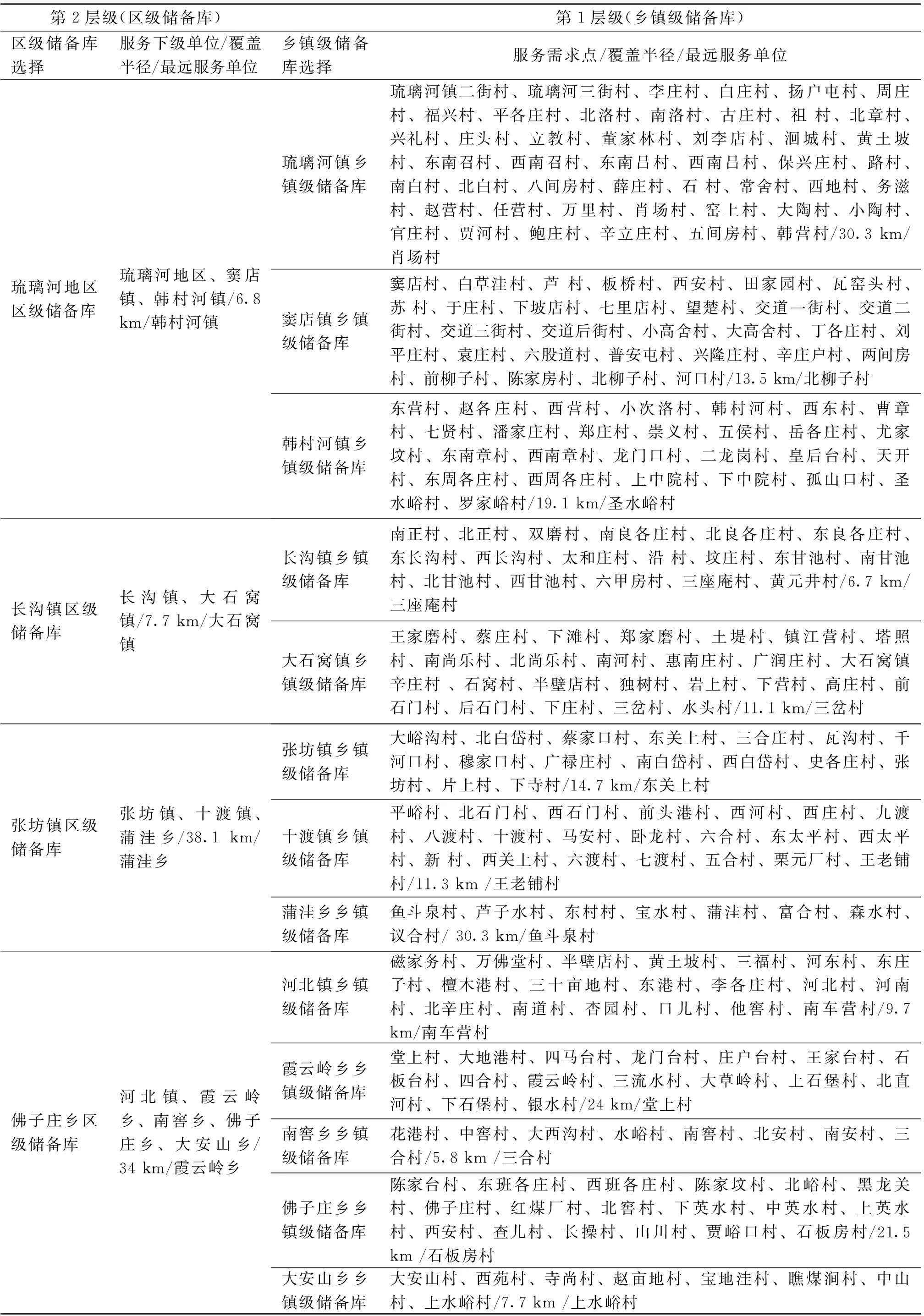
第2层级(区级储备库)第1层级(乡镇级储备库)区级储备库选择服务下级单位/覆盖半径/最远服务单位乡镇级储备库选择服务需求点/覆盖半径/最远服务单位琉璃河地区区级储备库琉璃河地区、窦店镇、韩村河镇/6.8km/韩村河镇琉璃河镇乡镇级储备库琉璃河镇二街村、琉璃河三街村、李庄村、白庄村、扬户屯村、周庄村、福兴村、平各庄村、北洛村、南洛村、古庄村、祖村、北章村、兴礼村、庄头村、立教村、董家林村、刘李店村、洄城村、黄土坡村、东南召村、西南召村、东南吕村、西南吕村、保兴庄村、路村、南白村、北白村、八间房村、薛庄村、石村、常舍村、西地村、务滋村、赵营村、任营村、万里村、肖场村、窑上村、大陶村、小陶村、官庄村、贾河村、鲍庄村、辛立庄村、五间房村、韩营村/30.3km/肖场村窦店镇乡镇级储备库窦店村、白草洼村、芦村、板桥村、西安村、田家园村、瓦窑头村、苏村、于庄村、下坡店村、七里店村、望楚村、交道一街村、交道二街村、交道三街村、交道后街村、小高舍村、大高舍村、丁各庄村、刘平庄村、袁庄村、六股道村、普安屯村、兴隆庄村、辛庄户村、两间房村、前柳子村、陈家房村、北柳子村、河口村/13.5km/北柳子村韩村河镇乡镇级储备库东营村、赵各庄村、西营村、小次洛村、韩村河村、西东村、曹章村、七贤村、潘家庄村、郑庄村、崇义村、五侯村、岳各庄村、尤家坟村、东南章村、西南章村、龙门口村、二龙岗村、皇后台村、天开村、东周各庄村、西周各庄村、上中院村、下中院村、孤山口村、圣水峪村、罗家峪村/19.1km/圣水峪村长沟镇区级储备库长沟镇、大石窝镇/7.7km/大石窝镇长沟镇乡镇级储备库南正村、北正村、双磨村、南良各庄村、北良各庄村、东良各庄村、东长沟村、西长沟村、太和庄村、沿村、坟庄村、东甘池村、南甘池村、北甘池村、西甘池村、六甲房村、三座庵村、黄元井村/6.7km/三座庵村大石窝镇乡镇级储备库王家磨村、蔡庄村、下滩村、郑家磨村、土堤村、镇江营村、塔照村、南尚乐村、北尚乐村、南河村、惠南庄村、广润庄村、大石窝镇辛庄村、石窝村、半壁店村、独树村、岩上村、下营村、高庄村、前石门村、后石门村、下庄村、三岔村、水头村/11.1km/三岔村张坊镇区级储备库张坊镇、十渡镇、蒲洼乡/38.1km/蒲洼乡张坊镇乡镇级储备库大峪沟村、北白岱村、蔡家口村、东关上村、三合庄村、瓦沟村、千河口村、穆家口村、广禄庄村、南白岱村、西白岱村、史各庄村、张坊村、片上村、下寺村/14.7km/东关上村十渡镇乡镇级储备库平峪村、北石门村、西石门村、前头港村、西河村、西庄村、九渡村、八渡村、十渡村、马安村、卧龙村、六合村、东太平村、西太平村、新村、西关上村、六渡村、七渡村、五合村、栗元厂村、王老铺村/11.3km/王老铺村蒲洼乡乡镇级储备库鱼斗泉村、芦子水村、东村村、宝水村、蒲洼村、富合村、森水村、议合村/30.3km/鱼斗泉村佛子庄乡区级储备库河北镇、霞云岭乡、南窖乡、佛子庄乡、大安山乡/34km/霞云岭乡河北镇乡镇级储备库磁家务村、万佛堂村、半壁店村、黄土坡村、三福村、河东村、东庄子村、檀木港村、三十亩地村、东港村、李各庄村、河北村、河南村、北辛庄村、南道村、杏园村、口儿村、他窖村、南车营村/9.7km/南车营村霞云岭乡乡镇级储备库堂上村、大地港村、四马台村、龙门台村、庄户台村、王家台村、石板台村、四合村、霞云岭村、三流水村、大草岭村、上石堡村、北直河村、下石堡村、银水村/24km/堂上村南窖乡乡镇级储备库花港村、中窖村、大西沟村、水峪村、南窖村、北安村、南安村、三合村/5.8km/三合村佛子庄乡乡镇级储备库陈家台村、东班各庄村、西班各庄村、陈家坟村、北峪村、黑龙关村、佛子庄村、红煤厂村、北窖村、下英水村、中英水村、上英水村、西安村、查儿村、长操村、山川村、贾峪口村、石板房村/21.5km/石板房村大安山乡乡镇级储备库大安山村、西苑村、寺尚村、赵亩地村、宝地洼村、瞧煤涧村、中山村、上水峪村/7.7km/上水峪村

续表2

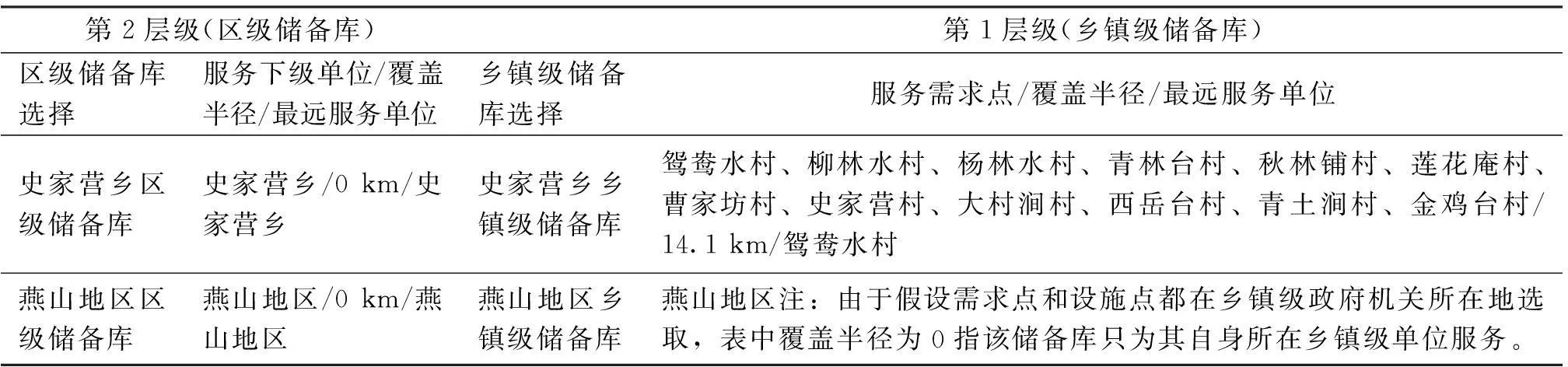
第2层级(区级储备库)第1层级(乡镇级储备库)区级储备库选择服务下级单位/覆盖半径/最远服务单位乡镇级储备库选择服务需求点/覆盖半径/最远服务单位史家营乡区级储备库史家营乡/0km/史家营乡史家营乡乡镇级储备库鸳鸯水村、柳林水村、杨林水村、青林台村、秋林铺村、莲花庵村、曹家坊村、史家营村、大村涧村、西岳台村、青土涧村、金鸡台村/14.1km/鸳鸯水村燕山地区区级储备库燕山地区/0km/燕山地区燕山地区乡镇级储备库燕山地区注:由于假设需求点和设施点都在乡镇级政府机关所在地选取,表中覆盖半径为0指该储备库只为其自身所在乡镇级单位服务。

3结论与研究展望

3.1结论

提出了小城镇应急物资储备库等级选址问题并构建模型，厘清了小城镇应急物资储备库等级配置的三级优化思路。结合房山区的需要，完成了房山区8个区级应急物资储备库的优化选址，并实现8个区级应急物资储备库与25个乡镇应急物资储备库的空间联系优化，绘出了优化配置图(图1)，提出相关建议。成果对我国小城镇应急设施优化选址与配置，乃至小城镇的防灾规划有一定的指导意义，可为其提供定量分析思路与方法，增加了相关工作的科学性。此外，小城镇应急公共设施中，除了应急物资储备库外，消防设施、急救中心、避难场所建设也是当前政府和学者关注的焦点，本文成果也能为之提供一定的借鉴依据。

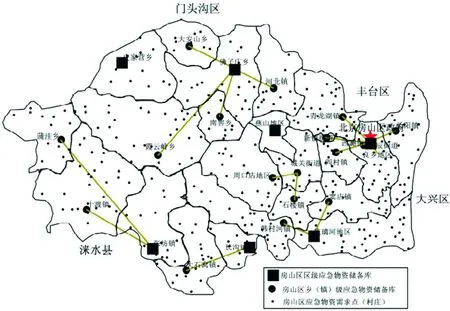
图1　房山区应急物资储备库等级优化配置示意图

3.2研究展望

首先，本文仅考虑应急物资储备库存在等级情景下的优化配置问题，缺乏不考虑等级和考虑等级两种情景下的优化效果对比，此方面可以作进一步的研究。其次，本文仅考虑了效率准则下(最大覆盖等级设施选址准则下)的小城镇应急物资储备库等级优化配置问题，因此，拓展的另一思路就是考虑公平准则下的(如最小方差、基尼系数最小、权重距离方差最小原则等)的小城镇应急物资储备库等级优化配置问题。最后，等级选址问题的算法求解问题一直是激发学者研究兴趣的重要领域，对超级节点算法的合理性及其进一步优化的探讨也值得期待。

参考文献:

[1]ReVelle C S, Eiselt H A, Daskin M S. A bibliography for some fundamental problem categories in discrete location science[J]. European Journal of Operational Research, 2008, 184 (3): 817-848.

[2]ReVelle C S, Eiselt H A. Location analysis: a synthesis and survey[J]. European Journal of Operational Research, 2005, 165(1): 1-19.

[3]Eiselt H A, Sandblom C L. Decision analysis, location models, and scheduling problems[M]. Springer-Verlag, Berlin-Heidelberg-New York, 2004.

[4]Arabani A B, Farahani R Z. Facility location dynamics: An overview of classifications and applications[J]. Computers & Industrial Engineering, 2012, 62(1): 408-420.

[5]Francis R L, McGinnis L F, White A. Location analysis[J]. European Journal of Operational Research, 1983,12(3): 220-252.

[6]Brandeau M L. An overview of representative problems in location research[J]. Management Science, 1989, 35(6):645-674.

[7]Drezner Z, Hamacher H W. Facility location: applications and theory[M]. Berlin: Springer, 2002.

[8]Farahani R Z, Hekmatfar M. Facility Location: Concepts, Models, Algorithms and Case Studies[M]. Berlin: Physica-Verlag, 2009.

[9]陆相林, 侯云先,林文,等. 基于设施选址理论的小城镇应急医疗服务中心功能优化[J]. 经济地理, 2011, 31(7):1119-1123.

[10]陆相林, 侯云先, 林文,等. 基于选址理论的小城镇应急物资储备库优化配置――以北京房山区为例[J]. 地理研究, 2011, 30(6):1091-1099.

[11]Narula S C. Hierarchical location-allocation problems: a classification scheme[J]. European Journal of Operational Research, 1984, 15(1): 93-99.

[12]Marianov V, Serra D. Hierarchical location-allocation models for congested systems [J]. European Journal of Operational Research, 2001, 135(1):195-208.

[13]Serra D, ReVelle C. The pq-median problem: location and districting of hierarchical facilities[J]. Location Science, 1993, 1(4): 299-312.

[14]Sahin G , Süral H. A review of hierarchical facility location models[J]. Computers & Operations Research , 2007, 34(8) : 2310-2331.

[15]陆相林, 侯云先. 基于设施选址理论的中国国家级应急物资储备库优化配置[J]. 经济地理, 2010, 30(7):1091-1095.

[16]陈志宗, 尤建新.城市防灾减灾设施的层级选址问题建模[J].自然灾害学报. 2005, 14(2): 131-135.

[17]冉岚. 从汶川地震看国家物资储备建设[J]. 宏观经济管理, 2008 (9): 60-62.

[18]杨子健. 建设国家战略物资储备基地建议[J]. 宏观经济管理, 2011, (1): 37-38.

[19]张永领. 我国应急物资储备体系完善研究[J].管理学刊, 2010,23(6):54-57.

[20]郭子雪,齐美然,张强. 应急物资储备库最小加权距离选址模型[J]. 计算机工程与应用, 2009, 45(34): 195-198.

[21]郭子雪,齐美然,张玉芬. 提高河北省突发事件应急处置能力的对策[J]. 保定学院学报, 2011, 24(2): 903-910.

[22]冯凯,徐志胜,冯春莹,等.小城镇突发公共事件应急决策系统的研究[J].灾害学,2005,20(2):6-10.

[23]卓力格图,王罡.新型城镇化建设背景下的防震减灾创新发展研究初探[J].灾害学,2015,30(3):183-185.

[24]孙明,王绍玉,闫建新.村镇公共安全评价体系研究——以河北省沧州市南大港一分区为例[J].灾害学,2015,30(1):115-119.

[25]吴宗之, 刘茂. 重大事故应急救援系统及预案导论[M]. 北京: 冶金工业出版社, 2003.

[26]Kariv O,Hakimi S.An algorithm approach to network location problem[J].SIAM Journal of Applied Mathematics,1979,37(4):513-560.

Hierarchical Allocation of Emergency Material Depository in Small Town Based on Facility Location Theory——A Case Study of Fangshan District in Beijing

Lu Xianglin1, 2and Miao Changhong1

(1.KeyResearchInstituteofYellowRiverCivilizationandSustainableDevelopment&CollegeofEnvironment&Planning,HenanUniversity,Kaifeng475001,China; 2.DepartmentofEconomicsandManagementofShijiazhuangUniversity,Shijiazhuang050035,China)

Abstract:According to the deployment of “Small town, grand strategy”, urbanization of China has entered a key stage. However, it is confronted with a great challenge for China to strengthen emergency management of small town. Emergency management for small town needs a resource allocation system with flexibility, fluency, punctuality, rationality and effectiveness. Based on the plan of Beijing government, every town in Beijing will establish one emergency material depository before 2020. There are few documents analyzing the allocation of small-town emergency material depository of China with quantitative methods. Also, the traditional facility location problems think little of the satisfaction difference between demand points in the covering radius of facility. In the light of this situation, we present a hierarchical maximal covering location problem considering the demand satisfaction difference between demand points in the domain of facility covering radius and formulate a maximal covering model as an integer programming under the goal of maximizing the total satisfaction of demand points．After investigating the characteristics of the model formulated，we introduce super-node algorithm to solve the considered problems. Then, we get the allocation result of emergency material depository of Fangshan District in Beijing. The computational result have shown that the model we proposed generate facility location solutions in a more effective manner. Finally, we also propose extensions to our research.

Key words:facility location; emergency material depository; hierarchical maximal covering; small town; Fangshan District of Beijing

doi:10.3969/j.issn.1000-811X.2016.02.031

中图分类号：X43；F224.3

文献标志码：A

文章编号：1000-811X(2016)02-0156-08

作者简介：陆相林(1977-)，男，河南台前人，博士，副教授，研究方向为管理系统优化与物流管理，区域旅游发展. E-mail：luxianglin1@126.com

基金项目：国家社会科学基金项目(13BGL130)；2014年河北省高等学校青年拔尖人才计划项目(BJ201409)

*收稿日期：2015-08-31修回日期：2015-10-22

陆相林，苗长虹. 小城镇应急物资储备库等级优化配置模型与实证——以北京市房山区为例[J].灾害学, 2016,31(2):156-163.[ Lu Xianglin and Miao Changhong. Hierarchical Allocation of Emergency Material Depository in Small Town Based on Facility Location Theory——A Case Study of Fangshan District in Beijing[J].Journal of Catastrophology, 2016,31(2)：156-163.]