基于重力测量卫星的重力梯度辅助导航研究
秦宇杰,王可东
(北京航空航天大学宇航学院,北京 100191)
基于重力测量卫星的重力梯度辅助导航研究
秦宇杰,王可东
(北京航空航天大学宇航学院,北京 100191)
摘要:惯性导航系统的误差随着时间而不断累积,而战时很可能无卫星信号来校正惯导仪器,因此,完全自主的重力梯度辅助导航技术越来越受到重视。本文以亚音速飞行的巡航导弹为例,分析了重力梯度匹配辅助导航系统的关键技术,并针对等值线匹配算法在大初始误差条件下易陷入局部最优点的问题,引入了衰减绝对差算法进行粗匹配,同时,改进了其采样策略,避免了实时性差的缺陷。仿真结果表明,重力梯度匹配辅助导航的精度限制在一个网格,且能适应大初始误差的情况。
关键词:惯性导航;辅助导航;重力梯度;等值线匹配
0引言
目前,各种载体(如导弹、潜艇)一般均以惯性导航系统(INS)为主导航系统。惯性导航具有自主性,不受时间、地点、天气等外界条件限制,为载体的隐蔽飞行创造了有利条件。但是INS的误差随着时间而积累,无法进行长时间的导航定位,因此需要外部辅助定位的方法对惯性导航系统进行修正[1-3]。现行的外部辅助导航技术中,卫星导航系统(GNSS),尤其是全球定位系统(GPS)成为最常用的辅助定位方法[4]。但是,卫星导航定位系统极易受到外界的干扰,尤为重要的是,在战时,很有可能无GPS卫星信号来修正INS定位误差。
因此,在没有卫星信号的情况下,为了提高导航系统的性能,地形辅助导航[5]和重力辅助导航[6]等基于地理特征的辅助导航技术近年来得到了越来越多的研究,其中尤以重力辅助导航的无源性最好。重力场辅助惯性导航的一个突破性进展是,20世纪80年代,Textron利用重力传感器系统(GSS)在移动载体上实现了重力梯度测量[7]。重力梯度测量消除了重力传感器获得的载体加速度信号,可以直接与已有的重力梯度数据地图进行匹配。1995年Gleason[8]讨论了重力梯度图形匹配辅助导航系统的各种工程实际问题,重点分析了如何利用快速傅里叶变换(FFT)的方法实现重力梯度网格的绘制;同时分析了载体速度、高度、重力梯度仪噪声水平和采样速率对重力梯度图形匹配辅助导航系统的影响等。
本文以此为基础,以在海域以亚音速飞行的巡航导弹为例,重点研究在无卫星信号辅助导航的情况下,重力梯度辅助导航系统的可行性。
1重力梯度辅助导航的关键技术
重力梯度匹配辅助导航系统是利用重力梯度基准图组成的基本信息数据库特征获取载体位置信息的导航技术。重力梯度匹配和地形匹配技术较为相似,到目前为止已经发展了很多匹配算法,如 TERCOM 法、ICCP 法、SITAN 法和神经网络法等。但重力梯度匹配辅助导航技术的实现主要受到重力梯度图获取和重力梯度仪的发展两方面的限制。由于种种条件限制,很少有国家进行重力梯度测量,因此目前还没有任何有关全球重力梯度的数据库问世。但是,随着卫星重力测量技术的发展,通过卫星获取全球重力梯度模型成为可能,而且随着技术的发展,在空间分辨率和精度方面都得到了显著的提升,有可能满足重力梯度辅助导航的应用要求,如美德GRACE卫星和欧空局GOCE卫星。目前,为了对重力梯度匹配辅助导航技术进行研究,获取重力梯度基准数据的方法主要集中在利用现有的高精度地形高程和重力异常数据来模拟重力梯度数据(即重力梯度的正演问题)的研究上,已有近四十年的发展历史,主要有基于傅氏变换的Parker方法和Forsberg方法、球谐模型计算法[9]、数值积分法、棱柱法以及地形与重力模型的联合构图法等正演方法。
另外,由于重力梯度仪的技术比较复杂,许多国家缺乏制造重力梯度仪的能力。对重力梯度辅助导航系统的研究并未广泛展开,只集中在少数国家。目前主要的重力梯度仪研究水平[10],如表1所示。

表1 重力梯度仪性能规格
采用球谐模型计算思路,对国际海洋与大气管理中心(NOAA)与国际地理调查中心(NGS)利用EGM96模型编写的网格化计算全球重力场信息(重力位、重力、重力梯度)软件进行改进,获取了基于EGM2008模型的重力梯度数据,并采用Kriging插值方法进行数据内插,生成本文仿真用的重力梯度基准图,如图1所示为生成的分辨率为5′×5′的马里亚纳群岛的区域重力梯度基准图,可看到扰动重力垂直梯度与地球地形具有高度的相关性,其分布图与地球地质构造的变化特征及大陆边界轮廓相当吻合,在大陆边界、海沟、岛链、断槽等处尤为明显,这从侧面验证了获取的重力梯度基准图的有效性。重力梯度仪测量误差采用0.3E的水平。
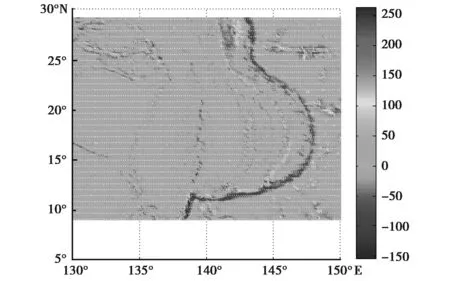
图1 区域重力梯度图
2等值线匹配算法分析及改进
基于等值线的迭代最近点匹配算法ICCP算法[11-12]是图像配准中ICP算法的一个特例。总的来说,ICCP算法就是不断寻找刚性变换(旋转和平移),使惯导INS所测量的数据尽可能地逼近其相应的等值线,得到满足一定迭代条件的极值点作为修正点,从而达到改进运动估计的目的。
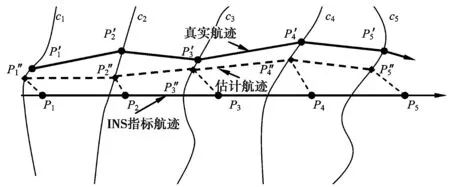
图2 ICCP算法原理
如果假设:虽然INS输出量存在着一定的累积误差,但其指示位置与载体的真实位置相距不远。目标函数可表达为
(1)
式中: E为目标函数,即总误差,距离度量,取单位为m; d(p,q)为p与q之间的距离; xi为估计点{P″i}的位置,yi为xi在等值线上的投影或离等值线的最近点的位置; ai为INS指示位置; K为刚度系数。如式(1)所示的目标函数的第一项是将估计点限制在INS指示位置附近,第二项是使估计点向量测值等值线靠拢。
所以本算法认为真实位置在INS指示位置的附近,并按照最近路径原则投影到相应的等值线上,实现对INS位置的初始估计。因此,为提升ICCP算法适应大初始误差的性能,本文引入了粗匹配方法,利用快速收敛、收敛范围大的衰减绝对差(简称“衰减AD”)算法进行替代航迹的选取。
将衰减AD算法的量测记为αAD,粗匹配的目的就是计算获得该量测值。定义k时间点的单点误差表示为
em,n(k)=Γmeasure(k)-Γmap(xk+m,yk+n),
(2)
式中:m和n为搜索窗口的长宽;xk和yk表示是搜索窗口的基准位置;Γmeasure表示重力梯度的量测值;Γmap为重力梯度基准数据。对于每一个时刻k,em,n(k)为(2m+1)×(2n+1)维矩阵。
定义αAD
αADm,n=|em,n(k)|+α·|em,n(k-1)|+α2·
|em,n(k-2)|+…+αk-2·
|em,n(2)|+αk-1·|em,n(1)|
(3)
αAD也是一个(2m+1)×(2n+1)维矩阵。
这里选取αAD最小的t个点,并且这t个点都要小于阈值C(小于的数目记为s(k),主要用来判断发散情况,当没有一个值满足时,则以惯导指示为中心重新启动衰减匹配),利用这几个值的大小决定对应的权重,然后再进行加权[13]计算一个估计位置作为替代点。
即,设满足要求的各点位置表示为[mini)T,概率为βi(k),且
(4)
取
(5)
tbi=total0/αADmi,ni,i=1,2,…,t,
(6)
(7)
βi(k)=tbi/total1,i=1,2,…,t
(8)
最后的估计位置表示为
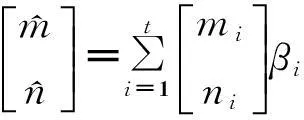
(9)
利用概率数据关联的思想,将所有点都放入考虑范围之内,只是将前面的值都乘上一个衰减系数α(0<α<1,通常取α=0.95~0.99),最终获得INS指示航迹的替代航迹进行等值线优化。
另外,ICCP算法与TERCOM算法一样,是一种批处理或后验估计方法,并不是逐点匹配,必须在获取足够多的点数后才能进行一次匹配,所获得的点数一般至少需要大于3个,序列匹配可有效提高算法的容错能力,使其具有较好的稳定性,但是算法却存在实时性差的问题。本文采用移动的ICCP算法来改进其实时性差的缺陷。
所谓的移动ICCP算法就是借鉴计算机编程中的移位寄存器思想,即设匹配序列长度为N,当采样到最新的采样点PN+1时,经过移位舍弃第一个采样点P1,再以新的采样点集Pi(i=2,3,…,N+1)进行匹配计算,以此类推就可实现每采样到一个量测值进行一次匹配计算,当然,还可控制移位的长度,使每采样m个点进行一次匹配。
移动的ICCP算法与原算法的最大不同在于:只需一次采样到N个值,之后的匹配位置即可实时给出。另外,由于前后两次匹配所用的采样点集只有m个值不同,因此点集中有N-m个点的等值线以及权值无需重新提取及计算,从而降低了算法的复杂度。因此,移动的ICCP算法是一种简便的方法,它通过改变原ICCP算法的采样结构便可解决其实时性差的缺陷。
3仿真及可行性分析
综上所述,重力梯度匹配辅助导航系统的实现主要包含重力梯度基准数据的获取、实时重力梯度数据的测量和匹配算法的实现三个方面。为验证重力梯度辅助导航的可行性,以亚音速飞行的巡航导弹为例,在MATLAB8.0平台下对基于改进的ICCP算法的重力梯度辅助定位方法进行仿真分析。仿真平台主要流程包括以下几个方面:
1) 调取重力梯度基准图,并显示绘制的等值线;
2) 设置INS的误差模型及初始误差,初始化载体的运动状态;
3) 设置ICCP算法仿真参数,如匹配截止门限、最大迭代次数、匹配序列长度和移动间隔。
4) 输入航迹节点,进行航迹规划;
5) 进行粗匹配,累积匹配序列,当达到匹配长度时进行ICCP调整,包括误匹配判断环节;
6) 判断系统是否收敛,若收敛系统进入跟踪模式,改为移动的ICCP调整算法;
7) 输出匹配航迹给INS来补偿其误差积累;
8) 仿真结束,输出结果以及图表。
仿真的基本条件为:仿真区域的重力梯度基准数据如图3所示,为一幅采用球谐模型计算和Kriging插值方法获取的基于EGM2008模型的基准图,为一海域,重力梯度异常最大值为224.279 6E,最小值为-92.578 7E,平均值为-0.848 4E,格网数600×600,格网间距为30″(约为900m),起始经纬度为(146°,18°)。载体航行速度为250m/s.SINS初始经纬度误差均为0.06°(约为10个网格);加速度计X、Y、Z轴的漂移均为10-4g;陀螺仪X、Y、Z轴的漂移均为0.01°/h;重力梯度仪测量误差是0.1E的系统噪声叠加方差为0.3E的白噪声。总航行时间约为1 200s.
仿真结束时,SINS指示的航迹误差已达到11.4个网格;而改进的ICCP算法匹配位置误差维持在1个网格左右,具体结果对比如图4所示。

图3 仿真海域的重力梯度

图4 改进ICCP算法匹配结果
表2示出10次试验的仿真结果,INS指示的初始误差从0.01~0.2之间变化。
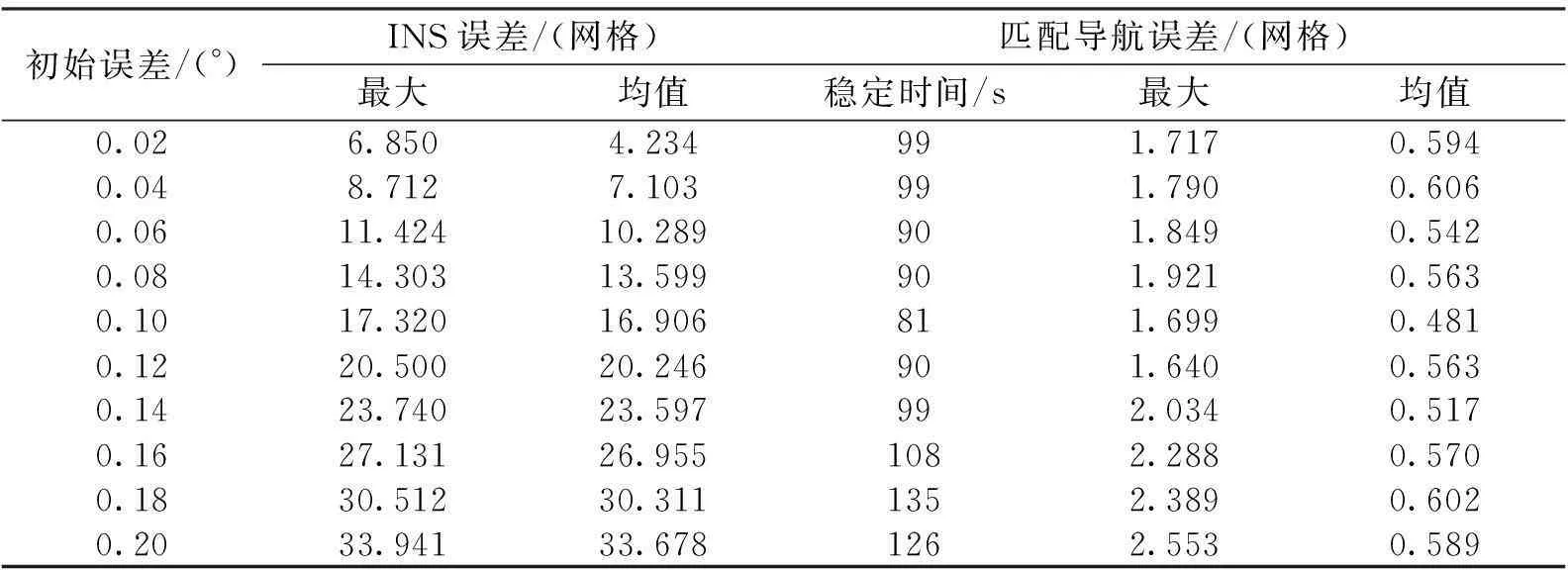
表2 改进ICCP算法匹配结果
由表2可知,重力梯度匹配辅助导航的改进ICCP算法能够适应较大的INS指示误差的情况,平均匹配误差小于一个网格。如在初始误差为10个网格的情况下快速匹配成功,在90 s后进入跟踪模式;并能在陀螺仪漂移为0.01°/h、加速度计漂移为10-4g的低精度INS指示的条件下稳定跟踪,匹配误差的均值约为0.542个网格。
4结束语
重力梯度匹配辅助导航系统是一种完全自主的导航系统,随着现代重力场测量技术水平的日益提高,重力梯度匹配辅助导航系统具有更加重要的现实意义,不仅可以克服和弥补我国惯性导航仪器精度较低的缺陷,还可以克服和弥补战时很可能无卫星导航信号来校正惯导仪器的问题。仿真结果表明,改进的ICCP算法使重力梯度辅助导航的匹配精度限制在一个网格,且能适应大初始误差的情况。因此,随着重力梯度测量卫星的发展,重力梯度基准数据在空间分辨率和精度方面都将得到显著的提升,网格间距越小,匹配精度越高;同时,重力梯度仪的研制和发展,也是重力梯度辅助导航的实际应用的必要条件。
我国在重力仪、高精度INS和匹配算法等方面都有一定的基础,重力测量卫星的相关的理论研究和方案论证等工作也已经开展,因此,未来发展重力梯度辅助导航系统是可行的,且具有重要的现实意义。
参考文献
[1] LOWREYS J A, SHELLENBARGER J C. Passive navigation using inertial navigation sensors and maps [J]. Naval Engineers Journal, 1997, 109(3): 245-251.
[2] 成怡.多源海洋重力数据融合技术研究[D].哈尔滨:哈尔滨工程大学,2008:11-26.
[3] JEKELI C. Inertial navigation systems with geodetic applications [M]. Walter De Gruyter, New York, 2001.
[4] FARRELL J A, BARTH M. The global positioning system & inertial navigation [M]. McGraw-Hill, New York, 1999.
[5] HUGH R, STEVEN K, LOUIS M. Geophysical navigation technologies and applications [C].//IEEE Position, Location and Navigation Symposium, Monterey, 2004: 618-624.
[6] HUGH R, LOUIS M, ROBERT A. Next generation marine precision navigation system [C].//IEEE 2000 Position, Location and Navigation Symposium, San Diego, 2000: 200-206.
[7] 蔡体菁,周百令. 重力梯度仪的现状和前景[J].中国惯性技术学报, 1999,7(1):39-42.
[8] GLEASON D M. Passive airborne navigation and terrain avoidance using gravity gradiometry [J]. AIAA Journal of Guidance, Control, and Dynamics, 1995, 18(6): 1450-1458.
[9] JUSTIN A R. Gravity gradiometer aided inertial navigation within NON-GNSS environments [D]. Doctor of Philosophy Department of Aerospace Engineering, 2008: 21-24.
[10]刘凤鸣. 重力梯度辅助导航定位技术研究[D].哈尔滨:哈尔滨工程大学, 2010:61-82.
[11]BEHZAD K P, BEHROOZ K P. Vehicle localization on gravity maps [C].//Proceedings of SPIE—The International Society for Optical Engineering, 1999(3693): 182-191.
[12]BISHOP G C. Gravitational field maps and navigational errors [J]. IEEE Journal of Oceanic Engineering, 2002,27(3): 726-737.
[13]冯庆堂,沈林成,常文森. 基于概率数据关联的地形辅助导航算法[J].宇航学报, 2003,24(5):440-443,462.
秦宇杰(1989-),男,研究生,主要从事重力匹配导航技术研究。
王可东(1975-),男,博士,副教授,主要从事地形匹配和组合导航技术研究。
Research on the Gravity Gradient Aided Navigation System Based on Gravity Satellite
QIN Yujie,WANG Kedong
(SchoolofAstronautics,BeihangUniversity,Beijing100191,China)
Abstract:The inertial navigation system’s (INS) position error grows larger and larger as time goes on; it is likely to happen that no satellite signal to amend the INS’s instrument in wartime, therefore, there is a growing emphasis on the gravity gradient aided navigation technology which is completely independent. This paper focuses on the gravity gradient aided navigation key technologies, and in order to overcome the defect that navigation accuracy of gravity gradient aided navigation algorithm is not high in large initial matching error, the attenuation absolute difference algorithm is introduced to gravity gradient aided navigation, meanwhile, improved the sampling strategy to avoid the bad real-time defects. Simulation results show that the accuracy of gravity gradient aided navigation is a grid around, even in the case of larger initial errors.
Keywords:Inertial navigation system; aided navigation; gravity gradient; iterative closest contour point
作者简介
中图分类号:V249.32+8
文献标志码:A
文章编号:1008-9268(2016)01-0019-05
收稿日期:2015-10-20
doi:10.13442/j.gnss.1008-9268.2016.01.004
资助项目: 国家自然科学基金(批准号:61573040)
联系人: 秦宇杰 E-mail: qyujie2007@sina.com

