混凝土受力本构关系及展望
朱志永 金辉
1武汉平煤武钢联合焦化公司(430082)2河南建筑职业技术学院(450003)
混凝土受力本构关系及展望
朱志永1金辉2
1武汉平煤武钢联合焦化公司(430082)2河南建筑职业技术学院(450003)
通过混凝土本构模型的研究与分析,将混凝土本构模型分为以下几类,根据其特点和作用解决工程中的相应问题,并将这些理论结合微观观察与分析作出对于未来的展望。
弹性本构模型;塑性本构模型;内蕴时间本构模型;断裂力学本构模型;损伤力学本构模型
1 混凝土本构模型
混凝土是土木工程结构中应用极为广泛的材料,在相当长时间内依靠经验公式进行设计与分析。近几十年来,随着电子计算机的普及,混凝土非线性有限元分析得到了很大发展,有关混凝土的本构关系得到了广泛而深入的研究。混凝土本构模型主要分为以下几类:弹性本构模型、弹塑性本构模型、内蕴时间本构模型、断裂力学本构模型、损伤本构模型以及各种模型组合而成的模型。
1.1 弹性本构模型
弹性力学模型是最早出现的材料本构模型也是最简单的本构模型,在早期解决工程问题中起到了重要的作用。直至现在,较多的结构分析程序仍是采用的弹性模型。其典型特点是:除去外力变形恢复到初始状态,变形可逆,不产生能量耗散。弹性模型又分为线弹性模型和非线性弹性模型。
1)线弹性本构模型
线弹性模型中,应力张量分量σij与应变张量分量εkl之间满足线性关系,即广义虎克定律:

式中,Cijkl是四阶弹性刚度张量的分量,在最一般的情况下包括81个材料常数。如果材料是正交各向异性的,独立的材料常数可减少至9个,如果材料是各向同性的,材料常数减少为两个,可用弹性模量E和波松比ν来表示,此时,应力-应变关系可表达为:

线弹性虎克定律表达简单,材料参数容易从简单实验测定,在混凝土结构分析中一直很有吸引力,尤其是在混凝土处于较低的应力状态(开裂以前)可以取得满足工程要求的计算结果,但在高应力状态下误差较大。
2)非线弹性本构模型
超过线弹性变形阶段的混凝土在进一步受力过程中会产生明显的不可逆变形,但如果仅考虑单调加载可以采用非线性弹性模型,因此将非线性弹性模型应用于混凝土只是一种近似。应力应变的非线性关系能较为精确的描述混凝土峰值应力前的变形特性,且计算简单。这种模型又分为三种:
1)Cauchy非线弹性模型
这是最简单的一种非线性弹性模型,是对线弹性模型的改进。该模型假定应力只依赖于应变,应变也只依赖于应力,与变化路径无关,各向同性情况下全量形式的应力-应变表达式为:

该模型只是一种经验模型,尤其适合于比例加载情况,但不严格满足热力学基本定律,不同加载路径下得不到统一的应变能表达式,因此应力应变之间不存在功共轭关系。复杂加载条件下误差较大。
2)Hyperelastic非线弹性模型


该模型满足质量守恒定律,不仅能描述混凝土力-位移的非线性而且能描述混凝土的膨胀、应力引起的各向异性。Cauchy非线性弹性模型及Hyperelastic非线弹性模型在有限元模拟中可采用不断变化的割线模量。较为著名的混凝土非线性弹性本构模型如Cedolin et al.模型,Kotsovos et al.模型,Ottosen模型等都是属于此类采用全量型本构模型。
3)Hypoelastic非线弹性模型
该模型认为材料的力学性能不仅与现时应力及应变状态有关,而且还与达到此状态的变化路径有关,为反映路径相关性,一般采用增量形式表达应力-应变关系:

由于应力-应变关系采用增量形式表达,因此在有限元模拟中可采用不断变化的切线模量,属于此类的非线性弹性本构模型有著名的Darwin和Pecknold构本构模型(1977)以及Elwi和Murray模型(1979)。
弹性模型最大的缺点是:不能考虑加载过程中的不可逆变形,不能处理卸载以及循环加卸载情况。我国现行混凝土结构设计规范所采取的方法是:进行结构内力计算采用线弹性模型,而对于特别重要的或受力状况特殊的大型杆系结构和二维、三维结构必要时尚应对结构整体或其部分进行受力全过程的非线性分析,而该非线性所采用的就是非线性弹性本构模型。
作为弹性模型的重要辅助控制部分,破坏准则是必不可少的。破坏准则可以理解为弹性材料的应力状态上限,当应力状态超出应力空间的破坏面时,混凝土失效并退出工作。上世纪60年代以来,各国学者在混凝土多轴强度实验研究基础上提出了多种破坏准则,破坏面由3~5个材料参数控制,代表性的有:Bresler-Pister准则、Reimann准则、Ottosen准则、Hsieh-Ting-Chen准则、Willam-Warnke准则、Kotsovos准则、Podgorski准则、过镇海准则等。
1.2 塑性本构模型
以屈服函数为基础的塑性理论在解决金属类晶体延性材料问题方面取得了很大的成就。经典弹塑性理论主要指塑性增量理论(全量塑性理论仅能用于简单加载情况,随着数值方法及计算机技术的发展现已很少采用)是描述材料在塑性状态应力与应变增量之间关系的本构理论,在实际数值方法中一般按加载过程积分获得整个加载历史的力-变形响应。塑性本构理论包括如下必不可少的组成部分:屈服准则、塑性流动准则(可以时相关联或非相关联的)、塑性强化准则以及加载-卸载准则。对某一特定的工程材料,采用不同的屈服函数及相应的塑性势函数可以产生不同的塑性模型。
塑性理论经过数百年的发展,在各国学者不懈的努力下已经发展成为一套完整的理论体系,在数学表达上是严格的,不仅能合理用于各种金属材料,而且经过修正可以广泛适用于岩土及混凝土材料。传统塑性理论的很多基本假设,如静水压力不影响屈服、体积变化是弹性的、剪应力不引起塑性体积变化、塑性应变增量与屈服面正交等是不适用于岩土、混凝土类材料的,塑性理论应用于摩阻类材料必须突破这些限制。广义塑性理论成为解决这类问题的理论依据。
塑性理论用于混凝土最大也是最明显的缺点就是不能很好地处理峰值应力后的软化问题。这是因为按照Drucker公设,以定义在应力空间中的屈服函数为基础的塑性模型只能处理稳定材料(稳定材料)问题,而按照Il’yushin公设,定义在应变空间的塑性模型则可以处理软化问题,但缺乏应变空间屈服函数的实验验证,得不到广泛的应用。而与损伤理论结合的塑性理论可通过损伤理论很好地解决软化问题,这也是文章的主要任务。
较为著名的针对于混凝土的塑性模型主要有:Chen-Chen模型、Han-Chen模型、Chen模型、Fardis-Chen模型、Klinsinski-Mroz模型、Dvorkin模型、Read-Hegemier,Onateet al.模型、Pietruszczak et al.模型、Ohtani-Chen模型等。
1.3 内蕴时间本构模型
内蕴时间理论是一种基于不可逆热力学框架的材料本构理论,由Valanis于1971年提出,我国学者范镜泓为该理论的推广做了大量的工作,具体研究了多种材料的本构模型,并对材料的本构不变性给予了数学证明。该理论的基本假设为:塑性和粘塑性等耗散材料内的任一点的现时应力状态是该点邻域内整个变形和温度历史的泛函,且该历史是用一个取决于变形中的材料特性和变形程度的内蕴时间标度Z来度量的。
Valanis于1978年对该理论提出了一种新的定义,由于引起偏应变和体应变的机制不同,因此采用不同的内蕴时间来度量,各向同性情况下有:

式中:μ0和K分别代表剪切弹性模量和体积弹性模量,k0,k1是系数,当k0=k1=1时,dηij,dθ分别为塑性偏应变分量与塑性体应变分量的增量,dζD为塑性应变空间的欧几里得模型,dζH是塑性体积应变的绝对值。ζ为广义内蕴时间量度,它通过一些反映材料性质变化及耦合效应的函数Rij以最后确定内蕴时间标度ZD和ZH。Rij是ζD和ζH以及其率的函数,R01和R10表示偏斜响应与体积响应的耦合效应。
当用于各向异性耗散材料时,内蕴时间量度ζD,ζH可统一表达为:

此时的内蕴时间标度表达为:

Qijkl(Z)是Z的函数,,为不可逆应变增量。于是,由本构方程形式不变性,并仿照线性粘弹性本构关系,可得到各向同性情况下的本构方程为:

μ (ZD),K (ZH)分别为偏量张量空间和球量张量空间的核函数,且其初值μ0=μ(0),K0=K(0)分别为初始剪切弹性模量和初始体积弹性模量,Sij为偏应力张量,eij为偏应变张量,σkk为体积应力,εkk为体积应变。
而各向异性情况下的本构方程可根据粘弹性力学基本公式表达为:

内蕴时间理论是以不可逆热力学为基础,理论基础比较深厚,优点是摆脱了屈服面的约束,在实际问题的计算中能用一个统一的公式描述全过程。根据本构方程形式不变性定律可利用已有理论的公式形式来给出本构方程,现在常用的是粘弹性公式形式,但并不局限于粘弹性公式形式。
内蕴时间理论是模仿Biot的线性粘弹性理论建立在Onsager不可逆热力学的基础之上,Onsager原理只在偏离平衡态不远时才能适用,对于有限弹塑性变形,内蕴时间理论的适用性还需进一步讨论。它对已知实验的解释程度,如何确定反映物质响应的积分核函数及物质所特有的内蕴时间,如何向大变形、大温度方向推广,以及如何进行有效的数值计算等问题,都需进一步研究。
最早把内蕴时间理论用于混凝土的是Bazant,Bazant的理论不涉及不可逆热力学,而是直接采用内蕴时间的概念,用试凑法和参数优化法得到参数值,他的模型能较好地模拟混凝土的性能,但是模型参数过多,而且一些参数有耦联关系,一些参数缺乏物理意义,使用起来过于繁琐。
1.4 断裂力学本构模型
为正确地反映混凝土内部裂缝的开展规律,正确选择一个建立在断裂力学理论上的开裂模型是至关重要的。严格来说,断裂力学不是一种材料的本构模型,但是断裂理论与应力-应变空间弹塑性理论的组合弹塑性断裂本构模型在预测一些典型的混凝土结构工作性能和强度方面发挥了重要作用。
断裂力学基本理论基于脆性材料假定建立Griffith断裂准则,并根据裂缝尖端应力和位移以确定该裂缝是继续扩展还是闭合。如果裂缝周围的材料不存在应力残余,则认为该材料是线弹性的,可以采用线弹性断裂力学以描述裂缝和材料的变形。然而,裂缝周围区域材料往往会发生比较明显的塑性变形,此时线弹性断裂力学理论不适用。为此,学者们提出了非线性断裂力学。目前,尽管大范围屈服或非线性断裂力学方法已经得到有力的开发和应用,但线弹性断裂力学由于应用简便、预测结果偏于保守的特点,仍在实际中有着广泛的应用。1961年,Kaplan首先将断裂力学引入混凝土中,其主要研究带裂缝的混凝土体的强度和裂缝的传播规律,从力学侧面研究宏观的断裂现象,包括宏观裂缝的形成、扩展、失稳开裂、传播以及止裂等。它着眼于混凝土体裂缝前缘附近的位移场、应力场、能量释放率G来研究带裂缝的构件强度、刚度和稳定性,分析裂缝扩展稳定性、扩展规律性,以建立宏观裂缝起裂、裂纹的稳定扩展和失稳扩展的判据,判断裂缝是否稳定,进而探讨如何控制和防止结构断裂破坏的措施。
Y.Zaitsev和Nemat-Nasser等结合局部平均概念,在局部意义上利用断裂力学基本理论对混凝土材料进行了分析,其结果表明,对于混凝土、岩石等准脆性材料,断裂力学模型能够给出可以接受的结果。
但由于混凝土材料的微裂缝在受荷之前即存在,而且其大小、方向、出现的位置及裂缝分布具有随机性;只有当裂缝尖端前的材料中存在均匀应力场时,断裂力学理论才能应用于裂缝的演化分析,然而,在混凝土材料中上述情况几乎不可能存在;在有限元分析过程中,每一荷载增量步甚至迭代步中的裂缝扩展都需要改变网格拓扑并重新划分网格,这些因素大大限制了断裂力学理论在结构分析中的应用。
1.5 损伤力学本构模型
工程结构或构件在荷载(如静载或动载)和环境(如温度、氧化、腐蚀等)作用下力学性能渐进劣化,这个过程即为损伤积累的过程。在微观上体现为内部微缺陷、微裂纹的形成及进一步发展,从而导致材料中宏观裂缝的出现,并使结构构件最终失效。以连续介质力学与不可逆热力学为基础的连续介质损伤力学把连续介质的微缺陷理解为连续的“损伤场”变量,并假定损伤的能量耗散过程满足不可逆热力学定律,利用连续介质力学的“唯象学”方法研究微缺陷(损伤)的发展及其对材料力学性质的影响。损伤理论的研究重点是:定义合理的损伤变量;建立材料损伤本构方程;探讨损伤的演化规律;寻求测量损伤程度的方法;预估结构或构件的剩余寿命。
损伤理论的研究始于1958年Kachanov提出“连续性因子”的概念来描述金属的蠕变断裂。由于该模型简单直观、物理意义明确,此后的众多损伤模型都在不同程度上借鉴了他的损伤理论思想。1963年Rabotnov又引入了“损伤因子”的概念研究金属的蠕变本构方程,建立了损伤理论的雏形。在受损材料中,从细观上对缺陷形式和损伤机制进行分析以确定有效面积是很困难的,为间接测定损伤,1971年Lemaitre提出了应变等价原理,并引入了有效应力的概念,成为将损伤变量引入材料应力-应变本构方程的桥梁。1977年Janson和Hult首次提出了“连续介质损伤力学”的概念,从此损伤力学在各国学者的努力下迅速发展,其中Lemaitre、Chaboche、Janson、Hult、Leckie-Hayhurst、Krajicinovic、Sidoroff、村上澄男等学者的研究工作为损伤理论的形成和发展作出了重要的贡献。与此平行,Rice-Tracey、Gurson等学者从材料细观结构出发,研究材料细观结构变化的物理与力学过程,发展了材料细观损伤力学。
在混凝土的损伤研究和实践中,大量学者针对具体工程情况提出了各种不同的损伤本构模型,但是由于适用条件的特殊性及所建立模型的复杂化,很少有一种能够有明确的物理意义、简单的表达、便于工程师接受的一般损伤本构关系式。基于对损伤本构模型的思考,作者试图以已有研究为基础,致力于建立能够反映混凝土破坏机理的一般损伤本构模型。
上述各种混凝土材料本构模型及其相互之间的交叉关系如下图所示。
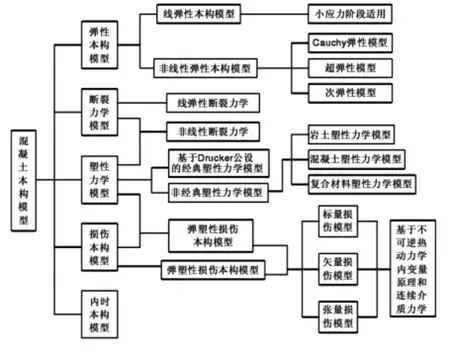
图1 混凝土材料本构模型交叉关系图
2 有关混凝土本构关系的展望
在混凝土的非线性有线元分析中,需要精度足够而又计算方便的本构关系表达式,这一直是众多研究者们重视的课题之一,这方面虽然已经有了很大的进展,但需要研究的问题仍然还有很多。可以预见今后对混凝土本构关系的研究,会在多层次、多角度进行。从实用分析的角度看,非线弹性模型、弹塑性模型已日趋成熟,并易于同通用的有限元程序匹配,因而还会更广泛的推广和应用,并有希望编入有关结构设计的规范中去,但在确定参数、改善精度方面还有相当的研究工作要做。为了适应混凝土的复杂加载和破坏的特点,将多种模式组合,如塑性断裂、粘弹塑性、塑性损伤、内时塑性、内时损伤等这些交叉理论将会得到进一步研究。此外,有关动力分析的本构关系,基于随机因素的本构关系值得进一步的探讨。从试验研究来看,在三向应力状态下的应力应变测得的数据还不够多。试验方法也有待改进,特别是在不改变受力与变形条件的现代非机械、非破损的测量方法还期待有所突破。从破坏机理来看,断裂力学、损伤力学的应用研究有很好的前景。这些理论结合微观的观察与分析来进行的研究,会在未来的十年中得到很大的发展。

